基于大规模数据的公交到站时间预测方法比较

庞俊彪，胡安静 ，黄 晶，杜 勇，于海涛

(1.北京工业大学 信息学部 北京多媒体与智能软件技术重点实验室，北京 100124；2.北京市交通信息中心，北京 100161)

0 引 言

交通在现代社会中扮演重要的角色，基于联合国人口署公布的报告：城市人口的增长率每年以大约1.5%的比例增长，预计在2050年，有大约64亿城市居住人口[1]。城市人口的增长将引发总出行需求的增长，就有限的交通资源来说，高效的公交系统既有利于降低城市交通拥堵，提高城市交通运转效率，同时也能减少汽车尾气排放，提升城市空气质量。在我国人口数量多、密度高，城市土地资源紧张，在城市化进程加快的过程中，优先发展城市公共交通是一项利于城市可持续发展的重要任务[2]。

考虑到发展公共交通带来的益处，城市公共交通管理部门希望引进相关的技术向乘客提供一些公交信息，从而提高交通服务水平[3]。在美国，有研究人员针对乘客所关心的公交信息种类进行问卷调查[4]：在众多的公交信息中，最让人关心的信息之一即为公交车到站时间。所以，准确预测公交车到站时间并及时将信息传递给用户，是提高服务水平的关键性一步[5]。准确的到站时间预测，可以有效减少用户的等待时间，提高服务质量[6]，方便和鼓励用户使用公共交通出行。正因为公交到站时间预测的重要性，使其成为一项重要的研究课题[7]。

在现实生活中，由于交通运输的随机性，如路口的延时、用户在时间和空间上需求的波动、天气情况等因素，公交到站时间很难进行预测。早年间，大多数公交车到站时间预测的研究，主要是通过大量调查，着重于预测模型的建立[8-9]。直到1999年，基于自动车辆定位技术(automatic vehicle location，AVL)的全球定位系统(global position system，GPS)的出现，使研究发生了质的飞跃[10-11]。随后，简单的线性预测模型被非线性预测模型取代，例如核函数机[12]、神经网络[13]等。然而正如O’Sullivan在文献[14]中关于公交到站时间预测不确定性的讨论所提到的：“公交到站时间预测问题的复杂性在于，公交运行时间是非线性和复杂的多种因素交互作用的结果。”

1 现有方法

回顾现有的大多数预测算法，公交到站时间预测算法根据原理的不同，大体可以分为三大类：基于回归算法、基于滤波算法、基于搜索算法。

1.1 基于回归算法

在基于回归算法中，将公交到站时间作为受其他时空因素控制函数的响应量。因此这类算法之间最大的差异在于，如何定义到站时间和其他时空因素之间的非线性关系。该类算法包括以下四种：

(1)SPB[8](SVM on probe buses)算法中首先将路径划分成路段，随后从运行在下游路段的前一辆公交作为探针，提出了四种特征作为模型的输入。支持向量机和支持向量回归的非线性，从数学本质上来说都来源于核函数。但确定核函数及其相应参数较为困难，计算复杂度大，不适用于解决大规模计算量问题[15]。实验中通过公开的源代码实现SVM算法。

(2)LRT[16](linear regression on trajectories)算法假设公交行进时间服从多元高斯分布，故而预计到站时间为公交到达目标站点的后验期望。

(3)AMM[17](additive mixed model)算法使用半参数模型来建立多因素模型，使用周末与否、当前时间、行进距离等因素，用函数来描述这些因素与公交到站时间之间的关系。文中利用R语言的MGCV包实现了AMM算法。

(4)MLP[18](multilayer perceptron)算法中使用了三种特征：当前时间、当前位置、与目标站点之间的距离。多层感知机是一种特殊的前向传播神经网络算法[19]，在本次实现中遵循原文的设计，选择和调整隐含层节点个数，报告节点数为15时得到的最好结果。文中使用MATLAB中的newff函数实现该算法。

1.2 基于滤波算法

遵循经典贝叶斯预测原理，基于滤波算法根据预先提供的路段信息，预测给定路段的行程时间，从而实现公交到站时间的预测。通过定义或者利用相应的模型学习公交车运行的动力系统，以递归的方式进行公交车到站时间预测。

卡尔曼滤波器是这类模型的典型代表。它是现代控制领域的一种重要方法，通过一系列的递归数学公式，即状态方程和观测方程组成的线性随机系统来描述，它是一种最优化自回归数据处理算法，采用线性无偏最小均方误差估计准则，对过程的状态进行预测。

KFP[20](Kalman filter with probe buses)算法首先将路径划分为路段，而后学习动态滤波器。实现过程中使用期望最大化实现线性动态滤波。

1.3 基于搜索算法

影响交通的因素众多，而这一类模型采取了“用替换代替预测”的策略来避免考虑这些因素。简单地假定在相似的交通环境下，公交车到达各个站点的时间是接近的。这种方法一般会以当前车辆的通行时间作为依据，去搜索一些相似的历史数据。

基于搜索算法在所预测公交运行的交通状况与历史数据相似的情况下，预测结果较好。为了提高准确率，将一天的时间按照定义的时间块进行分层[21]。但当处理大数量轨迹数据时，k-NN的计算复杂度将会很大。

k-NN[20]算法和KR[16](kernel regression)算法均是基于搜索的算法，通过权值化历史相似运营轨迹进行预测。如k-NN算法选择k条和当前轨迹最接近的历史轨迹，获得这些历史轨迹到达下游待预测站点的时间，并分别乘以权值(如1/K)得到当前公交车到达下游站点的时间。KR为了达到非线性[16]，采用基于核函数(如高斯核，exp(-‖x-y‖2/b))计算权值的方法，其中x和y代表当前的运营轨迹和历史运营轨迹，b是核的带宽。实验中根据文中的最优参数设置，设b=1。

1.4 讨 论

虽然现有很多算法，但因为数据获取较为困难，导致大多数算法并没有使用大规模的数据集对其进行验证，只使用极少的线路对算法进行性能评价，所以无法比较算法的准确性。并且在不同的数据集上进行的实验无法公平地比较各算法的性能，每种算法在不同的条件下会有不同的结果，比如某算法可能在短距离上的预测比较差，但在长距离的预测上却表现较好，所以各种算法缺少在同一数据集上进行对比。

2 大规模公交运营数据集的构建

目前，针对公交车到站预测问题，尚没有公认的大规模数据集，故文中选择了北京47条公交线路进行数据采集和预处理，并建立了北京市公交运营数据集。这些运营线路在北京市的分布如图1所示，其中黑色线条表示公交车的路径轨迹，它们几乎覆盖了北京市城区的主要干道。

将该数据集和其他研究所用到的数据集在线路数量、线路长度、站点数量等方面进行了比较，如表1所示，说明了数据集的无偏性和全面性。

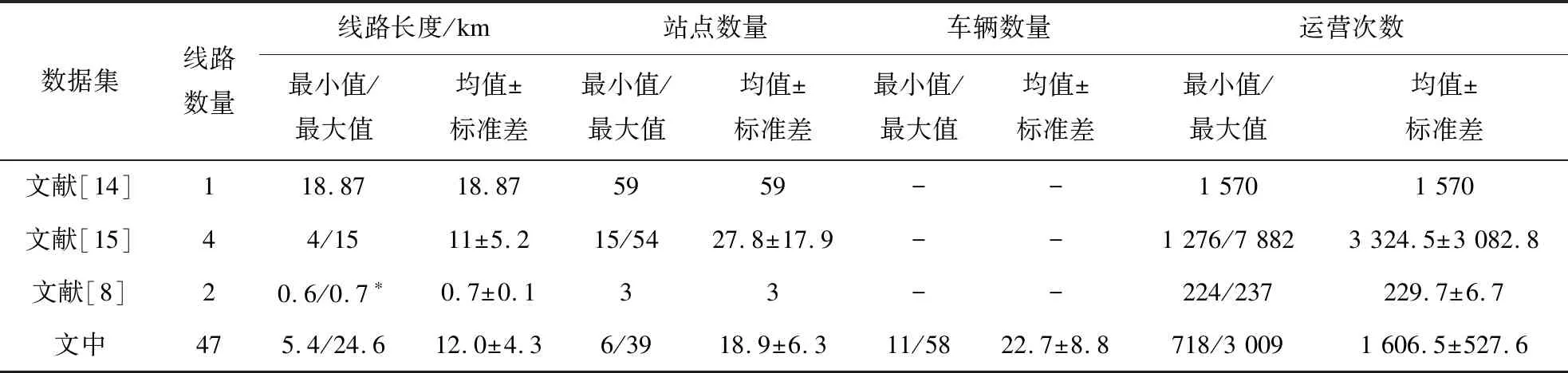
数据集线路数量线路长度/km站点数量车辆数量运营次数最小值/最大值均值±标准差最小值/最大值均值±标准差最小值/最大值均值±标准差最小值/最大值均值±标准差文献[14]118.8718.875959--1 5701 570文献[15]44/1511±5.215/5427.8±17.9--1 276/7 8823 324.5±3 082.8文献[8]20.6/0.7∗0.7±0.133--224/237229.7±6.7文中475.4/24.612.0±4.36/3918.9±6.311/5822.7±8.8718/3 0091 606.5±527.6

注：文献[8]只使用了两条线路的部分只含有3个站台的区间，作为个案研究，所以线路长度相对较短。

2.1 公交运营数据描述

数据集共两部分：公交的动态GPS数据；道路网的静态信息，如公交站台的位置，路口的位置，每个公交站台的相关统计量。

公交动态GPS数据从北京的47条线路，共1 089辆公交车中收集，数据时间跨度为2015年2月1号至2015年2月28号。每条GPS数据包括以下信息：公交车的经纬度坐标，时间戳，公交号，线路号。每30 s产生一条GPS数据，且最大位置误差为50 m。但由于高层建筑或天桥造成的信号传输的阻塞，GPS数据中存在误差数据。因此通过建立城市的边界，过滤这种错误的GPS数据，实验中设置经度范围为110～200，纬度范围为30～50，作为北京市的边界。

道路网的静态信息包括：公交站台的位置，线路号，行车方向，路口位置，公交站台的规模(每个站台有多少种线路的公交停靠)。其中路口预示有时间延后的可能性，公交站台的规模间接提供了公交在该站台可能停驻的时长。

2.2 大规模公交运营数据集构建

将GPS数据和静态信息数据协同映射为“到达时间-行驶距离数据对”。通过计算两个连续GPS数据点之间的距离，首先累积两点之间的距离，得到了行进距离。接着需要解决以下两个问题：将每个公交站台映射到行进距离中；获得每个站台的到达时间。

为了解决这两个问题，将每个站点的GPS坐标映射到行进距离中，通过插值得到相应的到达时间。

这一步骤中通过克里金插值法(Kriging interpolation)[21]的泛化算法，高斯过程(Gaussian process)[16]，得到插值点。由此，GPS数据和站点位置最终转化为一个时间空间联合的轨迹。

3 实 验

3.1 评估量设置

为了公平地评估每种算法的总体性能，使用平均绝对误差(mean absolute error，MAE)、均方根误差(root mean square error，RMSE)以及平均绝对百分比(mean absolute percentage error，MAPE)来评价预测精度，具体公式如下：

(3)

其中，i表示该线路的第i次运营；N表示运营的总量；K表示该线路站点的数量。

3.2 结果与讨论

分别用上述七种算法在测试集上进行实验对比。将47条线路按运营距离分为三类，分别为短距离(0～10 km)、中距离(10～15 km)和长距离(>15 km)，计算各线路的MAE、RMSE、MAPE。表2记录了三种评价指标在各组的均值和标准差。

表2 现有算法在本数据集上实现结果的比较

根据表2可知，KFP算法的总体性能最低，主要原因是KFP作为一种基于滤波算法，在预测时间时，只依靠下一步准确的测量对预测模型进行“纠正”。如果从历史数据学习到的动力系统和现实的交通情况出入较大，结果会迅速变差，并且不断累积和传播。

k-NN和KR算法在各种情况和各种指标下的表现很相近，正如所预期的那样，基于搜索的算法只有在当前的交通环境和搜索到的历史轨迹所对应的交通环境相似时才能预测较为准确的结果。

值得注意的回归类算法，如LRT和AMM都取得了较好的结果，因为这些方法避免了多步超前预测的难点，不需要迭代进行预测。其中LRT并不像k-NN和KR算法，只统计了历史相似轨迹，它捕获了公交不同路段之间运行状态的线性叠加关系，故而在大量数据的情况下，预测效果最好。

AMM是半参数回归模型的一种。该算法考虑多种因素，通过函数来描述因素和到站时间之间的关系，是一个统计型原理模型建立框架，灵活地整合了多种因素，算法总体性能较好。

SPB由于其预测结果与支持向量机中核函数及其参数的选择关系较大，所以参数较难控制，且SPB算法使用下游前一辆公交作为探针，所以对于前一辆公交的信息较为依赖，在某些情况下结果较差。

MLP算法的核心是典型的多层感知机网络，这是一种具有三层(输入层、隐藏层和输出层)神经元的前向型神经网络，文中使用了三种特征，分别为当前时刻，当前位置和目标站点之间的距离，输入特征较少，没有考虑时序间的关联性。

此外，由于交通的复杂性，预测其在较远时空下的状态相对较难，还将考虑在不同预测距离的情况下，算法的预测能力是否会有较大的变化。将预测距离划分为2 km一段，即[0,2)，[2,4)，[4,6)……通过图2来描述绝对误差在不同预测距离区间内的分布。

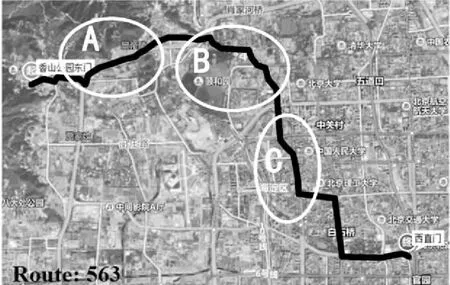
图2 线路563的分布

为了清晰地比较几种算法的误差分布，利用最长的563路公交线路对上述7种算法进行测试，如图2所示。该线路具有29个站点，且线路穿过了旅游胜地(香山)，著名的历史景点(颐和园)，集中商业区(中关村)，分别对应图2中A区域、B区域、C区域，通常拥有较大客流量，线路总体路况复杂，对于预测公交到站时间来说，具有挑战性，适合进行算法性能的比较。实验结果如图3所示，其中图中折线为第95个百分位的绝对误差。

从图3可以看出，各算法性能大致与表2中相同，但随着到达站台距离起点站台的距离逐渐增加，预测到站时间的绝对误差随之增加。值得注意的是，由于SPB算法是通过多条线路来预测公交到站时间，所以在只使用一条线路时，SPB算法性能最差也是预料之中的。

4 结束语

文中提供了一个大规模公交运营数据集，包括不同运营距离的线路，几乎覆盖了北京市城区的主要干道。与其他研究所用到的数据集进行了比较，表明该数据集有无偏性、全面性以及大规模等特点，为公平地比较现有算法提供了可靠准确的数据基础。在将各算法按照原设计实现后，在该数据集上进行实验对比，发现基于回归算法的各方法具有更稳定的性能。且各方法在不同长度线路上的结果中LRT算法的结果最好且稳定。

随着线路的行进，公交到站时间预测的准确性越来越差，从绝对误差看出预测到站时间越来越不准确。所以从预测准确度的角度看，到站预测算法还有很大的研究空间。尤其是如何融合多种异构信息进行预测，目前只能关联时间、空间两种因素，而对于路况、道路约束、天气等因素无法进行建模和利用。这也将是到站时间预测未来努力的方向之一。