随机分形搜索算法
葛钱星,马 良,刘 勇
(上海理工大学,上海 200093)
0 引 言
近年来,元启发式算法取得了巨大的发展,出现了许多有代表性的方法。例如,遗传算法(genetic algorithm,GA)是基于生物进化论中“自然选择、适者生存”规律而提出的优化方法;粒子群优化算法(particle swarm optimization,PSO)是基于鸟群觅食行为规律而提出的群体智能优化方法[1];人工蜂群算法(artificial bee colony,ABC)是基于蜜蜂群觅食行为特性而提出的优化方法[2];蚁群算法(ant colony,AC)是基于蚁群在觅食过程中的行为特性而提出的仿生类算法[3];引力搜索算法(gravitational search,GSA)是基于万有引力定律而提出的智能优化算法[4-5];布谷鸟搜索算法(cuckoo search,CS)是基于布谷鸟的寄生育雏的行为特性而提出的元启发式算法[6-7]。这些方法有助于许多复杂困难优化问题的求解[8-15]。但是,随着所研究的优化问题越来越复杂,具有大规模、不可微、非线性、不确定性、多目标等特征,这些算法也相继暴露出一些固有的缺陷,如易陷入局部极值和收敛速度慢等。因此,设计新型的优化算法仍然是值得关注的研究方向。
伊朗德黑兰大学学者Hamid Salimi于2015年提出了随机分形搜索算法(stochastic fractal search ,SFS)[16],该算法是基于分形的扩散性质进行优化搜索。其基本原理是,引入分形的扩散过程作为其搜索机制,并选择高斯分布作为扩散过程的随机游走方式。然后,根据各个体的适应度函数值进行选择,并对各个个体的分量和位置进行更新,最终求得问题的最优解。
Hamid Salimi利用随机分形搜索算法对一系列标准无约束函数优化问题进行数值实验,并与回溯搜索优化算法、差分进化算法和引力搜索算法等进行比较,实验结果表明,该算法具有较高的计算精度和较快的收敛速度。此外,还利用随机分形搜索算法求解了部分工程设计优化问题,包括弹簧设计问题、压力容器设计问题和焊接梁设计问题等,并与遗传算法、共同进化粒子群优化算法、共同进化差分进化算法等进行比较。实验结果同样表明,随机分形搜索算法具有较好的优化性能。
1 随机分形
随机分形是一种常见的分形,它们的生成具有很大的随机性,没有确定的数学法则,其自相似性不是表现在形态上,而是表现在结构或复杂度上,这种相似性是近似的,具有统计意义上的自相似性。因此,又称为统计分形[17]。
随机分形可以通过随机规则来产生,如莱维飞行,高斯游走,渗透集群,自回避行走,分形景观,布朗运动和布朗树的轨迹(即通过模拟受限扩散凝聚或受限反应聚集簇产生的树枝状分形)[18]。一些随机分形,例如描述细菌菌落的簇,可以通过称为“受限扩散凝聚”(diffusion limited aggregation,DLA)的物理模型而生成[19]。为简单起见,考虑在平面上形成这样的簇,初始(种子)粒子位于原点。随后在原点附近产生其他粒子,从而引起扩散。为了模拟扩散过程,采用了随机游走的数学算法。扩散产生的粒子粘附在种子粒子上并重复该过程直到形成簇。在形成簇时,与穿透内部的粒子相比,扩散产生的粒子粘附于簇上的概率增加。因此,这种性质会导致所形成的簇呈分支状结构,如图1所示。
2 随机分形搜索算法
受随机分形扩散性质的启发所提出的随机分形搜索算法,主要包括扩散过程和更新过程。在扩散过程中,每个个体围绕其当前位置进行扩散,从而增加了找到全局最优值的机会,并且可以防止陷入局部最优值。另外,在随机分形搜索中,来自扩散过程的最佳生成个体是唯一被保留的个体,剩下的个体均被丢弃,这样就有效地避免了因扩散过程导致个体数量急剧增加;在更新过程中,群体中一个个体的位置的更新是根据其他个体的位置来进行的。

图1 通过受限扩散凝聚方法产生的一种简单分形
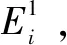
为了在扩散过程中产生新的个体,文献[16]研究了莱维飞行和高斯分布两种统计方法[20]。对莱维飞行和高斯分布的初步研究显示,尽管莱维飞行在几代中收敛速度高于高斯游走,但高斯游走比莱维飞行更有希望找到全局最优解。因此,选择高斯分布作为随机分形搜索的扩散过程中唯一的随机游走方式。通常,参与扩散过程的一系列高斯游走如下所示:
GW1=Gaussian(μBP,σ)+(ε×BP-ε'×Pi)(1)
GW2=Gaussian(μP,σ)
(2)
其中,ε和ε'是在区间[0,1]上服从均匀分布的随机数;BP和Pi分别表示群体中的最佳个体和第i个个体的位置。式1中两个高斯参数是μBP和σ,其中μBP正好等于|BP|;式2中两个高斯参数是μP和σ,其中μP等于|Pi|。高斯参数中的标准差σ为:
(3)

Pj=LB+ε×(UB-LB)
(4)
其中,LB和UB分别是求解问题的向量的上下边界;ε是在区间[0,1]上服从均匀分布的随机数。
在初始化所有个体之后,计算每个个体的适应度函数值以获得所有个体中的最佳个体(BP)。根据扩散过程的开发性质,所有个体都围绕着当前的位置游走以开发问题的搜索空间。另一方面,由于探索属性,考虑了两个旨在进行更好的空间探索的统计过程作为更新过程。第一次更新过程对每个个体的分量索引执行,然后将第二个统计方法应用于所有的个体。
对于第一次更新过程,首先根据适应度函数值对所有的个体进行排序,然后给种群中的每个个体i设置性能级别Pai,如下:

(5)
其中,rank(Pi)为个体Pi在种群中的排名;N为种群中个体的数量。
事实上,式5表明点越好,则其被选中的概率越高。该式用于在还未获得良好解决方案的情况下增加改变个体的位置的机会;另一方面,在下一代传递良好解决方案的机会将会增加。对于群体中的每个个体Pi,判定条件Pai<ε是否满足,若满足,则根据式6更新点Pi的第j个分量;否则,保持不变。
(6)


(7)
(8)

基于以上分析,随机分形搜索算法的主要步骤可描述如下:
Step1:设置参数,并初始化种群。
Step2:计算种群中每个个体Pi的适应度函数值,并找到最佳点BP。
Step3:执行扩散过程。对于每一个进行扩散的个体,根据所选择的高斯游走方式创建各个新个体的位置,并找到所有个体中的最佳个体,进行函数返回。


Step6:判定迭代次数G>最大迭代次数是否满足,若满足,则算法结束,处理并输出结果;否则,执行Step3。
3 仿真实验及其结果
为验证算法的可行性和有效性,采用CEC’2010标准测试函数库进行仿真实验,并与回溯搜索优化算法(backtracking search optimization,BSA)[21]、协方差矩阵自适应进化策略(covariance matrix adaptation evolution strategy,CMA-ES)[22]、差分进化算法(differential evolution,DE)[23]、引力搜索算法(gravitational search,GSA)[4-5]、人工蜂群算法(artificial bee colony,ABC)[2,24]、动物迁徙优化算法(animal migration optimization,AMO)[25]进行比较。
对于CEC’2010测试函数,统一设置维度为30。所有算法的种群规模统一设置为100,并且每种算法独立运行25次。对于随机分形搜索算法,最大扩散数量设置为q=1,其他几种算法的控制参数详见文献[2,4,21-22,25-26]。仿真结果如表1所示,可参考文献[27]查看函数详细信息。对于每个基准函数,表1给出了各个算法运行25次的平均解,并根据平均解从最低到最高对所有的算法进行排名,然后对这二十个函数的排名进行平均化处理,从而得到各算法的综合排名。


表1 不同算法求解CEC’2010基准函数的仿真结果比较

续表1

由表2中得到的结果表明,随机分形搜索算法中的每个过程都能显著影响最终结果的质量,并且随机分形搜索算法的所有过程共同形成了一个完整的系统来解决优化问题。此外,通过大量的实验表明,对于大多数的函数优化问题,当MDN (最大扩散数量)=1时,随机分形搜索算法通常可以找到问题的全局最优解。一般来说,根据所研究的问题调整MDN这一参数肯定是有益的,但是其重要性是相对而言的;另一方面,增加MDN会面临要进行时间消耗和收敛速度之间的权衡。

表2 三种搜索机制的仿真测试结果
4 结束语
随机分形搜索算法是一种在精度和时间消耗方面都很成功的新型元启发式算法。该算法基于分形的扩散特性进行优化搜索,为优化算法的设计提供了新思路。为验证算法性能,对CEC’2010基准函数进行了仿真实验,并与其他算法进行比较,实验结果表明该算法具有较好的可行性和有效性。基于算法良好的优化性能,其潜在的研究方向包括但不限于以下几点:
(1)算法的理论研究:当前对随机分形搜索算法的研究主要借助于数值实验,缺少严格的数学论证。因此,后续研究可以对此进行展开。针对收敛性的证明可以尝试利用马尔可夫链等进行推导。
(2)算法的设计研究:与大部分仿生智能优化算法不同,随机分形搜索算法是将分形扩散性质融入智能优化算法思想当中的新型算法。要充分吸收分形扩散的研究成果,从而更加有效地设计算法的搜索机制,进一步提高算法的优化性能。其次,还可以利用现有的优化算法,包括经典优化算法和智能优化算法,结合随机分形搜索算法提出改进的混合优化算法。此外,还可以考虑引入自适应策略进行参数控制等。
(3)算法的应用研究:基于算法良好的优化性能,其应用前景将十分广阔。目前,随机分形搜索算法已经用于求解机械零部件设计等问题,并且取得较好的结果。算法的应用范围还可以进一步推广,例如TSP问题、0-1背包问题和二次分配问题等组合优化问题以及路径规划、智能电网调度优化和应急选址等。

