基于时效规则的数据修复方法∗
段旭良,郭 兵,沈 艳,申云成,董祥千,张 洪
1(四川大学 计算机学院,四川 成都 610065)
2(成都信息工程大学 控制工程学院,四川 成都 610054)
3(四川农业大学 信息工程学院,四川 雅安 625014)
时效性是数据的重要属性,在数据挖掘、数据分析、数据增值应用中,准确的数据时效决定着诸如时间序列分析、关联、推荐等一系列算法的效果.相关学者采用直接观测、社会调查、理论推导等方式对数据质量问题展开研究,并分析得出对数据可用性影响较大的性质有:精确性、完整性、一致性、时效性和实体同一性[1].2002年有专家报告指出:在商业数据领域,由于客户信息的变化,每月有2%的商业数据陈旧过时[2,3].大量时效不精确的数据充斥在数据集中,如果不能识别哪些是最新的,数据查询可能会返回错误结果,数据分析可能产生相悖的结论,随之而来的是数据质量下降、数据价值降低.大数据时代,人们的各类数据非集中化地分布于各类平台和系统中,形成数据孤岛,数据时效不精确、数据过时带来的问题愈加严重.
不确定数据的产生原因很多,但总体可以归结为客观条件限制和人为故意两大因素:客观条件限制包括环境影响、采集设备精度限制、传输错误和意外事故导致的数据缺失或不精确;人为故意则是为了满足特定需求,如隐私保护等,对原始数据进行模糊化处理.针对数据修复工作的相关研究主要集中在数据不一致、不精确、不完整等问题上,研究者和工程技术人员提出了一系列针对这些问题的数据修复方法.从20世纪80年代开始,针对不确定性数据的概率数据库(probabilistic database)相关研究一直在进行,这类研究工作将不确定性引入到关系数据模型中去,研究领域涵盖了模型定义、预处理与集成、存储与索引、查询与分析等基础和应用研究的各个方面[4,5].针对不完全、不确定数据查询的研究较早地涉及到时效缺失或者时效不精确等问题,包括时态数据库模型构建、相关查询语言定义与分析等[6,7].
大数据和人工智能时代,个人大数据蕴藏着不可估量的社会和经济价值,个人数据银行模式是一种有效整理整合个人数据、提高个人数据质量和价值、增强个人数据可控性和可用性、有效保护个人数据隐私的新模式[8].在数据汇聚过程中,由于个人数据的分散度高、可管理性差,面临着更多的冗余和数据不一致问题,数据质量也难以保证,很大程度上影响着数据银行模式的健康发展.同时,个人数据又是一种典型的动态数据,反映个人属性、状态的各项数据是不断动态变化的,这个特性也是个人数据清洗过程中面临的最大挑战.在数据银行模式下,为了保证数据质量、提高数据价值,需要汇聚来源众多的数据,其时间属性往往是不精确的[9].对数据某些属性来说,不同时间对应不同值或状态,如一个人的学历变化、婚姻状况变化等,如果时间戳不完整或不精确,无法判定记录先后关系,会给数据增值应用带来极大的困难.
当前,国内外针对数据时效性修复的相关文献总体较少,专门应用到数据时效恢复的方法不多,大致可以分为两种:基于语义规则的方法和基于统计的方法.基于语义规则的方法根据领域专家知识或函数依赖、条件依赖、时效依赖,发现数据错误进行修复[10,11];基于统计的方法通过分析数据规律,如可能世界模型及概率数据库等相关方法,目的是寻求最大正确可能的修复策略[5,12].
虽然数据时效性问题面临的形势非常严峻,但并不是毫无希望.2011年前后,Fan等人提出了基于数据语义信息推断数据缺失值的数据时效性修复问题,在同一个实体具有多个元组的假设下,对数据时效性模型(a model for data currency)、数据时效性推理(reasoning about data currency)、时效性复制(currency preserving copy functions)等领域问题进行了深入研究,对相关概念进行了形式化的描述及定义,将这一领域的基础理论研究向前推进了一大步[13,14].在此工作的基础上,又有一系列卓有成效的研究在理论和实践上推动了数据时效性修复相关研究进展.文献[10]基于数据时效和数据一致性解决同一实体不同元组属性不一致的情况,提出采用数据的局部时效顺序表示数据的可用时间信息,在数据中提取时效约束条件表示数据时效关系,根据常量条件函数依赖确定数据的最新值.文献[15]研究了包含冗余记录的集合在给定时效约束下的时效性判定问题,提出了时效性判定问题的求解算法;文献[16]研究了规则和统计相结合的过时数据修复方法,既能够以传统规则的方式表达领域知识,又可以使用其特有的分布表来描述数据随时间变化的统计信息;文献[17]提出了一种结合质量规则和统计技术的提高数据时效性的修复方法;文献[18,19]提出在动态数据集上通过构建实体查询 B-树和实体存储静态/动态链接列表提高数据时效性确定效率和加速数据时效更新,提高了在大数据集上时效处理效率.
数据时间戳的恢复是研究的一个难点,如果数据时间戳缺失,是很难进行精确修复的;而根据一些规则,还原数据先后关系,确定缺失时间戳的区间范围,是一种可行、有效的策略.文献[20]提出了采用时序约束修复数据时间戳的方法,采用最小化修改原则使事件满足时序约束条件,一方面可以恢复缺失时间戳事件的所在时间范围;另一方面,也可以用于异常发现,对违背时间约束的事件进行检测和修复.实际上,在大多数数据分析和应用中,对数据先后关系的依赖相对于精确的时间显得更为重要,如广泛应用的时间序列、关联、推荐等一系列算法,基本都是以数据顺序作为基础实现相关功能.因此,对缺失时间戳数据的时间顺序进行修复既可以满足大多数分析应用对顺序的要求,又可以确定记录的新旧满足时效性查询需求,有利于数据质量和数据价值的提升.
数据时效性是决定数据质量的关键因素之一,本文主要研究时间戳缺失或者不精确的情况下,同一实体不同属性值的时序修复问题,在之前学者研究的基础上,重点针对“时序”即记录时间顺序开展研究工作.第 1节进一步明确时效规则的形式化定义,分类和定义值类型时效规则、状态类型时效规则,并对时效规则的支持度进行了定义.第2节提出状态类型时效规则提取和数据修复算法,并以实际算例展示算法过程和原理.第3节为实验结果与分析,在真实的数据集上验证规则和算法的效率和有效性,分析与讨论影响时效修复算法效率和正确率的相关因素.最后总结全文,并对未来值得关注的研究方向进行初步探讨.
1 时效规则概念和定义
本文定义的时效规则是指同一实体在不同时间阶段的数据记录在某些属性上随时间推移表现出的一些规律性特征.令关系数据库模式R=(EID,A1,…,An),其中,EID为实体标识符,具有相同EID的不同的元组对应同一实体(entity),EID可以由实体识别技术生成[21,22];Ai为第i个属性,其值域为dom(Ai).
定义1(属性的时效规则).对于关系R上同一数据实体的元组,某些属性依元组的时间顺序表现出递增、递减或服从特定的状态转换序列,我们称该属性满足时效规则.若属性Ai满足时效规则,参照Fan等人关于数据时序的定义,将其表示为
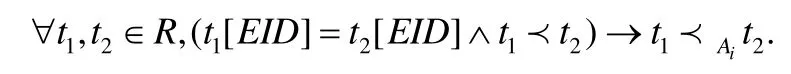
即:对于关系R中同一实体的元组t1,t2,如果t2比t1新,则元组t2的Ai属性比t1元组的新.
在此,我们假定数据是一致的,不违背函数依赖和条件依赖关系,即:不存在t1中的某一属性Ai比t2中的新,则以下关系依然成立:

即:对于同一实体的两个元组t1,t2,如果Ai满足时效规则,且t2的Ai属性值比t1新,则元组t2比t1新.
例如,年龄随时间递增,一个人的学位状态为学士、硕士、博士,婚姻状态为未婚、已婚、离婚等,则年龄、学历、婚姻状况等均满足时效规则.反过来,如果记录一个人的两条数据中学历状态分别为博士、硕士,则学历为博士的数据更加的新一些.
定义2(值类型时效规则).关系R上对于隶属于同一实体的两个元组t1,t2,如果某一数值属性Ai满足:

我们称Ai为值类型时效规则.反过来也成立:
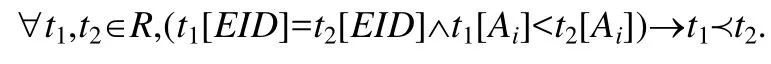
例如,人的年龄、一般情况下的薪酬都是随时间递增的.
定义3(状态型时效规则).关系R上,属性Ai的所有不重复值作为有限状态集合,表达属性时效规则的状态图是一个有向图G(V,E),其中,顶点集V表示属性值(状态)的有限集合,有向边集E表示随时间先后顺序状态迁移的方向.对于关系R上隶属于同一实体的两个元组t1,t2,其属性Ai的值分别为v1,v2,且v1,v2为图G的状态结点,若t2比t1新,则在状态图G中,v1到v2可达且v2到v1不可达,称v1→v2为一条状态型时效规则,表示如下:
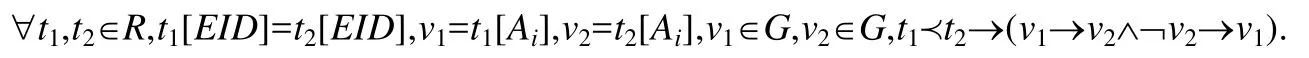
同理,在一致的数据集上:

如,学位状态或学生不同学期选课状态可用有向图如图1所示.
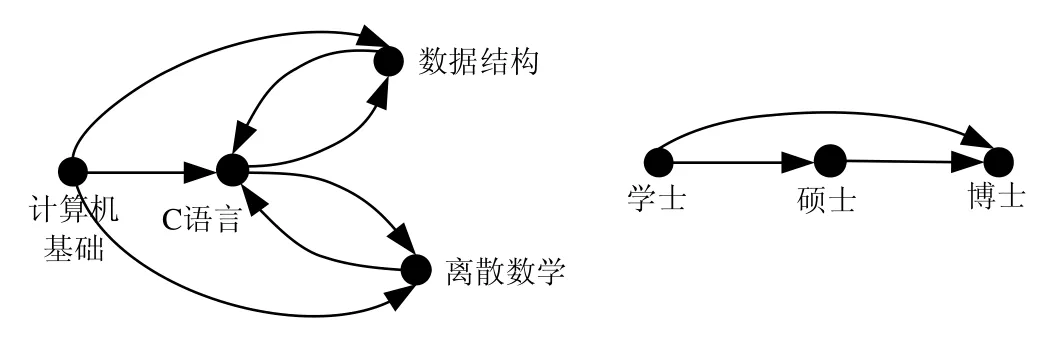
Fig.1 Directed graph of attribute state changing图1 表示属性状态变化的有向图
其中,如果两个状态之间无环,则这两个状态存在确定的时序关系,否则时序关系不确定;如在学位状态中,“本科”“硕士”“博士”存在先后关系;选课状态中,“C 语言”状态在“计算机基础”状态之后,而仅依靠“C 语言”“数据结构”或“C语言”“离散数学”无法确定先后顺序.一般地,考虑到数据记录的缺失,从无环规则起点状态到后续状态节点形成的路径依然是有时序关系的,如“学士”到“博士”、“计算机基础”到“数据结构”、“计算机基础”到“离散数学”等.
定义4(强时效规则).在一致的数据集上,如果所有实体上都满足某属性的一条时效规则,则称为强时效规则.如,没有某人的年龄会逐年递减.所有人的年龄都是随时间非递减的,就是一条强时效规则.
定义5(弱状态时效规则).在一致的数据集上,如果只有部分实体满足某属性的一条时效规则,则称为弱状态时效规则,用支持度来衡量该规则的强弱.实际上弱状态时效规则用支持度对状态型时效规则进行了扩充,若某条状态时效规则的支持度为1,则它是一条强时效规则,否则即为弱时效规则.
定义6(状态时效规则的支持度).在一致的数据集上,对于某属性的一条状态时效规则,满足该规则实体数与满足和违背该规则实体数之和的比值称为该时效规则的支持度,表示如下:
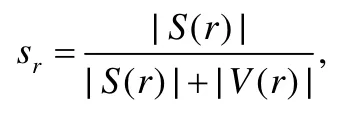
其中,sr表示规则r的支持度,S(r)表示满足规则r的实体集合,|S(r)|表示求集合中实体数量,V(r)表示违背该规则的实体集合,|V(r)|表示违背规则r的实体数量.
例如在选课状态图中,边的权值表示数据集中满足这条路径规则的实体数量,对于学生的选课规则“C语言→数据结构”,图2表示有99人先修“C语言”后修“数据结构”,有1人先修“数据结构”后修“C语言”,则“C语言→数据结构”这条规则的支持度为99/(99+1)×100%=99%.同理,“C语言→离散数学”这条规则的支持度为50%.
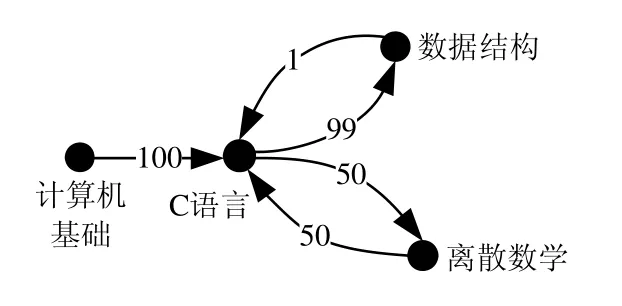
Fig.2 Calculation of rule support in a directed graph图2 有向图中规则支持度的计算
定义7(状态时效规则的强度).规则的强度直观上描述的是规则的重复次数越多,强度越高.需要说明的是:参见对支持度的定义,如果从某个状态节点v1到v2有且仅有一条有向边,但是v2到v1不可达,规则v1→v2的支持度依然为 100%,但这条规则可能是一个特殊的个例,重复性极低、代表性差,对数据时效修复价值不大.考虑到这种情况,引入了规则强度的概念,即规则的重复次数越多,强度越高.强度函数应根据数据实际特征进行定义.本文在实验测试中使用了Logistic函数作为强度函数.
2 时效规则提取及数据修复
2.1 状态时效规则提取
本文重点讨论状态类型时效规则识别.在一个数据集中,不同实体某些字段的状态转换是符合特定顺序的.根据在数据集中提取的状态时效规则,可实现对部分实体记录的缺失时序进行修复.在某属性的状态类型时效规则提取过程中,首先按时间顺序提取每个实体在该属性上的状态变化有向图,然后对图进行清理合并,计算图中存在关联关系状态转移的支持度.规则提取的结果可用有向图G(V,E)结构表达,结点集V表示有限的状态集合,有向边集E表示一条边连接的两个结点的状态转移方向,有向边的权值为两个状态转移支持度大小.
下面用实例说明状态类型时效规则提取方法和流程.
例1:状态类型时效规则提取.
首先用示例说明状态类型时效规则提取流程.设两个学生A,B选课序列按时间顺序排序后,分别为:
·A:计算机基础→C语言→数据结构→数据库;
·B:计算机基础→数据结构→C语言→数据库.
将课程作为状态,通过以下操作即可完成状态类型时效规则识别.
(1) 提取A的时效规则,分别为“计算机基础→C语言”“计算机基础→数据结构”“计算机基础→数据库”“C语言→数据结构”“C语言→数据库”“数据结构→数据库”;
(2) 提取B的时效规则,分别为“计算机基础→数据结构”“计算机基础→C语言”“计算机基础→数据库”“数据结构→C语言”“数据结构→数据库”“C语言→数据库”;
(3) 合并A,B规则,生成状态属性的有向图,如图3所示;
(4) 清理后状态属性有向图如图4所示,边的权值表示满足该时效规则的实体数;
(5) 计算规则支持度.根据定义6,计算所有规则的支持度.由图4可知:除规则“数据结构→C语言”“C语言→数据结构”支持度为50%外,其他所有规则支持度为100%.不难推算,假设学生C的选课序列和A一致,则“C语言→数据结构”支持度为66.7%,“数据结构→C语言”支持度为33.3%,其他规则支持度依然为100%.
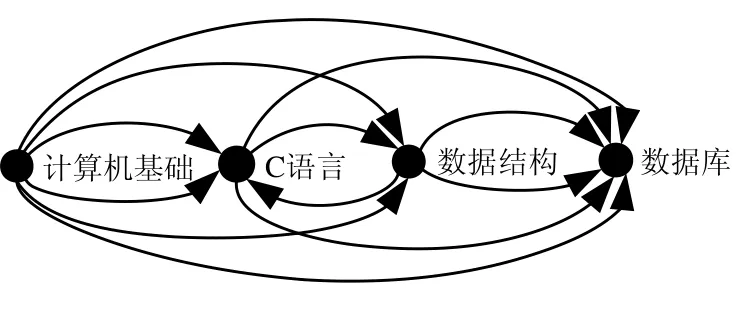
Fig.3 Directed graph of state attributes derived from data set图3 从数据中提取的属性状态有向图
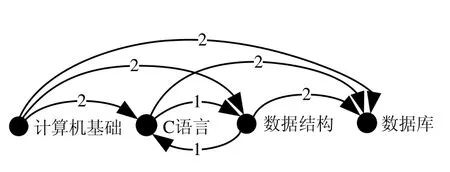
Fig.4 Calculating the weight of edges in directed graph图4 计算有向图中边的权值
需要说明的是:该算法支持动态增量数据集,当有新数据实体的记录加入时,可在原来基础上进行动态更新,不必在整个数据集上重新计算.由例1可见:当状态数比较多、规则比较复杂时会形成非常复杂的状态图,使用邻接矩阵表示会造成很大的存储开销.同时,查找路径、遍历图代价也很高.考虑到每条时效规则实际上就是连接两个状态节点的一条边,算法实现采用哈希表“键-值”(Hashtable,key-value)数据结构,以规则作为键,以满足该规则的实体数量作为值,实现规则的高效添加和检索.理论上,一个哈希表结构存储的“键-值”对可以是无限多个,但是检索的时间代价为常数复杂度O(1),回避了对复杂图结构的高代价遍历,可极大提升算法运行效率.状态类型时效规则提取算法详见算法1.
算法1.状态类型时效规则提取算法.
输入:已完成实体识别的、一致的、包含时序标签的数据集R;E为实体集,e为某个实体,e∈E,一个实体e对应数据集中n条记录;
输出:哈希表表示的“规则-规则支持度”集合.

2.2 基于规则的时序修复
时间作为一个连续值,一旦缺失,几乎没有办法被精确恢复.数据时效修复算法的目的是根据特定规则恢复同一实体记录间的时间顺序,根据时间顺序判断记录的早晚和某些属性值的新旧,满足数据分析处理应用和查询时效性需求.
例2和例3通过实例直观地展示了基于状态时效规则进行时序修复的原理和过程.
例2:数据时效修复实例.
下面用示例说明时效修复算法流程,我们已经通过例 1的学生A,B选课序列得到了全部规则及其支持度,见表1.
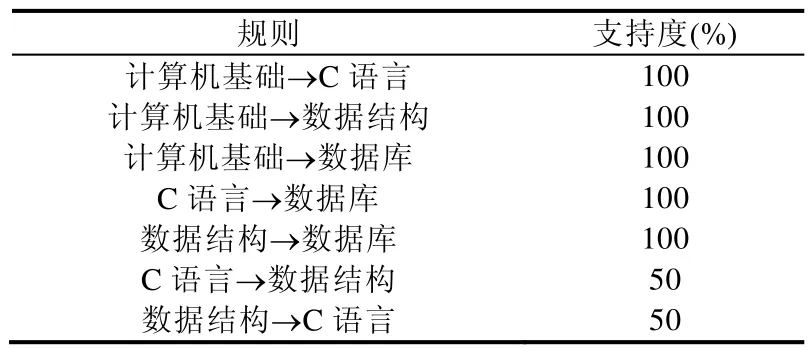
Table 1 Support of different rules in example 1表1 算例1中不同规则的支持度
假设已知学生C的选课序列:①计算机基础→②C语言→③数据结构,①~③表示数据记录时间索引,顺序排列;一门课“数据库”的时间属性缺失,下面要做的是通过时效规则匹配还原“数据库”这门课程在选课序列中的位置.
(1) 以“数据库”为起始结点穷举路径,得到“数据库→计算机基础”“数据库→C语言”“数据库→数据结构”;
(2) 以“数据库”为终止结点穷举路径,得到“计算机基础→数据库”“C语言→数据库”“数据结构→数据库”;
(3) 在“规则-支持度”哈希表中依次检查满足大于支持度(如要求支持度>60%)的步骤(1)中的规则是否存在:若存在,将规则后件时间索引添加到后继时序列表中.检查发现,“规则-支持度”哈希表中无步骤(1)中的规则,后继时序列表为空;
(4) 在“规则-支持度”哈希表中依次检查满足大于支持度(如要求支持度>60%)的步骤(2)中的规则是否存在:若存在,将规则前件时间索引添加到前驱时序列表中.检查发现:“计算机基础→数据库”“C 语言→数据库”“数据结构→数据库”均满足支持度要求(100%>60%),规则“计算机基础→数据库”的前件“计算机基础”时间索引为①,规则“C 语言→数据库”前件“C语言”时间索引为②,规则“数据结构→数据库”的前件“数据结构”时间索引为③,因此,前驱时序列表为{① ,②,③};
(5) 处理步骤(3)、步骤(4)生成的后继前驱时序列表,确定当前状态“数据库”时序.此例中,后继时序列表为空,可确定“数据库”状态结点出度0是图的一个终点,前驱时序列表为{① ,②,③ } ,因此可确定“数据库”时序索引为④,完成时效顺序恢复:①计算机基础→②C语言→③数据结构→④数据库.
例3:假设已知学生C的选课序列:①计算机基础→②C语言→③数据库,①~③表示数据记录时间索引,顺序排列;一门课“数据结构”的时间属性缺失,通过时效规则匹配还原“数据结构”这门课程在选课序列中的位置.
根据例 2的处理流程,可得“数据结构”的前驱时序列表为{①},后继时序列表为{③},可确定“数据结构”时序索引为②,但其与“②C 语言”先后关系不确定.修复后,各状态时序为:①计算机基础→{②C 语言,②数据结构}→③数据库.
但是如果假定“C语言→数据结构”支持度为66.7%,“数据结构→C语言”支持度为33.3%,其他规则不变,依然要求支持度>60%,则“数据结构”的前驱时序列表为{①,②},后继时序列表为{③},可通过插值确定“数据结构”时序索引,如2.5,修复后各状态时序为:①计算机基础→②C语言→③数据结构→④数据库.
算法2描述了对数据进行时效顺序修复算法原理和流程,其返回结果为补充了时序标签的记录集.
算法2.数据时效修复算法.
输入:哈希表表示的“规则-规则支持度”集合RuleSupportHash,完成实体识别的、一致的、包含时序标签的数据集R,待修复的缺失数据标签的记录集R′;
输出:补充了时序标签的记录集R″.


3 实验结果与分析
3.1 实验配置
实验硬件环境为Intel i3 2130 3.4GHz CPU,6G内存,操作系统为Windows10,所有算法均采用C#实现.
测试数据集为某高校教务系统选课数据,无异常数据,数据记录字段包括课程名、教学班编号、学号、学期等.必修课按培养方案一般安排在固定学期,具有较强的时序性,选修课则没有明确限制.但该高校在处理学生选课过程中较为灵活,学生可以根据自己情况选修本专业或其他专业必修、选修,也可提前选修本专业必修课,如某学生可能在大一选修大四某门必修课,在大二选修大三某门必修课,因此时效规则面临更多的不确定性,个别学生的随意选课也可视作噪声数据.根据实验需求分两部分.
(1) 数据集1为2014级8 626人的7个学期532 417条选课数据,平均每人60条选课记录,覆盖全校2 200多门课程,主要用于时效规则提取;
(2) 数据集2为2015级9 500人的5个学期472 962条选课数据,平均每人50条记录,主要用于时效修复测试.
数据预处理:在数据集中,选课时间形如“2017-2018-1”的字符串,表示2017-2018学年第1学期,为方便处理,针对每一个实体的全部记录,按选课学期升序排列,依次将选课学期处理为 1,2,3,…,7数值形式,“1”表示学生入校后第1学期,“2”表示学生入校后第2学期,依此类推.
算法针对每个学生每门课程选课学期的先后顺序提取时效规则,并进行时效修复实验.实验中提到的相关术语解释如下.
(1) 状态:指状态图中的状态结点.这里测试我们选取课程名作为状态,相同的课程名表示相同的图结点,不同的课程名表示不同的图结点.采用的测试数据中,总计有2 200多门课程,意味着状态图中最多有2 200多个结点;
(2) 实体:测试中的实体即学号.测试数据集中,一个实体对应多条数据记录,即:同一个学生有多条选课记录,学号相同的记录是同一个人的选课数据;
(3) 状态类型的时效规则,下文叙述中简称规则.对于实验数据集来说,规则可以解释为选课的先后顺序.
3.2 状态时效规则提取算法参数及效率分析
实验主要测试算法执行效率及影响算法效率的相关因素.时效规则生成需扫描数据集1中每个学生的7个学期选课记录,学生越多,扫描工作量越大,所以通过增加实体数量即可完成测试.实验依次随机选取数据集中的200,400,600,…,8000个实体,分别统计不同实体数量情况下状态数、规则数、支持度超过60%的规则数、支持度超过80%的规则数、支持度超过95%的规则数、规则扫描耗时、计算支持度消耗时间.
(1) 数据特征分析
实体数与状态数关系如图5所示.总体上看,状态数随实体数增加呈现对数增长趋势.开始阶段,随实体数增加,状态数迅速增加;当实体数增加到2 000左右时,状态数增长明显放缓.针对选课数据,可以解释为25%左右的学生选课范围覆盖了全校大部分课程.
规则数随实体数增加依然呈现对数增长状态,关系如图6所示.图中 4条曲线分别为全部规则数、支持度大于60%、大于80%以及大于95%规则数,其中,支持度计算中未考虑定义7中的强度影响.随着支持度要求的提升,规则数量增长愈加缓慢.针对测试数据集,这种趋势表现出数据两个特点:一是有一小部分实体的状态序列是缺乏规律性的,可以解释为选课的随意性或者有课程重修,时效规则中环路较多,选择合适的支持度即可过滤掉大部分这类规则;另一方面,数据又表现出大多数实体的状态序列是较为规律和稳定的,只要支持度设定合理,可以用来实现较高可靠性的时效顺序恢复.

Fig.5 Trend chart of the number of states increases with number of entities图5 测试数据集中状态数随实体数增加变化情况

Fig.6 Trend chart of the number of rules with different supports varies with number of entities图6 不同支持度的规则数随实体数增加变化情况
(2) 考虑强度参数的规则支持度
参见定义7及相关解释说明,部分高支持度规则重复出现次数是很少的,是个别现象甚至是特例,不足以作为规则用于数据修复.为了使测试更加客观,实验测试了规则强度对规则数量的影响.引入强度函数后,新的支持度为原支持度与强度函数的乘积.实验中采用Logistic函数作为强度函数:

其中,k和x0应根据数据特征和具体需求设置:k>0,其值越小,f(x)增长越慢;x0≥0,当x=x0时,f(x)=0.5.加入x0的目的是使函数向右平移,以满足函数f(x)值域为(0,1).本次实验中,设定k=0.5,分别测试了x0=5,x0=10对规则数量及修复数据正确率的影响.x0=5时,当某条规则出现5次时,其强度函数值为0.5;出现10次时,强度已超过0.9;出现15次时,函数值已超过0.99.出现次数越多,强度值无限接近于1.
未考虑强度的规则数随状态数增长情况如图7所示.理论上,n个结点的完全有向图含有n(n-1)条边,状态数为结点数,规则数为边数.但对于绝大多数数据集来说,用于时效规则提取的状态都不会是无限的,应该是一个有限集合,这也决定了规则数量也是有上限、可预期的.在图7中也可以明显看出,高支持度规则数的增长速度是明显慢于低支持度规则增长速度的.
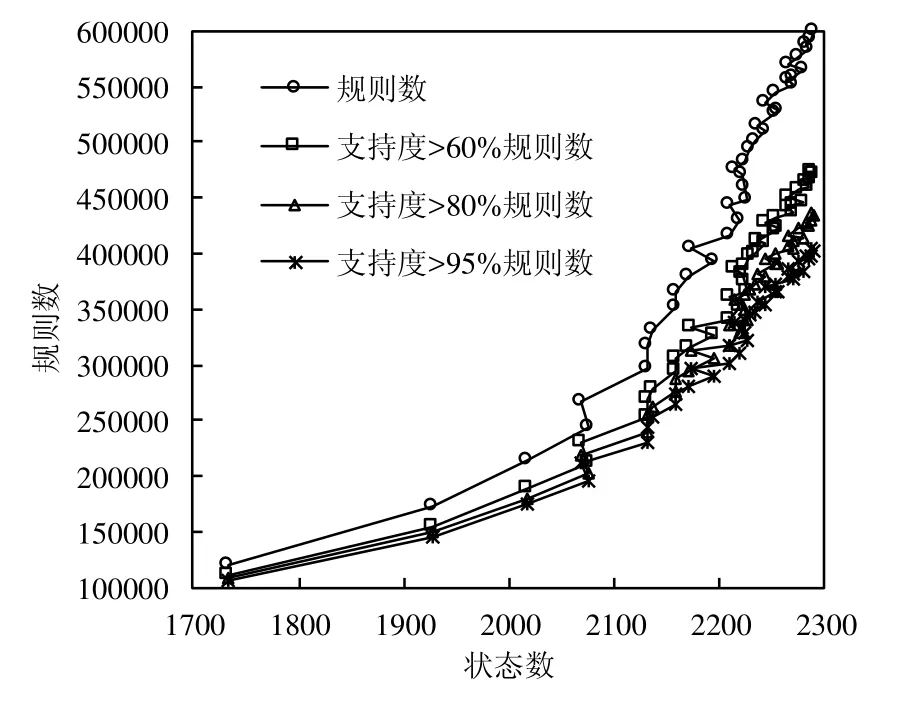
Fig.7 Trend chart of the number of rules with different supports varies with number of states图7 不同支持度的规则数随状态数增加变化情况
加入支持度强度指标后,规则数与状态数关系如图8所示.当实体数为8 000,k=0.5,x0=5时,支持度大于60%,80%,95%规则数分别是总规则数的 30.7%,23.7%,16.5%;x0=10时,上述 3个支持度的规则数分别是总规则数的21.7%,18.2%,13.7%,且3个百分比梯度更小,规则的集中度更高.可见:强度的设置清理了大量重复率低、时效代表性差的规则,大幅缩减了规则数量.x0的取值可根据噪声粒度合理选择,较大的取值虽然可以过滤更多低重复规则,但也可能把一些重复次数较少但有效的规则排除在外.
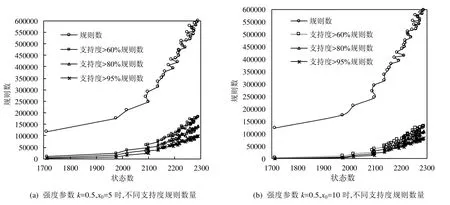
Fig.8 Low frequency rules are greatly reduced after considering rule strength图8 考虑规则强度后低频次规则大幅减少
(3) 提取规则算法效率测试
效率实验中,主要记录了提取规则耗时和整理规则耗时情况.整理规则的主要任务是对规则进行清理和计算规则支持度.提取(或发现)规则耗时与实体数增加呈线性关系,整理规则耗时随实体数增加呈现对数增长趋势.实际上,整理规则耗时随规则数增长线性增加,规则数随实体数对数增长(如图9所示),所以整理规则耗时随实体数对数增加.算法 1具体实现中使用了哈希表数据结构,计算规则支持度等处理效率非常高,能在 3 000ms数量级处理60万条原始规则.而且算法1是可以进行并行化改造的,规则的提取可以分布式完成,满足大数据集处理的时效性要求.
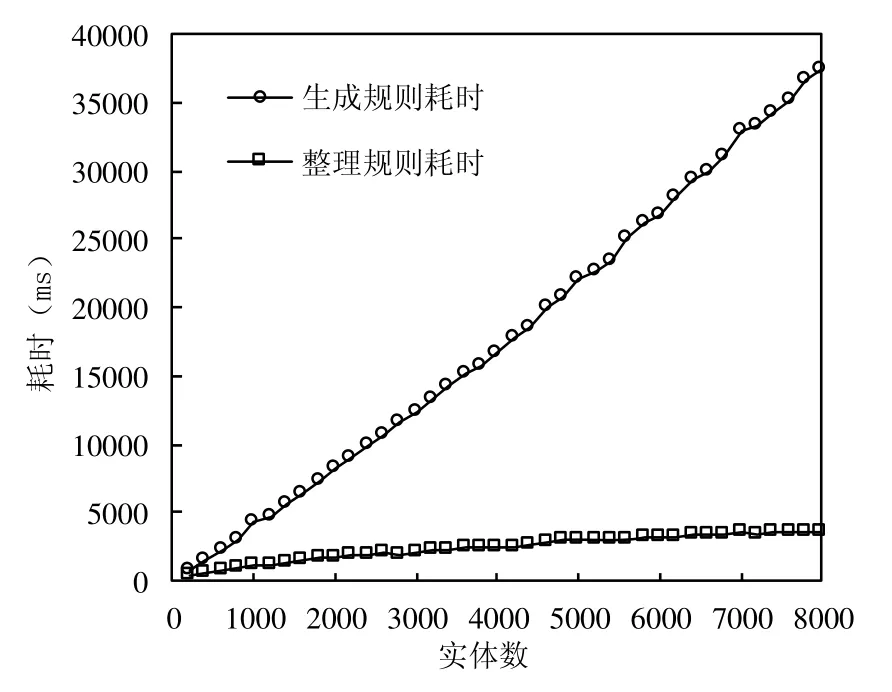
Fig.9 Efficiency test of rule discovery and rule post-processing图9 规则发现和规则整理运行效率测试
3.3 数据时效修复结果分析
(1) 数据时效修复测试方案
(A) 依次设置时效修复规则的支持度S>60%,S>80%,S>95%,执行步骤(B);
(B) 在数据集1中依次随机选取实体数N=200,400,600,…,8000完成时效规则的提取,执行步骤(C);
(C) 在数据集2中依次随机选取2000,4000,…8000个实体,每个实体随机选取1条记录做修复实验,记录修复耗时及正确率.其中,正确率=本次修复成功的记录数/本次修复测试的数据条数.
(2) 数据时效修复效率测试
实验设置在数据集1中取不同数量实体用于规则提取, 采用相同的支持度(S>0.6)分别对数据集2的2000~8000条记录进行时效修复实验.实体数与记录修复耗时关系如图10所示.

Fig.10 Time-consuming of data currency repairing algorithm图10 数据时效修复算法耗时情况
实体数增加到一定程度之后,时效修复耗时基本稳定不变.分析算法 2可知:由于时效修复中也采用了哈希表数据结构,理想情况下,每条记录的时效修复耗时与实体数、规则数无关,为常数阶复杂度O(1).实际测试中,普通PC可在800ms数量级完成8 000个实体记录修复,执行效率可以满足大规模数据时效修复要求.
(3) 规则支持度对数据修复正确率的影响
实验设置在数据集1中取不同数量实体用于规则提取,分别采用不同支持度的规则(S>0.6,S>0.8,S>0.95)对数据集2的8 000条记录进行时效修复实验.实验分两轮:
· 第1轮测试中,强度函数k=0.5,x0=5;
· 第2轮k=0.5,x0=10.
分别测试强度函数x0的取值和不同支持度规则对数据修复正确率的影响.不同规则支持度下,修复 8 000条记录正确率随实体数增加变化情况如图11所示.由图可见:
· 第1轮实验中,在实验数据集上实体数2 000左右是个转折点:在此之前,使用支持度S>0.6的规则修复正确率最高,使用支持度S>0.95的规则修复正确率最低;其后则逐渐反转,规则支持度越高,时序修复正确率越高;
· 第2轮实验中,转折点出现在实体数3 000左右,且实体数较少时相较第1轮实验的数据恢复正确率明显偏低,体现出x0取值对低重复规则的过滤作用较强.
结合图11可以发现:当实体数达到 2000~3000左右时,状态数增长明显放缓.产生这种情况的原因是:实体数小于一定阈值时,状态数不足,此时强度函数中x0的取值对结果影响较为明显,可用的高支持度规则少,数据修复正确率低;当实体数超过某一值后,状态图中的绝大多数结点都已出现,可用的高支持度规则增加,时序修复正确率提高.实验结果表明:当用于规则提取的实体数量足够多时,选择支持度(S>0.95)时,数据时效修复正确率达93%左右,可满足一般应用数据时效修复需求.
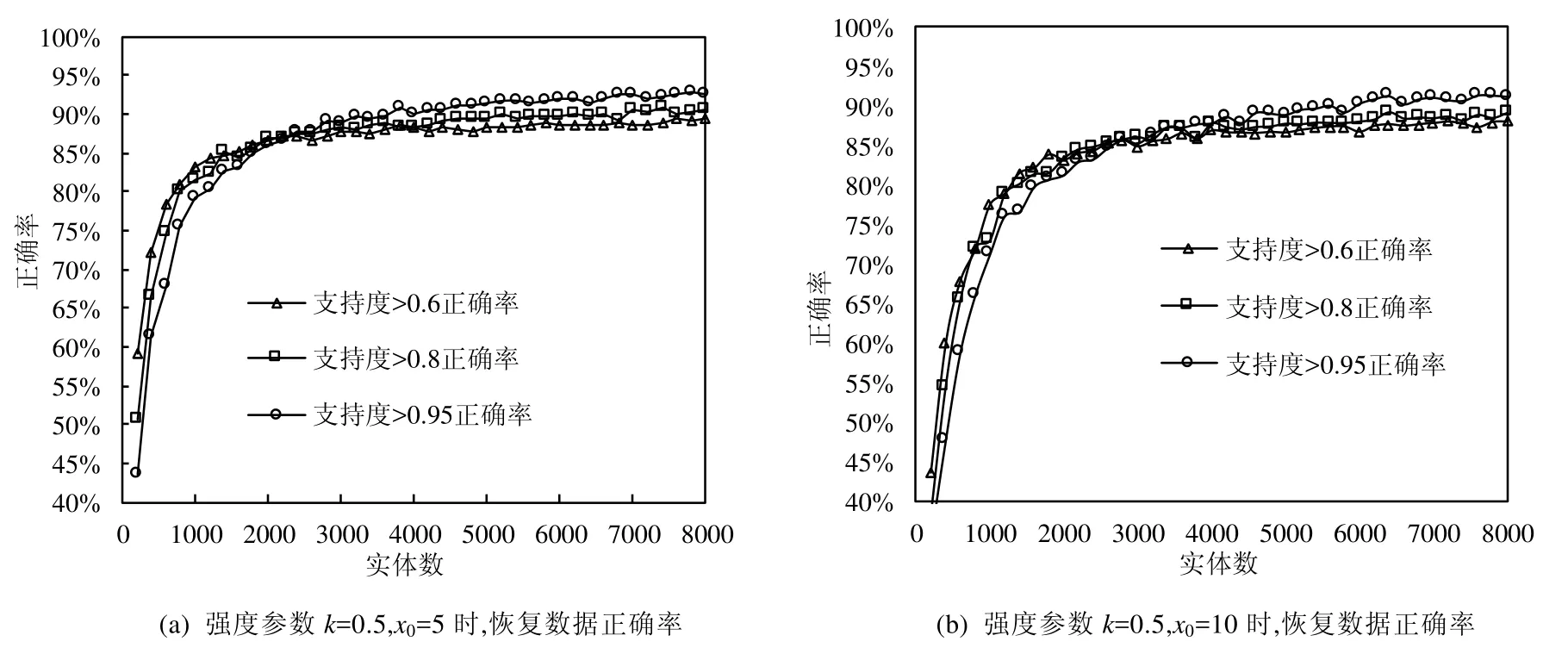
Fig.11 Trend chart of the accuracy of repairing with different rule-supports varies with number of entities图11 不同支持度规则修复数据正确率随实体数变化情况
(4) 规则强度对修复正确率的影响
实验设置在数据集 1中取不同数量的实体用于规则提取,分别在考虑规则强度和不考虑规则强度情况下的支持度(S>0.6)对数据集2的2000~8000条记录进行时效修复实验.实验结果表明,
· 考虑规则强度的情况下(k=0.5,x0=5),数据修复正确率波动小,修复数据一致性好,但是实体数少时正确率偏低,如图12(a)所示;
· 未考虑规则强度时,数据修复正确率波动较大,但实体数少时正确率相对较高,如图12(b)所示.
导致这种现象的原因是:实体数偏少时,高支持度规则数量不多,造成数据修复正确率波动较大;随着实体数量增加,高支持度规则数量逐渐趋于稳定,数据修复正确率也趋于稳定.在考虑规则强度的情况下,选择合理的支持度是稳定提高数据修复正确率的有效方法.
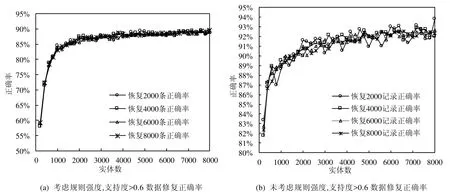
Fig.12 The effect of rule strength on data currency repairing accuracy图12 规则强度对数据时效修复正确率的影响
4 小 结
本文针对同一实体对应的多条记录存在时间戳缺失或不精确条件下的数据时效修复问题进行研究,进一步明确了数据时效问题的相关概念和定义,给出了通用的状态类型时效规则提取算法,不需专门领域知识即可完成基于时效规则的提取.研究还给出了基于时效规则的数据时效修复算法,并在真实数据集上对算法参数设置、运行效率、时效修复正确率进行了测试和验证.时效规则提取算法直观易于实现,时序修复算法效率、修复正确率较高,可满足一般应用要求.
在此基础上,下一步研究工作将重点集中在以下几个方面:
(1) 研究在存在违背函数依赖、条件依赖等情况的非一致的数据集上的时效修复问题;
(2) 研究时序修复方法在检测数据集可能存在的时效冲突中的应用,用以改进数据质量;
(3) 研究结合时效规则的函数依赖、条件依赖方法在数据质量评价中的综合应用.

