幂律流体椭圆形射流破碎的试验研究
王玉龙,尹 燕,白富强, 2,张 帆,杜 青,彭志军
幂律流体椭圆形射流破碎的试验研究
王玉龙1,尹 燕1,白富强1, 2,张 帆1,杜 青1,彭志军1
(1. 天津大学机械工程学院,天津 300072;2. 天津大学内燃机研究所,天津 300072)
基于高速摄影光学试验平台,通过使用4个椭圆度不同的喷孔与两种工质,研究了幂律流体椭圆形射流形貌与破碎的特征.结果表明:与水不同,椭圆孔产生的“轴转换”不稳定现象在幂律液体中整体衰退明显;液体射流速度较小时,椭圆度对破碎长度的影响较小,而后随着射流速度的增大(小于33m/s),椭圆度对射流破碎的促进作用逐渐增强.轴转换波长与射流速度呈现线性关系,幂律液的波长增长率随着椭圆度的增大而增大.通过试验数据修正了幂律流体椭圆射流形貌模型,并分析了椭圆度、韦伯数、表观雷诺数对于射流不稳定性的影响.
幂律流体;椭圆;射流;破碎
液体的破碎现象广泛应用于工程设备与工程机械之中.对内燃机来说,加快燃油破碎与雾化有利于其动力性能、排放性能的改善,是发动机研究领域的重要课题之一[1-3].
大量研究表明,非圆孔对液体破碎与雾化起着促进作用.在实验方面,Sharma等[4]利用高压共轨实验台研究了喷孔形状、轨压对雾化特性的影响,结果表明在一定条件下非圆孔喷嘴降低了喷雾的贯穿距,明显增大了雾化锥角,能提高雾化质量并加快燃油雾化,促进油气混合.郗大光等[5]测量了不同椭圆度喷嘴下喷雾的雾化特性,并通过分析认为椭圆形增大了射流表面波的二阶扰动.Kasyap等[6-7]实验研究表明液体黏性增大会抑制射流的破碎,椭圆度增大使得射流的不稳定性增大,降低了破碎长度.Wang等[8]通过实验研究了圆形以及三角形、矩形、正方形三种非圆孔低速条件下射流破碎变化规律,结果表明,所用非圆孔均有利于液体的破碎.Rajesh等[9]实验研究了黏性以及异型孔对射流形貌不稳定性的影响规律,结果表明异型孔会提高射流不稳定性,黏性会抑制表面不稳定的发展.此外,在理论方面,Bechtel等[10]使用一维闭合模型,研究了椭圆形射流与液体黏性、表面张力、重力、射流速度对椭圆射流形貌的影响规律. Gu等[11]通过对推导的色散方程求解,研究了黏性对不可压缩椭圆低速射流的影响.Amini等[12]在理论和实验方面研究了椭圆射流的不稳定性,其结果表明:椭圆射流在低速时有较大的不稳定增长率,同等条件下,更易破碎.
上述的研究成果都仅限于牛顿流体,对于近年来受到学者们广泛关注的某些特殊新型替代燃料[13-16],如精细水煤浆、使用聚丙烯酸制备的稳定玉米淀粉水浆、生物碳制备的生物泥浆等,由于会表现出非牛顿流体的特征(如低温时具有幂律流体的特征[13]),使得液体的破碎与雾化过程变得更加复杂,因此在大多数情况下,牛顿流体的非圆孔破碎雾化的结论对其并不适用.虽然Bechtel等[17]依据近似的真空假设给出了非牛顿幂律流体椭圆射流形貌的简化模型,但对于非圆孔(椭圆孔)破碎特征的试验研究,目前还鲜有 报道.
基于自行搭建的高速摄影光学研究平台,试验研究了非牛顿幂律流体椭圆孔射流的破碎规律,同时与牛顿流体破碎规律进行了对比,以期更加深入地解释非牛顿液体的破碎规律与指导相关的工业应用.
1 试验系统
1.1 试验所用液体
目前对非牛顿液体破碎与雾化特征的研究,试验液大多采用替代液.Carbopol 934溶液由于其安全可靠,具有无毒、非牛顿特性稳定、不易受热应力的影响等优点而被研究者们广泛采用.
自行配置溶液,通过在一定体积去离子水中加入一定质量Carbopol 934粉末,在搅拌器中充分搅拌;然后利用NaOH水溶液调节溶液pH值,而后充分搅拌;最后,放置真空干燥箱内静置12h以上,去除溶液内残留气泡,稳定溶液的黏度特性,密封待用.
在流体力学中,幂率流体本构方程通常表述为

(1)
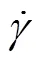
表1 试验流体与几类替代燃料的物性参数

Tab.1 Properties of the tested liquids and several alternative fuels
1.2 试验系统组成
图1为试验装置示意.储液罐内的液体经氮气瓶加压,自喷孔喷出,利用高速相机采集形貌特征.高速相机由日本Photron公司生产,相机型号为FASTCAM SA1.1,相机在5400fps条件下,图片分辨率达1024×1024.高速相机搭载镜头为光圈可调的Canon EF 100mm/2.8L MACRO IS USM微距 镜头.
对于试验所用喷嘴为同一批次加工,其外形结构尺寸相同,喷孔形状不同而横截面大小相同的压力型喷嘴,喷嘴的结构尺寸大小如图2所示.

图1 试验系统示意
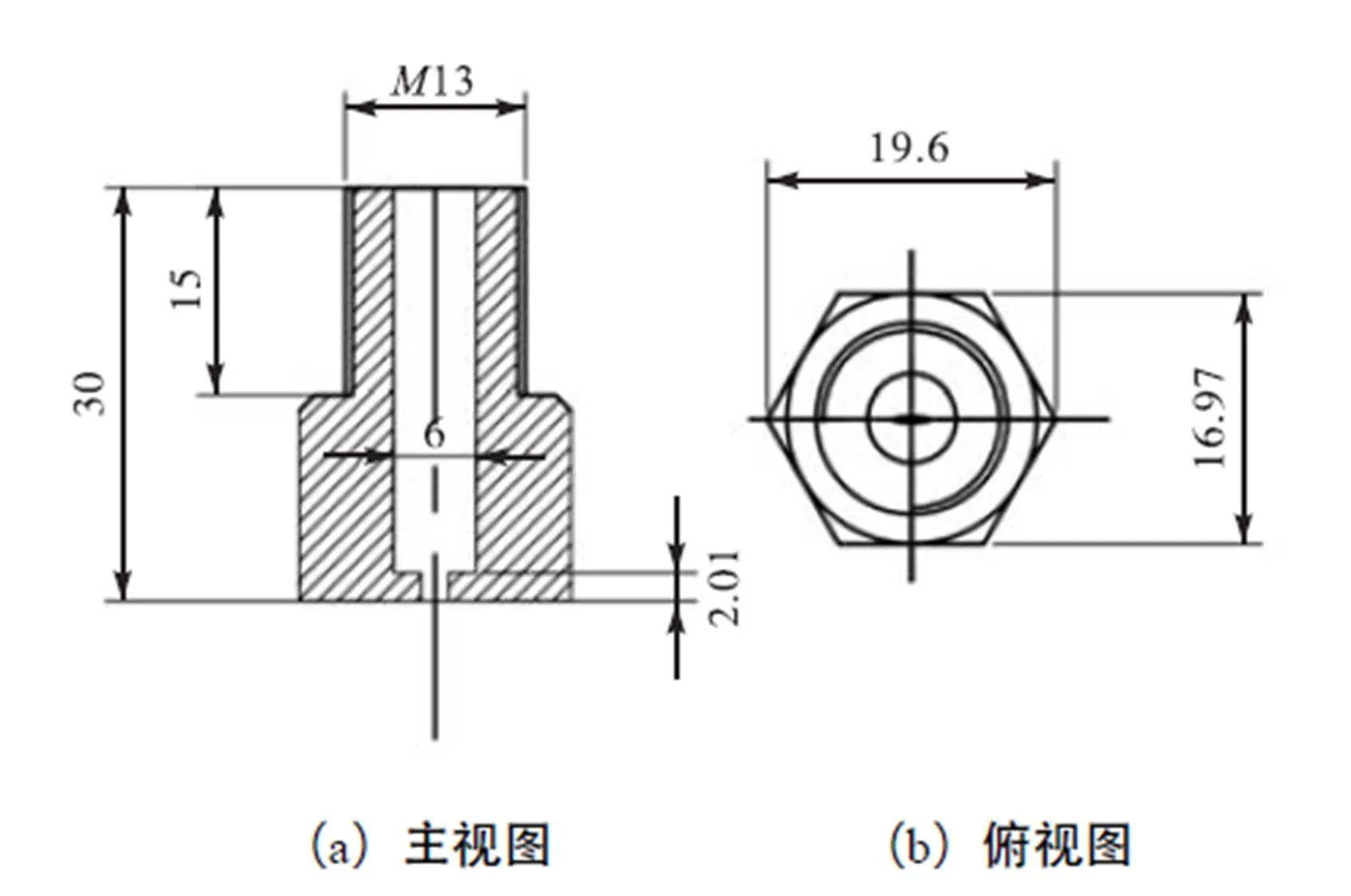
图2 试验所用喷嘴结构尺寸(单位:mm)
通过万用影像型显微镜测得不同喷嘴喷孔的尺寸如表2所示.
表2 椭圆喷嘴喷孔尺寸
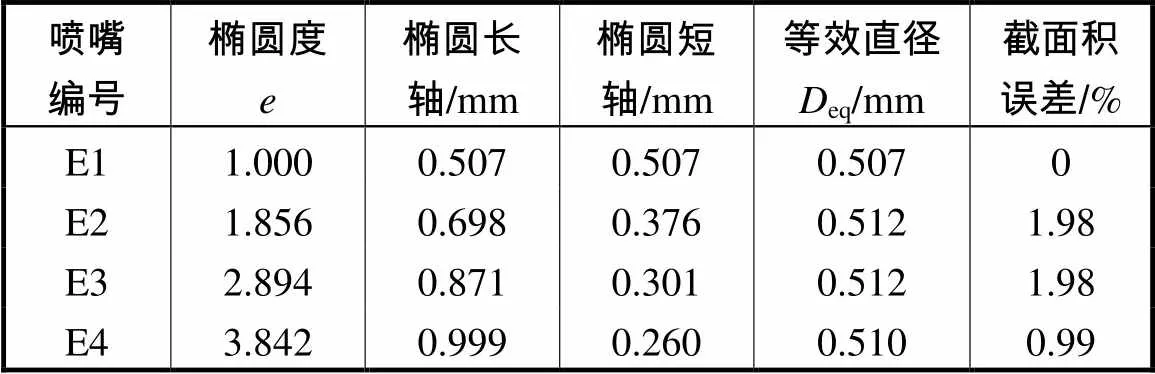
Tab.2 Geometric details of the orifices used in this study
从表2中可以看出,E1喷嘴为圆孔喷嘴,E2、E3、E4喷嘴为椭圆形喷嘴,且4个喷孔的横截面积相差较小,可以忽略截面积的影响.
2 试验结果分析
2.1 喷射压力与射流速度的关系
本试验中依据质量流量法,得到射流的平均出口速度.具体的测量方法为利用脉冲控制器,控制喷嘴的喷射时间T;利用原子秤称取该段时间内喷出的液体质量M;对每一试验工况点重复测量5次,通过质量守恒方程可得出,射流平均出口速度为

(2)
式中:0为射流出口平均速度,m/s;为称重总次数,本试验中=5;M为喷射时间内喷孔喷出的液体净重,kg;T为喷射时间,s;eq为椭圆喷孔等效直径,mm;为液体的密度,kg/m3.
从图3中可以看出,随着喷射压力增大,喷孔出口速度不断增大.此外,对于不同椭圆度的喷孔,在相同喷射压力下,圆形喷孔射流速度最大,椭圆形喷孔的出口速度随着椭圆度的增大而减小.这是由于喷嘴的椭圆度越大,流动损失越大,从而造成射流出口速度的降低.

图3 不同喷嘴射流速度与喷射压力的变化曲线
由图3可见,对于幂律流体,圆孔射流出口速度最大;随着喷射压力不断增大,其他3个不同椭圆度喷孔的出口速度越来越接近.这是由于一方面椭圆度增大,会造成流动损失增大;另一方面,椭圆度越大,喷孔内部的非轴对称性速度梯度造成喷嘴内部流动更加混乱,在剪切变稀特性的影响下,液体表观黏度降低.因此综合考虑流体特性以及喷嘴内部流动沿程阻力损失的影响因素,在试验范围内,不同椭圆度喷嘴的出口速度在相同喷射压力条件下基本相同.
2.2 低速射流破碎特征参数的定义与形貌发展
为了便于表征椭圆射流破碎形貌的变化规律,从椭圆喷孔长短轴(轴、轴)两个垂直的方向拍摄椭圆射流的形貌特征,其拍摄结果如图4所示.
根据质量守恒,从椭圆喷孔流出的液体总体积不变,从图中可以看出,当轴为椭圆长轴时,轴方向为椭圆短轴;而后当轴变为椭圆短轴时,轴变为椭圆长轴;因此,将射流形貌在轴与轴上依次交替出现椭圆长短轴的现象,称为“轴转换现象”.依据射流形貌引入两个射流特征参数:破碎长度b与不稳定波波长.
破碎长度b为在长轴或者短轴拍摄方向上,从喷孔出口位置到射流液柱出现断裂位置的距离.
不稳定波波长为在长轴或者短轴拍摄方向上,喷孔出口处相邻的波峰(或波谷)间的距离.
此外为了便于分析破碎特征参数对射流破碎的影响,分别对特征参数进行无量纲化,得到无量纲破碎长度(beq)和无量纲波长(eq).依据韦伯数(),来获取表征流速的射流无量纲参数——无量纲流速(0.5).

图4 “轴转换现象”与射流特征参数定义
幂律流体椭圆射流破碎过程的形貌发展,与水具有一些不同的特征,其射流发展形貌分别如图5、图6所示.
从图5中可以看到,当介质为水时,椭圆射流在射流速度较低时无轴转换现象;随着射流速度不断增大,轴转换现象逐渐出现,并一直延续到液体破碎.图6显示了射流速度对于非牛顿流体椭圆射流形貌发展的影响.与水椭圆射流类似,在射流表面也会出现轴转换现象.但是,在液体大黏度的影响下,转换波会迅速衰减;随着射流速度的进一步增大,由于幂律流体剪切变稀的流变特性,使得射流出口处流体黏性降低.而黏性对椭圆射流的“轴转换”始终具有阻碍的影响[11],因而使得轴转换的现象延续的时间更长.

图5 韦伯数对于牛顿液体(水)射流形貌变化(E4喷嘴)

图6 韦伯数对于非牛顿液体射流形貌变化(E4喷嘴)
2.3 不同椭圆度对射流破碎的影响
不同椭圆度喷嘴水的射流破碎长度随射流速度的变化关系如图7所示.

图7 水椭圆射流的破碎长度变化
依据射流的破碎机理,低速射流破碎的模式依据射流速度分别为:Rayleigh模式、第一类风声分裂和第2类风声分裂,从图中可以看出,在测量范围内,随着射流速度的增大,圆柱射流的破碎长度呈现出典型射流的“单峰模式”,其峰值点为Rayleigh模式转变为第1类风声分裂的临界点.椭圆射流的破碎长度呈现出“双峰模式”.出现“双峰”主要由于在第1个峰值位置,射流状态发生转变,开始出现“轴转换现象”(结合图5中=16.9),造成较为明显的射流不稳定性,因此随着射流速度的增大,破碎长度减小;产生第2个峰的主要原因和圆柱射流的产生峰值的原因相似,主要由于空气扰动增大,射流状态从Rayleigh模式转变为第一类风声分裂.此外随着射流速度的进一步增大(结合图5=168),射流形貌表面出现了较为明显的“小扰动”,并且随着射流向下发展与轴转换现象导致的液面长短轴变换相互作用,共同影响,促进了射流的破碎.
此外,从图中还可以看出,椭圆度对射流的破碎长度有很大的影响,使得射流的破碎长度明显下降.整体体现为椭圆度越大,破碎长度越短;但随射流速度的增大,这种由喷孔形状对射流破碎的影响逐渐在减弱.
不同椭圆度下幂律流体的破碎长度随射流速度的变化关系如图8所示.
从图中可以看出,在测量范围内(0<33m/s),破碎长度随射流速度的变化呈现为“单峰模式”.当射流速度较小时,不同椭圆度的破碎长度相近,主要由于幂律流体黏性大,“轴转换”现象迅速衰减消失,椭圆度大小对射流破碎的影响较小.然而当射流速度增大到一定程度时,椭圆度对射流破碎长度的影响明显,且随着射流速度的增大,这种促进破碎的作用增强.这是由于椭圆度越大,流体内部的剪切作用越强,流体黏性降低,促进破碎;另一方面椭圆度越大的射流,液柱与空气的接触面越大,使得气液相互作用力会进一步增强,进而促进射流的破碎.

图8 幂律流体椭圆射流的破碎长度变化
2.4 不同椭圆度对射流不稳定波波长的影响
图9为不同椭圆度喷嘴不稳定波波长随射流速度的变化关系.
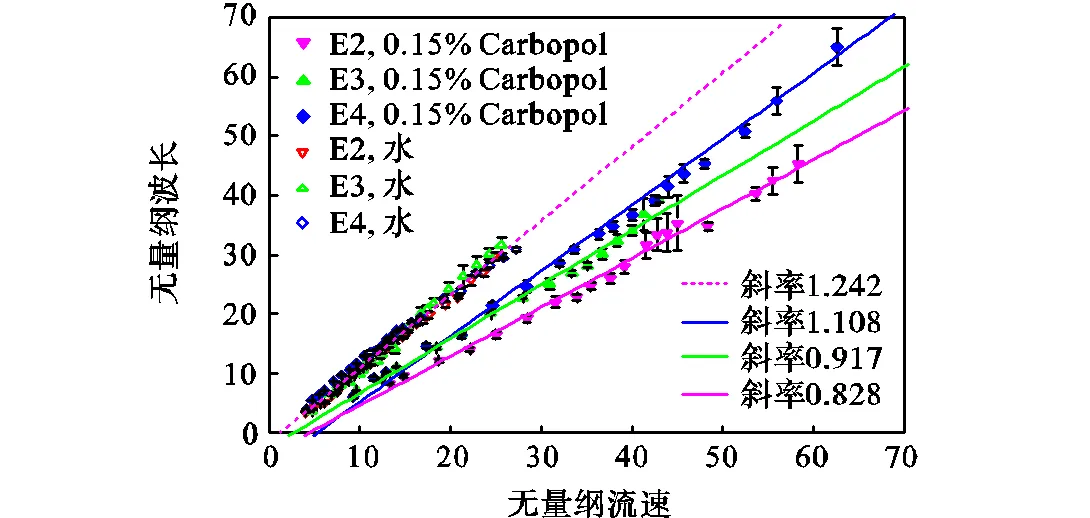
图9 不稳定波波长随射流速度的变化关系
从图中拟合的直线可以看出,不同液体射流的不稳定波波长随射流速度呈线性变化的关系.然而对于水在一定椭圆度条件下,波长增长率与椭圆度的大小无关,其大小约为1.242;然而对于幂律流体,椭圆度对波长增长率有较为明显的影响作用.椭圆度越大,其射流的波长增长率越大.但幂律流体椭圆射流的波长增长率整体比水偏小.
2.5 椭圆射流形貌模型
根据参照Bechtel等[17]对幂律流体自由射流表面方程的描述:将流体视为不可压缩流体;忽略了空气、压力以及重力对射形貌的变化影响;此外认为轴向方向上,忽略黏度梯度、黏度以及表面张力的影响.在此初始射流假设条件下,给出了幂律流体椭圆射流的一维无量纲形貌方程:

(3)

(4)

(5)

(6)

(7) f1=2Φ1(z,T)/Deq
式中:1为无量纲半长轴;0为轴无量纲尺度(文中取10mm);为衡量椭圆射流狭长度参数,取值一般远小于1;为椭圆射流曲率.
公式(3)可以看作为1(,Re,,)=0的函数,当=1时,方程退化成牛顿流体射流形貌.方程则变为

(8)
幂律流体射流模型由于其部分假设条件的简化,使得与实际射流形貌大小会存在较大的偏差.偏差主要来源于假设条件中的射流表面剪切率定义、射流出口速度分量的定义以及忽略气液相互总用力的影响等.与实际射流相比,这些偏差会造成射流形貌不稳定波波长偏大、不稳定波振幅变大的影响.在依据大量试验数据对模型中主要涉及轴转换波长项与轴转换衰减项的系数进行修正,修正后得到的模型为


(9)
图11为试验拍摄射流形貌与修正模型计算得到射流形貌的对比图(E喷嘴,=0.546,=605,Re=2618.34),其中(a)为试验拍摄图,(b)为同工况下原模型射流形貌图,(c)为同工况下修正模型射流形貌图.从图中可以看出,对于修正后的射流形貌模型能够较准确表征椭圆射流形貌的发展规律.

图11 不同模型与试验形貌对比
此外,为了进一步验证模型中速度对射流形貌影响的准确度.通过模型计算得到的无量纲波长与试验无量纲波长进行了对比,如图12所示,图中给出了E3喷嘴与E4喷嘴,无量纲波长试验与模型修正前后计算的对比图.蓝色直线为试验拟合E4喷嘴的斜率,大小为1.018;绿色直线为试验拟合E3喷嘴的斜率,大小为0.917.通过对比可知,修正模型的计算结果与试验数据有良好的一致性,因此该修正模型在一定射流速度条件下对幂律流体椭圆射流形貌的计算具有一定的准确度.

图12 幂律流体波长模型结果与试验对比
最终通过修正模型分别研究了椭圆度、、Re、对射流形貌的影响规律,如图13所示.
图13(a)给出了在=406、Re=2014、=0.546的射流参数下,不同椭圆度对无量纲半长轴射流形貌的影响规律.从图中可以看出,的增大使得射流形貌变得更加不稳定,不稳定波的幅值增大.此外,通过不稳定波波长的变化趋势可以明显看出,的增大使得波长变大,射流振荡的频率降低.
图13(b)给出了在=3.842、Re=2014、=0.546的射流参数下,不同对无量纲半长轴射流形貌的影响规律.从图中可以看出,的增大使得对射流形貌不稳定波波长增加,明显降低了不稳定波的振幅.这是因为的增大使得射流速度也增大.
图13(c)给出了在=3.842、=605、=0.546的射流参数下,不同Re数对无量纲半长轴射流形貌的影响规律.从图中可以看出,Re数改变显著影响了不稳定波的幅值.其主要表现为Re越大,射流振荡越强,黏性对不稳定波的衰减作用越弱,Re对波长有略微提高的作用.
图13(d)给出了在=3.842、=406、Re=2014的射流参数下,不同对无量纲半长轴射流形貌的影响规律.从图中可以看出,值越低,不稳定波波长越大,振幅越大.因为越小意味着射流表观黏度在减小,总体对射流的影响效果与黏度有着相似的作用.
总的来说,增大、、Re或者减小均可以促进椭圆射流的不稳定作用.

图13 不同射流参数对无量纲半长轴射流形貌的影响
3 结 论
(1) 由于喷孔形状的非轴对称,椭圆形喷孔射流会出现“轴转换”现象.幂律流体由于高黏度剪切变稀的物性,使得射流的轴转换振荡现象衰退显著,但随着射流速度的增大,轴转换现象会有略微明显.
(2) 试验液体为水时,椭圆射流破碎长度随射流速度的变化趋势呈现出“双峰模式”;而幂律流体的变化趋势呈现出“单峰模式”.
(3) 轴转换波长与射流速度呈现出线性关系;水的波长增长率与椭圆度无关;而幂律流体其波长增长率比水偏小,随着椭圆度的增大而增大.
(4) 修正了适用于幂律流体的椭圆射流形貌模型.幂律流体椭圆射流中、、Re的增大或者减小起到促进椭圆射流不稳定的作用.
[1] 卫海桥,李 楠,潘家营,等. 甲醇和甲醇重整气对直喷汽油机性能影响的对比研究[J]. 内燃机工程,2018(1):15-22.
Wei Haiqiao,Li Nan,Pan Jiaying,et al. Effect of methanol or methanol reformate addition on GDISI engine performance[J].,2018(1):15-22(in Chinese).
[2] 徐阳杰,虞育松,李国岫. 超临界环境下的雾化过程中表面张力变化对射流稳定性的影响[J]. 燃烧科学与技术,2017,23(2):111-115.
Xu Yangjie,Yu Yusong,Li Guoxiu. Effects of change in surface tension on jet stabilities in atomization process under supercritical environments[J].,2017,23(2):111-115(in Chinese).
[3] 任晓华,张 磊,任泽昱,等. 基于多组分蒸发模型的柴油喷雾燃烧的LES研究[J]. 燃烧科学与技术,2018,24(6):528-534.
Ren Xiaohua,Zhang Lei,Ren Zeyu,et al. Large eddy simulation of diesel spray combustion based on a multicomponent vaporization model[J].,2018,24(6):528-534(in Chinese).
[4] Sharma P,Fang T. Spray and atomization of a common rail fuel injector with non-circular orifices[J].,2015,153:416-430.
[5] 郗大光,龚允怡,彭志军,等. 椭圆孔射流的雾化问[J]. 内燃机学报,1996,14(4):370-377.
Xi Daguang,Gong Yunyi,Peng Zhijun,et al. Atomization of a liquid jet from an elliptical orifice[J].,1996,14(4):370-377(in Chinese).
[6] Kasyap T V,Sivakumar D,Raghunandan B N. Breakup of liquid jets emanating from elliptical orifices at low flow conditions[J].,2008,18(7):645-668.
[7] Kasyap T V,Sivakumar D,Raghunandan B N. Flow and breakup characteristics of elliptical liquid jets[J].,2009,35(1):8-19.
[8] Wang F,Fang T. Liquid jet breakup for non-circular orifices under low pressures[J].,2015,72:248-262.
[9] Rajesh K R,Sakthikumar R,Sivakumar D. Interfacial oscillation of liquid jets discharging from non-circular orifices[J].,2016,87:1-8.
[10] Bechtel S E,Cooper J A,Forest M G,et al. A new model to determine dynamic surface tension and elongational viscosity using oscillating jet measurements[J].,1995,293:379-403.
[11] Gu S,Wang L,Dls H. Instability evolution of the viscous elliptic liquid jet in the Rayleigh regime[J].,2017,95(6):063112.
[12] Amini G,Dolatabadi A. Axis-switching and breakup of low-speed elliptic liquid jets[J].,2012,42:96-103.
[13] Chen R,Wilson M,Leong Y K,et al. Preparation and rheology of biochar,lignite char and coal slurry fuels[J].,2011,90(4):1689-1695.
[14] Natarajan V P,Suppes G J. Rheological studies on a slurry biofuel to aid in evaluating its suitability as a fuel[J].,1997,76(14):1527-1535.
[15] Abdullah H,Mourant D,Li C Z,et al. Bioslurry as a fuel. 3. Fuel and rheological properties of bioslurry prepared from the bio-oil and biochar of mallee biomass fast pyrolysis[J].,2010,24(10):5669-5676.
[16] 陈良勇,段钰锋,刘 猛,等. 水煤浆真实流变特性的研究[J]. 动力工程学报,2008,28(5):753-758.
Chen Liangyong,Duan Yufeng,Liu Meng,et al. True rheological behavior of coal-water slurry[J].,2008,28(5):753-758(in Chinese).
[17] Bechtel S E,Youssef N T,Forest M G,et al. Non-Newtonian viscous oscillating free surface jets,and a new strain-rate dependent viscosity form for flows experiencing low strain rates[J].,2001,40(4):373-383.
Experimental Investigation on the Breakup Characteristics of Elliptical Power-law Liquid Jets
Wang Yulong1,Yin Yan1,Bai Fuqiang1, 2,Zhang Fan1,Du Qing1,Peng Zhijun1
(1. School of Mechanical Engineering,Tianjin University,Tianjin 300072,China;2. Tianjin Internal Combustion Engine Research Institute,Tianjin University,Tianjin 300072,China)
Based on a high-speed photographic optical experimental platform,the characteristics of elliptical jet morphologies and power-law fluid fractures were studied using four nozzles with different ellipticities and two working fluids. The results showed that,compared with that in water,the axis-switching phenomenon produced by the elliptical hole was significantly degenerated in the power-law fluid. Ellipticity exerted a slight influence on the breakup length at a low jet velocity but gradually promoted jet fractures with increasing jet velocity (<33 m/s). A linear relationship was found between the axis-switching wavelength and jet velocity,and the wavelength growth rate of the power-law liquid increased with increasing ellipticity. The experimental data were used to modify the elliptical jet topography model of power-law fluids. Whereas increases in ellipticity,Weber number,and apparent Reynolds number promoted jet instability,increases in power index,consistency coefficient,and surface tension coefficient suppressed this instability.
power-law liquid;ellpiticity;jet;breakup
TK464
A
1006-8740(2019)02-0161-08
2018-04-20.
国家自然科学基金资助项目(51676135);天津市应用基础与前沿技术研究资助项目(15JCZDJC39600).
王玉龙(1992— ),男,硕士,wangyulong@tju.edu.cn.
彭志军,男,博士,教授,pengzj@tju.edu.cn.
10.11715/rskxjs.R201804036

