预应力加筋土挡墙变形性能研究

杜运兴，袁兰，陈仕文，周芬



预应力加筋土挡墙变形性能研究

杜运兴，袁兰，陈仕文，周芬

(湖南大学 土木工程学院，湖南 长沙 410082)

采用有限差分数值方法研究预应力加筋土挡墙的侧向变形和沉降规律。填料采用双曲线型塑性硬化本构模型，计算过程中考虑填筑和压实过程，采用模型试验的结果验证了数值方法。针对填料的密实度、桥台基础边缘距墙面板距离、预应力筋的轴向刚度建立分析工况。研究结果表明：顶部荷载作用下，预应力挡墙的墙面板位移、顶部沉降均比未施加预拉力的挡墙明显减小；填料的密实度和桥台基础边缘距墙面板的距离对墙面侧向位移影响最大；提高预应力筋的轴向刚度有利于减小挡墙的变形。

模型试验；数值模拟；预拉力；侧向位移；沉降

在无黏结预应力加筋土技术[1]中，加筋体系对填料的约束作用是一种主动的约束。无黏结预应力加筋土结构由预应力筋、墙面板、侧压板和填料构成。对预应力筋进行张拉，可以实现墙面板、侧压板对加筋区填料的约束，从而提高该位置填料的承载力和整体性。该技术中由于存在着墙面板、侧压板、加筋材料和填料之间复杂的相互作用，挡墙的变形性能受到预应力筋中轴向力水平、填料密实度、预应力筋轴向刚度和顶部荷载作用等众多因素的影响。然而，当前无黏结预应力加筋土技术的研究非常有限，使得这一工程结构在应用上受到一定的限制。试验的方法存在成本高、周期长、实测数据有限的缺陷，一种可行的方法是通过试验结果验证数值模型，然后利用验证后的数值模型研究不同的工况，就可以以较低的成本获得更全面的数据。数值模拟结果的可靠性受多种技术因素的制约，其中，适宜的土体本构模型的选用起关键性的作用[2]。土的基本特性有压硬性和剪胀性[3]，压硬性即土的刚度随围压的增加而增大；随围压变化的弹性切线模量相比于固定的弹性模量摩尔库伦模型更符合土体的非线性特性，在岩土计算领域应用广泛。另外，由于加筋土挡墙存在填筑过程，这一过程对挡墙的受力和变形有重要影响[4]。因此，要准确地模拟填筑式挡墙的变形必须考虑施工过程。施工过程的模拟主要通过填料的逐层填筑、压实和相应结构体系的依次激活来实现。对于竖直面板式挡墙，还需要考虑墙面的临时支撑等边界条件的变化。填料的压实可以通过在每层填料表面施加一个临时均布荷载，然后在激活下一层填料前移除来模拟，这种方法已经为众多学者[5−7]所采用。本文采用试验和数值计算相结合的方法研究无黏结预应力挡墙的变形性能。采用具有双曲线应力应变关系的塑性硬化模型[8](简称PH模型)模拟填料，在施工过程的模拟中，考虑填料的逐层填筑压实以及边界条件的变化。通过数值和实测结果对比验证数值模型的可靠性，然后建立一个模拟加筋土桥台的基准工况。在此基础上展开参数分析，研究各参数对该类挡墙的侧向变形和沉降的影响。

1 模型试验

模型试验在砂箱中完成。砂箱尺寸为2.0 m(长) ×0.8 m(宽)×1.6 m(高)，砂箱内侧采用钢化玻璃以减少摩擦对试验的影响。墙面板和侧压板分别为边长0.4 m和0.25 m的方形混凝土板。上下相邻墙面板连接处设置了6 mm厚橡胶垫块来改善墙面板之间的连接。预应力筋采用长0.64 m，直径8 mm的钢绞线，并套于涂油的PVC管内。

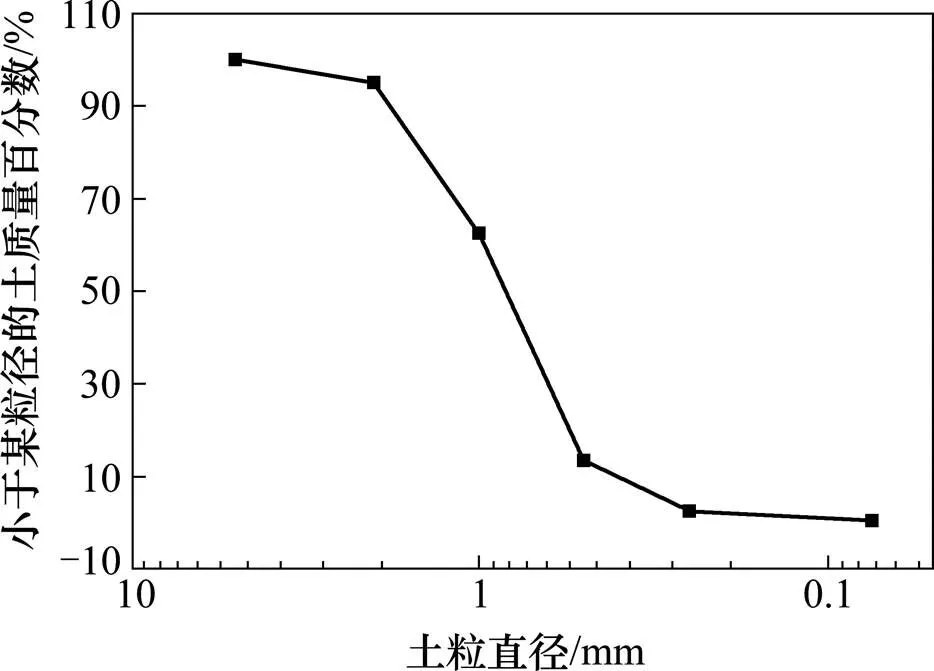
图1 钢砂填料级配曲线图

采用峰值摩擦角为37°，容重为53 kN/m3的混合钢砂作为填料，钢砂的级配曲线见图1所示。每层墙面板高度范围内的填料分4次填筑并压实，每次高度分别达到侧压板底部、中部、顶部以及当前层墙面板的顶部。墙面板在安装过程中利用木支撑固定，并在安装下一块墙面板前移除木支撑。填筑完成后，利用锚固装置分别对第1~第4层预应力筋施加7，5，3和1 kN的预拉力，最后用砝码在非加筋区顶部施加18 kPa均布荷载。作为对比，建立了未施加预拉力的模型，其唯一区别是没有对预应力筋施加预拉力。

2 数值模型

针对试验模型建立的平面应变数值模型如图2(a)所示。图中数字1~5代表建立的不同界面，这些界面分3种类型：1属于混凝土/钢板界面，2，3和5属于混凝土/填料界面，4属于混凝土/橡胶界面。侧压板采用能够抵抗弯矩的梁单元模拟，预应力筋采用只承受轴向力的cable单元模拟，不考虑cable与填料之间的相互作用。每层墙面板支撑用具有轴向刚度truct=100 MN/m的梁单元模拟。挡墙右侧约束方向位移，底部基础约束，方向位移。

施工模拟包含了填料的填筑、压实以及边界条件的变化。填筑过程的模拟是通过由下往上逐步激活填料、墙面板、预应力筋和墙面板来实现的。压实过程则是通过在每层填料表面施加8 kPa均布荷载，并在激活下一层填料前移除该荷载来实现的。填筑过程中边界条件也随之发生变化，如图2(b)所示，是第2层填筑完成时的模型，而在第4层填筑完成后安装第2层墙面板时，支撑1和支撑2已经拆除，并安装了支撑3和支撑4。

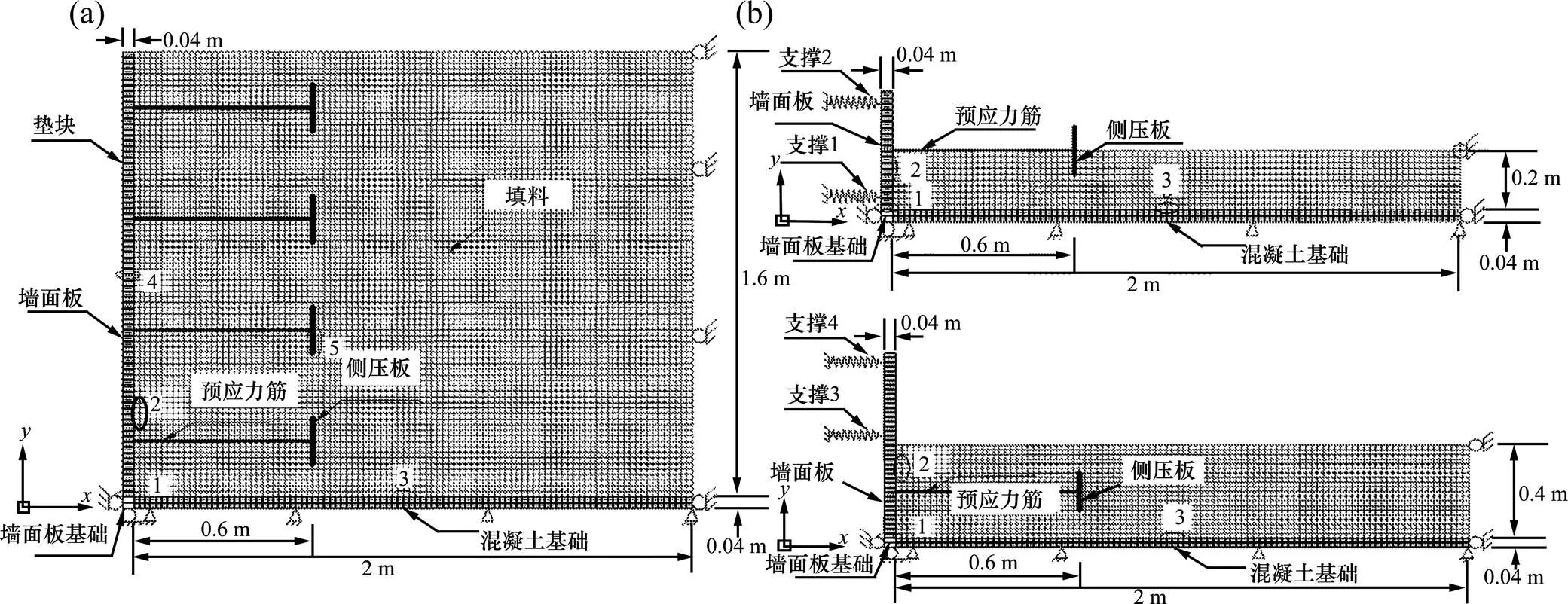
1—墙面板基础/墙面板；2—墙面板/填料；3—填料/混凝土基础；4—墙面板/橡胶垫块；5—侧压板/填料

采用PH模型[8]模拟钢砂填料的应力应变关系，该模型引入了摩尔库伦破坏准则并考虑填料的非线性和剪胀性。填料参数通过三轴试验来标定。PH模型利用围压相关的50代表土体的刚度参数(式(1))，并具有双曲线型的应力应变关系(式(2))该式的图形表达如图3所示。

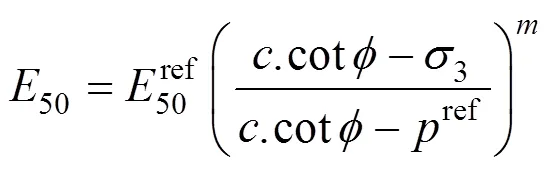
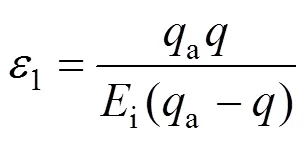
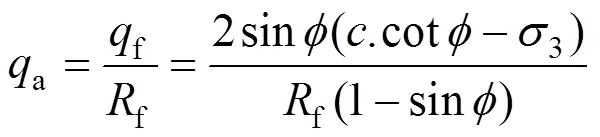
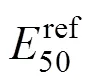
数值计算所用填料参数见表3，其余材料均采用线弹性模型模拟，其参数见表1，界面参数见 表2。

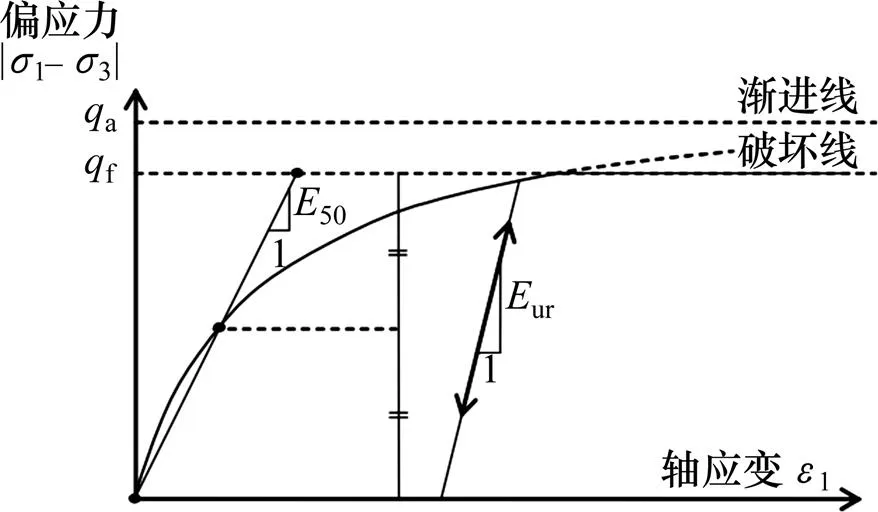
图3 PH模型中应力应变关系

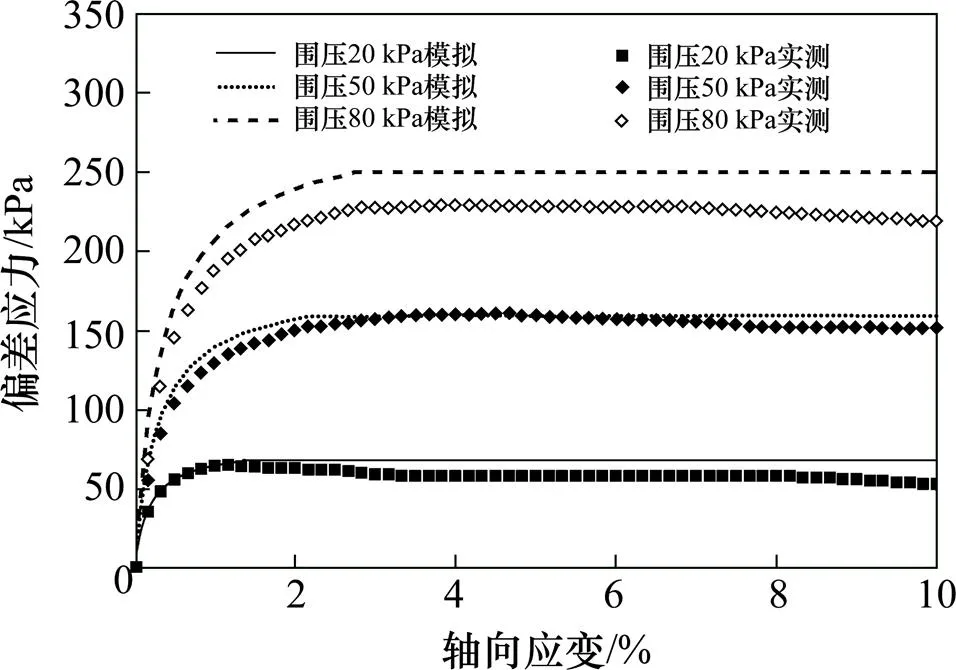
图4 填料三轴试验结果

表1 数值模型中各材料参数

表2 界面参数

3 结果对比

图5对比了实测和计算所得的墙面板侧向位移。在上下2层墙面板相接位置(=0.4，0.8和1.2 m)对应着2个位移，这说明相邻墙面板之间出现错动，与模型试验过程中观察到的现象是一致的。填筑完成时实测墙面板的侧向位移发生在最下层，达到4.9 mm。计算所得墙面位移总体呈现中下部大，上部小的分布规律，最大位移达到4.6 mm。在顶部荷载作用下，预应力挡墙侧向位移有一定增大，但并不明显，计算最大位移仅为4.8 mm。然而对于不施加预拉力的挡墙，顶部荷载下计算的最大侧向位移达到7.4 mm，比施加预拉力情况下的侧向位移增大54.2%。

温馨提示：因为白薯的淀粉含量高，换算成米饭的时候就不能按照4∶1了，要按3∶1才对，所以说当你吃3份白薯的时候，你当天吃的米饭的量就得减少1份了。

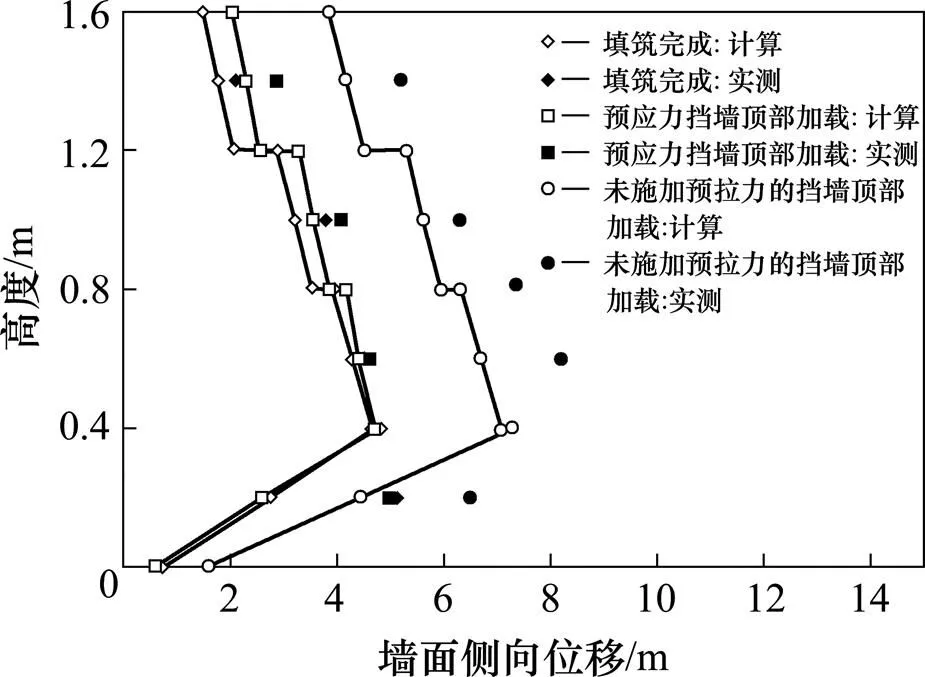
图5 墙面板侧向位移

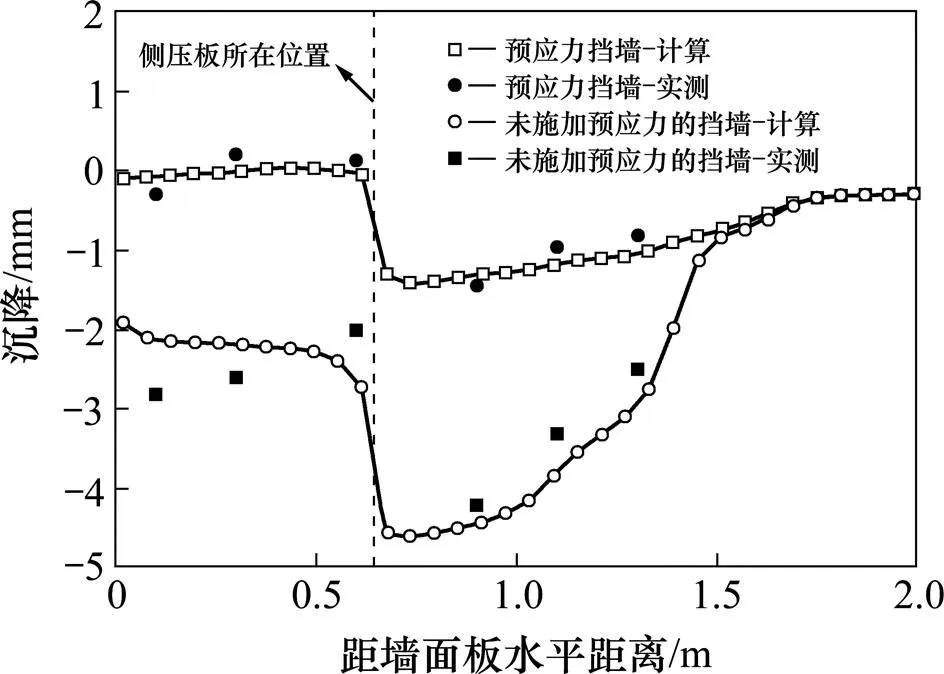
图6 填料顶部沉降

图6对比了实测和模拟所得的墙顶附加沉降。该沉降直接反映了挡墙在荷载作用下抵抗变形的能力。预应力挡墙在顶部荷载作用下产生的最大附加沉降量为1.41 mm，仅为未施加预拉力的挡墙情况下的31%。这说明施加预拉力能够显著提升挡墙的刚度，在荷载作用下具有更大抵抗变形能力。结合图5~6可知，计算和实测数据吻合度良好，这证明所建立的数值模型能够合理地预测挡墙变形。

4 参数分析

4.1 基准工况

利用与第2节相似的建模方法建立了一个基准工况，以模拟实际工程中的加筋土桥台的变形特性。以基准工况展开参数研究，研究变量包括预应力筋轴向力水平、填料密实度，预应力筋的轴向刚度、墙面板基础相对刚度、桥台基础位置、桥台基础荷载大小。每个研究工况都是在基准工况的基础上单一地改变研究变量来进行参数研究的。

基准工况的有限差分网格和局部放大图如图7所示。墙面、填料、墙面板基础和填料基础分别由1×60，79×60，1×2和79×2个网格构成。模型右侧约束方向位移，底部基础约束，方向位移，填料基础和墙面板基础均约束方向位移。假设墙面板基础以及填料位于Winkler地基上，这种假设可以研究基础的竖向可压缩性对挡墙变形的影响。将0.25m厚度的地基土设置为弹性，并将其泊松比设置为0来模拟Winkler地基(参见Damins 等[10])，在基准工况中，墙面板基础和填料基础具有相同刚度，基床系数=4×104kN/m3。这样的地基实际等效为受到水平向固定，竖向为弹簧约束的边界条件(图7)。数值模型中采用100kPa等效荷载来替代桥台基础的作用，荷载水平与Abu-Hejleh 等[11]在Founders/Meadows 加筋土桥台现场试验的实测值115 kPa很相似。

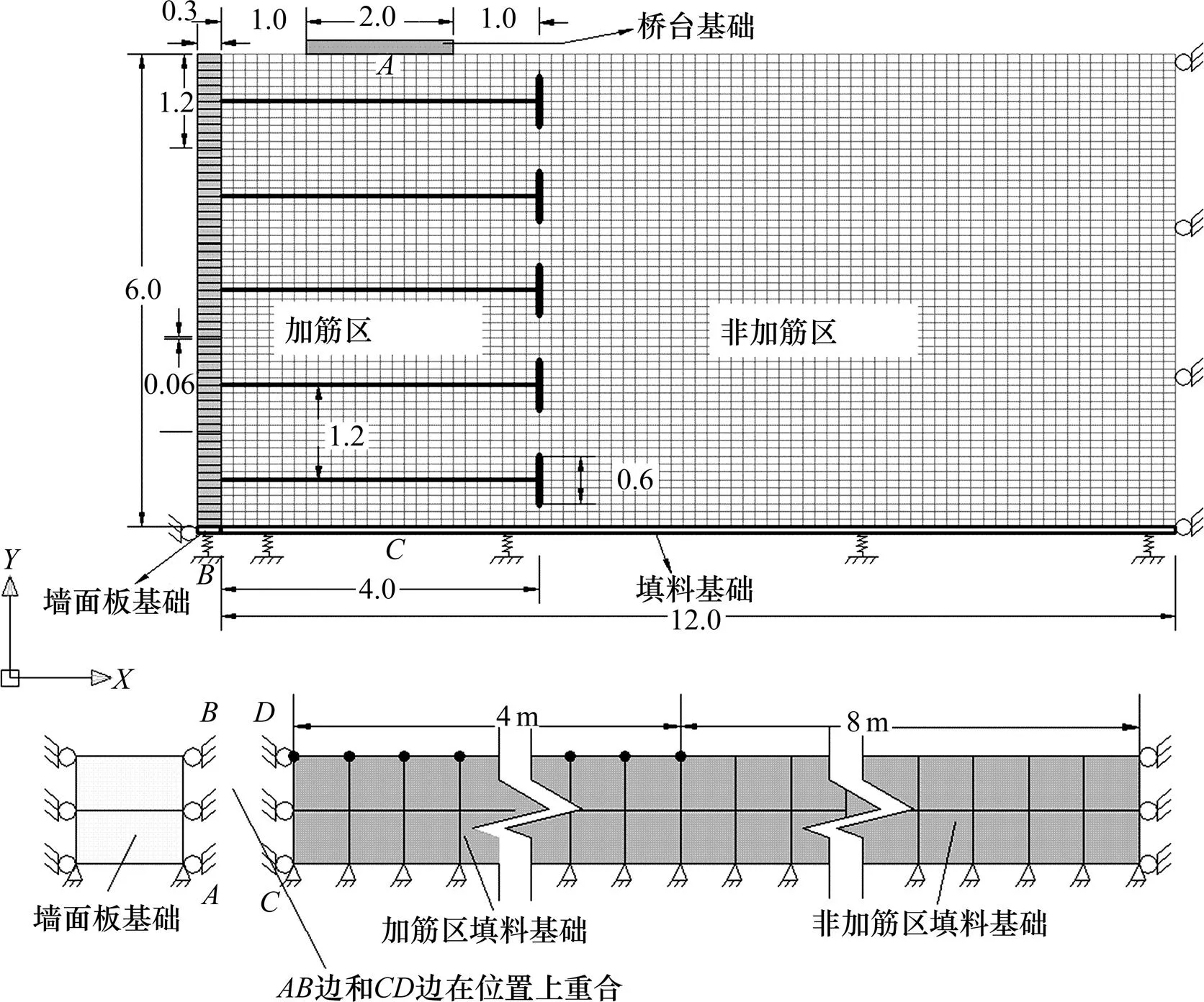
单位：m

填料为中等密实度的无黏性填料，其计算参数来源于文献[8]，并汇总于表3中中砂所在列。标准工况设有5层预应力筋，每层预应力筋的沿墙走向方向水平间距为1 m，竖向间距1.2 m。1~5层预应力筋轴向力水平分别为60，50，40，30和15kN。预应力筋的轴向刚度通过式(4)来定义：

式中：，和分别是预应力筋的横截面面积、弹性模量和长度。基准工况中预应力筋的刚度为1×107N/m。

如图8所示，本文通过墙面板侧向位移，以及沉降A，B和C来衡量挡墙变形性能。A，B和C分别代表桥台基础沉降、墙面板基础沉降和加筋区范围内填料基础平均沉降。由于基础采用了线弹性模型，其沉降与基础所受到的竖向土压力成比例，因此基础的沉降能够衡量基础所承受的土压力大小。在基准工况中，100 kPa桥台基础荷载作用下，挡墙的最大侧向位移为8.66 mm，发生在面板2和面板3衔接处。最大的沉降为14.88 mm，发生桥台基础作用位置处。

4.2 预应力筋中轴向拉力水平的影响

合理的预拉力的大小是实现无黏结预应力加筋土技术的关键。以基准工况中施加的轴向力为标准值，分别研究轴向力为0.75倍、1.0倍和2.0倍标准值以及不施加预拉力的挡墙变形。如图8所示，墙面侧向位移随着筋带轴向力水平的增大而明显减小，且最大位移均位于墙面中部。最大侧向位移从不施加预拉力情况下的11.74mm减小至2倍标准值轴向力情况下的6.60mm，减幅为43.8%。同样，桥台基础的沉降量从不施加预拉力的19.06 mm减小到2.0倍基准工况轴向力情况下的12.09 mm，减幅为36.6%。基础B和C的沉降量几乎不受到轴向拉力水平的影响。沉降A最大，B次之，C最小，在后文的其他参数分析中也主要呈现这个规律，A最大是因为它包括了6m厚填料的压缩量，B比C大则是因为墙面板基础比填料基础承受着更大的竖向应力，这在YU等[7]的研究报告中得到证实。综上可知，适当地加大预应力筋的轴向拉力有助于减小挡墙的变形。

表3 填料的参数

*所在行数据对应基准工况，模型参数含义见文献[8]

(a) 墙面侧向位移；(b) 沉降

4.3 填料密实度的影响

对3种不同密实度的无黏性填料进行了参数分析。由图9(a)可知，墙面(尤其是中部墙面)的侧向位移随着填料密实度的增大而显著减小，最大的侧向位移均发生于墙面中部，从松砂的18.72 mm减小到密砂的6. 22 mm。由图9(b)可以看出，密实度对桥台基础、墙面板基础、加筋区填料基础的沉降的影响依次减弱。当填料密实度较低时，墙面板最大位移和桥台基础的沉降随密实度的增大显著减小。松砂时的墙面最大位移和桥台基础沉降分别是密砂时的3.01倍和2.60倍。由此可见控制填料具有较高的密实度，对于减小墙体变形具有十分重要的意义。

4.4 预应力筋轴向刚度的影响

在无黏结预应力加筋土挡墙设计中，预应力筋的轴向刚度是必须考虑的参数。刚度过大造成资源浪费，刚度过小则极限拉力不足。如图10所示，预应力筋的轴向刚度对墙面板侧向位移有重要影响，当轴向刚度从0.25×107N/m增加至4×107N/m时，墙面最大侧向位移从13.36 mm减小至7.19 mm，减小幅度达46.2%。但当轴向刚度超过2.0× 107N/m时，墙面侧向位移不再明显减小。然而，预应力筋的轴向刚度对沉降几乎没有影响。为了保证该类挡墙具有足够的抵抗变形能力，预应力筋的轴向刚度应不小于0.5×107N/m。Alam等[12]通过有限元方法也得出了相似的结论。

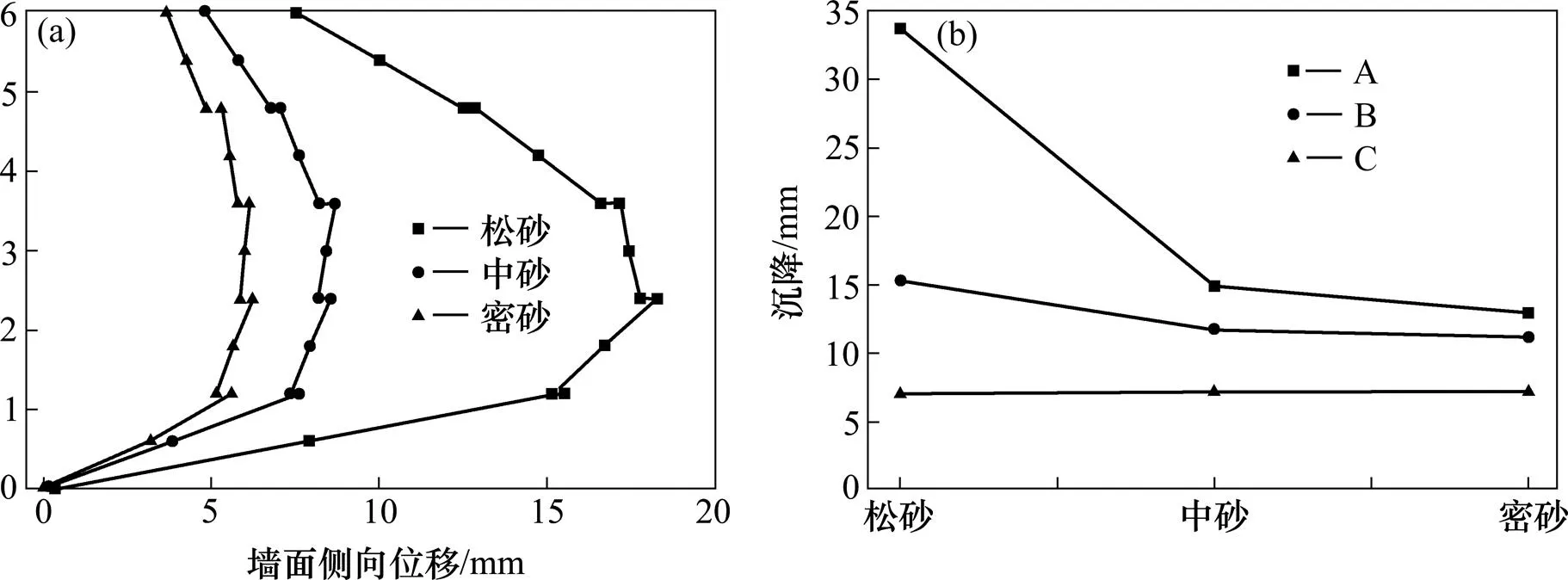
(a) 墙面侧向位移；(b) 沉降

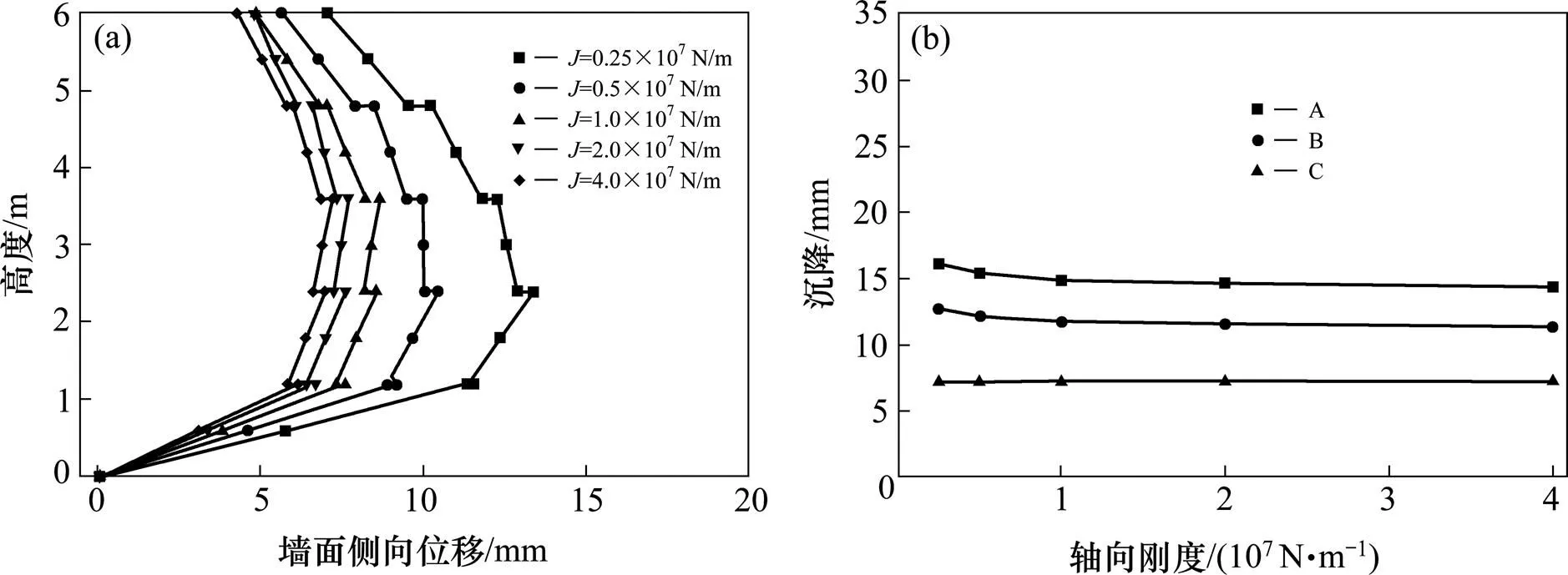
(a) 墙面侧向位移；(b) 沉降

4.5 墙面板基础刚度的影响

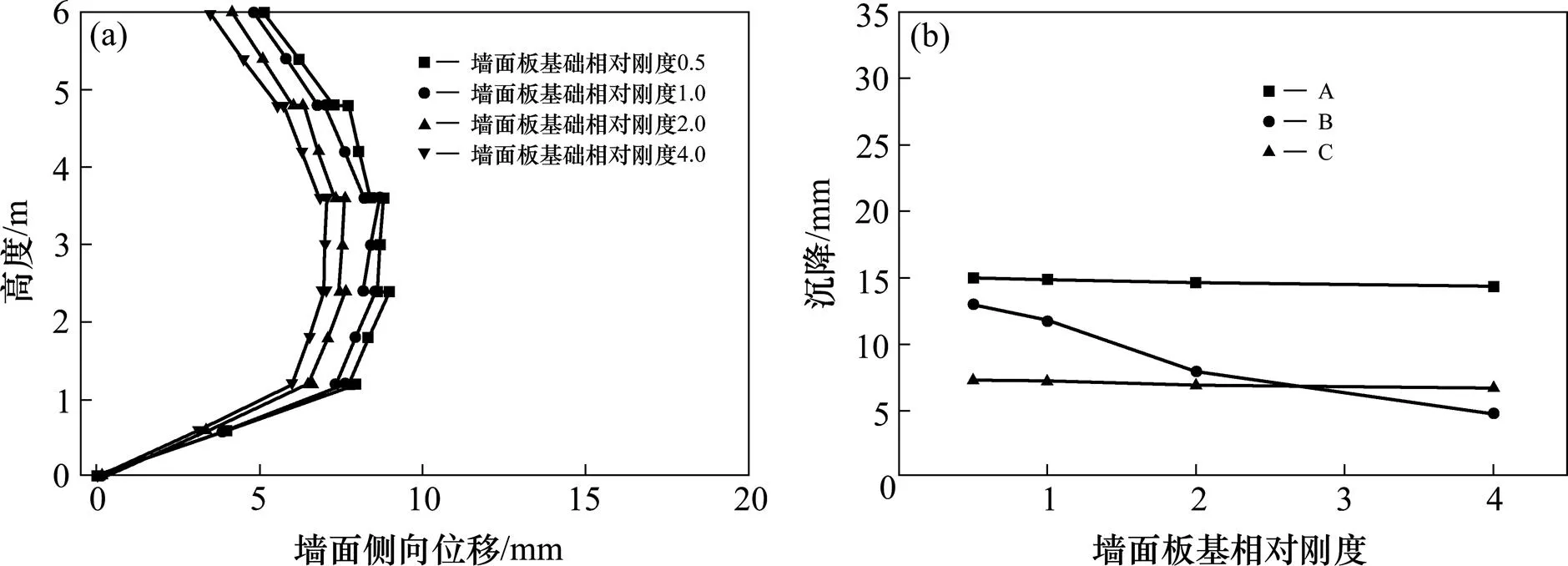
大部分的加筋土挡墙设计均假设地基是刚性的[10]，然而实际工程中，挡土墙基础并非不可压缩。而且在高耸挡墙中，墙面板基础荷载很大，基础处理往往是增加工程造价的主要原因之一[13]。为了探讨墙面板基础可压缩性对挡墙性能的影响，本文保持填料基础刚度不变而对墙面板基础刚度(即基床系数)分别为填料基础刚度的0.5倍、1.0倍、2倍和4倍时的情况进行了参数分析。如图11所示，墙面侧向位移随着墙面板基础刚度的增加而减小，但影响幅度很有限。例如墙面侧向位移从0.5倍刚度时的8.98 mm减小到4倍刚度的7.05 mm，仅仅降低了1.93 mm。沉降A和C几乎不受墙面板基础刚度影响，但墙面板基础B的沉降明显随着其自身刚度的增加而显著降低。当墙面板基础的刚度很大时(例如为4倍的填料基础刚度时)，墙面板基础的沉降B甚至小于C。

4.6 桥台基础位置的影响

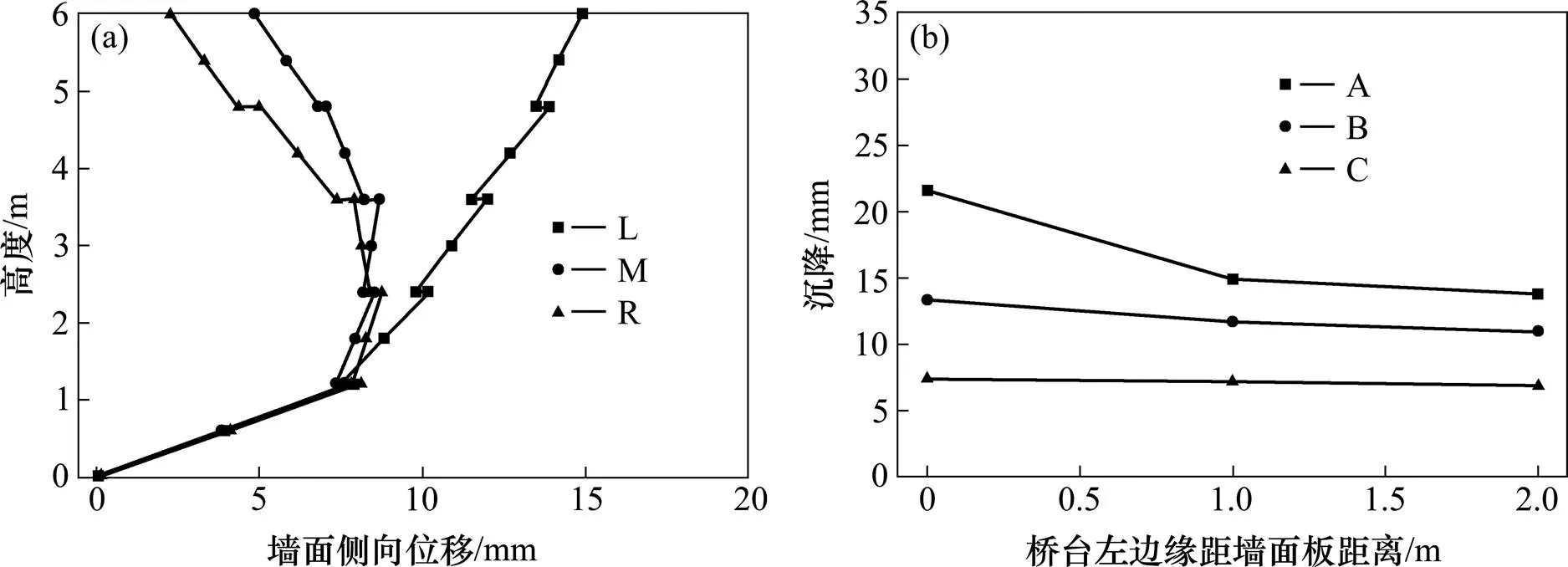
为了研究桥台基础的作用位置对挡墙性能的影响，本文分别对桥台基础左边缘距离墙面板0 m(最左侧L)，1 m(居中M)和2 m(最右侧R)3种工况进行了研究，该范围确保了桥台基础不超出加筋区。如图12(a)所示，桥台基础的位置对于墙面侧向位移的影响显著。桥台基础从R变化到M时，墙面最大侧向位移基本保持不变，顶部侧向位移仅增大了1.1倍。但当桥台基础从M变化到L时，侧向位移最大值由8.65 mm急剧增加到14.89 mm，增幅为72.1%，并且发生最大侧向位移的位置由中部转移到顶部，根据这种变形模式可以判断：桥台距离墙面板太近容易造成挡土墙倾覆破坏。同样的，当桥台位置在R到M之间变化时，沉降A，B和C受到的影响都不大(见图12(b))。但从M向左移动到L时，沉降A受到影响很大，从14.88 mm增大到21.67 mm，增幅达到45.6%。沉降B和C受到桥台基础位置变化的影响有限，L情况下的沉降比M情况下的沉降量分别增加了14.2%和3.2%。

(a) 墙面侧向位移；(b) 沉降

(a) 墙面侧向位移；(b) 沉降

4.7 桥台基础荷载大小的影响

桥台基础荷载是加筋土桥台结构中加筋土挡墙承受的主要荷载。参数分析研究了0~200 kPa范围的桥台基础荷载下挡墙的变形。其下限和上限分别对应于在自重和较大桥梁车辆荷载的情况。由图13(a)可知，墙面侧向位移均随着桥台基础荷载水平的增大而显著增大，最大侧向位移从0 kPa时的7.13 mm增大到13.01 mm，增幅达82.4%。并且在荷载增大的过程中，中上部的侧向位移增加比下部位移更快，这种变化与墙脚受到水平约束作用有关。而沉降A，B和C几乎随着桥台基础荷载的增大而呈线性增加(图13(b))，其中沉降A点增加最为显著。200 kPa时A，B和C的沉降量分别为0 kPa时沉降的16.6倍、1.69倍和1.71倍。当桥台基础荷载较小(不超过50 kPa)时，沉降A很小，小于沉降B，然而当超过100 kPa以后，A的沉降量达到最大。

4.8 影响参数评价

表4总结了各研究参数对挡墙变形性能的影响。为了统一地评价这种影响，将每种参数在所研究范围内变化时引起的最大墙面侧向位移和桥台基础沉降(沉降A)进行正规化处理。将结果汇总到图14中，并假设4个范围来定义影响程度分类。

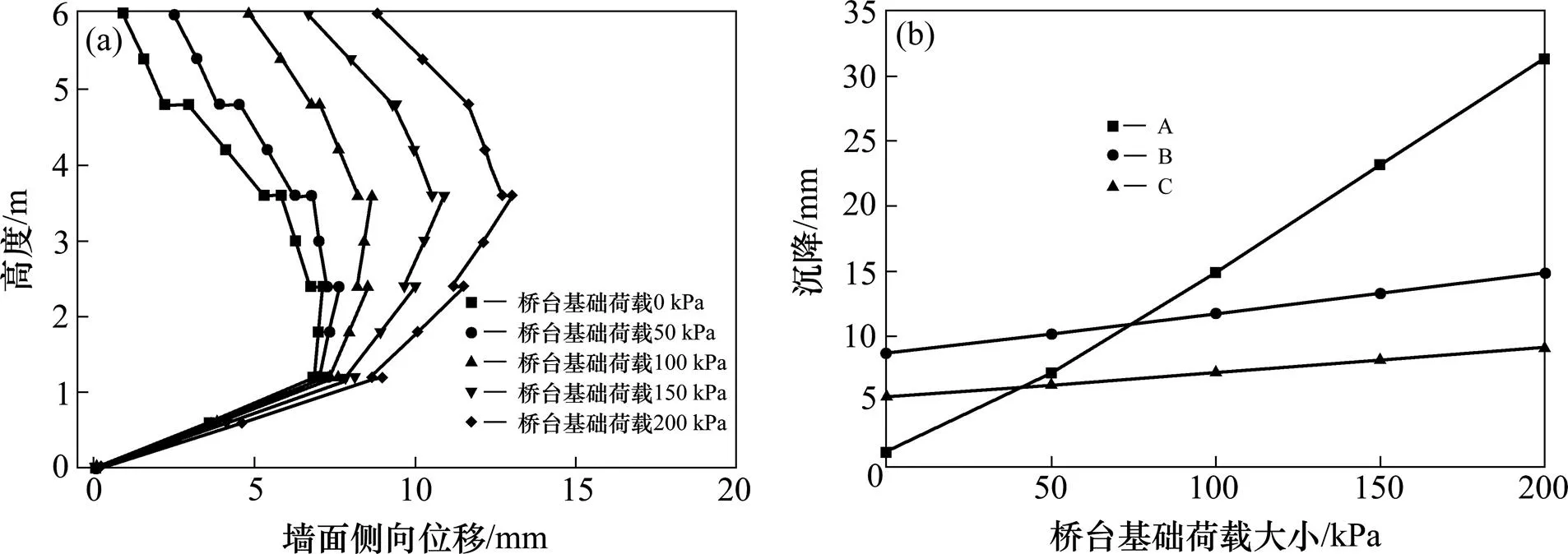
(a) 墙面侧向位移；(b) 沉降

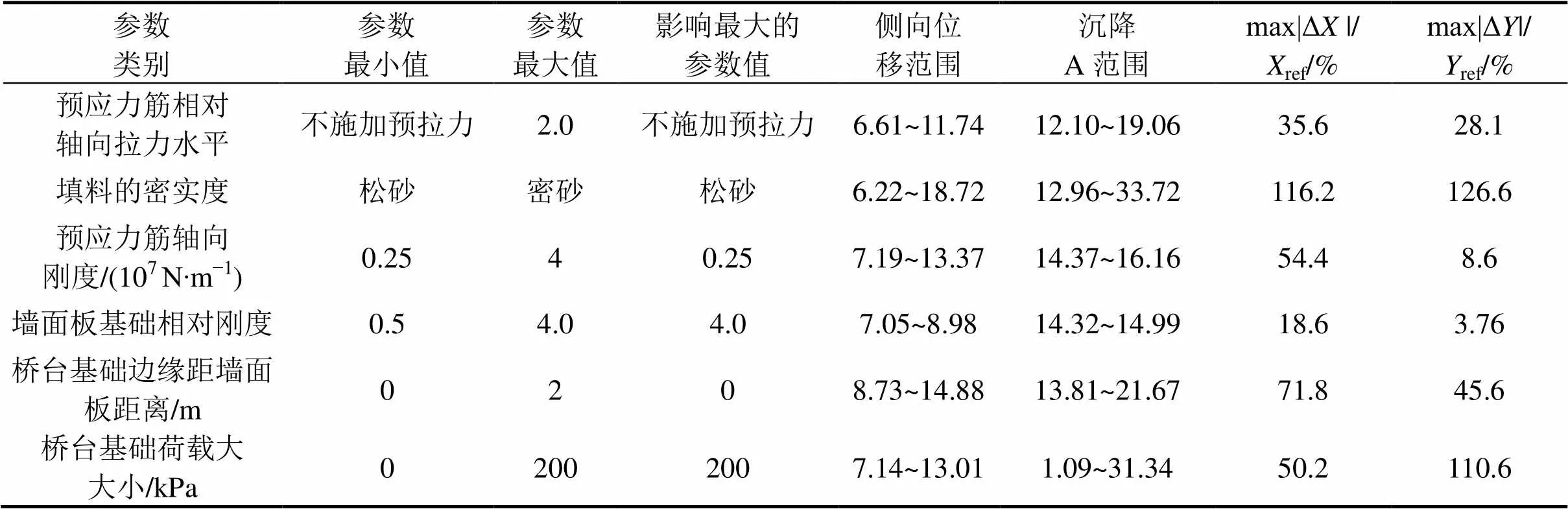
表4 各参数对挡墙变形的影响

注：max|Δ|/ref(%)和max|Δ|/ref(%)分别代表的是：将影响最大的参数值对应的墙面板最大侧向位移和桥台基础沉降分别利用基准工况的最大墙面侧向位移ref和桥台基础沉降ref进行正规化的结果。挡墙相对侧向位移Δ=ref与计算工况的最大侧向位移的差；桥台基础相对沉Δ=ref与计算工况的最大侧向位移的差，其中ref=8.66 mm，ref=14.88 mm

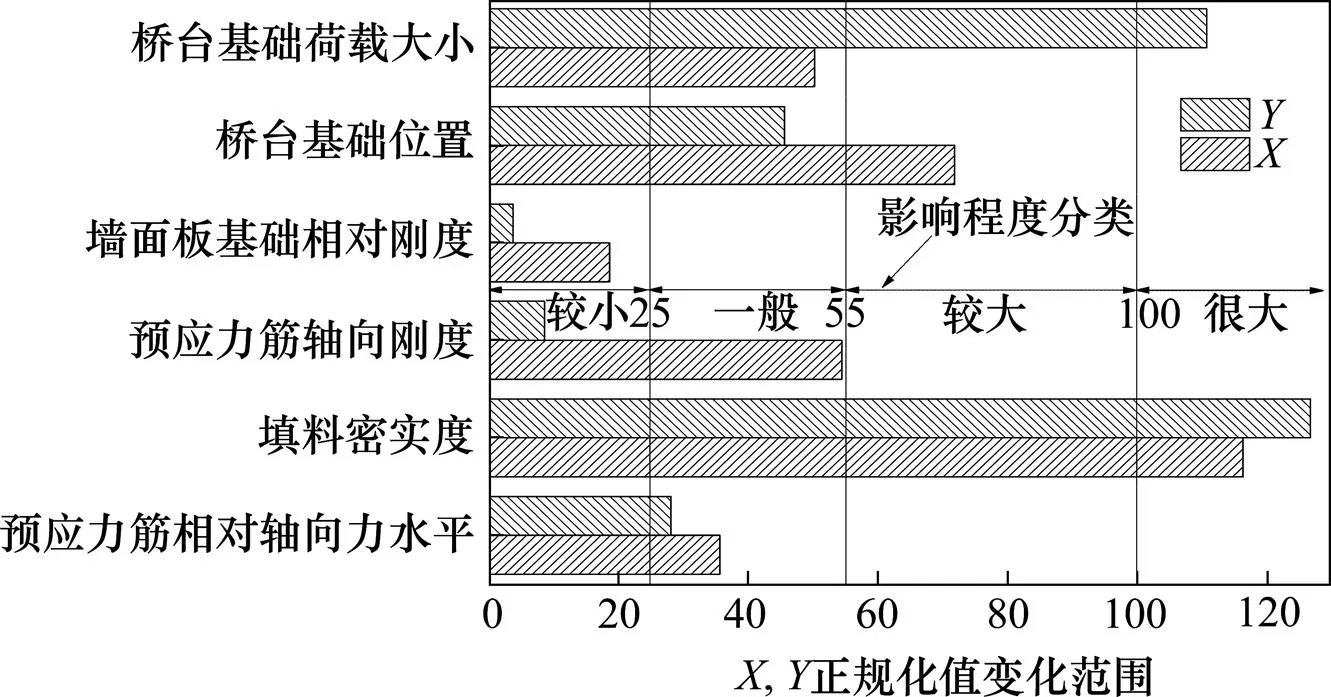
图14 影响最大参数值正规化结果

从图14可以看出，同一参数对墙面侧向位移和桥台基础沉降影响程度并不一定相同，预应力筋轴向刚度对墙面侧向位移的影响程度要显著大于对桥台基础沉降的影响。而桥台基础荷载大小对桥台基础沉降的影响程度则明显大于墙面侧向位移的影响程度。

总体来看，影响墙面板侧向位移最重要的2个因素是填料的密实度和桥台基础边缘距墙面板的距离。而影响桥台基础沉降的最主要的2个因素是填料的密实度和桥台基础的荷载大小。在所研究的参数范围内，墙面板基础刚度对挡墙侧向位移和桥台基础位置沉降的影响均较小。另外，预应力筋的相对轴向拉力水平对墙面侧向位移和桥台基础沉降均产生一定程度的影响。

以上参数分析结果说明，在桥台基础荷载一定的情况下，选择具有较高的密实度的填料，并避免桥台基础边缘过于靠近挡土墙墙面板，对于控制挡墙的变形具有重要意义。

5 结论

1) 预应力筋的预拉力能够提高加筋区整体性，在荷载作用下，预拉力的挡墙产生的侧向位移和顶部沉降都比未施加预拉力挡墙小。

2) 在100 kPa桥台基础荷载作用下，基准工况产生最大为8.66 mm的墙面侧向位移和14.88 mm的桥台基础沉降。

3) 同一参数对预应力加筋土挡墙墙面侧向位移和桥台基础沉降影响程度并不一定相同。

4) 在所研究的参数对象范围内，填料的密实度和桥台基础边缘距墙面板的距离对墙面侧向位移影响最大，而填料的密实度和桥台基础的荷载大小对桥台基础沉降影响最大。在桥台基础荷载一定的情况下，选择具有较高密实度的填料并增加桥台基础距墙面板边缘距离有助于控制挡墙的变形。另外，在不考虑预拉力损失的情况下，合理的提高预应力筋的轴向刚度也有利于减小挡墙在桥台基础荷载作用下的变形。

[1] 杜运兴, 周芬, 梁强. 双根无黏结预应力筋加筋体力学性能研究[J]. 长江科学院院报, 2017, 34(2): 45−51. DU Yunxing, ZHOU Fen, LIANG Qiang. Research on mechanical properties of double-bonded prestressed steel reinforcement[J]. Journal of Yangtze River Scientific Research Institute, 2017, 34(2): 45−51.

[2] 管飞. 基于HSS本构模型的软土超大型深基坑3D数值分析[J]. 岩土工程学报,2010, 32(增1): 177−180. GUAN Fei. 3D numerical analysis for a ultra-large deep excavation in soft clay based on HSS constitutive model[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(Suppl 1): 177−180.

[3] 沈珠江. 理论土力学[M]. 北京: 中国水利水电出版社, 2000. SHEN Zhujiang. Theoretical soil mechanics[M]. Beijing: China Water & Power Press, 2000.

[4] Ömer B. Numerical studies of anchored sheet pile wall behavior constructed in cut and fill conditions[J]. Computers & Geotechnics, 2010, 37(3): 399−407.

[5] Allen T M, Bathurst R J. Performance of an 11 m high block-faced geogrid wall designed using the K-stiffness method[J]. Canadian Geotechnical Journal, 2014, 51(1): 16−29.

[6] Allen T M, Bathurst R J. Design and performance of 6.3 m-high, block-faced geogrid wall designed using K-stiffness method[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2013, 140(2): 217−235.

[7] YU Y, Bathurst R J, Allen T M, et al. Physical and numerical modelling of a geogrid-reinforced incremental concrete panel retaining wall[J]. Canadian Geotechnical Journal, 2016, 53(12): 1883−1901.

[8] Itasca Consulting Group. FLAC: fast lagrangian analysis of continua, user’s guide[R]. Itasca Consulting Group, Inc., Minneapolis, USA. 2011.

[9] LIU X A, Bradford M A, Lee M S S. Behavior of high-strength friction-grip bolted shear connectors in sustainable composite beams[J]. Journal of Structural Engineering, 2015, 141(6): 1−12.

[10] Damians I P, Bathurst R J, Josa A, et al. Numerical study of the influence of foundation compressibility and reinforcement stiffness on the behavior of reinforced soil walls[J]. International Journal of Geotechnical Engineering, 2014, 8(3): 247−259.

[11] Abu-Hejleh N, Zornberg J G, WANG T, et al. Performance of geosynthetic-reinforced walls supporting the founders/ meadows bridge and approaching roadway structures report 2: assessment of the performance and design of the front GRS walls and recommendations for future GRS abutments[R]. Colorado: Colorado Department of Transportation, 2001.

[12] Alam J, Siddiquee S A. A parametric study of anchored earth wall by finite element method[J]. Ksce Journal of Civil Engineering, 2014, 18(7): 2034−2042.

[13] Konami T, Miura K, Misawa K, et al. Observational construction of the multi-step type multi-anchored reinforced soil retaining wall[C]// Slopes and Retaining Structures Under Seismic and Static Conditions, ASCE, 2014: 1−11.

Deformation performance of pre-stressed reinforced earth retaining wall

DU Yunxing, YUAN Lan, CHEN Shiwen, ZHOU Fen

(College of Civil Engineering, Hunan University, Changsha 410082, China)

The finite difference method was used to study the lateral deformation and settlement law of pre-stressed reinforced earth retaining walls. Backfill soil was simulated by Plastic Hardening (PH) model with a hyperbolic stress-strain relationship. The filling and compaction process was considered in the numerical simulations which were verified by the results of model tests. Analysis cases were established according to the backfill compactness, the distance from the abutment base edge to the wall panel and the axial stiffness of pre-stressed bar. Results show that the displacement of the wall panel and the top settlement of the prestressed retaining wall under surcharge load were significantly smaller than those without pretension. The backfill compactness and the distance from the abutment base edge to the wall panel have the greatest influence on the lateral displacement of the wall. Increasing the axial stiffness of prestressed bars is beneficial to reduce the deformation of the retaining wall.

model tests; numerical simulation; pre-tension; lateral displacement; settlement

10.19713/j.cnki.43−1423/u.2019.03.014

TU472.3+4

A

1672 − 7029(2019)03 − 0664 − 10

2018−04−09

国家自然科学基金资助项目(51378199)；长沙市科技计划重大专项资助项目(kq1703002，kq1804002)；湖南省自然科学基金资助项目(2018JJ2050)

杜运兴(1971−)，男，河南平顶山人，教授，博士，从事加筋土技术研究；E−mail：duyunxing@hnu.edu.cn

(编辑 涂鹏)