考虑岩土应变软化特性的开挖扰动诱发路堑边坡渐进性破坏机理分析

魏小楠

(贵州省交通规划勘察设计研究院股份有限公司， 贵州 贵阳 550081)

1 引言

已有边坡稳定性分析方法有强度折减有限元分析方法、极限平衡法、条分法等，这些方法均假定滑裂面整体达到临界状态，即建立在极限状态之上。而现有研究表明：边坡的破坏实际上是渐变的过程，传统边坡研究方法将边坡视为整体静态来进行研究的假设与实际不符。针对边坡渐进性破坏，刘忠玉等考虑土体的流变效应，通过推广不平衡推力法，提出了边坡渐进性破坏力学模型，进行了稳定性分析，并发现边坡安全系数随时间变化而逐渐减小；黄伟等针对雪峰山露天矿多滑面边坡特点，建立以极限平衡为基础的功能函数和模糊可靠度算法，并对边坡进行稳定性分析；宋东日等针对山区牵引式滑坡，提出3种具体的边坡破坏机制，并对加固措施进行了探讨；肖超等对开挖与降雨作用下的边坡失稳机理进行了分析，表明边坡的破坏是一个渐进性破坏过程，雨水入渗是深层滑动面的诱发因素；张平等从裂隙岩石破坏渐进性过程以及破坏机制出发，提出渐进性破坏模式理论公式，并对已建立的渐进破损模型进行了试验验证；王庚荪提出了新的接触单元，模拟边坡的渐进性破坏过程并进行稳定性分析，表明考虑渐进性破坏过程求得的稳定性系数比不考虑渐进性破坏过程的有限元分析所得安全系数要小5%～10%。在此基础上，王庚荪等提出含剪切带单元模型，模拟了渐进性破坏过程并进行参数分析，表明岩土体的强度参数对滑动面形迹影响较小，但对安全系数影响较大。

该文以贵州某开挖路堑高边坡为工程背景，针对其易发生累进式的牵引滑动变形特点，综合考虑岩土体材料的应变软化特性，基于数值分析软件模拟边坡由于坡脚开挖诱发的渐进性失稳过程。并对坡脚开挖诱发超高路堑边坡失稳进行失稳特性分析，研究边坡安全系数在坡脚开挖诱发的边坡失稳过程中的变化规律。

2 工程背景

某路堑边坡，地层为上覆第四系残坡积层含碎石粉质黏土及碎石土。下伏基岩为二叠系龙潭组砂岩、泥岩、夹层煤；二叠系飞仙关组粉砂质泥岩、间夹一层灰岩。原设计为4级边坡，最大挖高38.5 m，轴线最大挖高28.9 m，边坡开挖至第2级坡面时，在2、3级坡中部出现蠕滑剪出的裂缝，同时坡口外出现裂缝。边坡出现蠕滑变形后，对坡面防护设计进行调整，放缓边坡进行清方减载，原4级边坡变为5级坡。第1级边坡抗滑桩在挖孔过程中出现塌孔，最远处裂缝距离第5级边坡坡顶120 m。第3级边坡拱形骨架出现了坍塌，整段边坡向路基方向滑移。该路堑边坡断面及地层岩性如图1所示。

图1 路堑边坡横断面及地层岩性

3 坡脚开挖诱发路堑边坡失稳特性分析

3.1 开挖施工诱发滑坡破坏稳定性分析

考虑到该依托工程边坡变形稳定特性与坡角分级开挖施工密切相关，在开挖坡角台阶边坡的各个阶段均表现出了不同的稳定状态，此处首先基于传统稳定性分析原理，对坡脚分级开挖过程中的边坡稳定性动态变化进行研究；即假定岩土体抗剪强度特征未受应变软化特性影响，分析与之对应的分级开挖施工条件下的边坡安全系数。采用FLAC3D内嵌强度折减法对分级开挖边坡进行稳定性分析，得到边坡安全系数与开挖边坡级数见图2。

图2 安全系数随开挖级数变化

从图2中可以看出：① 未考虑岩土体材料应变软化特性条件下，边坡安全系数随开挖级数的增大而不断减小；② 传统强度折减技术均假定开挖过程为静态过程，获求的是边坡每一施工工序最终的安全系数特性，且岩土材料强度特性维持不变，这与依托工点边坡蠕滑特性不一致。因此有必要进一步引入岩土材料应变软化特性进行边坡渐进性失稳特性分析。

3.2 岩土体渐进式破坏力学特性分析

高路堑边坡失稳主要是因为随着开挖量的增加，坡脚关键阻滑块体缺失，诱发坡体开挖应力释放，土应力急剧调整，岩土体屈服变形，边坡稳定性降低。当塑性区逐渐衍生至完全贯通时，边坡整体失稳。已有文献表明：岩土体渐进式破坏主要表现在空间位置上滑裂面的参数劣变是逐步产生发展的，滑面上各位置的参数存在差异性以及时间上滑裂面上强度参数随渐进演化发展呈现不同的速率劣变。

4 考虑岩土应变软化特性的路堑边坡渐进性破坏机理

4.1 岩土应变软化特性分析

边坡破坏过程实质上是滑裂面上强度参数劣变过程。FLAC3D内嵌应变软化模型实质上是摩尔-库仑屈服准则中强度参数与相应软化应变参数建立的函数关系。

摩尔-库仑强度准则：

(1)

式中：σ1、σ2、σ3为3个主应力，且σ1≤σ2≤σ3。

屈服函数：

(2)

ft=σ3-σt=0

(3)

对于坡体来说，剪切与拉伸势函数如下：

(4)

gt=-σ3

(5)

式中：ψ为剪胀角。

在应变软化模型中，强度参数与软化参数(图3)之间的关系表达式如下：

(6)

(7)

式中：cp为峰值黏聚力；cr为残余黏聚力；φp为峰值内摩擦角；φr为残余内摩擦角；ηp为峰后软化开始时的软化参数；ηr为软化结束进入残余阶段时的软化参数。

等效塑性剪应变增量：

(8)

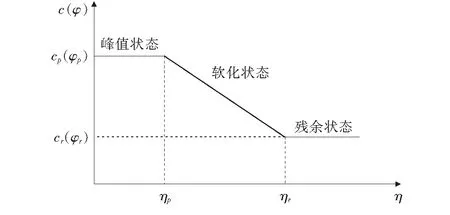
图3 强度参数变化示意图

4.2 路堑边坡渐进性破坏机理分析

4.2.1 岩土材料特性及数值建模

为保证该文数值建模的合理以及可靠性，首先通过Auto CAD输出的图形交互文件，导入Midas建立对应的边坡网格模型。再通过Midas_to_FLAC3D接口程序，生成FLAC3D模型。模型边界为左、右侧面边界采用水平约束，底面边界采用水平、垂直全约束。

根据边坡数值建模与实际边坡各开挖阶段边坡破坏特征与安全系数一致性要求，基于滑坡极限状态分析以及滑裂面位置，对背景工程坡体强度参数进行反演分析。参考相关文献，该节选取设计报告中的强度参数，综合确定了各岩土层物理力学参数如表1所示。

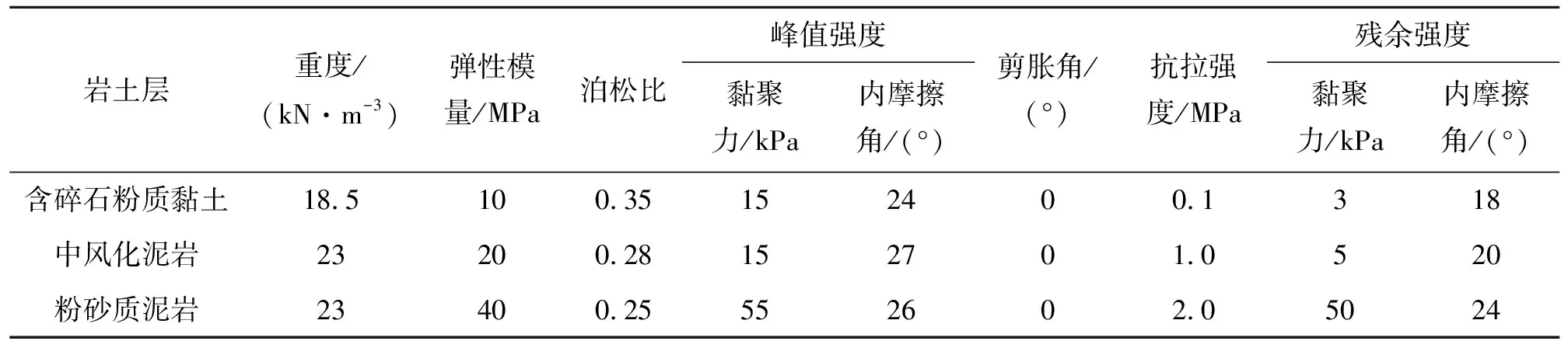
表1 计算模型参数取值

4.2.2 路堑边坡渐进性破坏数值分析

路堑高边坡渐进性破坏时由于坡脚开挖，致使开挖应力释放，岩土体应力状态重新调整，产生塑性屈服、应变累积以及卸荷松动，边坡稳定状态降低，当塑性区延伸扩展至贯通时，边坡失稳。利用FLAC3D内嵌应变软化模型，对原始坡体以及5次刷坡坡体分别进行了模拟分析，得到其塑性区演变过程。

从演变过程可知：边坡开挖初期(第1、2次刷坡)，即边坡上端的坡体少量开挖，对天然稳定状态的斜坡应力状态改变较小，边坡整体仍能维持平衡，土体中未形成塑性区。随着开挖量的增加，坡脚出现应力集中，坡脚处出现塑性屈服，塑性区随着开挖量的增加不断向上延伸。当边坡临近极限状态时，即进行第5次刷坡时，塑性区迅速贯通，边坡整体失稳。

图4为第5次刷坡考虑应变软化的边坡塑性区随开挖时步的变化图，在软化初期，坡脚处出现张拉屈服以及剪切屈服，随着时步的增大，剪切塑性区不断延伸，坡顶以及坡体表面出现张拉屈服，坡体表面产生裂缝，这也与背景工程整体失稳时的裂缝出现位置相符。

图5～7为考虑应变软化第5次刷坡时剪应变增量、滑裂面强度参数黏聚力以及内摩擦角随时步的变化。从图5～7可以看出：边坡的破坏其实质上是由于滑裂面上强度参数的劣变，且参数的劣变发展规律与剪应变增量的延伸规律一致，表明参数劣化与该处的剪应变增量相关。

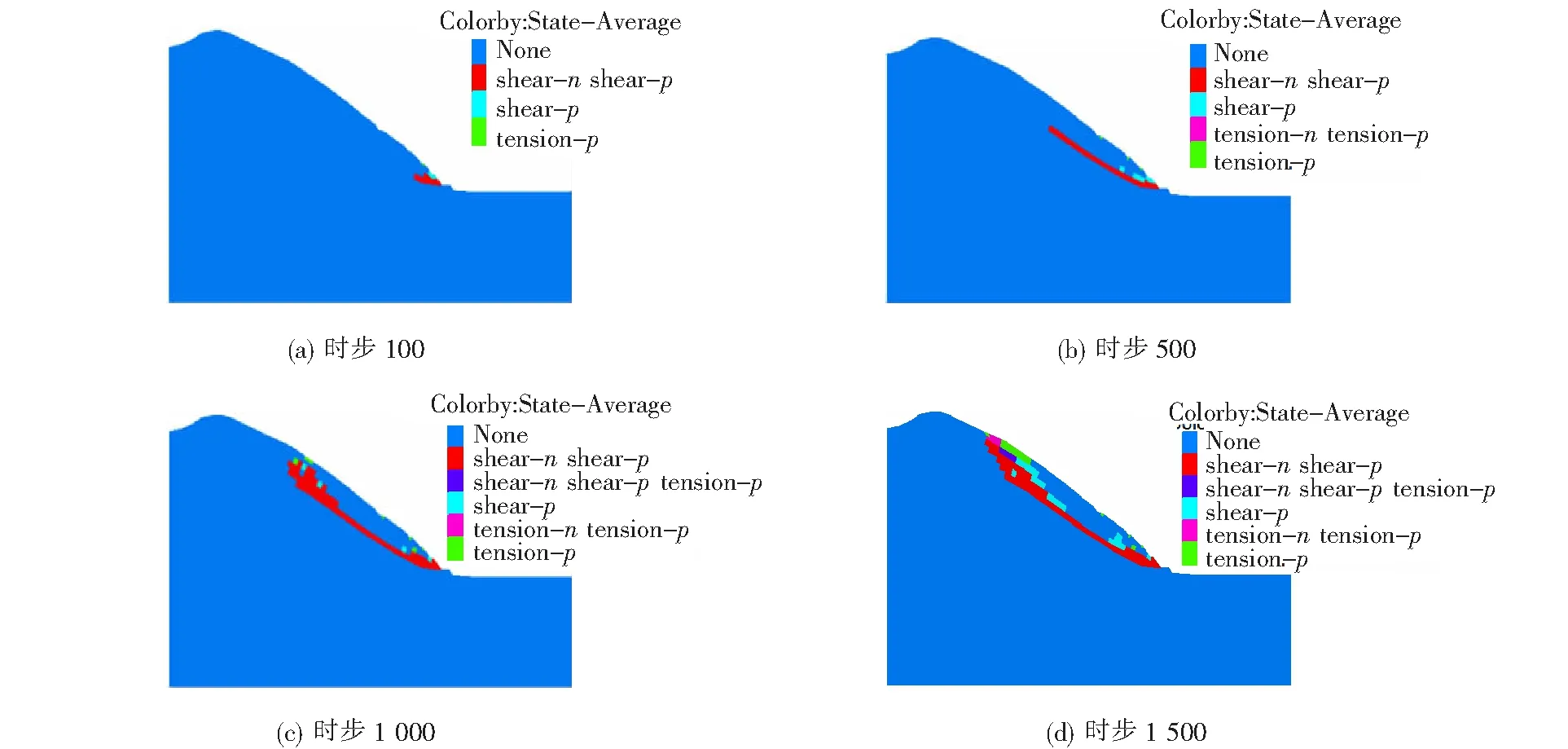
图4 塑性区随开挖时步变化

图5 剪应变增量随开挖时步变化

图6 黏聚力值随开挖时步变化(单位：kPa)

图7 内摩擦角值随开挖时步变化[单位：(°)]

5 结论

基于边坡渐进性破坏的特点，考虑破坏时滑动面上强度参数的应变软化特性，基于FLAC3D有限差分软件平台，分析坡脚开挖诱发的高路堑边坡的渐进性破坏过程。得出以下结论：

(1) 高路堑边坡的破坏是由于边坡坡脚开挖，导致坡脚阻滑块体缺失，其实质是由于滑裂面强度参数的劣变。

(2) 边坡的失稳是由局部变形累积、延伸直至贯通的整体破坏渐进过程，在此渐进性发展过程中，滑裂面上强度参数的折减速率与剪应变增量有关。

(3) 随着开挖级数增大，边坡稳定状态降低。边坡渐进性破坏的各阶段具有不同的稳定状态和安全系数。