考虑公路等级的沥青路面性能衰变预测方法

周育名， 李金明， 李平， 陈致远， 段筱娟

(1.长沙理工大学 交通运输工程学院， 湖南 长沙 410114; 2.中国公路工程咨询集团有限公司)

1 前言

近年来，中国公路建设取得了飞速发展，截至2017年底，中国公路总里程为477.35万km，养护里程467.66万km，占总里程的97.9%。伴随着公路大规模建设接近尾声，公路的养护与管理越来越得到了人们的重视。交通运输部“十二五”公路养护管理发展规划提出，在“十二五”期间要基本建立国省道及高速养护管理科学决策体系，这期中关键的一步就是路面使用性能的预测，科学决策是建立在准确预测路面性能的基础上，没有准确的性能预测，决策往往会造成养护资金的浪费、路面使用质量下降及使用费用上升等现象。 对沥青路面使用性能的预测，国内外进行了大量的研究。美国公路与运输协会在1993年出版的AASHTO设计指南中以路面现时服务能力指数PSI(Present Serviceability Index)作为评价路面性能的重要指标，并提出PSI与交通轴载作用次数的函数关系；MS Sakhaeifar、M Karaahin、Yang J D先后采用神经网络、模糊逻辑、马尔可夫矩阵方法对路面衰变性能进行了研究；Hofko B在室内对沥青混合料永久变形进行了预测研究；Gharaibeh将路面性能衰变模型应用于路面养护管理系统；Chris Raymond对加拿大路面性能衰减模型进行了研究。中国的一些专家学者们针对中国的国情，对中国沥青路面使用性能衰变规律也进行了相关研究，最早开始路面性能衰减模型研究的是刘伯莹、孙立军等；王春红采用指数形模型对路面预防性养护进行了研究；张占军、王笑风采用修正的双参数模型对路面长期性能进行了研究；王朝辉、武建民分别采用数据包络分析和时间序列分析法对路面性能进行了预测；张金喜、范灵雨对采用时间为自变量对指数形衰减模型进行了研究；肖金平通过对湖南省高速公路沥青路面使用性能衰变的研究，提出了余弦函数预测模型。在确定型模型研究较为成熟后，近年来，概率型模型研究也逐渐兴起，王艳丽、傅东阳等、王国晓等分别采用人工神经网络、马尔可夫模型、灰色理论对沥青路面衰变性能进行了研究。在确定型模型研究中，目前更多的预测模型自变量对应的是时间，多是以年为单位，导致交通量轴载对路面性能指标衰减的影响并不能完全体现出来，虽然在模型回归的过程中，回归出的参数能部分体现交通量轴载的影响，但这远远不够，成为了目前路面性能衰变模型研究过程中的一大缺陷。此外，路面性能衰变模型与路面类型、结构层厚度、基层类型、土基状况、路面材料等内在因素均具有一定的关系，但目前这些模型中，均以一个整体模型代表了路面性能的衰变规律，其他内在因素均在模型回归参数中体现，导致不同路面的性能预测值与实际值相差甚远，对未来决策无指导意义，甚至误导决策者的决策行为。

该文旨在通过对既有路面性能衰变模型的分析，实地交通量、轴重及路况数据收集，筛选出影响路面性能衰减的主要因素，对以时间和累计当量轴次为自变量的性能预测模型进行对比分析，然后研究不同面层厚度条件下4种衰变模型曲线，最终建立半刚性基层沥青路面不同面层厚度、基层厚度条件下以累计轴载作用次数为主要自变量的沥青路面性能衰变方程。

2 路面性能衰变规律

路面性能衰变是指路面在行车荷载、环境因素和时间的综合作用下所特有的使用性能变化规律。目前其主要形式有图1所示的4种。

图1 路面性能衰变曲线

图1中4条曲线代表4种不同的衰变速度，其共同特点是：随着使用时间或荷载作用次数的增加，使用性能呈下降趋势，即路况在不断恶化，所能提供的服务能力日益衰减，只是4种曲线反映的衰变过程有快有慢。在确定型路面性能预测模型中，目前主要有直线形、S形、指数形、多项式形4种，每种模型均有其优缺点，4种模型对比见表1。

表1 不同函数形式的衰变方程对比

3 路面性能衰变影响因素分析

影响路面使用性能的因素繁多，这些因素的差异性和不稳定性使得路面状况的变化复杂多样，千差万别。影响使用性能的因素有：交通荷载、环境状况、施工和养护水平等外在因素；路面结构组合与厚度、基层类型、结构强度、土基状况、路面材料等内在因素。但鉴于目前研究技术的局限性，还未将上述因素全部定量地考虑到模型方程中。该文主要对影响路面性能衰变的主要因素进行分析。

(1) 面层类型

路面的面层类型包括沥青路面、水泥路面和砂石路面，不同的面层类型，其性能衰减曲线有所不同。该文针对某省国省干线历年检测数据，其90%以上均为沥青路面，因此，只针对沥青路面进行研究。

(2) 面层厚度

面层厚度较薄时，使用性能下降速率较大，随着面层厚度的增加，结构承载能力增强，路面有能力承受较大的破坏力，不至于很快损坏，能在较长时期内保持良好的行车舒适性。所以，随着面层厚度的增加，同样行车荷载的作用下，性能衰变由快到慢。该文针对某省国省干线，经统计分析，面层厚度主要为0～5、5～10和15～20 cm3种，其中0～5 cm代表三级、四级公路，5～10 cm代表二级、一级公路，15～20 cm代表高速公路。

(3) 基层类型

分为半刚性基层、柔性基层和刚性基层，这3类基层的强度相差较大，其路面在相同的荷载条件下，损坏情况相差较大。而以同一类基层中的不同材料为基层的路段，损坏状况则没有明显的差别。目前中国应用最多的基层类型为半刚性基层，为了收集更多的数据，该文只考虑半刚性基层。

(4) 基层厚度

不同半刚性基层厚度的沥青路面衰减速率不一，一般规律是基层越薄，衰减速率越大。该文结合面层厚度分类方法，将半刚性基层厚度分为15～25、25～35和35～45 cm3种，其中15～25 cm主要代表三级、四级公路，25～35 cm主要代表二级、一级公路，35～45 cm主要代表高速公路。

(5) 路龄

路龄是指公路建成通车年限，通常按年来预测路面性能，但由于不同公路的实际交通量及组成差别可能会很大，例如一条道路平均交通量为10 000 pcu/d，另一条为3 000 pcu/d，会导致随着路龄的增加，两条道路的路面性能差别越来越大；此外如果两条道路平均交通量均为10 000 pcu/d，但车辆组成差别较大，一条以小客车为主，另一条以大货车为主，同样会出现上述问题。因此，以时间为自变量预测路面性能存在一定的缺陷。

该文将时间转换为累计当量轴次，这样同时解决了不同道路交通量大小和交通量组成对路面性能衰减的影响，也与路面厚度设计时采用的未来年限累计当量轴载次数相呼应。为了对比分析，分别采用年和累计轴载次数作为自变量进行路面性能衰减预测。

4 路面性能衰变模型建立

综上所述，针对某省国省干线半刚性基层沥青路面性能衰减规律进行研究，根据2011—2014年不同路段的检测数据，其中高速公路路段共44个、一、二级公路路段34个，三、四级公路路段27个。对比不同面层厚度、不同基层厚度、不同模型形式、不同自变量时路面性能衰减曲线的变化，具体见表2。

表2 不同代表公路等级计算模式

4.1 高速公路

通过对2011—2014年部分高速公路路段检测数据的收集，分别以时间(年)和累计当量轴载次数为自变量，路面PCI为纵坐标进行回归分析，回归结果见表3，性能衰减变化图见图2。

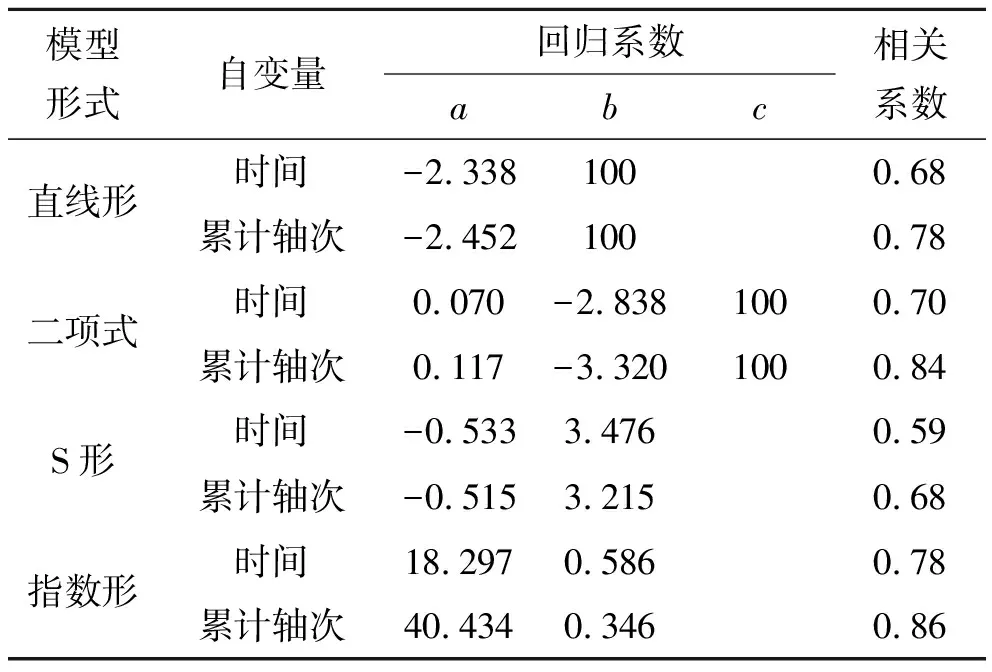
表3 不同模型形式及自变量的回归系数和相关系数

对比表3和图2，分析可知：

(1) 4种模型中以指数形相关性最好，最高为0.86，S形相关性最差，最低为0.59。究其原因是由于S形模型后期性能衰减较慢，但高速公路的路面性能一般较高，养护资金也较为充足，当路面性能降低到一定水平后，就已经进行了相关的养护，使其路面性能提高到原来的水平。

图2 不同模型性能衰减图(高速公路)

(2) 4种模型中采用累计当量轴次为自变量的相关系数均高于采用时间为自变量的相关系数，提高0.08～0.14，平均提高0.1。

(3) 无论采用何种模型，高速公路的相关系数均相对较高，分析原因：① 与高速公路施工过程中的规范性有一定的关系，包括原材料选择、施工过程控制等环节；② 与数据采集的准确性有关。

4.2 一、二级公路

通过对2011—2014年部分一级公路、二级公路路段检测数据的收集，分别以时间和累计当量轴载次数为自变量，路面PCI为纵坐标进行回归分析，结果见表4，性能衰减变化见图3。

对比表4和图3，分析可知：

(1) 4种模型中以S形相关性最好，最高为0.83，直线形和二项式相关性最差，最低为0.51。

(2) 4种模型中采用累计当量轴次为自变量的相关系数均高于采用时间为自变量的相关系数，提高0.21～0.31，平均提高0.28。

(3) 一、二级公路的回归系数较高速公路低，其施工水平、养护水平较高速公路差，且其各条公路交通量

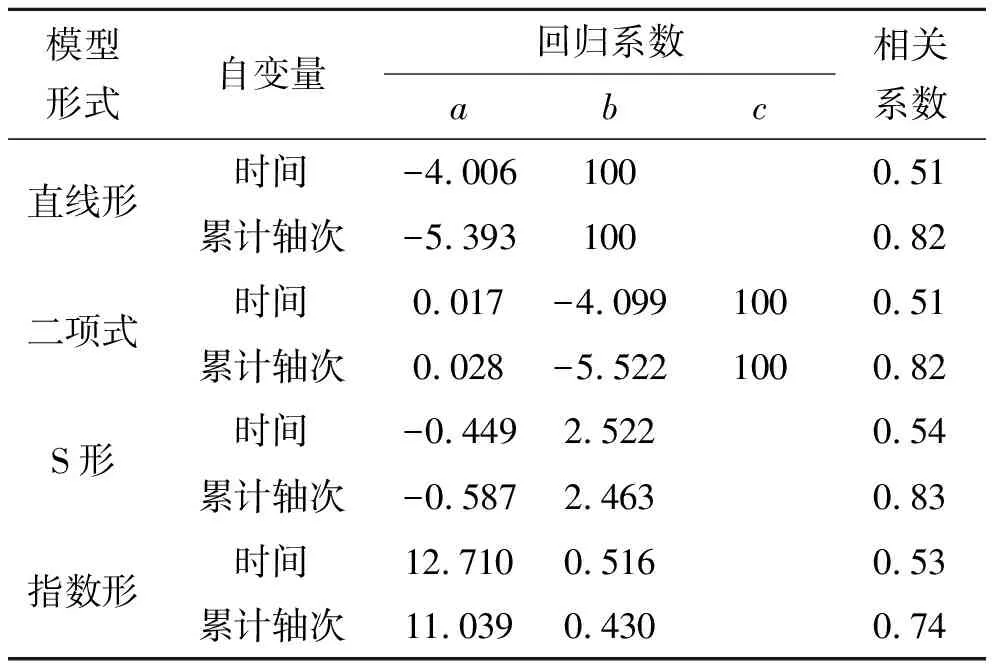
表4 不同模型形式及自变量的回归系数和相关系数

图3 不同模型性能衰减图(一、二级公路)

差别很大，交通量较小的路段每天不足千辆，交通量较大的路段接近万辆，且重车较多，导致同样使用年限的路面，其病害发展速度相差很大，这也正是采用年为自变量回归的模型相关系数低，而采用累计当量轴次为自变量回归的模型相关系数高的原因。

4.3 三、四级公路

通过对2011—2014年部分三级、四级公路路段检测数据收集，分别以年和累计当量轴载次数为自变量，路面PCI为纵坐标进行回归分析，结果见表5，性能衰减变化见图4。

对比表5和图4，分析可知：

(1) 4种模型中以S形相关性最好，最高为0.69，直线形相关性最差，最低为0.34。

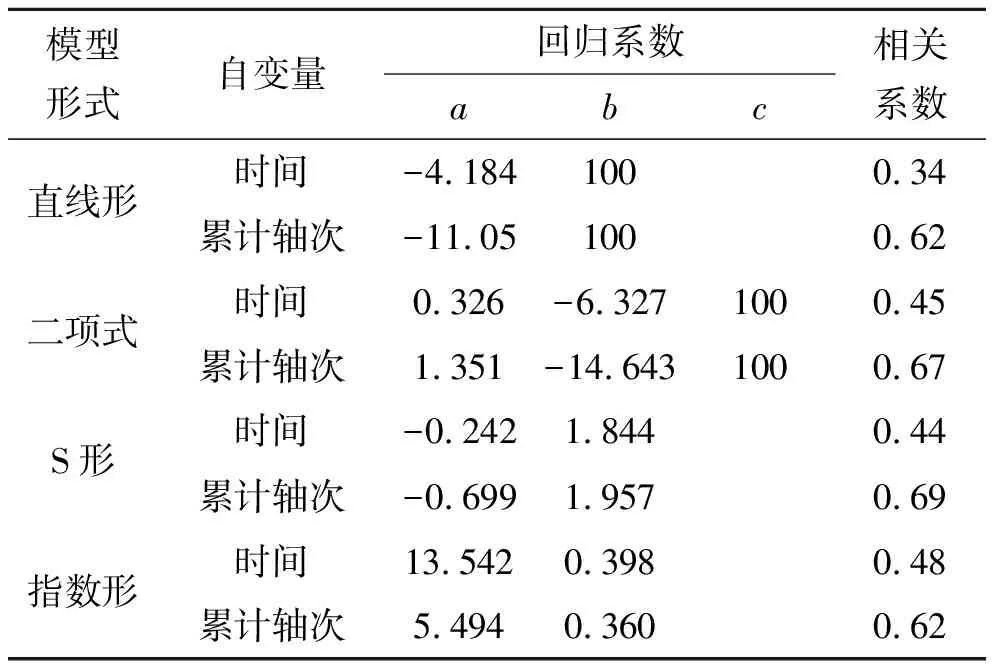
表5 不同模型形式及自变量的回归系数和相关系数

图4 不同模型性能衰减图(三、四级公路)

(2) 4种模型中采用累计当量轴次为自变量的相关系数均高于采用时间为自变量的相关系数，提高0.14～0.28，平均提高0.22。

(3) 无论采用何种模型，三级公路、四级公路的相关系数均较低，分析原因：① 低等级公路施工过程中相对不规范；② 路面检测数据采集准确性不高；③ 交通量及组成调查数据准确度欠佳。

5 性能预测

采用上述回归方法中相关系数最高的模型进行2015年路况性能指标的预测，并与2015年实际检测数据进行对比，将所有的路段结果值进行平均，见表6。

表6 模型预测与实际值对比

由表6可知：不管是指数形，还是S形模型，采用累计当量轴次为自变量时，其PCI预测值与实际值都更为接近，具体到每个路段的实际差别见图5。

图5 性能预测值与实际路况值差别百分比分布

由图5可知：以年为自变量时，高速公路的预测结果要好，其他等级公路较差，部分路段的预测值与实际值的差别甚至超过了10%。当以累计当量轴次为自变量时，总体效果均较好，虽然存在预测值与实际值差别大于5%的路段，但数量极少，且绝大多数路段预测值与实际值的差别均小于3%。

6 结论

通过对某省国省干线2011—2014年沥青路面检测数据的分析，通过建立不同的预测模型，并与实际检测结果进行了对比分析，得出如下结论：

(1) 累计当量轴次是路面性能衰减最为主要的影响因素，对于交通量差别较大的路面性能预测而言，采用累计当量轴次建立的路面衰减性能模型较采用时间建立的模型更为准确。分析表明：高速公路的相关系数能提高约0.1；一、二公路的相关系数能提高约0.28；三、四公路的相关系数能提高约0.22。

(2) 进行“十三五”路面养护规划过程中，针对高速公路路面性能预测，推荐采用累计当量轴次为自变量的指数形模型进行预测；对于其他等级公路的路面性能，推荐采用累计当量轴次为自变量的S形模型进行预测。能更加准确地预测未来路面发展状况，以便采取针对性的养护措施和进行准确的资金预算。

(3) 影响路面使用性能衰减的因素也包含了气候环境、施工水平等，如何将诸多因素综合考虑在性能衰减模型中，是下一步研究的重点。