桥塔约束刚度对单跨双缆悬索桥受力特性的影响

冯国瀚，陈进昌，雷俊卿*

(1.北京交通大学 土木建筑工程学院，北京市 100044；2.中铁工程设计咨询集团有限公司)

目前已建成的悬索桥以单跨悬索桥居多，而随着跨度的增大，再增大单跨悬索桥的跨径从设计和施工方面来说，都不是特别的经济。特别对于宽水面的江河和海域，多塔悬索桥就凸显出特有的优势。但是多塔悬索桥也有致命的缺点，就是由于中间塔没有边锚索的有效约束，在荷载作用下，整个结构会有较大的变形。增加中间桥塔的刚度可以减小这种结构变形，但是会使桥塔的底部承受巨大的弯矩与剪力，所以这种方法并不可取。由于传统悬索桥的这个缺点，一些研究者就从改变悬索桥的结构入手，提出了双缆悬索桥这种新型结构，并进行了基本的力学分析，说明了双缆悬索桥的合理性。柴生波等通过数学推导及有限元模拟详细分析了单跨及多跨双缆悬索桥的力学特性，研究表明：相比于传统的多塔悬索桥，双缆多塔悬索桥在承受不平衡力时，塔顶位移及跨中挠度明显减小。虽然有很多学者都研究了双缆悬索桥的力学特性，但是他们在研究单跨双缆悬索桥时，将主塔塔顶作为约束处理，并没有考虑桥塔的约束刚度，该文考虑桥塔约束刚度对单跨双缆悬索桥的受力特性，并推导相关理论公式，分析力学特性的本质。

1 双缆悬索桥结构特点

与传统悬索桥不同的是双缆悬索桥有两根主缆，而且主缆的垂跨比不同，如图1所示，因此在受力时与传统悬索桥存在区别，双缆悬索桥通过协调变形调节力在两根主缆的分配比例。

图1 单跨双缆悬索桥示意图

文献[8]详细推导了双缆悬索桥在承受均布恒载的情况下，吊索内力分配比值的理论计算公式，并探究了其力学特性，研究表明：单跨双缆悬索桥在承受集中力作用时变形特性与传统的悬索桥类似，竖向刚度相比于传统悬索桥也没有明显的提高。但是当多塔悬索桥采用双缆时，双缆悬索桥的优势就被体现出来。柴生波等学者就提出等效虚拟缆的概念来研究多塔双缆悬索桥的力学特征。传统的多塔悬索桥在承受不平衡活载时，需要通过主缆发生较大的变形来平衡，而双缆悬索桥则是通过改变水平力在上下主缆的分配比例来平衡这种力，所以双缆悬索桥就具有较大的竖向刚度和抵抗变形的能力。

文献[8]在推导双缆悬索桥吊索内力分配比值的理论计算公式时，假设桥塔的塔顶是固定约束不可移动的，在成桥时这种假设是正确的，因为成桥时所有点的位置都要到达指定的坐标，也就相当于在均布恒载作用下，塔顶顺桥向位移为0。此时可以采用此公式求出各主缆承受力的大小，然后将双缆悬索桥看成两根单缆悬索桥来求成桥的初始状态，继而进行非线性分析，这是一个非常好的计算公式。但是当双缆悬索桥在承受活载时，桥塔塔顶并非不动，所以就不能将桥塔塔顶看成约束点来处理，而要考虑它的刚度。悬索桥在成桥后，主要是承受各种活载，尤其对于承受活载较大的铁路桥梁，严谨地分析出活载在上下缆之间的分配原则对桥梁设计及优化都是必要的。

2 单跨双缆悬索桥计算理论

在悬索桥作用均布荷载时，需要分析出均布荷载在上缆和下缆之间的分配关系，这样才能进行结构分析，所以推导出荷载在上缆和下缆之间的分配关系影响因素和相关公式非常必要。

2.1 基本假设

(1)假设活载均布加载到加劲梁上，即认为下吊索的每根吊索上的力相同，上吊索每根吊索上的力相同。

(2)不考虑吊索的弹性伸长，即认为每根吊索的顶端和底端的位移相同。

(3)考虑悬索桥塔顶的纵桥向位移，不考虑竖向位移，竖向位移认为是0。

计算图式如图2所示。

图2 双缆悬索桥理论计算图

图2中，H1为上主缆的水平张力；H2为下主缆的水平张力；f1为上缆的垂度；f2为下缆的垂度；k为桥塔的约束刚度；L为单跨悬索桥主跨的跨度；S1为主跨上缆的索长；S2为主跨下缆的索长。

2.2 理论公式推导

悬索桥主缆长度S可通过垂跨比n和跨径L得到：

(1)

式(1)中垂跨比n=f/L,考虑主塔顶的纵向位移，即认为L不是定值，对式(1)求导：

(2)

为了方便后面公式的书写，在这里用字母a和b来替代上面复杂的代数式，即：

(3)

(4)

因此式(2)简写为：

dS=adL+bLdn

(5)

主缆的应变ε为：

(6)

主缆的应变ε同样可以近似等于：

(7)

式中：H为主缆的水平力；E为主缆的弹性模量；A为主缆的截面面积，如果主缆的垂度为f,作用在主缆和吊索节点位置的竖向力为q,则有以下关系：

(8)

联立式(6)、(7)和(8)可以得到：

(9)

初始假设考虑的是主塔的约束刚度，所以在这里设主塔的约束刚度为k(包含边缆对主塔的约束作用),但因为单跨悬索桥的跨度是在减小的，而且主塔顶端都在向跨中移动，所以：

(10)

对于双缆悬索桥，H=H1+H2,即总的水平力是上下两根主缆的水平力之和，需要用式(8)分别求得，综合式(8)、(9)和(10)，可以分别得到上缆和下缆垂跨比的改变量dn1和dn2：

(11)

(12)

式中：q2为下吊索的内力；q1为上吊索的内力，记为：

(13)

(14)

上式中a和b参考公式(3)和(4)，而公式(11)和(12)就可以简写为：

dn1=C1q1+D1(q2-q1)

(15)

dn2=C2(q2-q1)+D2q1

(16)

从式(15)、(16)可以发现，两根主缆的垂跨比改变量dn与两根主缆的受力有关，不是独立的。系数C1为上缆受到的吊索力q1对垂跨比改变量dn1的影响；D1为下缆受到的吊索合力(q2-q1)对上缆垂跨比的改变量dn1的影响，主要体现在下缆受力改变了塔顶的位移，从而影响上缆垂跨比的改变量，这是非常符合实际情况的。

忽略吊杆的伸长量，故可认为dn1=dn2,那么联立公式(15)和(16)，即可得到下吊索的索力q2与上吊索索力q1的比值：

(17)

式(17)为单跨双缆悬索桥在承受满跨均布荷载时上吊索和下吊索内力的比值，反映其在上缆和下缆之间的分配关系，C1、C2、D1、D2由式(13)、(14)得到。

3 有限元模型计算分析

3.1 模型结构及尺寸

为了验证理论计算公式的正确性，用Midas建立二维有限元模型，双缆悬索桥结构尺寸如图3所示。

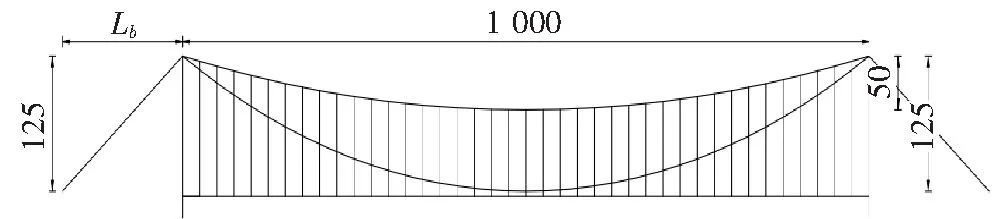
图3 双缆悬索桥结构尺寸(单位：m)

图3中Lb为变量，在模型中通过改变Lb的值来改变桥塔的约束刚度k。悬索桥的主跨为1 000 m，上缆的垂度为50 m,下缆的垂度为125 m，吊索的间距为25 m，桥塔高度h=150 m,加劲梁每延米重量为279.5 kN,构件的相关参数如表1所示。

3.2 计算结果及误差分析

桥塔的约束刚度k由主塔的抗弯刚度和边缆提供，所以改变锚碇到主塔的距离Lb,就可以改变桥塔的约束刚度。表2、3为不同的约束刚度k下，作用5 kN/m的均布荷载，模型下、上吊索内力比值的平均值和模型下、上主缆内力比值的平均值，以及采用式(17)、(8)计算得出的相应结果对比。

表1 双缆悬索桥材料特性

表2 吊索内力比值的理论与模型计算结果对比

注：①q1为上吊索内力，q2为下吊索内力；② 相对误差=|理论结果-模型结果|/理论结果×100%，下同。

采用式(8)计算出双缆悬索桥的下、上两根主缆的内力的比值，然后统计如表3所示。

表3 主缆内力比值的理论与模型计算结果对比

注：H1为上主缆内力，H2为下主缆内力。

从表2、3可以看出：理论计算和模型计算的误差在容许范围之内，但是误差有一定的规律可寻，当桥塔约束刚度减小时，误差会慢慢增大。而通过分析可以知道，因为上缆的垂跨比很小，对塔顶位移的改变是非常敏感的。桥塔约束刚度k较大时，塔顶的顺桥向位移比较小，利用式(8)计算时可以忽略这种改变，而当约束刚度k逐渐变小时，由桥塔顶位移带来的主缆垂度的改变量会越来越大，所以造成的误差会越来越大。

为了验证这种猜想，又另外增加两种情况：① 单跨悬索桥的两根主缆垂度分别为125和100 m，其对应的垂跨比比值n1/n2为0.8；② 单跨悬索桥的两根主缆垂度分别为125和75 m，其对应的垂跨比比值n1/n2=0.6。得到不同n1/n2的理论计算和模型计算的误差统计结果，见表4。

表4 吊索、主缆统计表

由表4可以看出：随着下上主缆垂跨比的比值不断增大接近1时，也就是两根主缆靠得越近，相对误差越小；表明主缆垂度越大，受力时主缆垂度的改变量相对减小，那么采用式(8)近似计算时，误差就越小，所以在主缆垂度较大时，理论计算的精度会提高。同时可以看出，随着桥塔约束刚度的增加，相对误差会减小，但都在允许的误差范围内。

经过有限元模型和理论计算的相互验证，可以得出理论推导公式是可用的。在文献[8]中，推导出了在桥塔塔顶位移被约束时下吊索和上吊索内力的比值公式，代入该文相应的参数计算出吊索内力比值为6.467。而将该文公式中的参数k设为2×1030N/m时，也就相当于约束塔顶位移时，计算出的比值同样为6.467，佐证了该文推导公式的正确性。

图4为根据理论计算公式(17)探讨桥塔约束刚度对上下吊索内力比值的影响。

图4 桥塔约束刚度对吊索内力比值的影响(理论计算值)

从图4可以发现：桥塔约束刚度存在一个临界值，当桥塔约束刚度取这个临界刚度时，在均布活载作用下，所有的荷载均由下缆承受；约束刚度大于这个临界刚度时，随着刚度的增加，上缆承受的内力比例会慢慢增大，但是会存在一个极限值；当桥塔约束刚度小于这个临界刚度时，上吊索开始出现压力，而且随着刚度的减小，吊索的压力会越来越大；在实际工程中就表现为，桥梁在承受均布荷载时，会使上吊索的预加力减小。这在实际工程中是需要避免的，因为这样上缆不仅起不到有利的作用，反而会成为下缆的累赘，这是不合理的。

4 桥塔约束刚度的计算方法对比分析

4.1 理论公式推导

上文详细介绍了桥塔约束刚度对单跨悬索桥受力的影响，但公式(10)中的k是直接在有限元模型中分别提取水平力H和塔顶顺桥向位移Δx然后利用公式k=H/Δx计算出来的，所以下文将推导桥塔约束刚度的计算公式。

桥塔约束刚度的计算图示如图5所示，计算时不考虑边缆的垂度，作为二力杆处理。

图5 桥塔约束刚度计算简图

在计算桥塔约束刚度时，利用位移法求解结果，首先将结构分成桁架结构和悬臂结构(图6)，假设产生的水平位移协调为Δx，其中桁架结构在水平位移Δx时在塔顶节点产生的水平力为H1,悬臂结构水平位移Δx时在塔顶节点产生的水平力为H2，两个力之和即为总的水平力H。

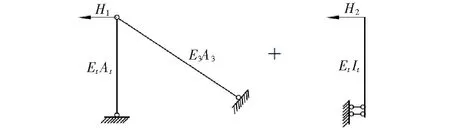
图6 桥塔结构约束刚度计算图

首先确定H1和Δx之间的关系，显然外力H1做的功等于桁架的形变能，其计算式为：

(18)

式中：E3为边缆的弹性模量；A3为边缆的截面面积；α为边缆与水平线的夹角；l为边缆的长度，当悬索桥塔顶到锚碇的高差Δh确定时，l的长度是与倾角α有关的：l=Δh/sinα，该文模型Δh=125 m；Et为桥塔的弹性模量；At为桥塔的截面面积；h为桥塔的高度。

式(18)中没有考虑中跨主缆对桥塔作用的竖直向下的力，这样会引入误差，因此假设中跨主缆的倾角与边缆的倾角相同，所以对桥塔的压力即为2H1tanα，以此考虑中跨主缆对桥塔的压力影响，因为桥塔的轴向变形相对横向位移来说很小，所以忽略中跨主缆产生的竖向外力所做功，式(18)就变为：

(19)

化简式(19)可得桁架结构水平力H1与Δx的比值为定值，设为k1：

(20)

根据结构力学相关知识可知，悬臂梁的顶端水平位移Δx与作用力H2的关系为：

(21)

化简式(21)可得悬臂结构水平力H2与Δx的比值为定值,设为k2：

(22)

由受力条件：

H=H1+H2=k1Δx+k2Δx=(k1+k2)Δx

(23)

将式(20)、(22)代入式(23)并化简，可得桥塔约束刚度：

(24)

4.2 理论与模型结果对比

表5～7为采用式(23)计算得到的桥塔约束刚度与模型结果对比。

表5 主缆垂度为125和100 m的桥塔约束刚度结果对比

表6 主缆垂度为125和75 m的桥塔约束刚度结果对比

表7 主缆垂度为125和50 m的桥塔约束刚度结果对比

由表5～7可以看出：理论计算和模型计算的误差都没有超过0.5%，说明理论计算具有很好的计算精度，为了更好地了解桥塔约束刚度随水平角的变化趋势，绘制桥塔约束刚度与水平倾角的关系图，如图7所示。

图7 桥塔约束刚度与水平倾角的关系图

为了更好地反映出公式的适用性，图7在常用的倾角范围之外额外添加了4个数据点。从图7可以看出：当倾角很小时，理论计算公式和有限元模型的误差很小；而当倾角较大时，理论公式相对于有限元来说有很大的计算误差，这主要是因为在推导理论公式时，考虑了中跨给主塔产生的H1tanα的竖向压力，也就是认为中跨主缆的水平倾角与边缆的水平倾角相同；但是在有限元模型中，只改变边缆的水平倾角，而没有改变中跨的水平倾角，所以当α很大时，就会造成很大的误差。但是常见的悬索桥设计中，边缆的水平倾角一般为25°～45°，所以理论计算公式有很好的适用性。

从图7可以得出这样的结论：当锚碇与主塔顶点的高差一定时，如该文中为125 m，桥塔的约束刚度随着边缆的水平倾角的增大先增大后减小，存在一个最大值。对于这个最大值，可以用一阶导数等于0的原则，求出最大值对应的倾角α。当约束刚度最大时，倾角α满足下式：

ΔhEtAt-3ΔhEtAtsin2α-8hE3A3sin3α=0

(25)

利用式(25)可以求出桥塔约束刚度最大时水平倾角为33.968°，而对应的边缆的水平投影长度为185.55 m，此时理论计算得到的桥塔约束刚度为275 922 kN/m。故式(25)可以应用于悬索桥优化设计中，找出最佳的锚碇设置点，以取得最大的约束刚度。

5 结论

(1)该文在文献[8]的基础上推导出了塔顶无约束时均布荷载作用下单跨双缆悬索桥下吊索内力与上吊索内力比值的计算公式，不仅通过建立有限元模型进行了论证，而且与文献[8]提出的塔顶约束下的计算公式进行横向对比，都证明了公式的正确性，为后续理论的结构分析奠定了基础。

(2)文献[8]中，将塔顶约束处理，代入构件尺寸及材料参数时求出的下上吊索的内力比值为6.467；而该文未将塔顶约束处理，代入同样的参数，求出的下上吊索的内力比值都在15左右，两者差别甚大，所以该文的理论公式推导是有必要的。

(3)通过分析该文推导出的公式，当桥塔的约束刚度超过临界刚度时，随着桥塔约束刚度的增大，单跨双缆悬索桥上缆分配到的荷载比例会慢慢增大。因此在单跨双缆悬索桥设计中为了使上缆分担更多的内力，可以采用增大桥塔约束刚度的方式来达到目的。

(4)在单跨双缆悬索桥设计中，要保证主塔的约束刚度，否则双缆悬索桥的上缆不仅对结构受力起不到有利作用，还会成为整个结构的负担。

(5)该文也提出了桥塔约束刚度的计算公式，并证明了公式的正确性。桥塔的约束刚度与边缆的材料参数以及主塔的材料参数都有关系。当其他材料和构件参数以及锚碇与桥塔顶点的高差确定时，桥塔的约束刚度随着边缆与水平线的倾角增大表现为先增大后减小。该文还确定了最佳倾角的计算公式，可以运用于实际的工程设计中。