赏析浙江物理第6次选考第13题

李 鑫

(浙江桐乡第一中学 浙江 嘉兴 314500)

浙江物理第6次选考引起广泛争议，考试一结束，就有学生指出第13题要用椭圆知识去解决，计算起来颇为棘手，文中称为“椭圆方案”.很多中学教师认为此题和挂衣服问题是一致的，可以利用结论得到答案，文中称为“平衡方案”.本文先对师生提出的方案做了详尽探讨，并提出了一种可以快速求解的“估算方法”.然后就“椭圆方案”和“平衡方案”的内在本质做了比较，指出二者是等价的.探讨完各种解题策略，再提出高考试题中“自相似”现象，辨析了浙江“猴子”问题和天津“挂衣架”问题之间的区别和关联.针对浙江考生把此题当成数学题去做的成因做了分析，就此给出高考复习中如何把握“定式模型”建议.

1 解题方案探讨

【题目】如图1所示，一根绳的两端分别固定在两座猴山的A,B处，A,B两点水平距离为16 m，竖直距离为2 m，A,B间绳长为20 m.质量为10 kg的猴子抓住套在绳子上的滑环从A处滑到B处.以A点所在水平面为参考平面，猴子在滑行过程中重力势能最小值约为(绳处于拉直状态)( )

图1 题目题图

A.-1.2×103J

B.-7.5×102J

C.-6.0×102J

D.-2.0×102J

1.1 椭圆方案

由于猴子到A,B两点距离之和是20，故猴子运动轨迹是椭圆，焦点是A,B两点，问题就划归成一个倾斜椭圆求椭圆上最低点问题.仍沿着长轴和短轴建立坐标系，如图2所示.

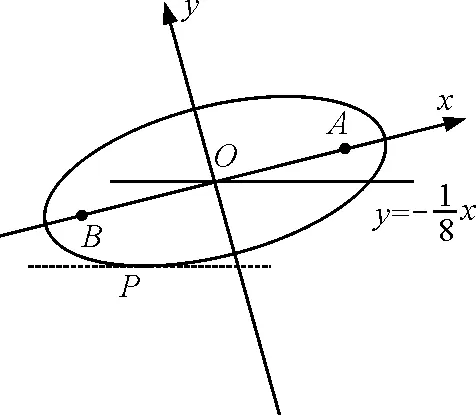
图2 椭圆方案解题示意图

(1)

显然最低点的切线应该沿着水平方向.A，B高度差是2 m水平距离为16 m,所以在此坐标系中该切线斜率

(2)

即过原点平行于水平面的直线方程为

(3)

对椭圆方程进行隐函数求导,两边取微分

即

(4)

此处(x0,y0)即为椭圆最低点坐标，联立可得

(x0,y0)=(-2.067,-5.788)

根据点到直线距离关系有

(5)

知

d=6 m

所以椭圆最低点距离A点的竖直距离是7 m.考虑猴子并非质点，继而得知答案选B.

1.2 平衡方案

从物理角度剖析：这个问题涉及到的思想是最小势能原理，也就是说猴子重力势能最小的时候，它在水平方向是平衡状态.

搞清楚猴子水平方向受力平衡，那么问题就划归成一个常见的定式，如图3所示.

图3 平衡方案解题示意图

猴子在最低点P水平受力平衡，又因为同绳认为滑环两边绳上力相等，即

Tsinα=Tsinβ

(6)

作BP延长线与A处铅垂线交于C，过B做BD垂直于AC，可得

(7)

显然

CD=BCcosα=12

所以P距离A点竖直距离为

和纯数学求解殊途同归.

1.3 估算方案

对于一道选择题，这两种方案处理起来都不简单.此题亦可以用估算，倘若B和A等高，可知猴子轨迹为半长轴和半短轴分别是10和6的一族椭圆，范围在d=2之间，如图4实线到虚线之间.当把椭圆“摆正”，则最低点到焦点高度差为6，即猴子最低点到悬挂点A竖直距离应该介于6和8之间，答案自然是B.

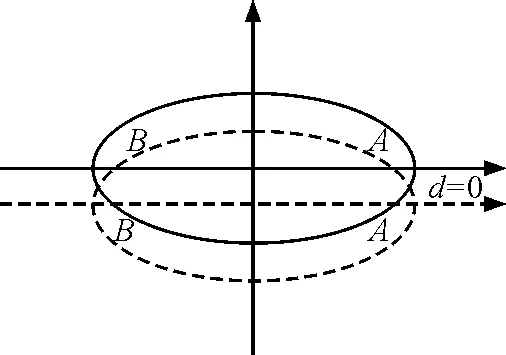
图4 估算方案解题示意图

2 椭圆方案和平衡方案内在关联

从物理角度来说，这是一个最小势能原理结合水平方向受力平衡“一绳两点”定式问题，数学上是基于椭圆轨迹求解最低点问题，那么两者之间有没有联系？如图5所示,过最低点做椭圆切线再做切线的法线，连接最低点和椭圆两个焦点，显然连线与竖直方向夹角相等,这也是椭圆面反射定律体现，即光源从一个焦点发出光线经过椭圆表面反射后必将汇聚在另一个焦点上[1].

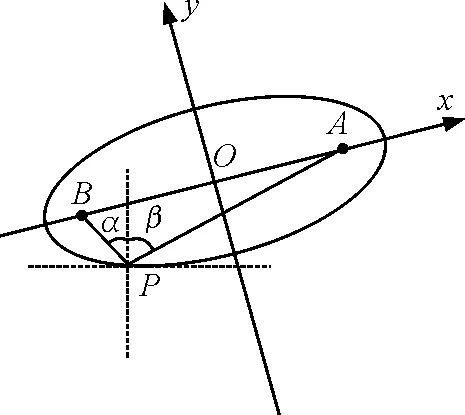
图5 椭圆方案和平衡方案关联示意图

从数学上的椭圆性质再到物理实际问题就完美结合在一起.椭圆最低点，从物理上，是过这点铅垂线平分绳子的夹角，从数学上，是椭圆的一个性质，而椭圆的性质又能反应出椭圆表面光学反射的物理本性.在此素材上深入挖掘，可以让学生体会到数学物理的美丽和内在的自洽统一，继而可以指出一些高中物理应用于解决数学问题的案例，比如最小势能原理的应用[2].

3 比较“猴子”问题和“挂衣架”问题

从“定式”教学来说，很多教师简单地把此题归类到“挂衣架”问题，请看天津这道高考题.

【例题】如图6所示，轻质不可伸长的晾衣绳两端分别固定在竖直杆M,N上的a，b两点，悬挂衣服的衣架钩是光滑的，挂于绳上处于静止状态.如果只人为改变一个条件，当衣架静止时，下列说法正确的是( )

A．绳的右端上移到b′，绳子拉力不变

B．将杆N向右移一些，绳子拉力变大

C．绳的两端高度差越小，绳子拉力越小

D．若换挂质量更大的衣服，则衣架悬挂点右移

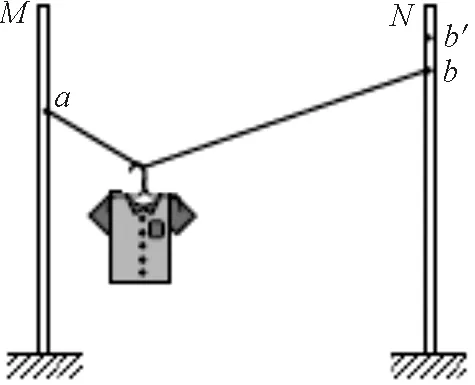
图6 例题题图

衣服受力平衡时，可以得出绳子与竖直方向夹角达到一个定值，这个定值和挂钩在竖直方向位置无关即

(8)

只由挂钩水平方向位移和绳长所决定.在竖直方向上有

2Tcosα=mg

(9)

从而可知A,B正确；C,D错误.

笔者认为这两个问题只是模型上形似，衣服是静止的，而猴子并不是静止的，沿竖直方向是存在加速度的，只是水平方向受力平衡.得到的结论和“挂衣服”相似可以做为定式教学训练用，但是务必要交代清楚物理本质.

再从更广义的角度对比天津“挂衣架”问题和浙江“猴子”问题，两道题出现时间分别是2017年和2018年，时间很靠近，而高考历年试题中不乏这种“自相似”试题，就是一段时间内不同省市对同一个“知识点”或者“物理模型”不约而同考查，比如2010年浙江卷和同年的福建卷都考查同一个问题，即验证胡克定律实验中在弹簧下增挂钩码和减挂钩码效果有什么不同？2007年上海卷和2008年天津卷压轴题都是考查磁悬浮列车模型，而且都源自2006年全国中学生物理竞赛复赛的第5题，关于这样的例子有很多，有兴趣的读者可以自行查阅.

另一个值得关注现象是为什么学生做“猴子”问题时普遍想到是椭圆而不是“挂衣架”呢？高中生经过大量圆锥曲线训练，想到椭圆是很自然的事.想不到“挂衣架”不是因为学生意识到“挂衣架”模型和“猴子”模型上本质的不同，而是因为浙江实行新高考以来，大大压缩物理学习的周期，所以像这种“有些复杂”的定式，被省内大多数物理教师所捐弃，最直接的导向是过去5次新高考从来没有考查过这类定式.事实上“挂衣架”模型是一个成熟的模型，相似问题出现在各类辅导书中.即便训练过“挂衣架”模型的中学生，在实际考试中也很难将“猴子”模型进行迁移.因为浙江“猴子”问题是对天津“挂衣架”问题的超越，不是简单的重复，主要体现在以下两点：

第一，具体问题设置中应用的定式结论不同，天津“挂衣架”问题核心关系式是式(8)，即绳子的夹角由悬挂点水平距离和绳长决定，而浙江“猴子”问题核心关系式是式(7)，是利用相似关系解决一个几何关系.训练过“挂衣架”的学生没有经过延拓，教师只是就题论题，学生可能就拘囿于式(8)而不能稍进一步得到式(7).

第二，最本质的不同是两题建模方式不同，天津“挂衣架”模型指向很清晰，是一个静态受力平衡问题，难点在于数量关系的处理，经过训练后应对换汤不换药的问题，本质没有变，学生容易把握.但是浙江“猴子”问题变成了一个动态过程，问最低点位置是一个几何最值，学生建模时很容易受到数学训练中大量极值问题干扰，喜欢利用函数去解决，没有意识到此题可以通过物理分析得出结论.而且一般处理最低点问题，都是在竖直方向运动，此题猴子做曲线运动，而且不是学生熟知的曲线运动，在不知晓最小势能原理情况下，不易分析得出水平受力平衡切向没有加速度即为猴子轨迹最低点.笔者经过调研，发现通过物理方案解决此题的很多考生并不是很清楚猴子运动特性，而是思维迅速跳到“挂衣架”模型，经过类比解决的，一旦深入分析，他们会感到两者有区别，如果在考场上意识到这个问题，甚至还会怀疑自己.

针对“定式模型”复习，笔者有两点建议：

(1)“定式模型”应该采用发散教学的模式，教师善于引导学生多提问尽可能从更多角度把“定式”理解更透彻，切忌点到为止，就题论题的方式是很低效的，教师讲了很多漂亮的“定式”和结论，但是学生未必能吸收.然后是教师收集改编或自编关于这个“定式”相关习题，集中训练，学生在这个过程中会自觉养成辨识“定式”和应用的能力，能起到良好效果.

(2)笔者认为在进行“定式模型”复习时，最难一点是如何把握讲哪些“定式”，比如过去山东高考题，电磁场问题可以重点讲“轨迹拼接”问题，但是对于北京考生就不必了，北京近些年试题偏爱一些物理本源的理解和推导，所以到底讲解什么“定式”本质上就是把握高考试题动向，教师只有深入本地区试题特点和《考试大纲》才能得出结论，尤其是新高考改革省份，物理教学课时被压缩情况下教师把握动向准不准就显得更加重要了.

4 结论

学生需要较为熟练的数学运算能力才能利用文中解析几何的求解方法，估算方案利用的仍然是椭圆知识，对于解题而言，是个很好的策略.通过对比“平衡方案”和“椭圆方案”，可知从物理和数学角度得出的结论内在是完美统一.然后本文详细探讨学生在考场中实际表现，再分析内在成因.最后比较“猴子”模型和“挂衣架”模型，指出二者在具体应用指向和建模方式上的不同，并给出一些关于高考复习把握“定式模型”的建议.

第13题在浙江省内引起较强烈讨论，笔者以为从课后习题教学来说，这是一个不可多得的好问题.通过数学和物理以及估算多个角度解决问题，再结合不同素材，可以形成一个严密的数学物理知识链，有助于学生科学探究能力的培育.