基于DSP的电动机保护补偿式傅里叶算法研究

付强

1．安徽中电兴发与鑫龙科技股份有限公司技术中心 安徽芜湖 241008

2．安徽省电器设备电磁兼容（EMC）省级实验室 安徽芜湖 241008

3．安徽中电兴发与鑫龙科技股份有限公司 安徽芜湖 241008

半周积分算法，导数算法，两采样值积算法，三采样值的积分算法，由于这些算法都是认为被采样的电流和电压是标准的正弦波，在设备正常运行工作时，一旦发生故障，常常是在基波出现的同时，伴随着有衰减的非周期直流分量以及复杂的高频分量，所以要求微机保护装置预先滤去电压、电流信号中的非周期分量和高频分量，否则计算结果将远远偏离实际值，使计算误差变大。虽然全波傅氏算法具有稳定性好的优点，在滤波过程中能够滤除所有整数次的谐波分量，而且运算工作量比较小[1-2]。

1 补偿式傅氏算法的计算推导步骤

通过以上新算法的整个计算推导过程，综合分析可知，导致算法计算工作量较大的是半个周期后第3个采样间隔中的数值，但是此种算法的计算时间仅仅约，完全可以满足微机保护装置实时控制的要求。补偿式半波傅氏算法不但继承了原由半波傅里叶算法的有点，而且又增加了对衰减非周期得直流分量的过滤功能。此种新算法所采用的数据窗仅仅为半个周期采样值加上两个采样点，式算法的计算更加简便，计算速度快，计算精度高，并且很好地滤除了衰减的非周期直流分量，而且此种功能又可以完全不受衰减的非周期的直流分量时间常数大小所限制[3]。

2 补偿式全波及半波傅氏算法仿真

为了验证以上算法的正确性、精度以及合适的应用范围，对以上算法进行仿真并进行了比较：

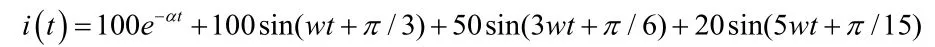
相应改变α，傅氏算法，补偿式新傅氏算法算出的基波分量、角度的值及误差如下表所示。

表1 各种算法的滤波效果比较

3 结语

综上所述，补偿式半波傅氏算法不但继承了原有半波傅里叶算法的优点，而且又增加了对衰减非周期得直流分量的过滤功能。此种新算法所采用的数据窗仅仅为半个周期采样值加上两个采样点，算法的计算更加简便，计算速度快，计算精度高，并且很好地滤除了衰减的非周期直流分量，而且此种功能又可以完全不受衰减的非周期的直流分量时间常数大小所限制。