一次关于“列方程教学”的访谈与思考*

●

(海曙区古林镇中学，浙江 宁波 315176)

1 访谈背景

2 访谈实录

问：根据实际问题的条件列方程的教学要经历哪几个步骤？

答：审题→分析→设元→列方程．

问：审题主要审什么？

答：审问题涉及的量、已知的量、未知的量、所求的量．

问：主要分析什么？

答：分析问题中含有的数量关系．

问：设元的含义是什么？

答：设元就是选择一个适当的未知数用字母表示．

问：列方程呢？

答：列方程就是根据等量关系列出方程．

问：针对下列问题的方程你是怎样教学的？

例1某文艺团体为“希望工程”募捐义演，全价票为每张18元，学生享受半价．某场演出共售出966张票，收入15 480元，问这场演出共售出学生票多少张？

答：第一，引导学生阅读题目并找出问题涉及的数量：票数、票价、总价等．

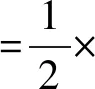
第三，设哪个未知数为x(本题应设学生票张数为x张).

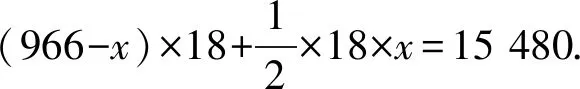
3 访谈后的思考

通过课堂观察发现，上述教师持有的列方程的教学过程观具有普遍性，它主要来自于浙教版教材提供的观点——运用方程解决实际问题的一般过程：

1)审题：分析题意，找出题中的数量及其关系;

2)设元：选择一个适当的未知数用字母表示(例如x);

3)列方程：根据相等关系列出方程;

4)解方程：求出未知数的值；

5)检验：检查求得的值是否正确和符合实际情况，并写出答案[1]．

事实上，用方程解决实际问题的教学性质是问题解决教学，它要经历问题解决的4个基本步骤：理解问题→制定计划→执行计划→回顾[2]．这里理解问题主要是：审问题含有的数量、已知量、未知量、所求量，审问题含有的等量关系，特别是含有未知量的等量关系.制定计划主要是：在分析各种可行的列方程方案的基础上，选择一个比较合适的方案．而目前根据实际问题的条件列方程的教学隐去了列方程之前分析与决策的过程，并且选哪个未知数用字母表示带有盲目性，这样所列的方程不一定合适，如果审题时未知量有遗漏，也得不到相应的方程，这样的教学失去了发展学生能力和个性的机会，这种尝试性列方程的方法不利于学生积淀经验，这可能是导致学生列方程困难的根本原因．

4 列方程教学改进建议

笔者认为，列方程的教学过程是：审题(审已知量、未知量、所求量；审含有未知量的等量关系，即用列式、列表、画图等方法，找出问题中含有未知量的等量关系)→分析(列方程有哪些方案，哪个方案比较合适，即选用哪个含有未知量的等量关系来列方程和哪个未知数用字母表示比较合适——使所列方程求解方便)→设未知数、列方程(根据确定的方案用字母表示未知数并列出方程)．这里列方程之前有分析与决策的过程，并且选哪个未知数用字母表示有指向性，它依赖于选用的含有未知量的等量关系，即使审题时遗漏了某个未知量，在选用含有未知量的等量关系来列方程时也能发现，使得学生列方程有规律可循，从而为学生提供了发展能力和个性的机会，特别是这种带有规律性的列方程方法有助于学生积淀经验．

下面以浙教版《数学》七年级上册第5.4节“一元一次方程的应用(第一课时)”中的例1与例2为载体，来展示用方程解决实际问题的教学过程．

例2同例1.

师：问题中含有哪些数量？哪些是已知的？哪些是未知的？哪些是所求的？

生1：问题中含有的数量有总票数、全价票张数、学生票张数、全价票的票价、学生票的票价、总收入、全价票的收入、学生票的收入，其中已知量是总票数、全价票的票价、学生票的票价、总收入，未知量是全价票张数、学生票张数、全价票的收入、学生票的收入，所求量是学生票张数．

师：很好！用分类方法来提取问题中的数量信息．问题中含有哪些等量关系？

生2：全价票张数×全价票的票价=全价票的收入；学生票张数×学生票的票价=学生票的收入；全价票张数+学生票张数=966；全价票的收入+学生票的收入=15 480．

师：不错!其实，在这4个等量关系中可以提炼出2个含有未知量的等量关系，即全价票张数+学生票张数=966；全价票张数×18+学生票张数×9=15 480．

师：那么选用哪个含有未知量的等量关系来列方程，选用哪个未知数用字母来表示比较合适?有哪些方案？

生3：用“全价票张数×18+学生票张数×9=15 480”来列方程，学生票张数用字母来表示(或全价票张数用字母来表示)；也可用“全价票张数+学生票张数=966”来列方程，学生票张数用字母来表示(或全价票张数用字母来表示)．

生4：选用“全价票张数×18+学生票张数×9=15 480”来列方程和学生票张数用字母表示比较合适．

师：根据你确定的方案，可列出怎样的方程？

生4：设学生票张数为x，则

(966-x)×18+9x=15 480．

师：好的．请大家解这个方程，并通过检验回答实际问题的答案．

师(待学生完成任务)：谁来汇报学习结果？

生5：x=212．经检验它是方程的解且符合实际意义,即这场演出共售出学生票212张．

师：这样我们用一元一次方程解决了这个问题，解题过程的规范表达请参考课本．若选其他方案，则可列出怎样的方程？

生6：用“全价票张数×18+学生票张数×9=15 480”来列方程.设全价票张数为x，则可列出方程18x+(966-x)×9=15 480．

生7：用“全价票张数+学生票张数=966”来列方程，设全价票张数为x张，则可列出方程

生8：用“全价票张数+学生票张数=966”来列方程.设学生票张数为x，则可列出方程

师：由此可知，经历分析基础上选择性决策的过程，能使所列的方程更加合适．

……

例3A，B两地相距60 km，甲、乙两人同时从A，B两地骑自行车出发，相向而行．甲每小时比乙多行2 km，经过两个小时相遇．问甲、乙两人的速度分别是多少？

师：请大家依次思考并回答下列问题(允许小组合作).

1)问题中含有哪些未知量？有哪些含有未知量的等量关系？

2)选用哪个含有未知量的等量关系来列方程,选用哪个未知数用字母来表示比较合适?有哪些方案？

3)根据你确定的方案，可列出怎样的方程？

师(待学生思考完毕)：谁来回答问题1)？

生9：问题中含有的未知量为甲行驶的速度、路程以及乙行驶的速度、路程．问题中含有未知量的等量关系为“甲行驶路程+乙行驶路程=60”和“甲的速度=乙的速度+2”．

师：好的．谁来回答问题2)？

生10：用“甲行驶路程+乙行驶路程=60”来列方程，乙的速度用字母表示(或甲的速度用字母表示)；也可用“甲的速度=乙的速度+2”来列方程，甲行驶路程用字母表示(或乙行驶路程用字母表示)．用“甲行驶路程+乙行驶路程=60”来列方程和乙的速度用字母表示比较合适．

师：有道理．谁来回答问题3)？

生11：设乙的速度为x，则可列出方程2(x+2)+2x=60．

师：好的．请大家完整地把解题过程写出来．

……

师(待学生完成任务)：若选其他方案，则可列出怎样的方程？

生12：若选用“甲行驶的路程+乙行驶的路程=60”来列方程，设甲的速度为y，则可列出方程

2y+2(y-2)=60．

生13：若选用“甲的速度=乙的速度+2”来列方程，设甲行驶的路程为S，则可列出方程

若选用“甲的速度=乙的速度+2”来列方程，设乙行驶的路程为S，则可列出方程

师：由此可知，每一个含有未知量的等量关系都可以用来列方程，设未知数也有直接设元法和间接设元法两种，但选哪个未知数用字母表示依赖于所选用的含有未知量的等量关系．这进一步说明要使所列的方程更加合适，就要经历分析基础上的选择性决策的过程．

初步的理论求证与实践验证表明，改进后列方程的教学过程遵循了问题解决教学的基本规范，体现了过程教育和以学为中心的思想，它不但有助于学生积淀列方程的经验，而且对促进学生发展智力、能力和个性也有积极的影响．