非饱和粗粒土基质吸力与含水率及级配关系试验研究

何忠明，刘雅欣，曾新发，刘登生，职孟林



非饱和粗粒土基质吸力与含水率及级配关系试验研究

何忠明1, 2，刘雅欣2，曾新发3，刘登生4，职孟林5

(1. 长沙理工大学 公路养护技术国家工程实验室，湖南 长沙，410014；2. 长沙理工大学 交通运输工程学院，湖南 长沙，410014；3. 湖南城市学院 土木工程学院，湖南 益阳，413000；4. 中交(天津)生态环保设计研究院有限公司，天津，300450；5．河南省交通规划勘察设计院，河南 郑州，450000)

为了研究非饱和粗粒土基质吸力与含水率及级配之间的关系，通过控制曲率系数和不均匀系数配制5种不同级配的粗粒土土样，采用自行设计的模型装置进行降雨入渗试验，并根据试验结果绘制基质吸力与含水率关系拟合曲线，得到满足试验条件的函数关系式，从而得到土−水特征曲线方程。研究结果表明：不均匀系数越大，土样初始含水率越小，达到饱和状态时含水率越小，且土样达到饱和所需的时间越长；随着脱水过程的进行，土样不均匀系数越大，其含水率的下降速度越慢，残余含水率也越大；初始基质吸力随着土样不均匀系数增大而不断提高，同时，土样的残余基质吸力随着不均匀系数增大而增大；利用Van Genuchten模型对实测土−水特征曲线进行拟合可获得拟合参数，从而得到可应用于数值分析的土−水特征曲线方程。

粗粒土；级配；基质吸力；含水率；土水特征曲线

土−水特征曲线主要研究土体基质吸力与含水率之间的关系，是非饱和土力学中主要研究内容[1−2]。随着粗粒土在工程中的广泛应用，研究者对粗粒土土−水特征曲线的研究也逐步深入。对非饱和土而言，土体的级配对其基质吸力与含水率的分布特征有重要影响[3−4]。土体内部水分子的定向移动总是从能量高的地方向能量低的地方流动，当土体孔隙内的水所含能量比孔隙之外的水能量高时，孔隙内的水会流向孔隙外部，反之，土体就会将孔隙外部的水吸入其内部[5−6]。土−水特征曲线反映非饱和土中含水率与基质吸力之间的关系[7−8]，它对研究非饱和土的相关性质非常重要，因为土体的诸多参数如抗剪强度、渗透性能等均能在土水特征曲线中得到体现[9−14]。VANAPALLI 等[15]研究了非饱和土的级配与土−水特征曲线之间的关系。李志清等[16]通过室内外降雨试验，推算了土体在非饱和情况下的抗剪强度、渗透性、土体矿物组成以及应力等多种因素对土−水特征曲线的影响。毛尚之[17]基于特定膨胀土在不同应力条件下的降雨试验，得到应力对土−水特征曲线的影响规律。SILLERS 等[18]通过对不同土体的土−水特征曲线模型进行统计分析，得出现有土−水特征曲线模型的均值、中值和均方差均存在较大偏差。目前，人们针对级配变化对基质吸力与含水率关系的影响研究较少，为此，本文作者拟通过控制曲率系数c和不均匀系数u来配制5种不同级配的粗粒土土样；然后，采用自行研制的模型装置进行室内降雨试验，对试验结果进行分析后得到粗粒土基质吸力、含水率随级配的变化规律，以便为工程应用提供参考。

1 土−水特征曲线基本理论

1.1 典型土−水特征曲线

典型土−水特征曲线一般分为3个阶段：边界效应段、过渡段和非饱和残余段，见图1。在边界效应段内，基质吸力变化对含水率无显著影响；当基质吸力增大到某个临界值时，土体的基质吸力大于孔隙的抵抗力，土体孔隙中的水将被排出，土体含水率会相应降低，这个临界值称为进气值[11]。随后，土−水特征曲线进入过渡段，此时，土体基质吸力逐渐增大，造成土中较大的孔隙开始向外排水，较小的孔隙也开始排水。随着基质吸力继续增大，曲线进入非饱和残余段，在此阶段，无论土体的基质吸力如何变化，其含水率并不会产生明显变化，而是趋向于某一个稳定值，土体中除了细小的孔隙外，其他孔隙均不含自由水，此时，土体的含水率称为残余含水率[12]。

图1 典型土−水特征曲线

1.2 土−水特征曲线数学模型

理论上，直接建立土体基质吸力与含水率的关系非常困难，目前，国内外学者通过试验结果并结合相应的数学模型来获得土−水特征曲线，其中较经典的数学模型有 Mualem模型、Fredlund和Xing模型、Van Genuchten模型、Gardner模型和Brooks-corey模型等，其中最常用的Van Genuchten模型公式为[19−21]

式中：为土壤含水率；r为残余含水率；θ为饱和含水；，和为经验系数；为压力水头。

2 不同级配粗粒土室内降雨模型试验

2.1 土样级配的确定

固定曲率系数c不变，改变不均匀系数u，制备试验所需的5种级配土样，具体级配见表1，试验土样粒径见表2，试验土样的不均匀系数和曲率系数见表3。根据不同不均匀系数u，将土样依次编号为土样1、土样2、土样3、土样4和土样5，级配曲线按照横坐标为对数坐标，如图2所示。

表1 不同试验土样颗粒级配

表2 不同试验土样粒径

注：10，30和60分别为分布曲线上小于该粒径的试样质量占总质量的10%，30%和60%的粒径。

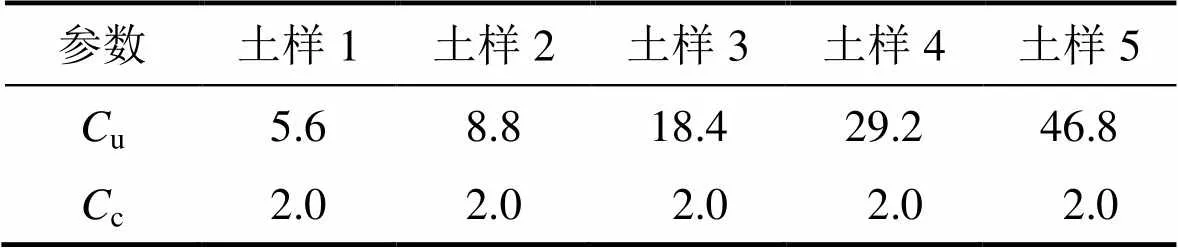
表3 试验土样的不均匀系数Cu和曲率系数Cc

1—土样1；2—土样2；3—土样3；4—土样4；5—土样5。

2.2 试验设备的制作及试验用土的制备

本文使用的降雨入渗试验设备主要由有机玻璃筒、土工筛、电子秤、含水率测试仪、张力计等组成。

1) 本试验采用定制的有机玻璃筒如图3所示，筒高为800 mm，直径为400 mm，壁厚为5 mm。筒壁钻有4个直径为25 mm的圆孔。为了方便控制试验用土的压实效果，在有机玻璃筒的顶部设有压实控制线，该线距离有机玻璃筒的顶部50 mm。

图3 有机玻璃筒

2) 本试验采用的含水率测试仪(型号B−10A，电源电压为3.3 V，输出电流为4~20 mA)测量范围为0~100%，测量精度为1%；张力计(北京奥特斯达科技有限公司)测量范围为0~80 kPa，测量精度为1 kPa。

试验时，首先将从高速公路路堤施工现场取回的粗粒土晾晒，随后将土样分别采用圆孔直径为0.10，0.25，1.00，2.00，5.00，10.00和20.00 mm的土工筛进行筛分，将筛分后的土体按照试验所需的级配曲线进行称量配比并搅拌均匀，制备符合级配要求的粗粒土。根据现场的击实试验得到土体的最大干密度为1.5 g/cm3。由于玻璃筒能承受土样的最大体积为 94 200 cm3，因此，计算出试验所需土体的总质量为141.3 kg。

2.3 降雨入渗试验过程

1) 首先，将蒸馏水沿着张力计内壁缓慢注入张力计中，直至水完全充满张力计，然后塞上橡皮塞，拧紧玻璃帽；通过纸巾擦拭张力计的陶瓷头将张力计表盘读数归零。

2) 将试验所需的粗粒土进行分层压实，当土体到达钻孔位置时，将调试好的张力计通过钻孔插入，将含水率传感器探头埋设在与张力计相同的高度，并利用玻璃胶将张力计与钻孔处进行密封，以防漏水。安装完成后，静至24 h，记录3个张力计和3个含水率测试仪的读数，分别求其平均值，将平均值分别作为土样的初始基质吸力和初始含水率。

3) 本次试验设置的降雨强度为1.16×10−6m/s，该降雨强度为工程所在地近10年来单日最大降雨强度，对降雨装置进行调节，使降雨均匀覆盖整个土样表面。

4) 开始降雨之后，每隔1 h测1次数据，直至土样达到饱和状态，随后，打开玻璃筒底部的排水阀排水，同样每隔1 h读1次数据，直至数据不再发生变化为止。为了尽量减少误差，每次测量读3次，并将3次试验结果求平均值，作为测量的基质吸力与含水率的最终值。

2.4 试验结果

2.4.1 含水率变化规律

图4所示为不同试验土样含水率随降雨时间的变化曲线。

1—土样1；2—土样2；3—土样3；4—土样4；5—土样5。

从图4可以看出：土样1至土样5的初始含水率分别为7.6%，7.3%，6.9%，6.5%和6.3%，呈现下降趋势；饱和含水率分别为37.6%，36.7%，35.3%，34.6%和33.4%，同样呈现下降趋势；残余含水率分别为17.2%，18.7%，19.6%，20.2%和21.6%，呈现上升趋势。经过分析可知：不均匀系数越大，土样初始含水率越小，降雨开始后，土样的体积含水率不断升高，在达到饱和之前，各个土样含水率变化趋势几乎一致；同时，随着不均匀系数增大，土样达到饱和所需时间越长，且土样饱和含水率越小。降雨停止时，打开模型底部的排水阀，土样进入脱水过程，在这个过程中，土样不均匀系数越大，其含水率下降速度越慢，并最终保持不变，此时，含水率称为土体残余含水率，随着土样不均匀系数增大而增大。

产生上述现象的原因是：土样不均匀系数越大，土样颗粒的粒径分布越均匀，土体级配越好而土颗粒之间的孔隙越小，导致土体饱和渗透系数越小，进而造成降雨条件下雨水下渗速度缓慢，表现出在相同降雨强度下，土样不均匀系数越大，土体达到饱和状态所需要的时间越长。因为土样的不均匀系数大，造成土颗粒之间的孔隙小，雨水可填充的孔隙就少，因此，在降雨条件下，土样的饱和含水率随着不均匀系数增大而不断减小，造成土样在脱水过程中含水率降低速度慢，土样的孔隙小，增强了土样的持水能力。

2.4.2 基质吸力变化规律

图5所示为不同试验土样基质吸力随降雨时间的变化规律。

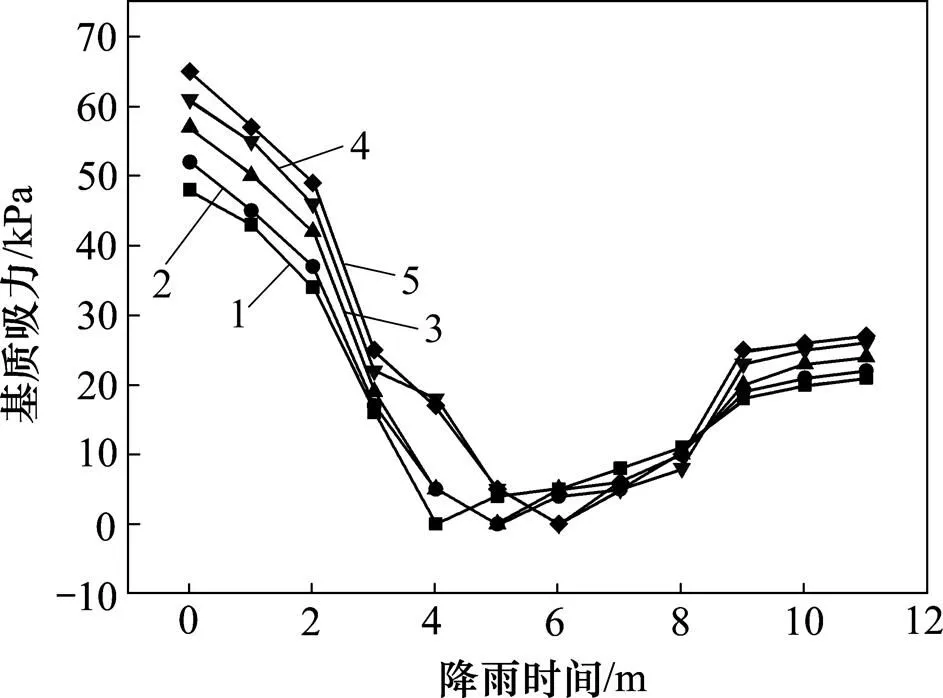
1—土样1；2—土样2；3—土样3；4—土样4；5—土样5。

分析图5可以得出：降雨开始前土样1至土样5初始基质吸力分别为48，52，57，61和65 kPa，初始基质吸力随着土样不均匀系数的增大而不断升高；降雨开始后，土样的基质吸力随着降雨时间持续而不断降低，且最终基质吸力为0 kPa，此时，土样达到饱和状态；降雨停止并打开模型底部的排水阀时，土样进入脱水过程，在这个过程中，土样的基质吸力随着脱水时间的持续而不断升高，经过一段时间后，土样的基质吸力保持稳定，此时，土样1至土样5的残余基质吸力分别为22，24，26，28和29 kPa，证明土样的残余基质吸力随着不均匀系数的增大而增大。

土样1至土样5的初始基质吸力和最终残余基质吸力均随着土样不均匀系数增大而增大，这是因为土样不均匀系数越大，土体的级配越好，而土颗粒之间的孔隙越小，造成土样对水的吸附能力越强。土样体积含水率的变化规律与基质吸力的变化规律具有一定的相对性，这是因为土样基质吸力随着土体体积含水率的增大而减小，如当土样的体积含水率达到最大时，其基质吸力基本为0 kPa；当土样的体积含水率降到最低值时，则基质吸力达到最大值。

3 土−水特征曲线绘制及拟合

3.1 土−水特征曲线绘制

土水特征曲线是研究非饱和土性质中非常重要的曲线，其含义为土的含水率与吸力之间的关系曲线，它反映了土的持水能力和特性。本文选用体积含水率和基质吸力等参数对试验土样进行研究，通过模型试验绘制基质吸力与含水率关系拟合曲线。不同试验土样的基质吸力与含水率关系曲线的拟合参数见表4，不同试验土样基质吸力与含水率的关系见图6。

从表4可知：土样的不均匀系数对土体的基质吸力及含水率均有重要影响，对于含水率而言，不均匀系数越大，土体含水率下降速度越小。从图6可知：土样1至土样5这的初始含水率分别为37.6%，36.7%，35.3%，34.6%和33.4%，它们随着土样不均匀系数增大而减少；土样1至土样5的残余含水率分别为17.2%，18.7%，19.6%，20.2%和21.6%，它们随着土样不均匀系数的增大而增大。总体上，土样不均匀系数越大，曲线初始含水率越小，且含水率随着基质吸力的增大而不断减小；当基质吸力基本保持不变时，不均匀系数大的土样，其残余含水率反而比不均匀系数小的土样大。造成上述现象的原因是：土样不均匀系数增大导致孔隙比减小和土体自身渗透系数减小，且空气进出更加困难，进而导致土样的排水能力较弱；同时，孔隙比小的土样在脱水过程中，由于其孔隙间的持水能力较强，造成不均匀系数大的土样残余含水率比不均匀系数小的土样大。

3.2 土−水特征曲线拟合

根据试验结果对土−水特征曲线的形态和变化规律进行描述，利用数学模型得到土−水特征曲线的经验方程[16]。本文以基质吸力为自变量，体积含水率为因变量，选用Van Genuchten模型对土−水特征曲线进行拟合分析。由于土样1和土样5的级配差距最大，为了便于对比，选取土样1和土样5进行拟合，拟合结果分别如图7和图8所示。

从表5可以看出：土样1和土样5的土−水特征曲线拟合相关系数R均在0.99以上，说明拟合效果良好。模型经验系数和先通过拟合得到，代入Van Genuchten模型公式即可进一步得到土−水特征曲线经验方程，用于后续粗粒土路堤稳定性计算或者降雨入渗量计算。应用本文得到的土水特征曲线，可对粗粒土数值分析时所需相关参数进行合理赋值，使数值分析结果更加符合工程实际。

表4 不同试验土样基质吸力与含水率关系曲线拟合参数

1—土样1；2—土样2；3—土样3；4—土样4；5—土样5。

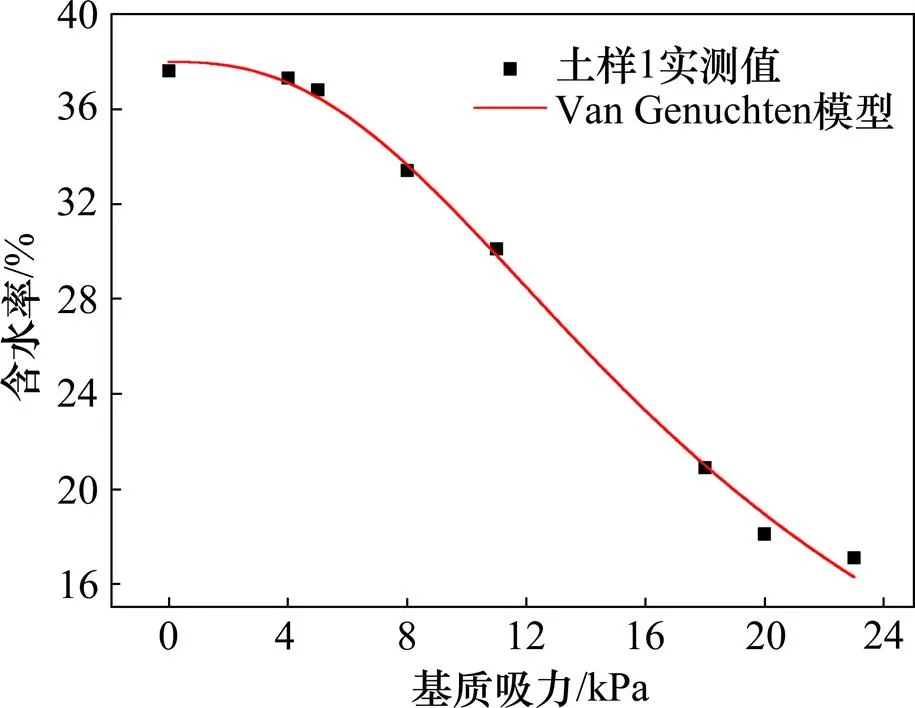
图7 土样1的基质吸力与含水率关系拟合曲线

图8 土样5的基质吸力与含水率关系拟合曲线

表5 土样1和土样5基质吸力与含水率关系曲线的拟合参数

Table 5 Moisture content and matrix suction curve fitting parameter of soil sample 1 and 5

4 结论

1) 不均匀系数越大，土样初始含水率越小；随着不均匀系数增大，土样达到饱和所需的时间越长，且土样饱和含水率越小。

2) 土样在脱水过程中，不均匀系数越大，其含水率下降速度越小，且最终残余含水率随着土样不均匀系数的增大而增大。

3) 初始基质吸力随着土样不均匀系数增大而不断升高；土样在脱水过程中，其基质吸力随着脱水时间的持续而不断升高，且最终土样的残余基质吸力随着不均匀系数增大而增大。

4) 利用Van Genuchten模型对实测土−水特征曲线进行拟合，获得拟合参数，从而可得到应用于数值分析过程中的土−水特征曲线经验方程。在后续粗粒土路堤稳定性计算或者降雨入渗计算过程中，应用本文方法得到的土水特征曲线对数值分析所需相关参数合理地赋值，可使数值分析结果更加符合工程实际。

[1] 黄文熙. 土的工程性质[M]. 北京: 水利电力出版社, 1983: 68−91. HUANG Wenxi. Engineering properties of soil[M]. Beijing: China Water Power Press, 1983: 68−91.

[2] 马吉倩, 付宏渊, 王桂尧, 等. 降雨条件下成层土质边坡的渗流特征[J]. 中南大学学报(自然科学版), 2018, 49(2): 464−471. MA Jiqian, FU Hongyuan, WANG Guiyao, et al. Seepage characteristics of layered soil slope under rainfall conditions[J]. Journal of Central South University(Science and Technology), 2018, 49(2): 464−471.

[3] 王协群, 邹维列, 骆以道, 等. 压实度与级配对路基重塑黏土土−水特征曲线的影响[J]. 岩土力学, 2011, 32(S1): 181−186.WANG Xiequn, ZOU Weilie, LUO Yidao, et al. Effects of compaction degree and gradation on soil-water characteristic curve of roadbed remolded clay[J]. Rock and Soil Mechanics, 2011, 32(S1): 181−186.

[4] 郑俊杰, 郭震山, 崔岚, 等. 考虑非饱和渗流与增湿膨胀下的膨胀土隧道稳定性分析[J]. 岩土力学, 2017, 38(11): 3271−3277. ZHENG Junjie, GUO Zhenshan, CUI Lan, et al. Stability analysis of expansive soil tunnel considering unsaturated seepage and moistening swelling deformation[J]. Rock and Soil Mechanics, 2017, 38(11): 3271−3277.

[5] 张鹏程, 汤连生, 姜力群, 等. 基质吸力与含水量及干密度定量关系研究[J], 岩石力学与工程学报, 2013, 23(5): 2792−2797. ZHANG Pengcheng, TANG liansheng, JIANG Liqun, et al. Quantitative relationship between soil suction and water content and dry density[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 23(5): 2792−2797.

[6] 文海家, 张岩岩, 付红梅, 等. 降雨型滑坡失稳机理及稳定性评价方法研究进展[J]. 中国公路学报, 2018, 31(2): 15−29, 96. WEN Haijia, ZHANG Yanyan, FU Hongmei, et al. Research status of instability mechanism of rainfall-induced landslide and stability evaluation methods[J]. China Journal of Highway Transporation, 2018, 31(2): 15−29, 96.

[7] 简文星, 许强, 童龙云. 三峡库区黄土滑坡降雨入渗模型研究[J]. 岩土力学, 2013, 34(12): 3527−3533. JIAN Wenxing, XU Qiang, TONG Longyun. Rainfall infiltration model of Huangtupo landslide in Three Gorges Reservoir area[J]. Rock and Soil Mechanics, 2013, 34(12): 3527−3533.

[8] 张建, 李江腾, 林杭, 等. 降雨触发浅层坡体失稳的迟滞现象及其与土质参数的关联性[J]. 中南大学学报(自然科学版), 2018, 49(1): 150−157. ZHANG Jian, LI Jiangteng, LIN Hang, et al. Delay phenomenon of shallow slope failure triggered by rainfall and its correlation with soil parameters[J]. Journal of Central South University(Science and Technology), 2018, 49(1): 150−157.

[9] 申存科, 迟世春, 贾宇峰. 考虑颗粒破碎影响的粗粒土本构关系[J]. 岩土力学, 2010, 31(7): 2111−2115. SHEN Cunke, CHI Shichun, JIA Yufeng. Constitutive relations of coarse grained soil with particle crushing[J]. Rock and Soil Mechanics, 2010, 31(7): 2111−2115.

[10] 刘磊, 殷坤龙, 徐勇, 等. 考虑降雨及库水位变动的区域滑坡灾害稳定性评价研究[J]. 岩石力学与工程学报, 2018, 37(2): 403−414. LIU Lei, YIN Kunlong, XU Yong, et al. Evaluation of regional landslide stability considering rainfall and variation of water level of reservoir[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(2): 403−414.

[11] 张磊, 张璐璐, 程演, 等. 考虑潜蚀影响的降雨入渗边坡稳定性分析[J]. 岩土工程学报, 2014, 36(9): 1680−1687. ZHANG Lei, ZHANG Lulu, CHENG Yan, et al. Study on stability of rainfall infiltration slope considering the influence of potential erosion[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(9): 1680−1687.

[12] 卢应发, 陈高峰, 罗先启, 等. 土−水特征曲线及其相关性研究[J]. 岩土力学, 2014, 29(9): 2481−2486. LU Yingfa, CHEN Gaofeng, LUO Xianqi, et al. Study on soil-water characteristic curve and its correlation[J]. Rock and Soil Mechanics, 2014, 29 (9): 2481−2486.

[13] 左威, 郑明新, 孙斌. 基于PF土−水特征曲线的非饱和土渗透特性预测[J]. 中外公路, 2011, 38(2): 26−28. ZUO Wei, ZHENG Mingxin, SUN Bin. Performance prediction of unsaturated soil based on PF soil-water characteristic curve[J]. Journal of China & Foreign Highway, 2011, 38(2): 26−28.

[14] FREDLUND D G, XING A, HUANG S. Predicting the permeability function for unsaturated soils using the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 533−546.

[15] VANAPALLI S K, FREDLUND D G, PUFAHL D E. The relationship between the soil-water characteristic curve and the unsaturated shear strength of a compacted glacial till[J]. Geotechnical Testing Journal, 1996, 19(3): 259−268.

[16] 李志清, 胡瑞林, 王立朝, 等. 非饱和膨胀土SWCC研究[J]. 岩土力学, 2016, 27(5): 730−737. LI Zhiqing, HU Ruilin, WANG Lichao, et al. SWCC study of unsaturated expansive soils[J]. Rock and Soil Mechanics, 2016, 27(5): 730−737.

[17] 毛尚之. 非饱和膨胀土的土−水特征曲线研究[J]. 工程地质学报, 2012, 10(2): 129−133. MAO Shangzhi. Study on soil-water characteristic curves of unsaturated expansive soils[J]. Journal of Engineering Geology, 2012, 10(2): 129−133.

[18] SILLERS W S, FREDLUND D G, ZAKERZADEH N. Mathematical attributes of some soil-water characteristic curve models[J]. Geotechnical and Geological Engineering, 2011, 19(3/4): 243−283.

[19] GENUCHTEN V. A closed-from equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 18(14): 892−898.

[20] NIE Wen, HUANG Runqiu, CHEN Yulong, et al. Optimization of groundwater 1D multi-tank model based on physical experiments[J]. Electronic Journal of Geotechnical Engineering, 2014, 19(6): 8827−8841.

[21] 张昭, 刘奉银, 张国平. 土在全含水率范围内持水及非饱和渗透特性的模型描述[J]. 岩土工程学报, 2014, 36(11): 2069−2077. ZHANG Zhao, LIU Fengyin, ZHANG Guoping. Models for water retention and unsaturated permeability in full range ofwater content[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(11): 2069−2077.

Experimental study on relationship among matric suction and moisture content and gradation of unsaturated coarse grained soil

HE Zhongming1, 2, LIU Yaxin2, ZENG Xinfa3, LIU Dengsheng4, ZHI Menglin5

(1. State Engineering Laboratory of Highway Maintenance Technology, Changsha University of Science & Technology, Changsha 410014, China;2. School of Traffic and Transportation Engineering, Changsha University of Science & Technology, Changsha 410014, China;3. College of Civil Engineering, Hunan City University, Yiyang 413000, China;4. China Communications(Tianjin) Environmental Protection Design and Research Institute Co. Ltd., Tianjin 300450, China;5. Communications Planning and Design Institute Co. Ltd of Henan Province, Zhengzhou 450000, China)

In order to study the relationship among matric suction and moisture content and gradation of unsaturated coarse grained soil, five kinds of coarse-grained soil samples with different gradations were prepared by controlling curvature coefficient and non-uniform coefficient. The rainfall infiltration test was conducted using a self-designed model device. The fit curves of moisture content with matrix suction were plotted based on the experimental results, and the functional relationship under the experimental conditions was obtained. The results show that the bigger the non-uniform coefficient, the smaller the initial moisture content of the soil sample, and the smaller the water content, the longer it takes for the soil sample to reach saturation. With the progress of the dehydration process, the larger the non-uniform coefficient of the soil sample, the slower the rate of decline of its moisture content, and the greater the final residual moisture content. The initial matrix suction increases with the increase of the non-uniform coefficient of the soil sample. The residual matrix suction of the soil sample increases with the increase of the non-uniform coefficient. Using the Van Genuchten model to fit the measured soil-water characteristic curve, the fitting parameters can be obtained, so that the empirical equation of the soil-water characteristic curve applied in the numerical analysis process can be obtained.

coarse grained soil; gradation; matric suction; water content; soil water characteristic curve

U416

A

1672−7207(2019)03−0712−07

10.11817/j.issn.1672-7207.2019.03.026

2018−06−08；

2018−08−18

国家自然科学基金资助项目(51678073，51508042，51838001) (Projects(51678073, 51508042, 51838001) supported by the National Natural Science Foundation of China)

曾新发，博士，副教授，从事岩土工程、结构振动控制研究；E-mail：zengxinfa126@126.com

(编辑 陈灿华)