基于附面层理论的路基热边界模型

罗晓晓，俞祁浩，马勤国，张建明



基于附面层理论的路基热边界模型

罗晓晓1, 2，俞祁浩1，马勤国3，张建明1

(1. 中国科学院西北生态环境资源研究院 冻土工程国家重点实验室，甘肃 兰州，730000；2. 中国科学院大学 工程科学学院，北京，100049；3. 华南理工大学 亚热带建筑科学国家重点实验室，广东 广州，510641)

基于“附面层原理”，建立考虑气象条件和路面结构热物理因素影响下的路面结构热交换计算模型。选用合适的判据给出热边界厚度的确定方法，然后，通过数值模拟和灰关联分析，考察太阳辐射强度、风速、路面结构等因素对热边界底部温度增量的影响。最后，对各影响因素及其交互作用下的热边界底部温度增量进行二次正交回归分析，建立热边界底部温度计算模型，并以青藏高原气象数据和青藏高速公路路基试验段实测的温度验证模型的可靠性。研究结果表明：热边界厚度与路基等效热扩散率线性正相关；路面吸收率对热边界底部温度增量的影响最大，太阳辐射强度的影响次之，对流换热系数的影响中等，等效热扩散率的影响较小，发射率的影响最小；该模型可靠性高，可以用来预测路基热边界。

附面层；热边界；敏感性分析；正交分析法；预测模型

与天然地表相比，沥青路面具有强烈的吸热作用和较弱的蒸发作用[1]。沥青路面因显著的温度敏感性常常会产生车辙、推移、拥包等现象。在多年冻土区，沥青路面的这种强吸热性会造成路基下方多年冻土融化、上限下移，进而引发路基下沉、路面开裂、凹陷等病害，严重影响行车安全[2−4]，可见，温度对路基热稳定性有显著的影响。路基温度场模拟是研究路基热稳定性的基础，而路基热边界条件的确定是路基温度场分析的关键[5]。路基热边界是路表与外界环境能量交换的结果，许多学者采用能量平衡法进行估算[5−7]。但受太阳辐射强度、风速、大气温度等气象条件和路面吸收率、反射率、导热系数、比热容等路面结构热物理参数的综合影响，对路基温度场进行长期模拟时，要精确确定路基热边界相当困难。目前，对寒区工程热边界的处理方法主要如下3种：一是现场实测温度，如冻土工程国家重点实验室在青藏铁路沿线布设37个测温孔，其中多年冻土区30个，融区6个，季节冻土区1个[8]。这种方法受限于测温孔以地温监测为主，往往不能确定路表的温度并且测温传感器容易失效。二是理论分析加数值模拟方法，这种分析方法根据传热学原理，将热边界作为隐含量，视大气、土体为整体系统，来分析路基温度场[9−12]。这种方法需要详细的气象、地质资料，在工程应用时需确定的参数较多，会有诸多不便。三是统计分析研究，即利用气象统计资料，分析建立路基表面温度与大气温度等因素间的关系，以此来研究温度场[13−15]。这种方法需要对大量的气象数据进行统计分析，并且统计结果带有一定的区域局限性，同时，这种分析方法不考虑气象条件和路面结构热物理参数各因素间的交互作用，所得经验公式误差相对偏大。朱林楠[16]经过长期的气候及地温观测，将流体力学中的附面层概念引入岩土工程，提出了路基温度场计算的“附面层理论”。该理论定义路表上下一定范围内温度、湿度受大气及太阳辐射作用强烈的物理层为“附面层”，附面层底部温度受太阳辐射、地面紊流热交换等因素影响较小，以致可以忽略，进而建立了附面层温度与大气温度之间的经验关系，即附面层底部温度等于大气平均温度加上1个温度增值。附面层理论可用于有效地分析路基温度 场[17−19]，但在应用时存在如下问题，1) 对附面层厚度的确定没有统一标准；2) 附面层底部温度均以现场实测地温为依据，通过函数拟合得到，这在温度场分析时极为不便；3) 附面层理论虽然对附面层厚度和附面层底部温度的确定给出了相应的算法，但对其中参数的确定缺少理论分析和科学依据，实际应用时无法直接采用模型计算。为此，本文作者基于附面层理论，综合考虑影响路面温度场的气象条件和路面结构热物理参数各因素，建立路面结构热交换计算模型；以附面层厚度作为路基热边界厚度，以附面层底部温度作为热边界底部温度，通过数值模拟和灰关联分析，考察太阳辐射强度、风速、路面结构等因素对热边界底部温度增量的影响，经理论分析，选用合适的判据给出热边界厚度的确定方法，并利用二次正交回归对太阳辐射强度、风速、大气温度等气象条件和路面吸收率、反射率、导热系数、比热容等路面结构热物理参数交互变化时的热边界底部温度增量进行研究，构建可以有效预测路基热边界条件的模型，为路基热边界的确定提供合理依据。

1 路面结构热交换计算模型

由于沥青材料的小孔隙度阻碍路基面层下方水分的蒸发过程，路基表层不能形成有效的湍流散热[20]。降雨、降雪对地表能量传输的影响主要体现在地表反照率的变化方面，反照率的变化主要受地面持水性和入渗特性的影响，与天然地表相比，沥青路面具有低孔隙度和低渗透性，其反照率是天然地表的30%左 右[21]。沥青路面的强吸热作用会使路面积雪保存时间较短。鉴于上述原因，沥青路面结构传热分析时，忽略水汽蒸发耗热和降雨、降雪的影响。路面与周围环境热交换过程主要包括热传导、对流和辐射。

1.1 辐射换热

路表与环境的辐射换热过程包括路表吸收的太阳辐射S和路表反射的长波辐射F。考虑到大气对太阳辐射的反射作用，路表实际吸收的太阳辐射S表示为

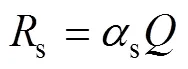
式中：为参数，=12/0，0为实际有效日照时间；0为太阳日辐射强度最大值，0=0.131d，d为太阳日辐射总强度，为角频率，=2π/24；为时间。

路表向外发射的长波辐射F可以表示为[23]

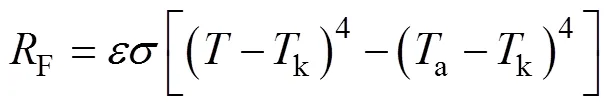
式中：为路面发射率；为玻尔兹曼常数；为路表温度；k为绝对零度；a为大气温度。大气温度的日变化可以表示为

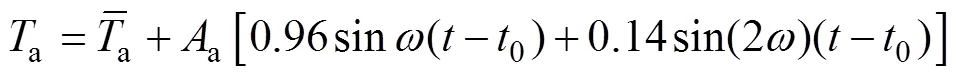
1.2 对流换热

空气对流带给路表的热量可以表示为

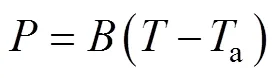
式中：为对流换热系数，W/(m2·℃)。按照经验公式，其与风速的关系为[23]

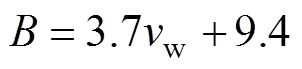
式中：w为日平均风速，m/s。

1.3 热传导

路基内的热传导问题实际是路基面层、基层和土基等各层组成的层状结构的温度场问题。假设路基层间接触良好，热阻为0，路基内热传导方程表示为

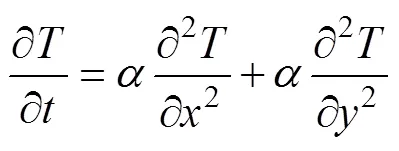
根据能量守恒原理，该问题的有限元计算公式 为[24]

1.4 路面温度场有限元模型

以某路段实际路面结构和材料情况为路面温度场的计算模型，路基结构从上至下依次为改性沥青、重交沥青、水泥稳定碎石基层、石灰土和土基层，各层厚度如图1所示。路基各层材料热物理参数与气象数据皆采用文献[25]中实测值，如表1所示，当地太阳辐射强度、风速及气温等气象数据如表2所示。采用ANSYS有限元软件建立该路段路基传热模型，模型中沥青路面太阳辐射吸收率取0.9，路面反射率取0.81，下边界热通量温度梯度取0.03℃/m[25]，即热流取 37.5 mW/m2。

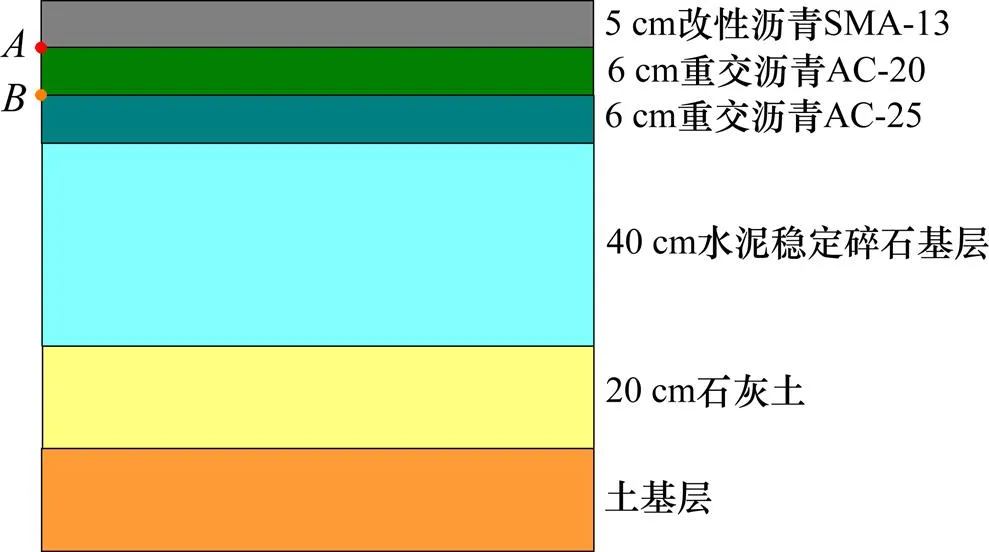
图1 路面结构示意图

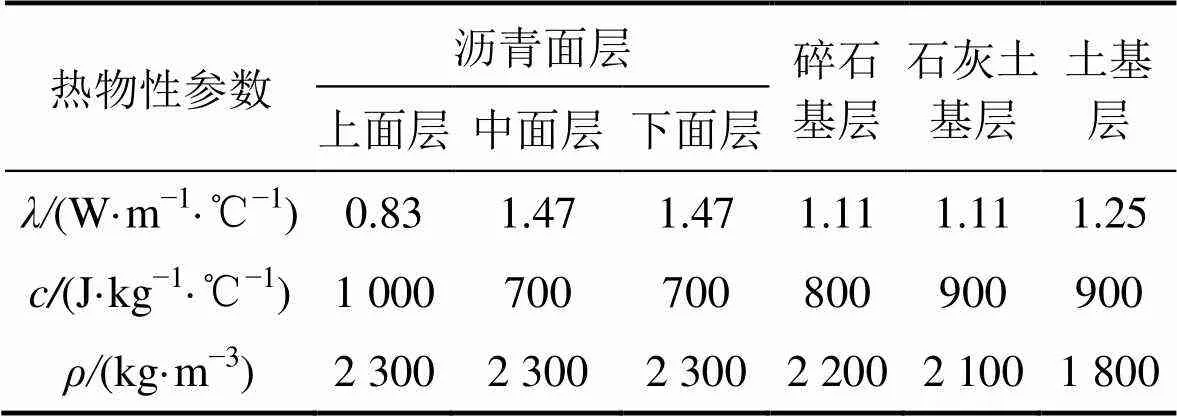
表1 路面结构各层材料热物性参数

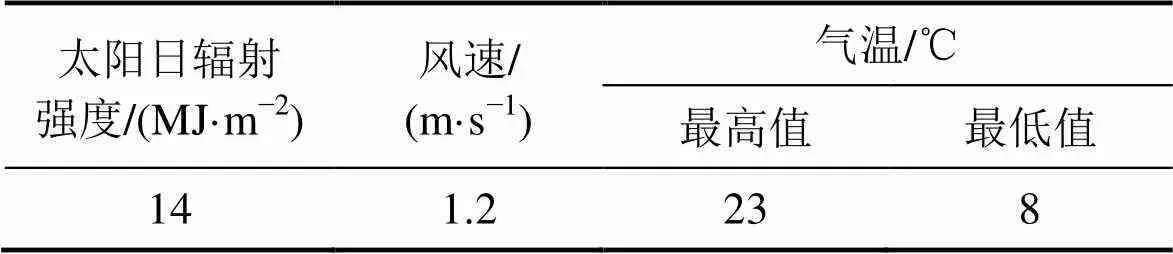
表2 当地气象参数

1.5 计算结果验证

取计算结果中重交沥青AC-20上层点和下层点(图1)温度计算值与实测值进行比较，结果如图2所示。从图2可以看出，点和点温度的计算值较实测值均有不同程度的滞后，在升温阶段，滞后性更明显，而在降温阶段滞后性较好，这主要是由于模型计算时，没有考虑路基内的蒸发换热过程。模型温度计算值与实测值总体变化趋势一致，尤其是下层点的计算值与实测值很吻合，证明参数的选取和模型的建立是正确的。

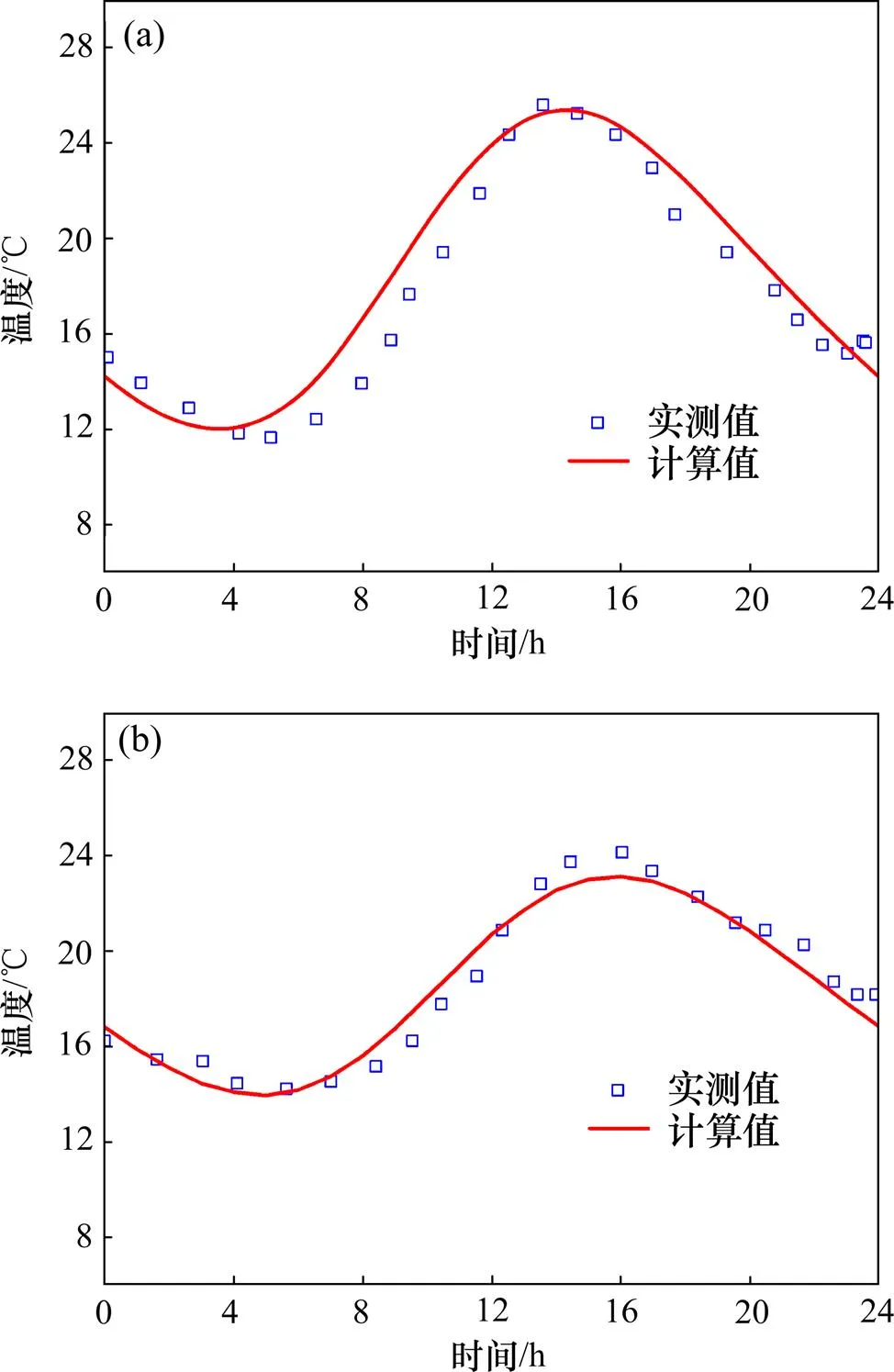
(a) 中面层上部A点温度；(b) 中面层下部B点温度

2 路基温度场热边界厚度的确定

假设路基为半无限体，在周期性变化的热边界条件作用下，路基温度场的解析解为[26]

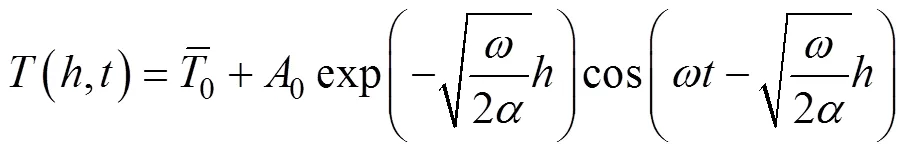
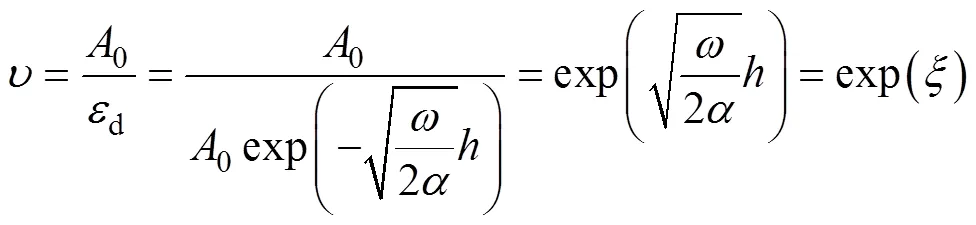
式中：为路基热传导衰减指数。

由于路基的热传导实质是路基面层、基层和土基等各层组成的层状结构的温度场问题，则温度振幅经过多层路基材料的总衰减度可以表示为各层路基结构衰减度叠加的形式：

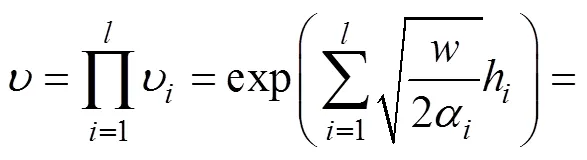
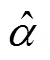
根据热−质交换特点和温度变化连续性，路基表面至浅层地表划分为对流换热区、辐射换热区和热传导换热区，其中，辐射换热区分为上附面层(与空气衔接)和下附面层(与土介质衔接)[16]。在路基某一深度处，大气温度和太阳辐射强度的日波动对地温振幅的影响很小，可以忽略，则定义该深度为附面层底部，其厚度为f，以此作为热边界厚度。热边界底部温度变化可以表示为

式中：T为热边界底部温度相对大气平均温度的增值；f为热边界温度的振幅；为初相。

考虑到热边界底部，太阳辐射对地温的影响较小，本文采用文献[27]中标准对热边界的位置进行确定：

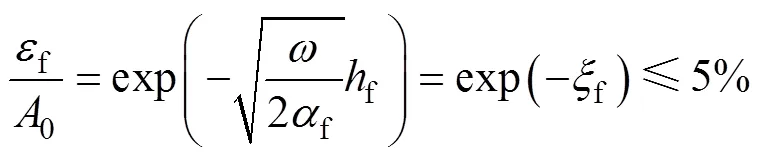
通过式(14)确定热边界底部的热传导衰减指数f，然后假定热边界底部位于多层路面结构体系的第层，并利用式(15)确定第层的位置：

当热边界位于路面结构体系的第层时，根据路基结构中热传导的衰减，采用如下方法确定热边界厚度：

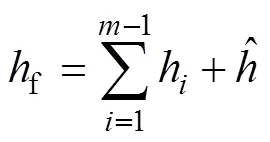
热边界厚度因路基填料不同而异，沥青面层的等效热扩散率为4.3×10−7~8.7×10−7m2/s[28]，分别计算不同等效热扩散率沥青路面的热边界厚度，如图3所示。由图3可以看出：热边界厚度与等效热扩散率具有很好的正相关性，并且热边界厚度的理论解析值和数值计算值吻合较好，说明通过式(16)计算热边界厚度是可行的。

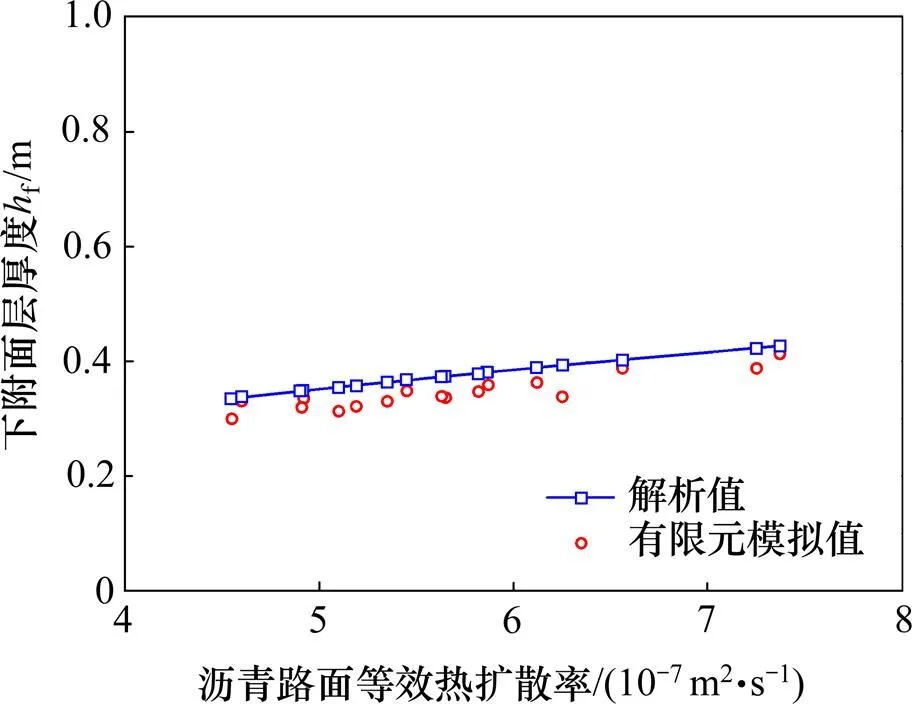
图3 沥青路面等效热扩散率与热边界厚度hf之间的关系

Fig. 3 Relationship between equivalence thermal diffusivity and thermal boundary layer thickness

3 路面温度场影响因素敏感性分析

根据前述分析，给出了确定路基热边界位置的方法，而辐射强度、大气温度、风速等外部气象因素和路面吸收率、反射率、导热系数、比热容等路面结构热物理参数会对热边界底部温度增量T产生影响。采用灰关联分析法，以灰关联度作为衡量标准，分析影响热边界底部温度增量的各因素的敏感性。

3.1 灰关联分析原理

以热边界底部温度增量的各影响因素为比较列，记作

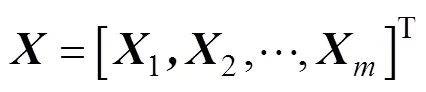
以各影响因素相应的温度增量为参考列，记作

其中：与列每项各有若干取值；X[x1，x2，…，x]；Y[y1，y2，…，y]。采用初值化、均值化、区间相对值化和归一化等方法对X和Y的数值进行归一化处理：

采用下式得到差异序列矩阵，在差异序列矩阵中找出最大值max和最小值min：

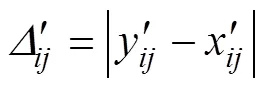
关联系数V表示比较因素和参考因素的相关性：

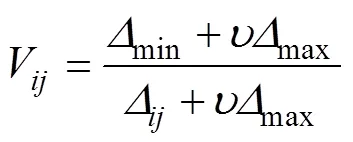
式中：为分辨系数，用来提高关联系数间差异的显著性，∈[0,1]，一般取0.5。

对关联系数求平均值得到关联度A，影响因素的关联度越大，说明该因素对目标影响越大，其敏感性越大。

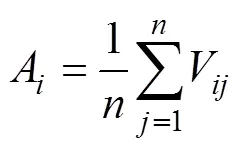
3.2 各因素敏感性分析

影响热边界底部温度增量的各因素的合理取值如表3所示。分别计算路面吸收率、发射率、太阳辐射强度、对流换热系数和等效热扩散率对热边界底部温度增量T的影响，计算结果如图4所示。由图4可以看出：吸收率、对流换热系数和太阳辐射强度对热边界底部温度增量的影响较大。吸收率与温度增量成线性正相关，这与吸收率本身的物理含义一致，当吸收率从0.50变到0.91时，温度增量变化将近1.5 ℃。发射率与温度增量成线性负相关，这是因为发射率越大，路面向外的辐射能力越强，释放的热能就越多。当发射率在合理范围内变化时，温度增量减小0.355 ℃，这比吸收率对温度增量的影响要小很多.这是因为路面对太阳辐射的吸收主要是对短波辐射的吸收，而路面本身对外辐射属于长波辐射，在同等条件下，短波辐射能量大于长波辐射能量。太阳辐射强度与温度增量的关系成线性正相关，当该因素在合理范围内变化时，温度增量变化很明显，这是由于太阳辐射强度直接决定进入路基的热量，也直接影响路基温度场。对流换热系数与温度增量呈幂函数关系，总体来说，温度增量随换热系数的增大逐渐减小，递减速率由大变小，在导热系数合理取值范围内温度增量减小3.457 ℃。对流换热系数越大说明单位面积路面与环境交换热能的能力越强，而这种换热能力又受风速和路面粗糙度等的影响，风速会受近地表气压影响，随着换热的进行，近地表气压发生变化，换热系数也会相应变化。等效热扩散率是对路面结构的综合反映，温度增量随等效热扩散率增大而线性减小，取值在合理范围内变化时，温度减小0.384 ℃。对图4中给出的不同影响因素对应的热边界底部温度增量T进行统计回归，得到的回归方程见表4。

表3 各影响因素取值范围

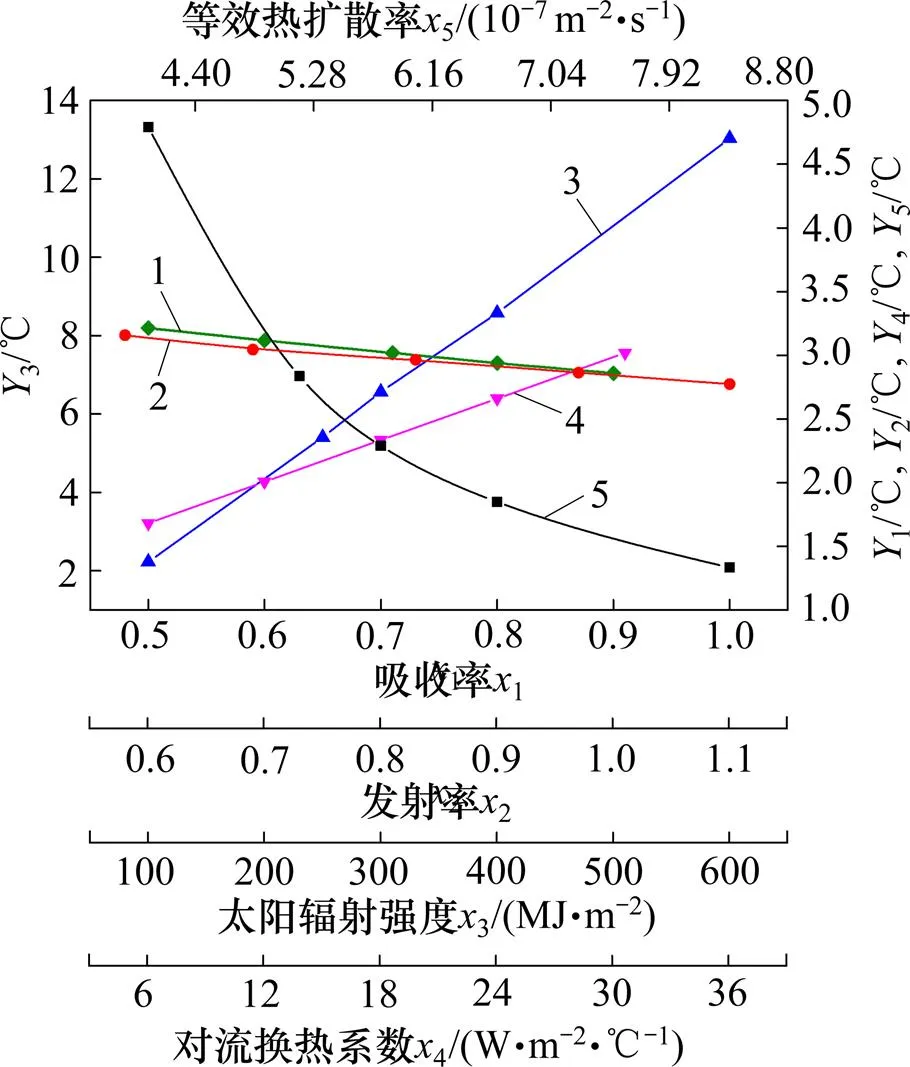
1—发射率；2—等效热扩散率；3—太阳有效辐射强度；4—吸收率；5—对流换热系数。

根据敏感性分析方法，将不同的路面吸收率、发射率、太阳辐射强度、对流换热系数和等效热扩散率以及计算得到的热边界底部温度增量T代入式(17)和(18)中，得

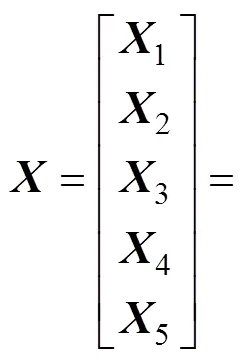
表4 热边界底部温度增量与各影响因素回归方程

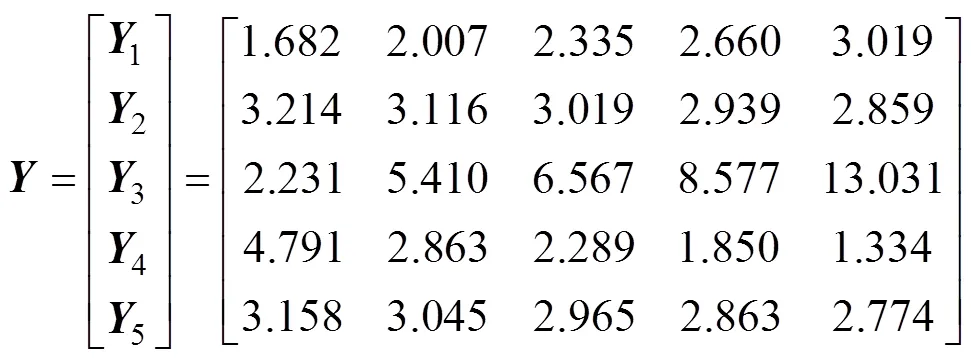
式中：1，2，3，4和5分别为路面吸收率、路面发射率、太阳辐射强度、对流换热系数和等效热扩散率，1，2，3，4和5为该因素对应的热边界底部温度增量值。

对式(23)和(24)进行矩阵归一化、差异矩阵计算等，最终求得关联度：

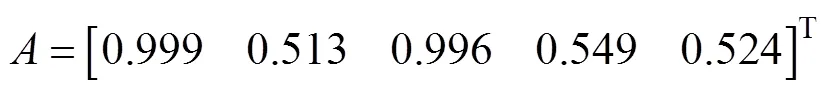
由关联度可以看出，影响热边界底部温度增量的5个因素的敏感性由大到小依次为路面吸收率、太阳辐射强度、对流换热系数、等效热扩散率和发射率。

4 温度增量的二次正交回归分析

为建立有效预测热边界条件的模型，采用二次回归正交分析法对热边界底部温度增量进行研究，以此建立有效预测热边界条件的模型。

4.1 因素水平编码

温度增量在路面吸收率1、发射率2、太阳辐射强度3、对流换热系数4和等效热扩散率5交互作用下变化规律的研究采用二次正交回归分析方法，设置因素水平，见表5。

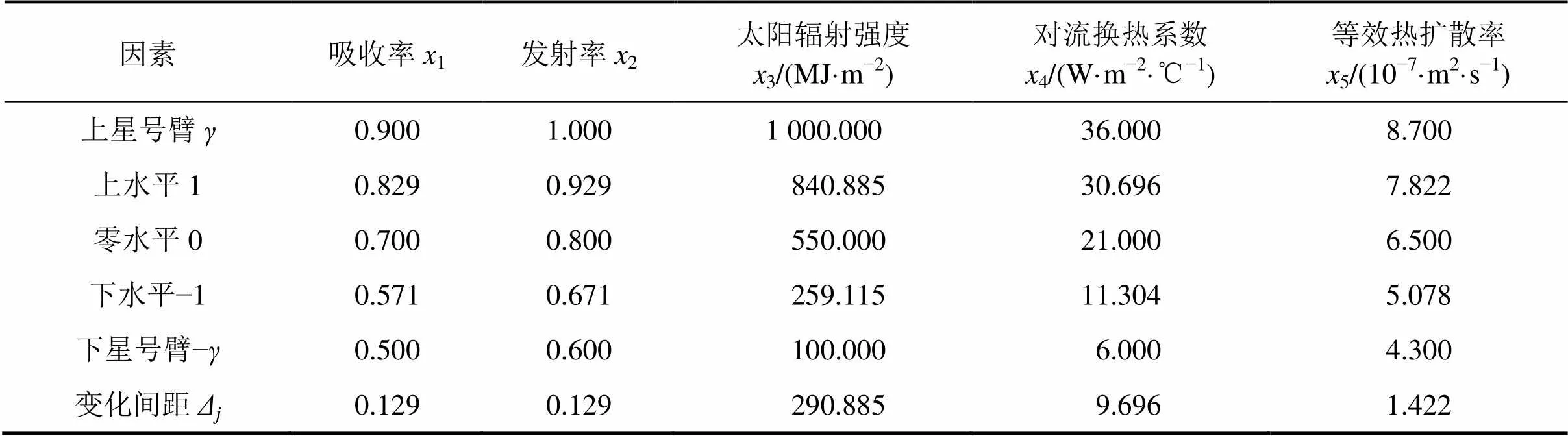
表5 因素水平表

表5中x代表试验中各因素的实际取值，x(=1,2,3,4,5)可按式(26)换算成与其相应的编码值z：

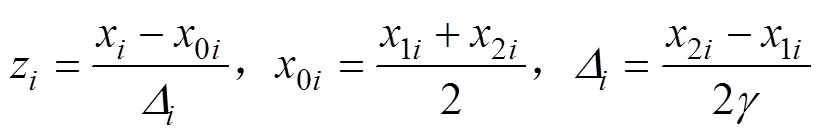
式中：[1i,2i]为第个因素的变化范围；0i为第个因素的上下水平均值；Δ为第个因素的变化间距；为星号臂长度，依据二次正交设计确定，文中取1.547。

4.2 回归正交试验结果

根据二次回归正交设计原理[35]，采用L16(215)正交表进行正交回归分析，因素水平编码值的回归方程如式(27)，二次回归方差分析表见表6。

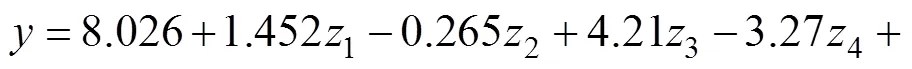
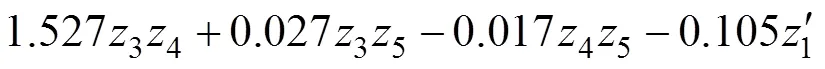
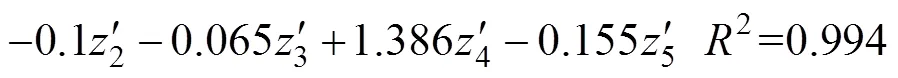
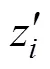
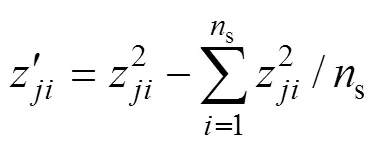
式中：1, 2, …,m，为因素数；1, 2,…,s；s为样本总数。

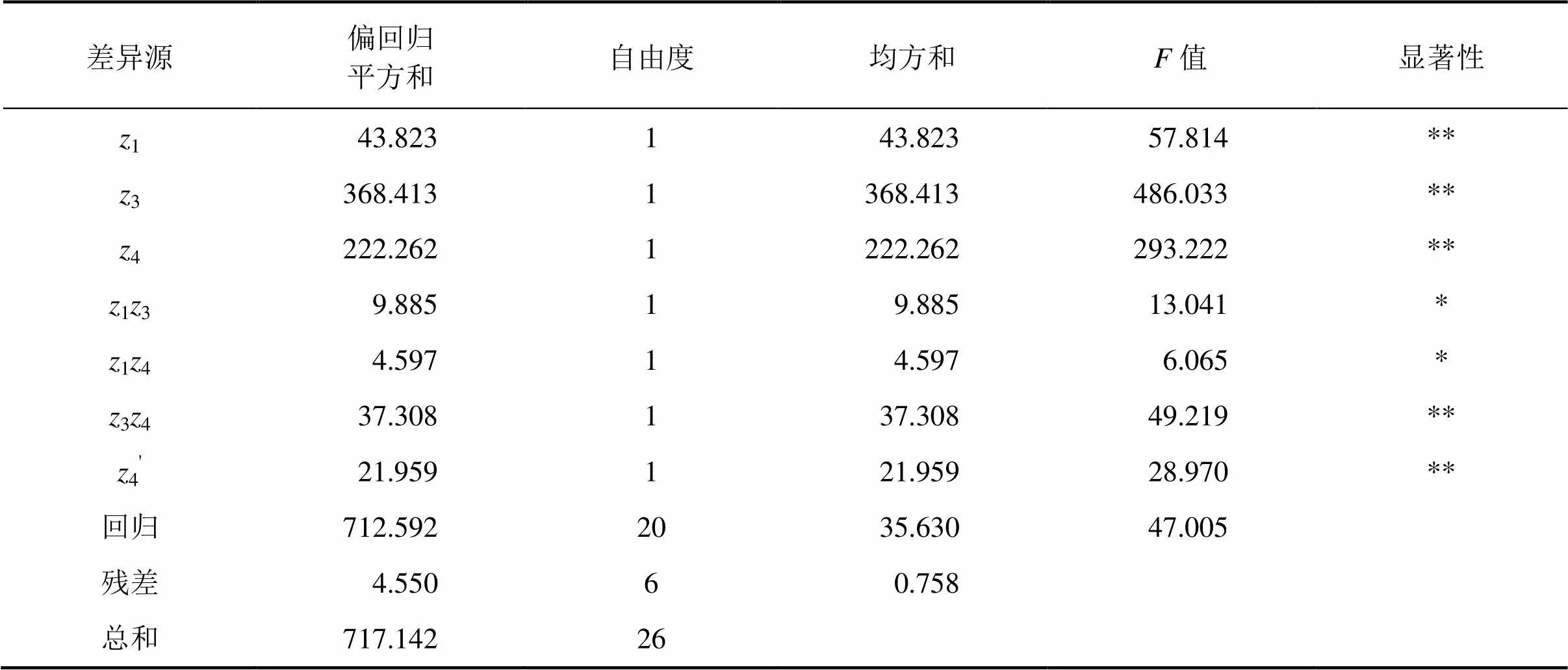
表6 方差分析表 I

注：0.05(1,6)=5.99；0.01(1,6)=13.7；**表示回归系数达到非常显著水平；*表示回归系数达到显著水平；表中省去了未达到显著水平的方差分析值。

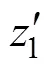
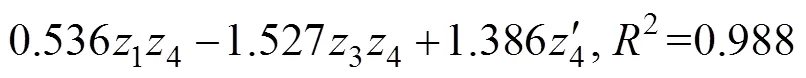
由表7可知：0.05(7,19)=2.54＜216.192，回归方程达到显著水平，方程有意义。由表7可以看出各回归系数均达到显著水平，为不显著因素对其余7个显著因素所产生的影响，构造新的统计量：

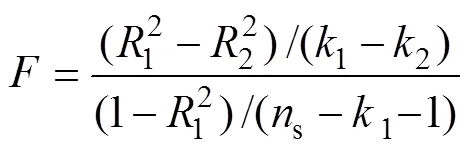
式中：1和2分别为修正前后因素水平编码值回归方程的相关系数；1和2分别为修正前后因素水平编码值回归方程的自变量个数；值服从自由度为1−2和s−1−1个自由度的分布。根据前文中的计算值得=0.38<0.05(13,5)=3.03，则在给定的显著水平=0.05下，所删除的未达到显著性的因素对方程不造成显著性影响。

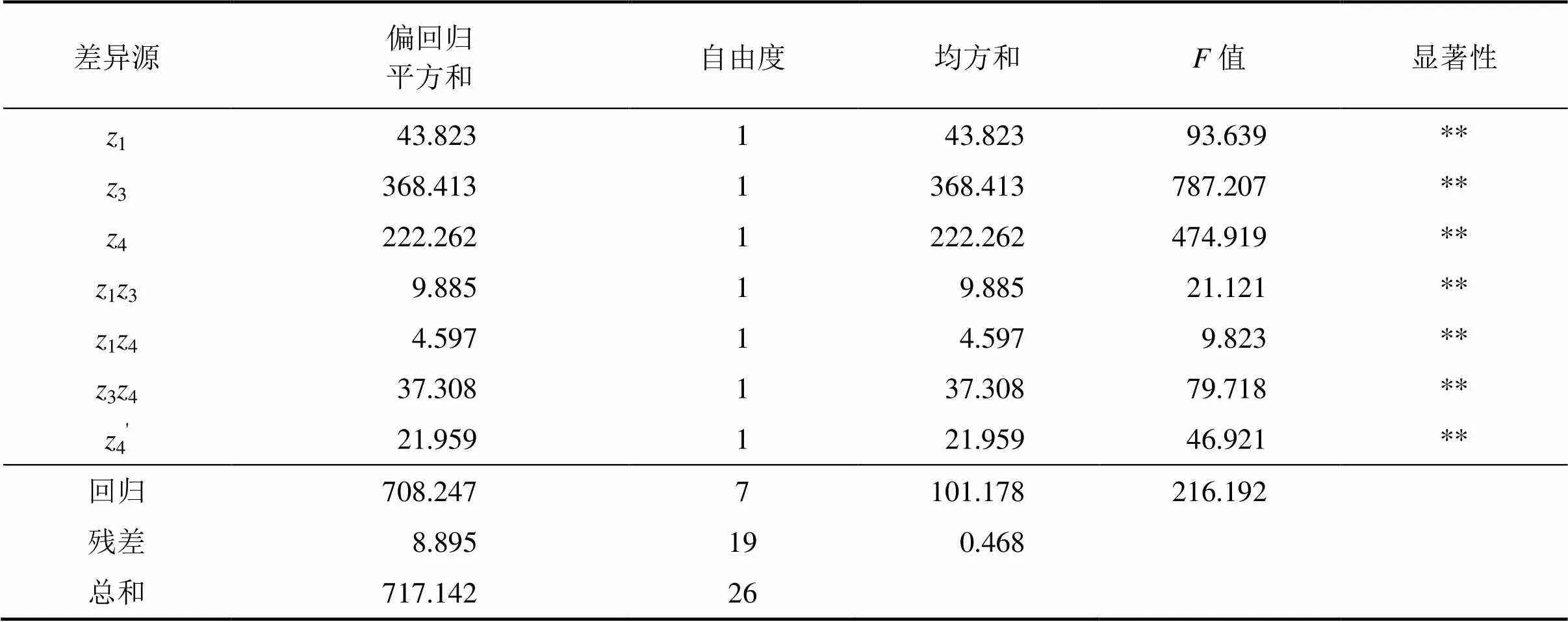
表7 方差分析表 II

注：0.05(1,19)=4.38；0.01(1,19)=8.18；**表示回归系数达到非常显著水平；*表示回归系数达到显著水平。

由式(29)可得因素实际值温度增量方程：

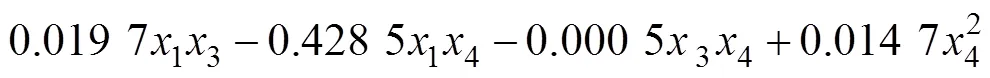
式中：i(=1，2，3，4，5)分别代表实际路面吸收率、路面发射率、太阳辐射强度、对流换热系数和等效热扩散率的取值。

5 热边界条件预测模型

5.1 热边界条件预测模型

以式(13)作为路基温度场长期模拟的热边界温度，考虑到热边界底部温度振幅可以忽略，另外，大气平均气温为年波动函数，一般以周期为1 a的正弦函数表示，路基温度场长期模拟时的热边界条件预测模型为

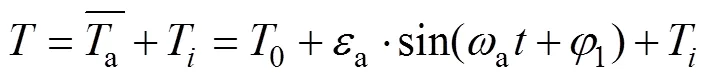
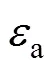
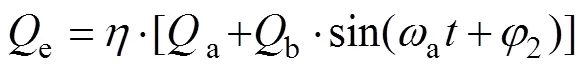
式中：为坡面系数，其值可根据路面实际情况参考文献[36]得到；e为太阳日辐射总强度；a和b分别为太阳辐射强度的年平均值和年振幅，其值按实测太阳辐射强度拟合；2为太阳辐射强度函数的初相位；4(对流换热系数)可通过现场实时监测的风速，按式(7)计算得到。风速由于受大气环流和下垫面异常的影响较大，其季节波动性很强，区域差异较大，随着全球气候变暖，我国年平均风速呈现不同程度的降低趋 势[37−38]，为此采用如下方法处理风速：

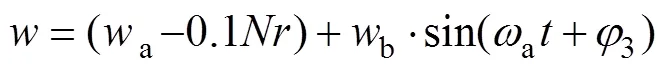
式中：a为年平均风速；为路基温度场长期模拟年限；为年平均风速每10年的降低速率，其值根据路基所处风速区采用文献[38]得到；b为风速年振幅；3为风速函数的初相位。

5.2 预测模型验证

为了验证预测模型的适用性，取青藏高原北麓河地区路基试验段现场监测温度和气象数据对模型进行验证。日平均气温、太阳有效日辐射及按实测风速计算得到热交换系数的实测值和拟合值分别如图5~7所示。热边界条件预测所需参数见表8。

将各因素取值和气温平均值代入式(31)和(32)计算，可得模型预测值，如图8所示。从图8可以看出模型预测值与实测值较吻合，说明热边界预测模型具有适用性。

图5 太阳有效日辐射实测值与拟合值

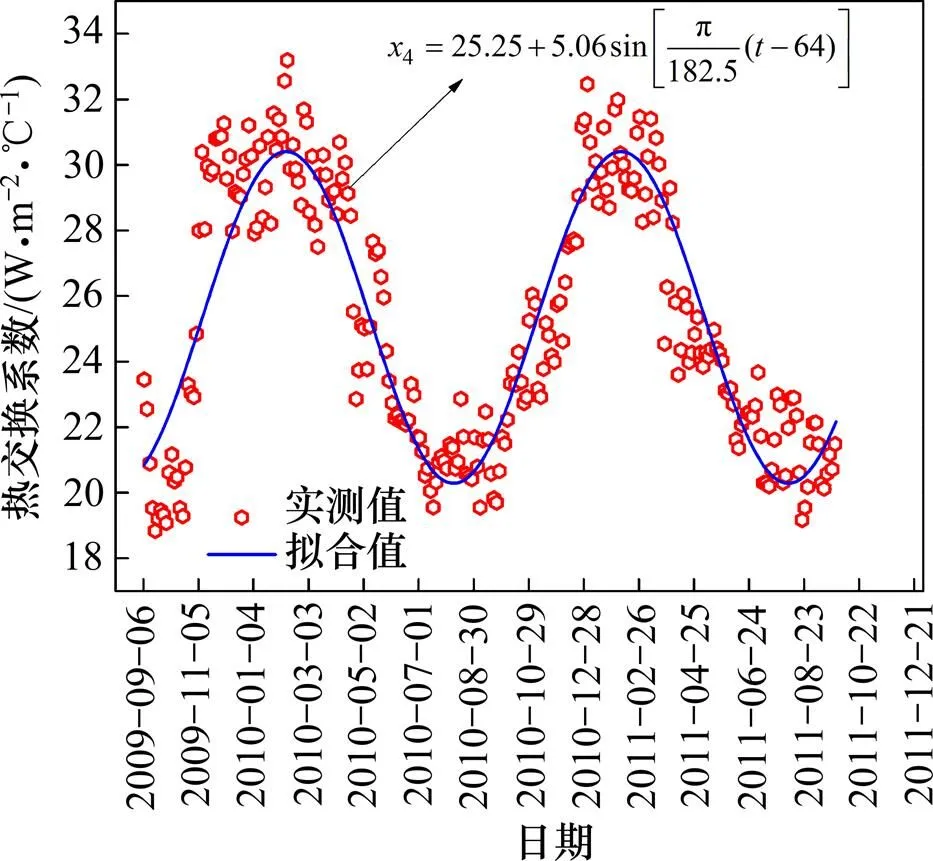
图6 对流换热系数实测值与拟合值

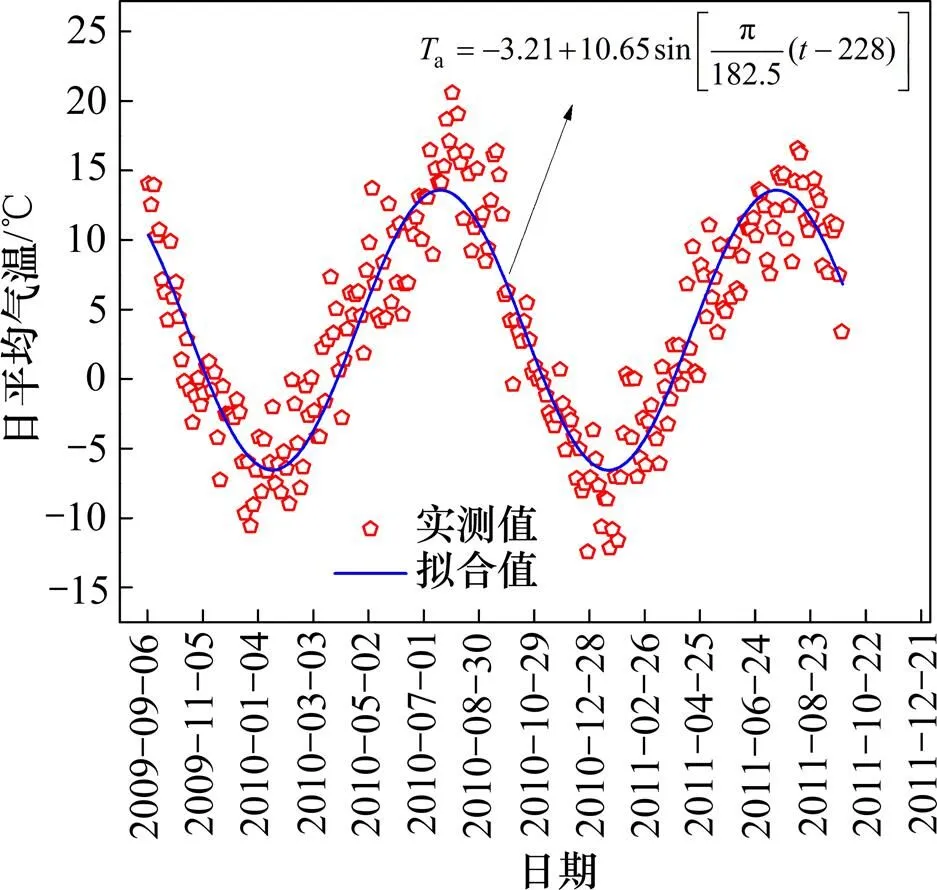
图7 日平均气温实测值与拟合值

表8 预测模型参数取值

图8 热边界底部温度实测值与计算值

6 结论

1) 路基温度场的热传递过程包括辐射、对流和热传导，是外部因素(太阳辐射强度、气温、对流换热系数)和内部因素(路面吸收率、发射率、路面结构)综合作用的结果，通过理论分析，给出了路基热边界条件的确定方法。热边界厚度与路基等效热扩散率线性正相关。热边界底部温度增量与路面吸收率、太阳辐射强度、等效热扩散率线性正相关；与路面发射率线性负相关；与对流换热系数成负指数相关。

2) 通过灰关联方法分析热边界底部温度增量各影响因素的敏感性，表明路面吸收率对热边界底部温度增量的影响最大，太阳辐射强度的影响次之，对流换热系数的影响中等，等效热扩散率的影响较小，发射率的影响最小。减小吸收率可以显著降低热边界底部温度增量，增大发射率也可以起到降低温度增量的作用，但影响小于降低吸收率。

3) 基于二次正交回归分析理论建立了热边界条件与太阳辐射强度、气温、对流换热系数、路面吸收率、发射率、等效热扩散率的函数关系。通过现场气象和地温监测资料对该模型适用性进行了验证，为预测路基热边界条件提供了技术支撑。

[1] 王绍令, 赵林, 李述训, 等. 青藏公路多年冻土段沥青路面热量平衡及路基稳定性研究[J]. 冰川冻土, 2001, 23(2): 111−118. WANG Shaolin, ZHAO Lin, LI Shuxun, et al. Study on thermal balance of asphalt pavement and roadbed stability in permafrost regions of the Qinghai-Tibet highway[J]. Journal of Glaciology and Geocryology, 2001, 23(2): 111−118.

[2] 窦建明, 胡长顺, 何子文, 等. 青藏公路多年冻土段路基病害分布规律[J]. 冰川冻土, 2002, 24(6): 780−783. DOU Mingjian, HU Changshun, HE Ziwen, et al. Distributing regularities of subgrade diseases in permafrost section of the Qinghai-Tibet highway[J]. Journal of Glaciology and Geocryology, 2002, 24(6): 780−783.

[3] 张鲁新, 原思成, 杨永平. 青藏铁路多年冻土区路基变形裂缝发生机理及其防治[J]. 第四纪研究, 2003, 23(6): 604−610. ZHANG Luxin, YUAN Sicheng, YANG Yongping. Mechanism and prevention of deformation cracks of embankments in the permafrost region along Qinghai-Xizang railway[J]. Quaternary Sciences, 2003, 23(6): 604−610.

[4] 俞祁浩, 谷伟, 钱进, 等. 多年冻土区高等级公路建设面临问题分析[J]. 公路, 2010, 11(11): 74−80. YU Qihao, GU Wei, QIAN Jin, et al. Problem analysis of high grade highway construction in permafrost regions[J]. Highway, 2010 , 11(11): 74−80.

[5] ZHANG Mingyi, LAI Yuanming, GAO Zhihua, et al. Influence of boundary conditions on the cooling effect of crushed-rock embankment in permafrost regions of Qinghai-Tibetan Plateau[J]. Cold Regions Science and Technology, 2006, 44(3): 225−239.

[6] ZHANG T, OSTERKAMP T E, STAMNES K. Influence of the depth hoar layer of the seasonal snow cover on the ground thermal regime[J]. Water Resources Research, 1996, 32(7): 2075−2086.

[7] ZHANG T, STAMNES K. Impact of climatic factors on the active layer and permafrost at Barrow, Alaska[J]. Permafrost and Periglacial Processes, 1998, 9(3): 229−246.

[8] 穆彦虎. 青藏铁路冻土区路基温度和变形动态变化过程研究[D]. 兰州: 中国科学院寒区旱区环境与工程研究所, 2012: 24−34. MU Yanhu. Analyses on dynamic variations of embankment thermal regime and deformation along the Qinghai-Tibet Railway in permafrost regions[D]. Lanzhou: The Chinese Academy of Sciences. Cold and Arid Regions Environmental and Engineering Research Institute, 2012: 24−34.

[9] 王可丽, 程国栋.青藏铁路沿线地表和路基表面热力学模式(Ⅰ): 物理过程与实验方案[J]. 冰川冻土, 2002, 24(6): 759−764. WANG Keli, CHENG Guodong. Thermodynamic model of the ground surface and the roadbed surface along the Qinghai-Tibetan Railway (Ⅰ): physical process and experimental scheme[J]. Journal of Glaciology and Geocryology, 2002, 24(6): 759−764.

[10] 王可丽, 程国栋, 江灏, 等. 青藏铁路沿线地表和路基表面热力学模式(Ⅱ): 无云大气条件下模拟试验结果分析[J]. 冰川冻土, 2004, 26(2): 171−176. WANG Keli, CHENG Guodong, JIANG Hao, et al. Thermodynamic model of the ground surface and embankment surface along the Qinghai—Tibet Railway (Ⅱ): results in the cloud-free condition[J]. Journal of Glaciology and Geocryology, 2004, 26(2): 171−176.

[11] 江灏, 吴青柏, 王可丽, 等. 青藏铁路沿线地表和路基表面热力学模式(Ⅲ): 参数化方案[J]. 冰川冻土, 2005, 27(5): 680−685. JIANG Hao, WU Qingbai, WANG Keli, et al. Thermodynamic model of the ground surface and embankment surface along the Qinghai—Tibet Railway (Ⅲ): parameterization schemes[J]. Journal of Glaciology and Geocryology, 2005, 27(5): 680−685.

[12] LIU Zhiyun, CHEN Jianbing, JIN Long, et al. Roadbed temperature study based on earth-atmosphere coupled system in permafrost regions of the Qinghai—Tibet Plateau[J]. Cold Regions Science and Technology, 2013, 86(2): 167−176.

[13] 张文纲, 李述训, 吴通华, 等. 青藏高原地气温差变化分析[J]. 地理学报, 2006, 61(9): 899−910. ZHANG Wengang, LI Shuxun, WU Tonghua, et al. Changes of the differences between ground and air temperature over the Qinghai—Xizang Plateau[J]. Acta Geographica Sinica, 2006, 61(9): 899−910.

[14] 李述训, 吴通华. 青藏高原地气温度之间的关系[J]. 冰川冻土, 2005, 27(5): 627−632. LI Shuxun, WU Tonghua. The relationship between air temperature and ground temperature in the Tibetan Plateau[J]. Journal of Glaciology and Geocryology, 2005, 27(5): 627−632.

[15] KARUNARATNE K C, BURN C R. Relations between air and surface temperature in discontinuous permafrost terrain near Mayo, Yukon Territory [J]. Canadian Journal of Earth Sciences, 2004, 41(12): 1437−1451.

[16] 朱林楠. 高原冻土区不同下垫面的附面层研究[J].冰川冻土, 1988, 10(1): 8−14. ZHU Linnan. Study of the adherent layer on different types of ground in permafrost regions on the Qinghai-Xizang Plateau[J]. Journal of Glaciology and Geocryology, 1988, 10(1): 8−14.

[17] ZHANG Mingyi, LAI Yuanming, DONG Yuanhong. Numerical study on temperature characteristics of expressway embankment with crushed-rock revetment and ventilated ducts in warm permafrost regions[J]. Cold Regions Science & Technology, 2009, 59(1): 19−24.

[18] 赵世运. 青藏铁路冻土区“冷却地基”设计理论的研究和实 践[D]. 兰州: 中国科学院寒区旱区环境与工程研究所, 2007: 173−209. ZHAO Shiyun. The study and practice of cooling embankment in permafrost regions of Qinghai-Tibet Railway[D]. Lanzhou: The Chinese Academy of Sciences. Cold and Arid Regions Environmental and Engineering Research Institute, 2007: 173−209.

[19] 孙志忠. 青藏铁路多年冻土区块石护坡路基试验研究[D]. 兰州: 中国科学院寒区旱区环境与工程研究所, 2006: 90−105. SUN Zhizhong. Study on the crushed-rock revetment embankment in permafrost regions of Qinghai—Tibet Railway[D]. Lanzhou: The Chinese Academy of Sciences. Cold and Arid Regions Environmental and Engineering Research Institute, 2006: 90−105.

[20] ASAEDA T, CA V T, WAKE A. Heat storage of pavement and its effect on the lower atmosphere[J]. Atmospheric Environment, 1996, 30(3): 413−427.

[21] 张中琼. 多年冻土区沥青路面热效应机理研究[D]. 兰州: 中国科学院寒区旱区环境与工程研究所, 2012: 25−30. ZHANG Zhongqiong. Study on the mechanism of asphalt pavement’s thermal effects in permafrost regions[D]. Lanzhou: The Chinese Academy of Sciences. Cold and Arid Regions Environmental and Engineering Research Institute, 2012: 25−30.

[22] 严作人. 层状路面体系的温度场分析[J]. 同济大学学报(自然科学版), 1984, 16(3): 79−88. YAN Zuoren. Analysis of the temperature field in layered pavement system[J]. Journal of Tongji University(Natural Science), 1984, 16(3): 79−88.

[23] 王孙富. 沥青路面结构温度场与温度应力的数值模拟分析[D]. 哈尔滨: 哈尔滨工业大学交通科学与工程学院, 2010: 15−16. WANG Sunfu. Simulation analysis of temperature field and thermal stress for bituminous pavement structure[D]. Harbin: Harbin Institute of Technology. School of Transportation Science and Engineering, 2010: 15−16.

[24] 张朝晖. ANSYS热分析教程与实例解析[M]. 北京: 中国铁道出版社, 2007: 51−52. ZHANG Chaohui. ANSYS thermal analysis tutorial and case analysis[M]. Beijing: China Railway Press, 2007: 51−52.

[25] 冯德成, 胡伟超, 于飞, 等. 沥青路面材料热物性参数对温度场的影响及敏感性分析[J]. 公路交通科技, 2011, 28(11): 12−19. FENG Decheng, HU Weichao, YU Fei, et al. Impact of asphalt pavement thermophysical property on temperature field and sensitivity analysis[J]. Journal of Highway and Transportation Research and Development, 2011, 28(11): 12−19.

[26] 赵镇南. 传热学[M]. 2版. 北京: 高等教育出版社, 2007: 142−145. ZHAO Zhennan. Heat transfer[M]. 2nd ed. Beijing: Higher Education Press, 2007: 142−145.

[27] 白青波, 李旭, 田亚护. 路基温度场长期模拟中的地表热边界条件研究[J]. 岩土工程学报, 2015, 37(6): 1142−1149. BAI Qinbo, LI Xu, TIAN Yahu. Upper boundary conditions in long-term thermal simulation of subgrade[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(6): 1142−1149.

[28] 张慧彧, 邹玲, 纪小平. 沥青混合料导热系数的试验研究[J]. 公路, 2011(10): 50−51. ZHANG Huiyu, ZOU Lin, JI Xiaoping. Experimental study on the heat conduction of asphalt mixtures[J]. Highway, 2011(10): 50−51.

[29] 陈明宇. 沥青路面太阳能集热性能研究[D]. 武汉: 武汉理工大学材料科学与工程学院, 2010: 22−23. CHEN Mingyu. Research on solar energy collection using asphalt pavement[D]. Wuhan: Wuhan University of Technology. School of Materials Science and Engineering, 2010: 22−23.

[30] 张鑫. 沥青路面热反射与热阻技术降温机理与应用研究[D]. 哈尔滨: 哈尔滨工业大学交通科学与工程学院, 2011: 38−40. ZHANG Xin. Research on heat reflection and thermal resistance technology of asphalt pavement cooling mechanism and its application[D]. Harbin: Harbin Institute of Technology. School of Transportation Science and Engineering, 2011: 38−40.

[31] 翁笃鸣. 中国太阳直接辐射的气候计算及其分布特征[J]. 太阳能学报, 1986, 7(2): 3−12. WENG Duming. Climatical method for direct solar radiation calculation and its distribution over China[J]. Acta Energiae Solaris Sinica, 1986, 7(2): 121−130.

[32] 马有哲, 刘小宁, 许松. 中国太阳辐射数据集及其质量检验分析[J]. 气象科技, 1998(2): 53−56. MA Youzhe, LIU Xiaoning, XU Song. Analysis of data set and quality inspection radiation in China[J]. Meteorological Science and Technology, 1998(2): 53−56.

[33] 吴其重, 王自发, 崔应杰. 我国近20年太阳辐射时空分布状况模式评估[J]. 应用气象学报, 2010, 21(3): 343−351. WU Qizhong, WANG Zifa, CUI Yingjie. Evaluating the solar radiation resources of China in recent 20 years by meteorological model[J]. Journal of Applied Meteorological Science, 2010, 21(3): 343−351.

[34] SHARPLES S. Full sealed measurements of convective energy losses from exterior building surfaces[J]. Building Environment, 1984, 19: 31−38.

[35] WILLIAM D B. 理解回归假设[M]. 余珊珊, 译. 上海格致出版社, 上海出版社, 2012: 20−50. WILLIAM D B. Understanding regression assumptions[M]. YU Shanshan, trans. Shanghai: Truth and Wisdom Press, Shanghai People’s Publishing House, 2012: 20−50.

[36] 王铁行. 多年冻土地区路基计算原理及临界高度研究[D]. 西安: 长安大学公路工程学院, 2001: 19−21. WANG Tiexing. Research on calculation principle and critical height of subgrade in permafrost regions[D]. Xi’an: Chang’ an University. School of Highway Engineering, 2001: 19−21.

[37] 陈练. 气候变暖背景下中国风速(能)变化及其影响因子研究[D]. 南京: 南京信息工程大学大气科学学院, 2013: 14−15.CHEN Lian. Changes and their impact factors of wind speed (energy) over china under the background of climate warming[D]. Nanjing: Nanjing University of Information Science and Technology. College of Atmospheric Science, 2013: 14−15.

[38] 江滢, 罗勇, 赵宗慈, 等. 近50年中国风速变化及原因分析[C]// 中国气象学会2007年年会气候变化分会场论文集. 北京, 2007: 80−89. JIANG Ying, LUO Yong, ZHAO Zongci, et al. Analysis of wind speed changes and causes in China in the past 50 years[C]// Proceedings of the 2007 Annual Conference of the Chinese Meteorological Society on Climate Change. Beijing, 2007: 80−89.

A prediction model on thermal boundary condition of embankment based on boundary layer theory

LUO Xiaoxiao1, 2, YU Qihao1, MA Qinguo3, ZHANG Jianming1

(1. State Key Laboratory of Frozen Soil Engineering, Northwest Institute of Eco-environment and Resources, Chinese Academy of Sciences, Lanzhou 730000, China;2. School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China;3. State Key Laboratory of Subtropical Building Science, South China University of Technology, Guangzhou 510641, China)

Based on the boundary-layer theory, a model for heat exchange of embankment structure was established firstly considering all influence factors including meteorological conditions and thermal physical parameters of pavement structure to determine thermal boundary condition. And then the method to determine the thermal boundary condition was proposed. Secondly, sensitivity analysis of the influencing factors which affect the temperature increment at the thermal boundary was implemented using the method of grey relation. Finally, considering the influences of all factors and their interaction, the quadratic regression orthogonality analysis method was used to study the temperature increment at the thermal boundary. A prediction model on thermal boundary condition was established and verified by the measured temperature of Qinghai—Tibet Highway. The results show that the thickness of thermal boundary has a positive relationship with the equivalence thermal diffusivity of embankment. The road surface absorptivity has the largest influence on the thermal boundary, followed by the solar radiation, with the convective heat transfer coefficient in the middle, the equivalent thermal diffusivity being the next factor, and the road surface emissivity influences the smallest. The model is reliable and can be used to predict the thermal boundary of embankment.

boundary layer; thermal boundary condition; sensitivity analysis; orthogonality analysis method; prediction model

U416.1+68

A

1672−7207(2019)03−0658−11

10.11817/j.issn.1672-7207.2019.03.020

2018−04−09；

2018−08−11

国家科技支撑计划项目(2014BAG05B03)；国家自然科学基金资助项目(41401088) (Project(2014BAG05B03) supported by the National Science and Technology Pillar Program of China; Project(41401088) supported by the National Natural Science Foundation of China)

俞祁浩，博士，研究员，从事冻土路基稳定性研究；E-mail：yuqh@lzb.ac.cn

(编辑 赵俊)