双旋翼无人机串级线性自抗扰控制

张勇，陈增强，张兴会，孙青林，孙明玮



双旋翼无人机串级线性自抗扰控制

张勇1，陈增强1，张兴会2，孙青林1，孙明玮1

(1. 南开大学 计算机与控制工程学院，天津，300350；2. 天津中德应用技术大学，天津，300350)

介绍线性自抗扰控制器(LADRC)和串级线性自抗扰控制器的组成结构，包括线性跟踪微分器、线性扩张状态观测器以及线性误差控制律，并给出各部分的典型算法。为了解决纵列式双旋翼无人机姿态控制系统中欠驱动、多变量、强耦合的控制问题，设计串级线性自抗扰控制器。研究结果表明：所设计的串级线性自抗扰控制器参数少，便于参数整定，能够满足控制精度及快速性的要求，并且具有较强的鲁棒性、抗干扰性能力以及对非线性强耦合系统的解耦能力。

线性自抗扰控制器；串级控制；线性扩张状态观测器；双旋翼无人机；姿态控制

PID控制就是靠目的与实际输出之间的误差来决定消除此误差的控制策略，并不是靠对象的输入输出模型来决定控制策略。因此，只要选择的PID参数使闭环稳定，就能使一类对象达到静态指标。目前，PID控制器在航天控制、运动控制以及其他过程控制应用中，仍然占据着主导地位。然而，科学技术的发展对控制精度和速度的要求，以及对环境变化的适应能力的要求越来越高，经典PID慢慢显露出它的缺点。为了保留PID控制的优点，克服它的缺点，HAN等[1]在20世纪80年代研究出了一种控制策略“自抗扰控制技术”(active disturbance rejection control technique)。自抗扰控制器最突出的特点就是把作用于被控对象的所有不确定因素以及外部扰动都归结为未知扰动，然后，用对象的输入、输出对它进行估计并给予补偿。自抗扰控制器具有响应速度快、控制精度高、抗干扰能力强的特点，因此，在许多理论研究、试验和工程实际中得到了广泛应用。但是HAN等[1]的自抗扰控制器是非线性的，导致控制器的参数众多，使算法实现和参数调节变得复杂。GAO等[2]提出一种线性自抗扰控制器，这种控制器参数少，便于参数调节和算法实现。纵列式双旋翼无人机的特点是具有前、后2副旋翼，与单旋翼无人机相比，具有运载能力强、运输效率高的优点，更加适合重型直升机的构造[3]。但是，由于纵列式双旋翼无人机的旋翼是前、后布置的，这引起了一系列的空气动力学、飞行动力学和结构动力学问题，这些问题远比单旋翼无人机的复杂，相应的分析和设计技术难度也比单旋翼无人机的大。纵列式双旋翼无人机是一个具有6个自由度和2个控制输入的欠驱动系统，具有多变量、强耦合、非线性和对扰动敏感的特性，而整个飞行控制的关键就是姿态控制，目前，相关的控制方法有模糊自整定PID控制[4]、鲁 棒控制[5]、粒子群优化神经网络控制[6]、无静差跟踪控制[7]、自适应神经模糊控制[8]、滑模控制[9]、输出反馈控制[10−11]等。本文作者针对纵列式双旋翼无人机姿态控制系统中欠驱动、多变量、强耦合的控制问题，设计串级线性自抗扰控制器，有效地解决了以上控制问题，并经过参数整定，得到良好的控制效果。

1 线性自抗扰控制器的基本原理

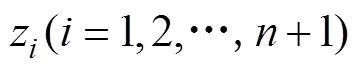
1.1 线性跟踪微分器(LTD)

设计跟踪微分器的目的是给系统输入安排过渡过程，得到光滑的输入信号，降低系统初始误差。

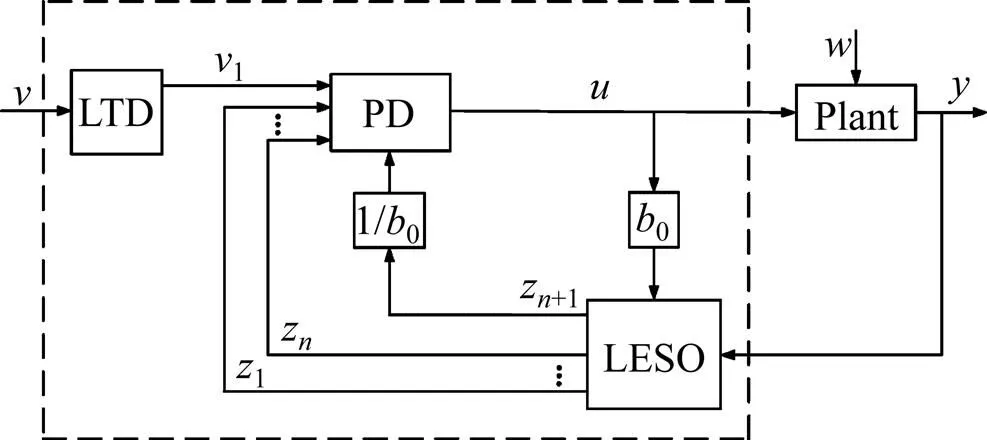
图1 线性自抗扰控制器

以二阶系统为例，连续形式的线性跟踪微分器算法为

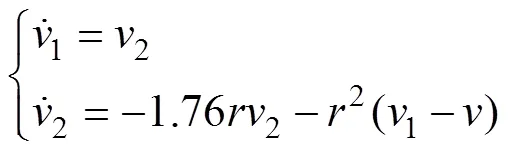
式中：为跟踪微分器的输入信号变量；1为的跟踪信号变量；2为输入的微分信号变量；为决定跟踪速度的参数。

1.2 线性扩张状态观测器(LESO)

扩张状态观测器除系统自身的状态外，还将系统模型自身的不确定性和系统外部扰动作为总扰动，扩张出另一个状态。通过观测器估算总扰动，并加到控制器中进行补偿，这样就能使原来的非线性控制系统变成线性的积分器串联控制系统。上述动态估计补偿总扰动的技术，便是自抗扰控制技术的最核心技术。

连续形式的线性扩张状态观测器算法为

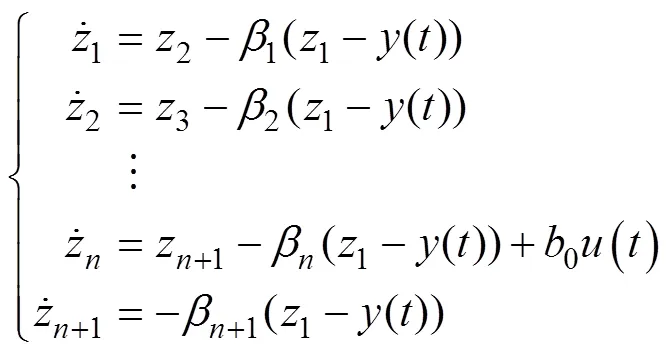
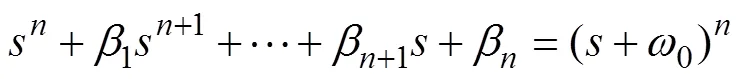
1.3 线性误差控制律

用LESO进行动态补偿之后，系统变成积分器串联控制系统，因此，只需采用较为简单的线性PD控制律就可以达到控制目的，线性误差控制律算法为

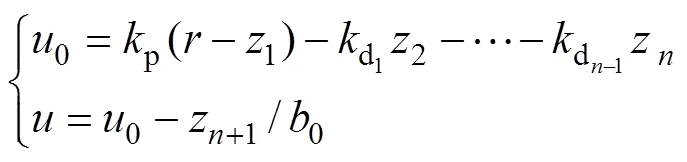
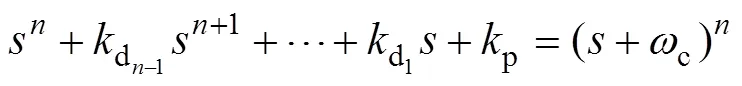
2 串级线性自抗扰控制器的设计

2.1 二阶n级串级线性自抗扰控制器的设计

设有个串联的二阶被控对象，即

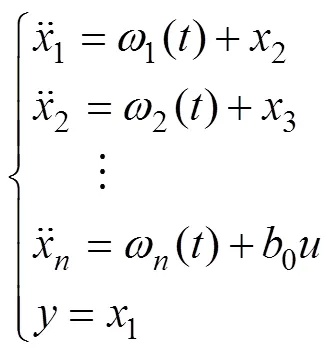
式中：，，…，为系统中的未知扰动，控制目的是让x1跟踪事先设定好的期望轨迹，让真实控制量u驱动xn，xn驱动xn−1，直到x2驱动x1达到控制目标为止。设x2为虚拟控制量u1，x3为虚拟控制量u2，以此类推，xn为虚拟控制量un−1，用自抗扰控制器来确定让x1跟踪目标v(t)的控制量u1，然后以u1为期望轨迹，对式(6)中第2式用自抗扰控制器来确定让状态x2跟踪u1的控制量u2，直到确定出真实控制量u为止。按照这个设计思想，二阶n级串级线性自抗扰控制器结构图如图2所示。

将式(6)展开，即

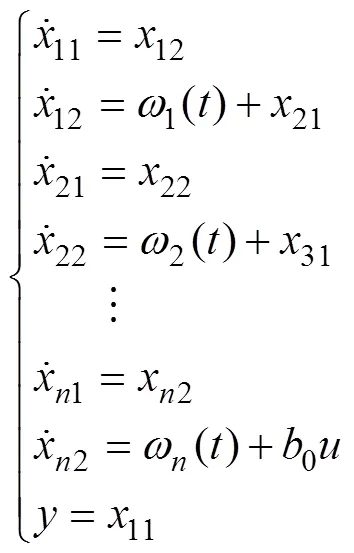
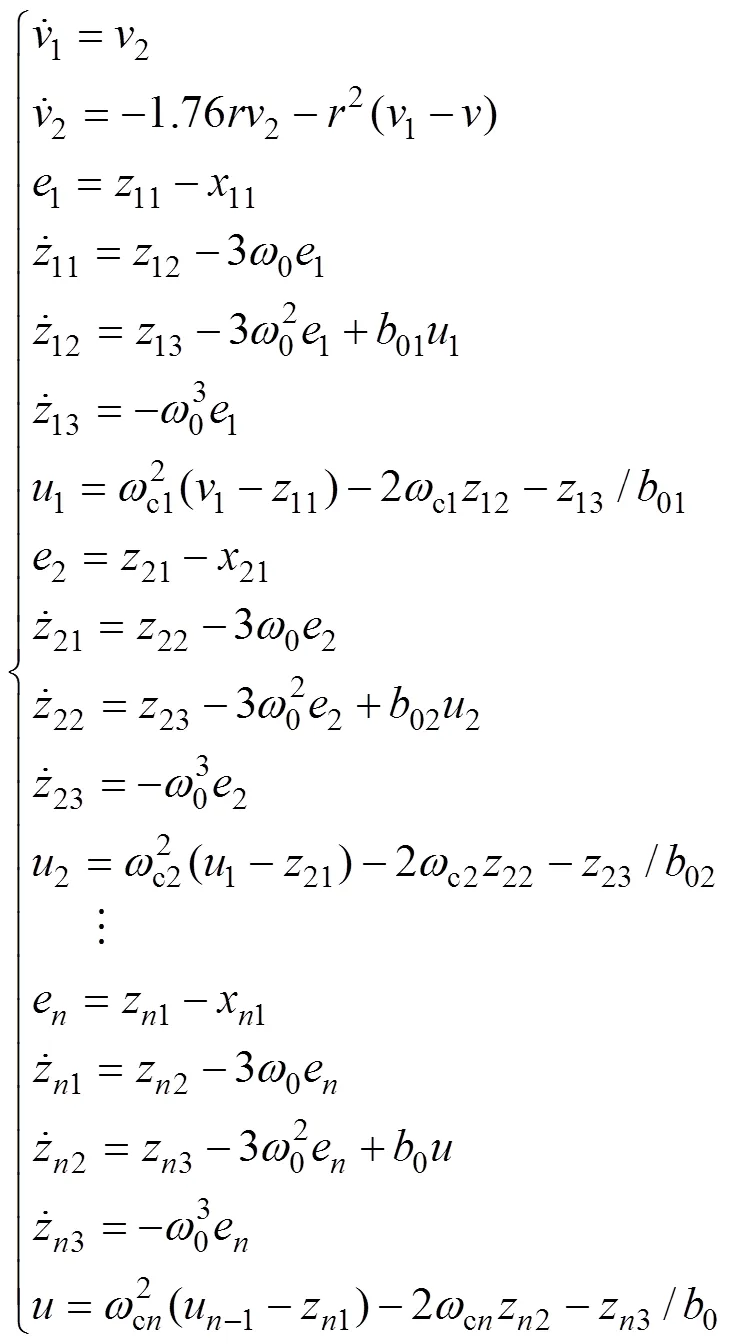
2.2 二阶2级串级线性自抗扰控制器的设计与仿真

设有2个串联的二阶被控对象如下式所示：

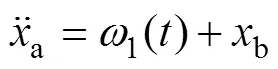
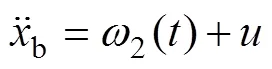
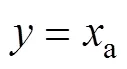
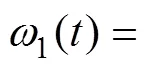
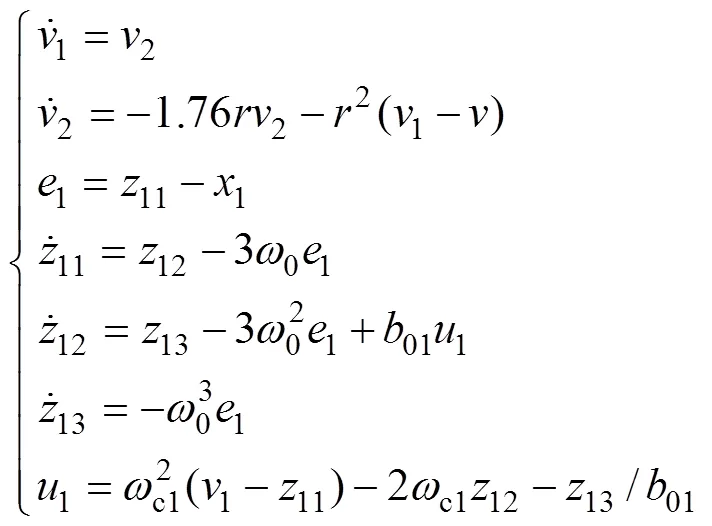
得到虚拟控制量1，以此作为3的期望轨迹。二阶LADRC2的控制算法为

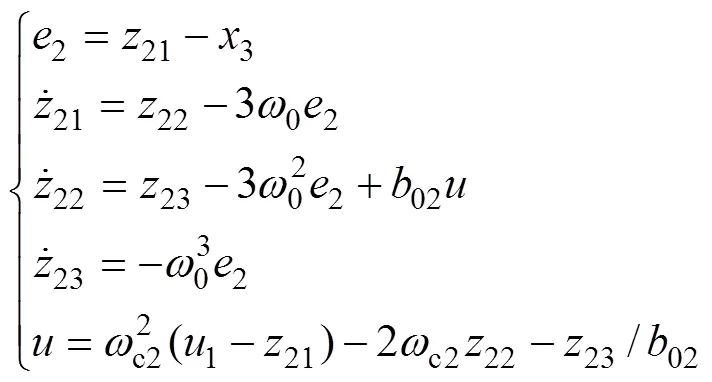
将二阶LADRC1和二阶LADRC2串联起来就是2个串联的二阶被控对象的串级自抗扰控制器，其结构图如图3所示。

3 串级LADRC在双旋翼无人机飞行姿态控制中的应用

3.1 纵列式双旋翼无人机姿态控制系统的模型

纵列式双旋翼无人机姿态控制系统[12−14]的结构示意图如图6所示。

纵列式双旋翼无人机姿态控制系统[14−16]的数学模型为

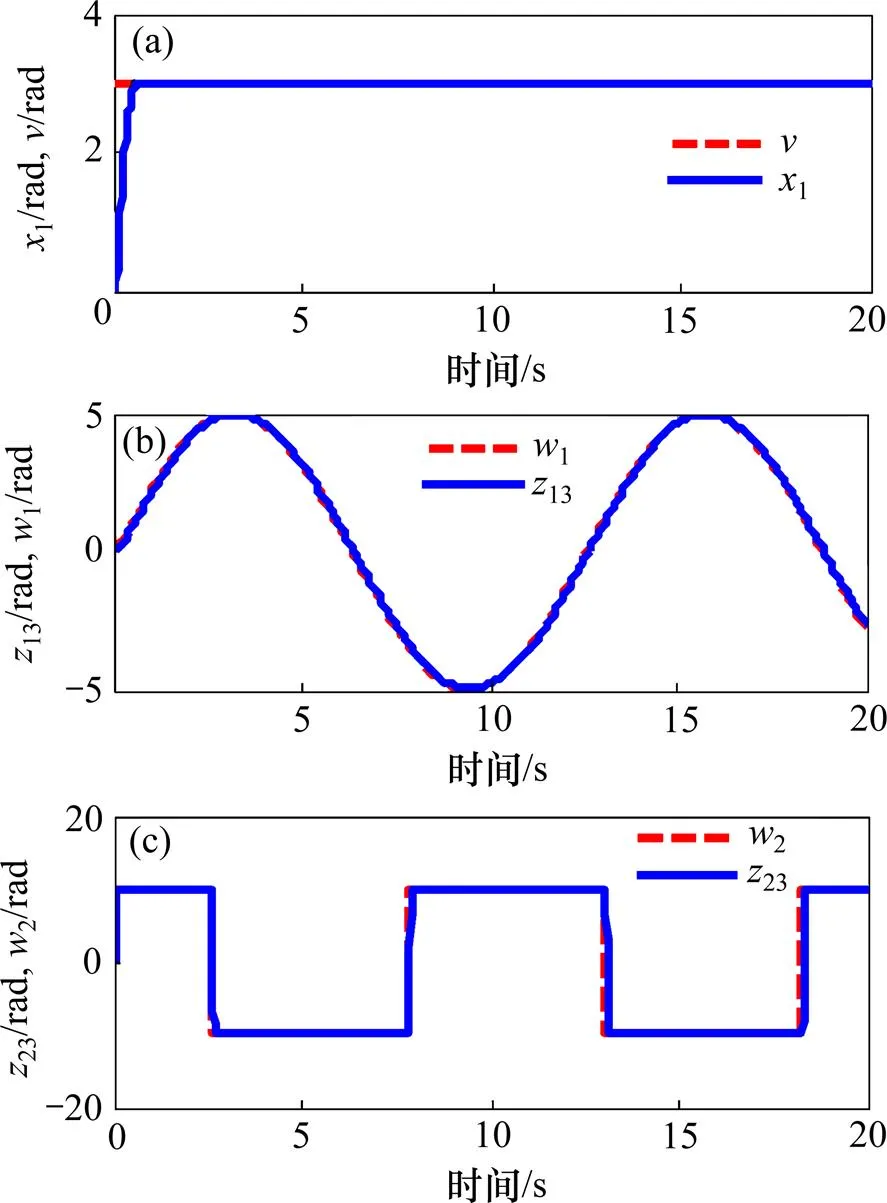
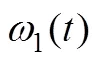
图4 LADRC仿真结果

Fig. 4 Simulation results of LADRC

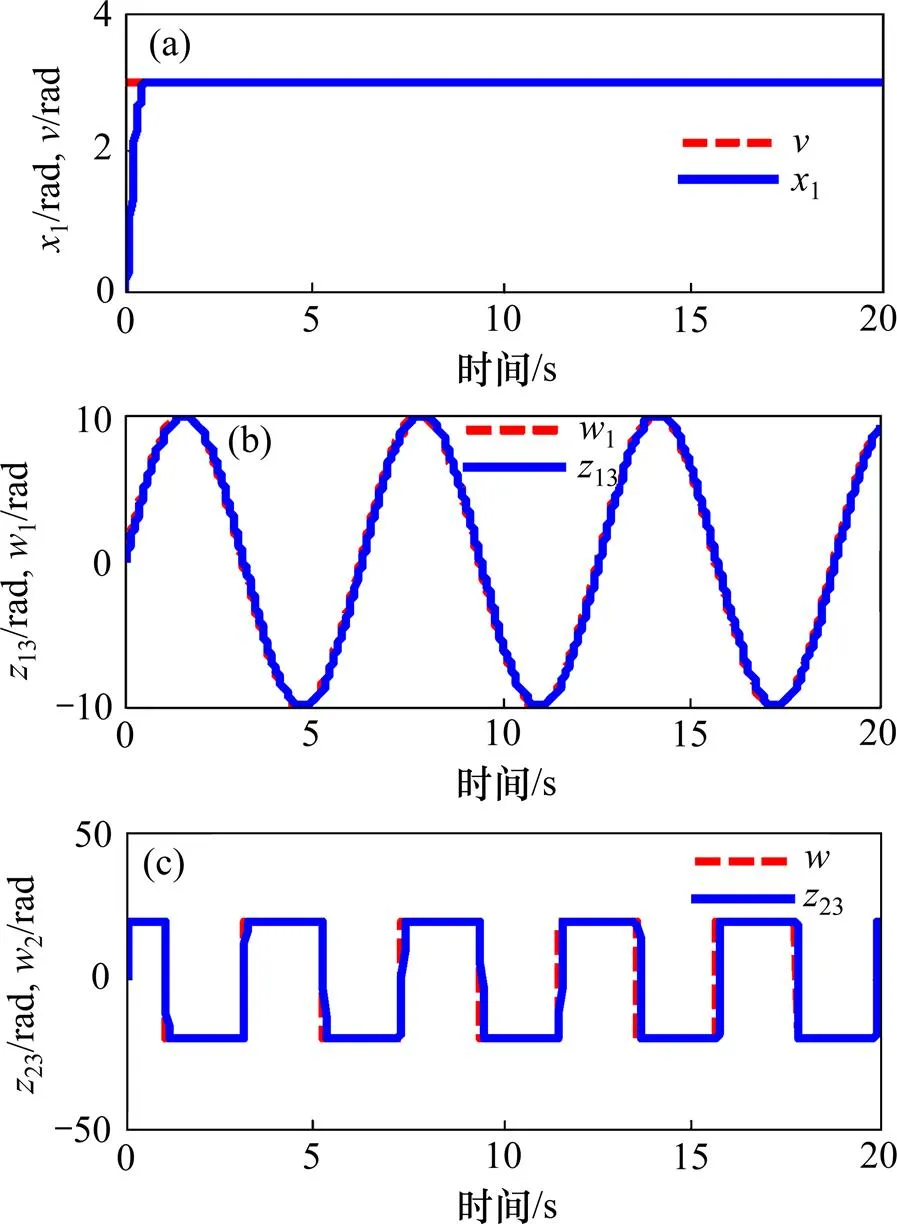
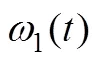
图5 二阶2级串级LADRC仿真结果

Fig. 5 Simulation results of second order second level cascade LADRC

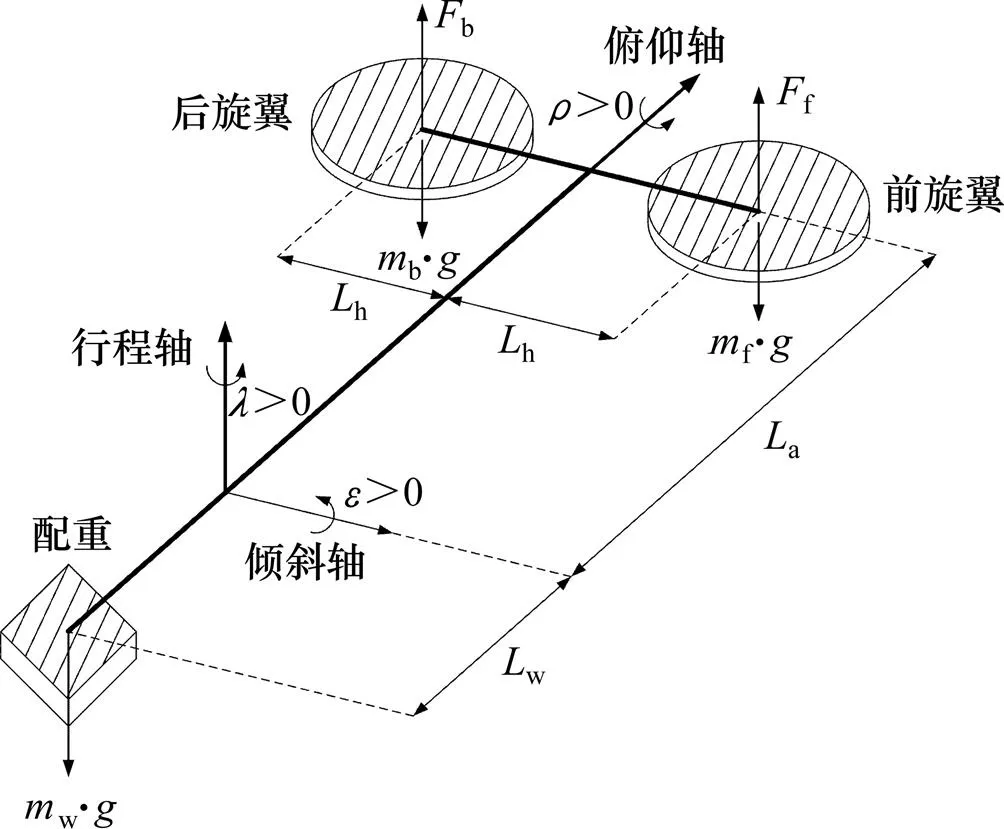
图6 纵列式双旋翼无人机姿态控制系统结构示意图

3.2 串级LADRC的设计

分析双旋翼无人机姿态控制模型可知，首先，要对模型进行解耦，设虚拟控制量1和2，双旋翼无人机模型改写成

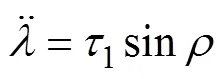
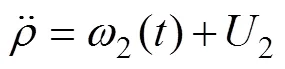
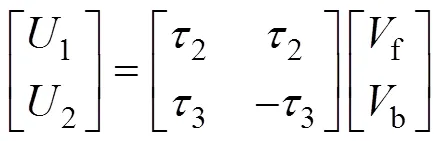
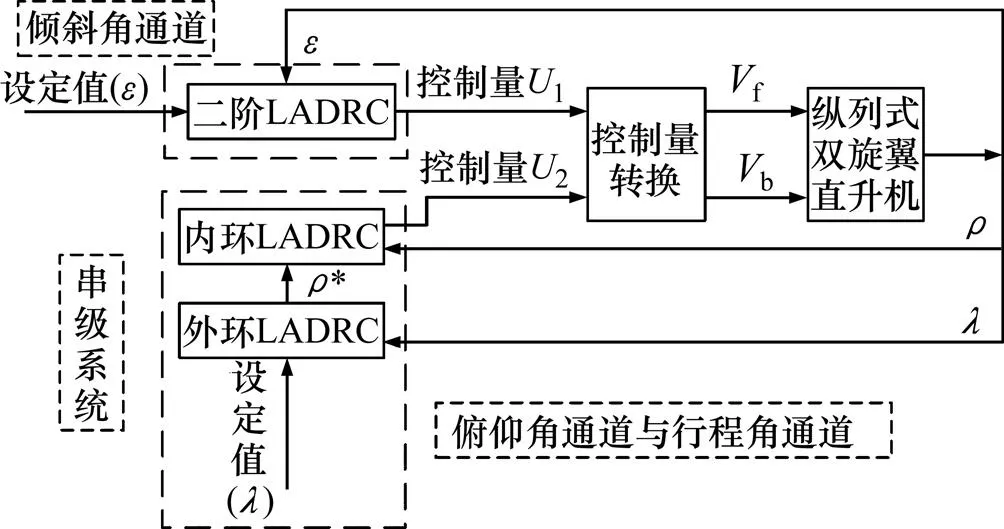
图7 双旋翼无人机姿态控制框图

倾斜角通道线性误差控制律算法如下：

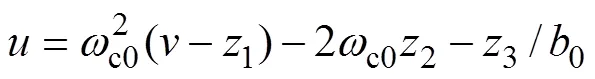
俯仰角通道和行程角通道的串级系统线性误差控制律算法如下：

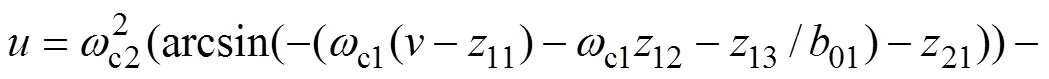
通过自抗扰控制器可以得到虚拟控制量1和2，然后通过控制量转换可以获得电机的真实控制输入量f和b，控制量转换如下：

4 纵列式双旋翼无人机飞行姿态控制仿真

根据前面所述的设计方法设计串级线性自抗扰控制器，并在MATLAB环境下进行无人机飞行姿态 仿真。

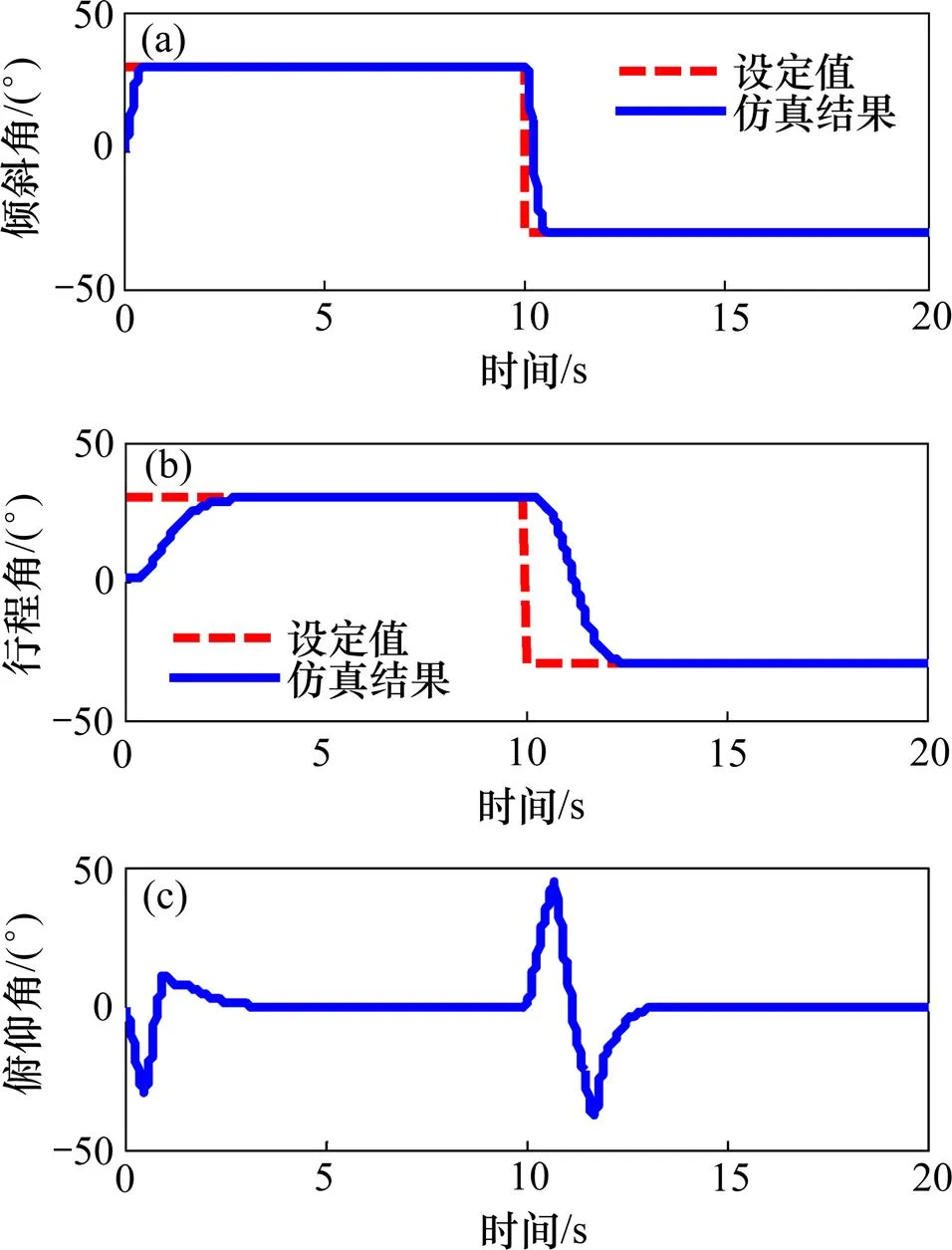
(a) 倾斜角；(b) 行程角；(c) 俯仰角

Fig, 8 Results of simulation (no disturbances)

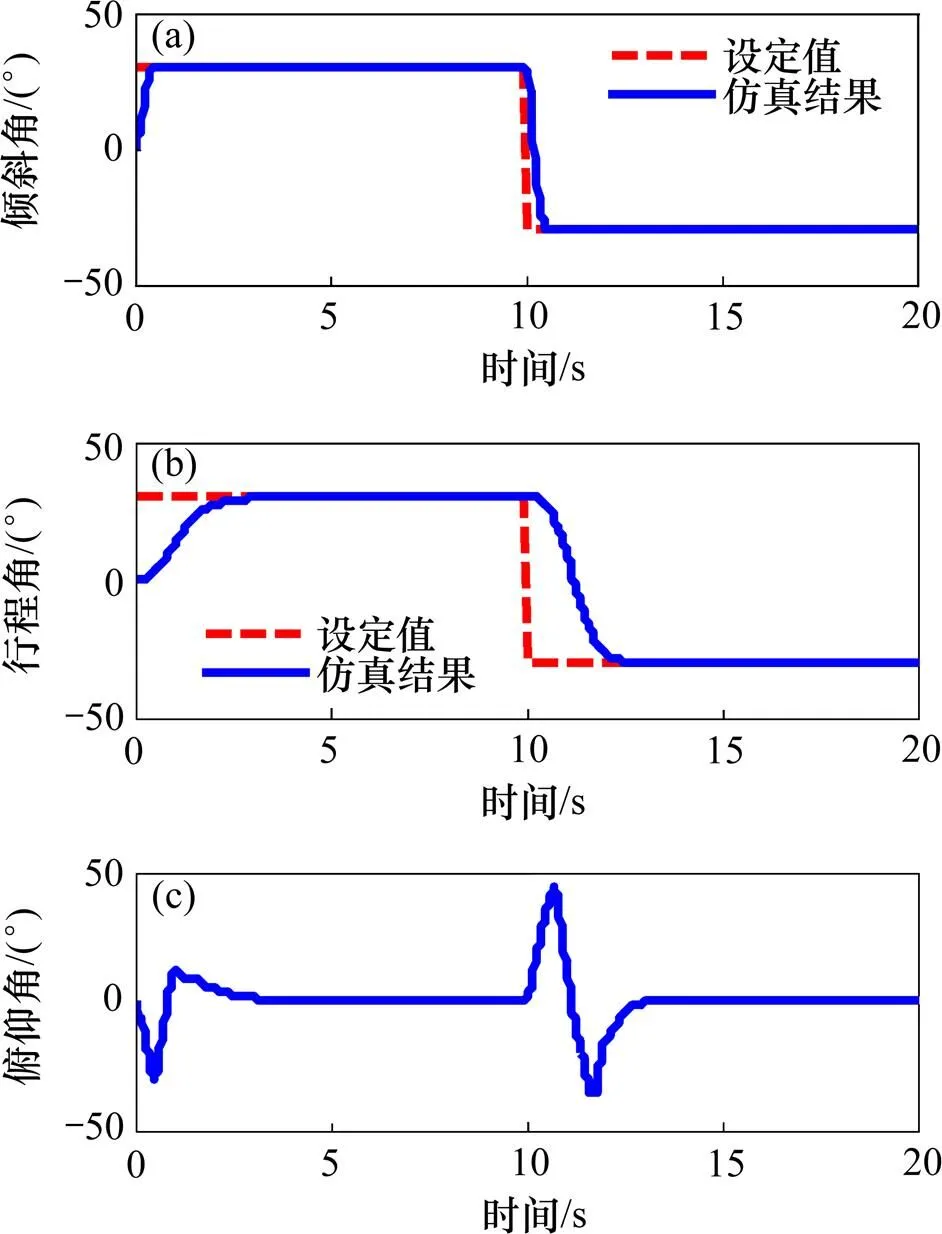
(a) 倾斜角；(b) 行程角；(c) 俯仰角

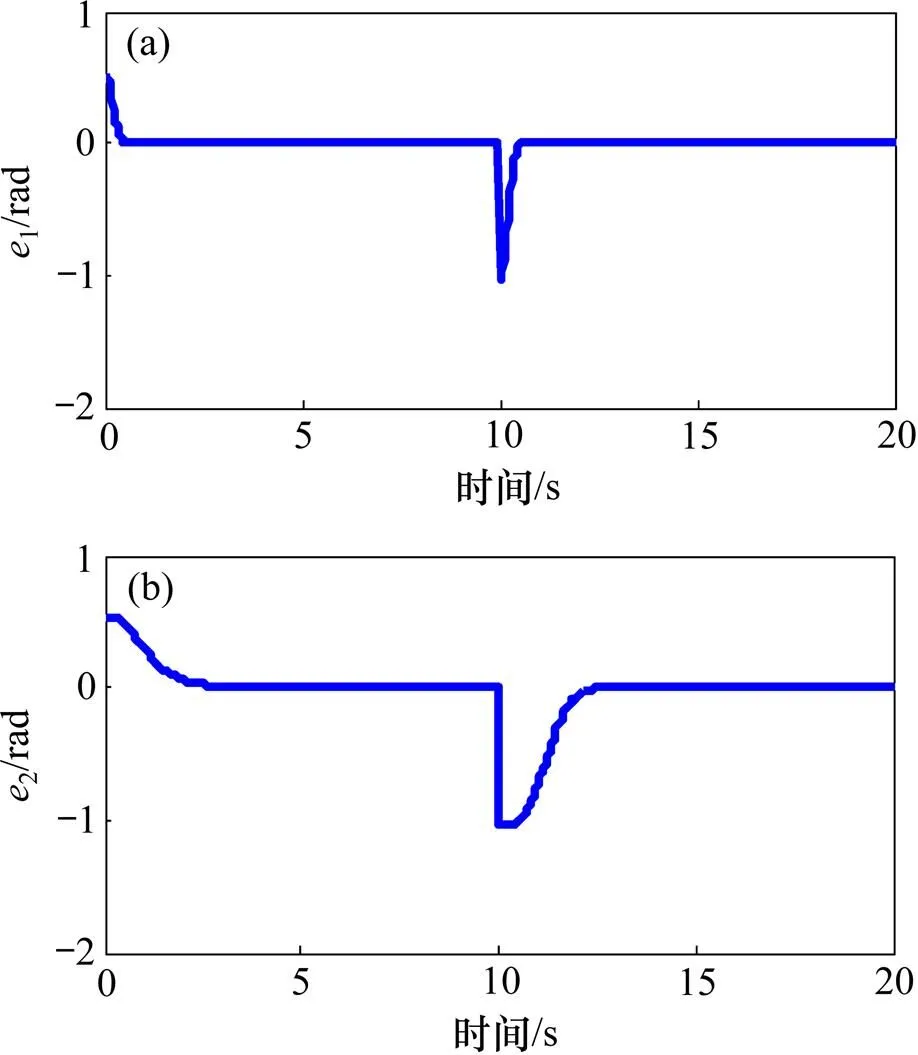
(a) 倾斜角的输入输出相对误差；(b) 行程角的输入输出相对误差

(a) 对扰动1的观测；(b) 对扰动2的观测

5 结论

1) 采用跟踪微分器可以得到准确的设定值微分信号，并且可以给系统输入安排过渡过程，得到光滑的输入信号，降低系统初始误差。

2) 采用扩张状态观测器可以获得系统总扰动的估计值，并将其补偿到控制器中，可消除扰动对系统的影响，提高系统的鲁棒性和抗干扰能力。

3) 采用虚拟控制量将系统改为串级控制，简化了控制器的设计过程。

4) 串级线性自抗扰控制器参数少、易整定、设计简单，能够解决双旋翼无人机姿态控制中非线性、强耦合以及对扰动敏感等控制问题，满足工程实际的需要，是一种非常有效的控制方法。

[1] HAN Jingqing. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900−906.

[2] GAO Zhiqing. Scaling and bandwidth-parameterization based controller tuning[C]// Proceedings of the 2003 American Control Conference. Denver. America: IEEE, 2003: 4989−4996.

[3] 张亚飞. 纵列式直升机飞行动力学建模及平衡、稳定性和操纵性计算[D]. 南京: 南京航空航天大学航空航天学院, 2009: 1−30. ZHANG Yafei. A mathematical model of tandem helicopter flight dynamics and calculating on the trim, stability and handling quality[D]. Nanjing: Nanjing University of Aeronautics and Astronautics. School of Aerospace Engineering, 2009: 1−30.

[4] 葛金来, 张承慧, 崔纳新. 模糊自整定PID控制在三自由度直升机实验系统中的应用[J]. 信息与控制, 2010, 39(3): 342−347. GENG Jinlai, ZHANG Chenghui, CUI Naxin. Fuzzy self-tuning PID controller in the 3-DOF helicopter experimental system[J]. Information and Control, 2010, 39(3): 342−347.

[5] 胡悦. 基于鲁棒控制的三自由度直升机半实物仿真实验[J]. 兵工自动化, 2016, 35(1): 72−74. HU Yue. Semi physical simulation experiment of three DOF helicopter based on robust control[J]. Ordnance Industry Automation, 2016, 35(1): 72−74.

[6] 王显博. 基于三自由度直升机模型的粒子群优化神经网络控制算法研究[D]. 哈尔滨: 哈尔滨理工大学自动化学院, 2016: 1−50. WANG Xianbo. Research on the particle swarm optimization neural net control based on three-DOF helicopter model[D]. Harbin: Harbin University of Science and Technology. School of Automation, 2016: 1−50.

[7] 岳新成, 杨莹, 耿志勇. 三自由度直升机模型的无静差跟踪控制[J]. 系统仿真学报, 2007, 19(18): 4279−4283. YUE Xincheng, YANG Ying, GENG Zhiyong. No steady-state error tracking control of 3-DOF experimental helicopter system[J]. Journal of System Simulation, 2007, 19(18): 4279−4283.

[8] 武俊峰, 贾婧媛. 三自由度直升机模型自适应神经模糊控制[J]. 哈尔滨理工大学学报, 2015, 20(2): 35−40. WU Junfeng, JIA Jingyuan. Research on adaptive neural fuzzy control of 3-DOF helicopter model[J]. Journal of Harbin University of Science and Technology, 2015, 20(2): 35−40.

[9] WITT J, BOONTO S, WERNER H. Proximate model predictive control of a 3-DOF helicopter[C]// Proceedings of the 46th IEEE Conference on Decision and Control. New Orleans, USA: IEEE, 2007: 4501−4506.

[10] KUTAY A T, CALISE A J, IDAN M. Experimental results on adaptive output feedback control using a laboratory model helicopter[J]. IEEE Transactions on Control Systems Technology, 2005, 13(2): 196−202.

[11] KIEFER T, KUGI A, GRAICHEN K. Feedforward and feedback tracking control of a 3DOF helicopter Experiment under input and output constrains[C]// Proceedings of the 45th IEEE Conference on Decision and Control. San Diego, USA: IEEE, 2006: 1586−1593.

[12] LIU Hao, LU Geng, ZHONG Yisheng. Robust LQR attitude control of a 3-DOF laboratory helicopter for aggressive maneuvers[J]. IEEE Transactions on Industrial Electronics, 2013, 60(10): 4627−4636.

[13] 胡春华, 朱纪洪, 孙增圻. 纵列式无人直升机建模及其精确线性化方法研究[J]. 控制与决策, 2004, 19(9): 1074−1077. HU Chunhua, ZHU Jihong, SUN Zenqi. Modeling and exact linearization for an unmanned tandem helicopter[J]. Control and Decision, 2004, 19(9): 1074−1077.

[14] 陈增强, 李毅, 袁著祉, 等. 串级自抗扰控制器在纵列式双旋翼直升机飞行姿态控制中的应用[J]. 控制理论与应用, 2015, 32(9): 1219−1225. CHEN Zengqiang, LI Yi, YUAN Zhuzhi, et al. Attitude control of tandem rotor helicopter based on cascade active disturbance rejection control[J]. Control Theory & Application, 2015, 32(9): 1219−1225.

[15] ZHU Bo, LIU Hongtao, LI Zhan. Robust distributed attitude synchronization of multiple three-DOF experimental helicopter[J]. Control Engineering Practice, 2015, 36(1): 87−99.

[16] 唐光辉, 侍洪波. 三自由度直升机模型鲁棒控制器设计[J]. 华东理工大学学报(自然科学版), 2010, 36(5): 105−111. TANG Guanghui, SHI Hongbo. Robust controller design for 3-DOF helicopter model[J]. Journal of East China University of Science and Technology(Natural Science Edition), 2010, 36(5): 105−111.

[17] WANG Xiuyan, ZHAO Changli, LI Zongshuai. Robust H-infinity tracking control of 3-DOF helicopter model[C]// Proceedings of 2010 International Conference on Measuring Technology and Mechatronics Automation. Changsha, China: IEEE, 2010: 279−282.

[18] GAO Weinan, FANG Zheng. Adaptive integral backstepping control for a 3-DOF helicopter[C]// Proceedings of 2012 IEEE International Conference on Information and Automation. Shenyang, China: IEEE, 2012: 190−195.

[19] 郑博, 钟宜生. 一类Quanser直升机的鲁棒姿态调节器设计[J]. 清华大学学报(自然科学版), 2011, 51(3): 323−327. ZHENG Bo, ZHONG Yisheng. Robust attitude regulator design for a class of Quanser helicopter[J]. Journal of Tsinghua University(Natural Science Edition), 2011, 51(3): 323−327.

[20] BORIS A, DIMITRI P, ALEXANDER L. Adaptive control of 3-DOF motion for LAAS helicopter benchmark: design and experiments[C]// Proceedings of the 2007 American Control Conference. New York, USA: IEEE, 2007: 3312−3317.

Attitude control of tandem rotor UAV based on cascade linear active disturbance rejection control

ZHANG Yong1, CHEN Zengqiang1, ZHANG Xinghui2, SUN Qinglin1, SUN Mingwei1

(1. School of Computer and Control Engineering, Nankai University, Tianjin 300350, China;2. Tianjin Sino-German University of Applied Sciences, Tianjin 300350, China)

The structures of the linear active disturbance rejection controller(LADRC) and cascade linear active disturbance rejection controller were described in detail, including linear tracking differentiator, linear extended state observer and linear error control law. And the typical algorithms of the each part were given as well. In order to solve the control problems of under-actuated, multivariable and strong coupling in tandem rotor UAV attitude control system, the cascade linear active disturbance rejection controller was designed. The results show that the cascade LADRC has fewer parameters and is convenient for parameter setting, it can meet the requirement of control accuracy and rapidity, and it also has strong robustness, anti-disturbance ability and decoupling ability.

linear active disturbance rejection controller(LADRC); cascade control; linear extended state observer; tandem rotor UAV; attitude control

TP273

A

1672−7207(2019)03−0564−08

10.11817/j.issn.1672-7207.2019.03.009

2018−04−25；

2018−06−17

国家自然科学基金资助项目(61573197，61573199) (Projects(61573197, 61573199) supported by the National Natural Science Foundation of China)

陈增强，教授，博士生导师，从事智能预测控制、自抗扰控制研究；E-mail: Chenzq@nankai.edu.cn

(编辑 刘锦伟)