基于应力强度因子的发动机连杆裂解力数值模拟分析

党林媛，卢耀辉，卢川，朱生长，毕伟

（西南交通大学 机械工程学院，成都 610031）

以往的连杆生产工艺复杂，并且废品率高。在这种情况下，一种新的连杆特种加工工艺——连杆裂解工艺被提出来。这种连杆加工方法能够降低生产成本，保证连杆的装配质量[1-3]。连杆裂解工艺是基于断裂力学提出的，该工艺在连杆的大头内侧预制裂解槽及初始微裂纹，使裂纹尖端产生应力集中；之后对连杆大头孔内侧施加垂直于断裂面的载荷，当载荷大于临界值时，连杆将发生裂解[4-7]。裂解力过小，则连杆无法实现裂解，且会对设备产生损害；裂解力过大，会使加工后的大头孔失圆，影响杆部与盖部装配精度，并且还会引入较大的残余应力。残余应力的释放会影响装配后大头孔尺寸精度和形状的稳定性，进而影响发动机工作性能。由此可见，合理确定裂解力的阈值，对于实际生产具有重要的指导意义[8-9]。

连杆裂解工艺的基本原理是主动利用裂纹扩展，通过预制裂解槽，并施加合适的裂解力来控制连杆大头启裂位置和裂纹扩展路径。因此，连杆裂解工艺的进步与裂纹扩展的深入研究关系密切[10]。对弹性体进行裂纹扩展模拟时，普遍以应力强度因子是否高于临界值来判断裂纹是否扩展。目前广泛用于分析裂尖应力强度因子的方法主要分为理论解法及数值法。结构复杂且裂纹形式多样时，理论求解应力强度因子存在一定难度。另外，传统的数值方法是基于连续介质理论进行分析计算的，即认为单元内部连续完整，要求单元内部位移场连续。这种情况下，控制裂尖网格质量十分困难，导致应力强度因子计算可能存在较大误差。基于传统有限元法提出的扩展有限元法（XFEM）[11]在原有单元位移函数中增加了跳跃函数及裂尖增强函数[12-14]。裂纹可存在于单元内部，从而简化有限元建模。仿真裂纹扩展时，根据数值计算结果，从最危险点处启裂。与传统方法相比，可更精准地模拟连杆裂解情况。张开型裂纹所需的外力低，容易发生低应力脆性断裂，连杆裂解即按照此裂纹类型制造敏感应力场，因此理想状态下连杆裂解属于Ⅰ型断裂。文中依据断裂力学中的张开型断裂模式，在完成切口预制的基础上，预制了初始微裂纹，应用XFEM对连杆裂解工艺过程中的裂解力进行数值模拟，为连杆裂解中裂解力阈值的确定提供有效参考。

1 连杆裂解工艺数值模拟方法

1.1 裂解加工原理

在进行裂解加工前，首先需要加工出整体连杆，之后在大头孔内连杆盖与连杆体接触面处加工出裂解槽，并预制初始微裂纹。这种情况下，在连杆大头孔处作用垂直于连杆盖与连杆体接触面的载荷时，会在预制微裂纹尖端产生应力集中。由断裂力学理论可知，当裂尖应力强度因子达到材料断裂韧度时，连杆大头将沿预制裂解槽开裂，实现连杆裂解，如图1所示。裂解后的连杆盖与连杆体接触面呈犬牙交错态，每个连杆体仅有一个连杆盖与之完美配合，配合精度极高。

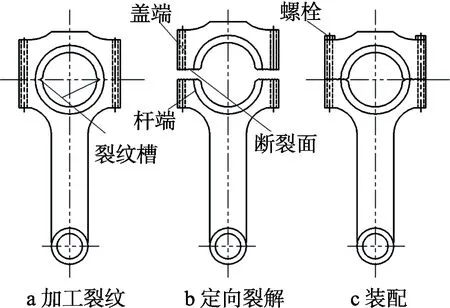
图1 连杆裂解加工原理

1.2 XFEM基本理论

有限元模型划分好单元后，定义一条分界线或一个分界面，将其视为裂纹（如图 2所示）。根据断裂力学和有限元法知识可知，裂纹所在单元内位移场不连续，并且单元内裂尖存在应力集中现象。为描述单元内及裂尖位移场的不连续性及奇异性，Belytschko基于原有单元位移函数，提出了跳跃函数和裂尖增强函数：

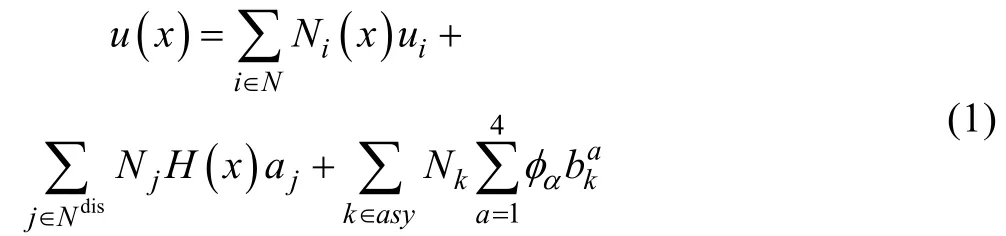
式中：i为所有节点的集合；j为不包含裂尖单元的节点（图中“圆圈”）；k为包含裂尖单元的节点（图中“正方形”）；Ni,Nj,Nk为节点形函数；ui,aj, bαk为节点位移；H（x）为跳跃函数。描述单元内不连续位移场，见式（2）：

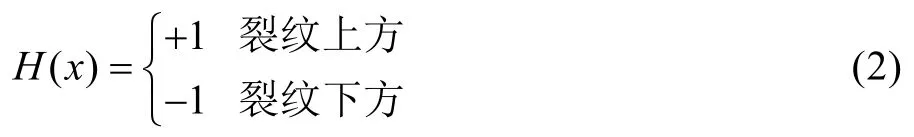
φα（x）为裂尖增强函数，描述裂尖附近的奇异位移场，用极坐标表示（其中，r,θ所在坐标系的坐标原点为裂尖）：

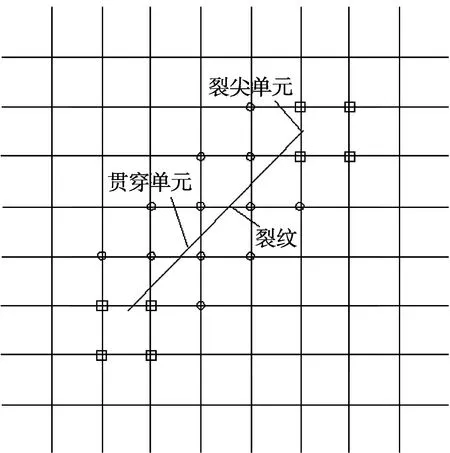
图2 位于网格内任意位置的裂纹

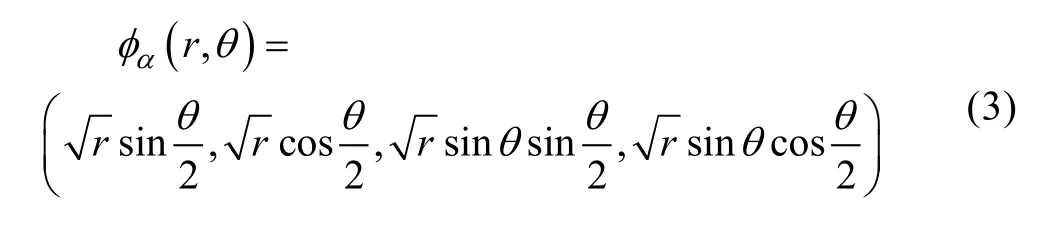
1.3 有限元模型的建立

连杆材料为高碳合金钢C70S6，其裂解槽几何参数和材料参数见表1。在裂解过程中，连杆小头端、杆身几乎不产生变形和位移，在有限元分析过程中可以忽略。由于直切口连杆关于主轴中心对称，因此建立大头端的1/2模型进行分析。结构圆角对连杆裂解过程几乎不产生影响，因此在建模中简化。通过静力分析求解裂解力及裂解力的影响因素，因此未考虑加载时的动态冲击。分析过程中，载荷直接通过多点约束（MPC，Multi-points constraint）施加在连杆盖上[15]。

表1 裂解槽几何特征参数

定义分析选项时，采用几何非线性计算裂纹扩展速率和路径。计算应力强度因子时，设定裂纹不扩展，应不考虑几何非线性。设置裂纹类型为XFEM裂纹，计算裂纹扩展速率及路径时可扩展，计算应力强度因子时不可扩展。

连杆断裂剖分时，由于微裂纹于切口根部萌生，同时发生小范围屈服，为精确分析塑性区范围，需细化切口附近网格。根据上述特点，将连杆大头端划分为裂纹区与非裂纹区，连杆模型区域划分情况如图3所示。预制初始裂纹附近区域网格采用8节点六面体单元C3D8R，有限元模型单元总数约为56万，裂纹附近区域网格数大于45万，占总网格的数80%以上。

根据实际情况确定其边界条件和约束。在相互作用模块创建耦合约束，在耦合点加载集中作用力，集中作用力垂直于预定断裂面加载，对称面上施加对称约束。连杆裂解时，连杆小头固定，连杆大头在动套的作用下使连杆盖与连杆体沿预制裂解槽裂解分离，因此在大头截断处施加位移约束，如图4所示。采用静力分析裂纹区域的应力强度因子，并与材料断裂韧度进行对比，通过反复试算最终得到材料断裂韧度对应的裂解力。

图3 连杆模型网格划分情况

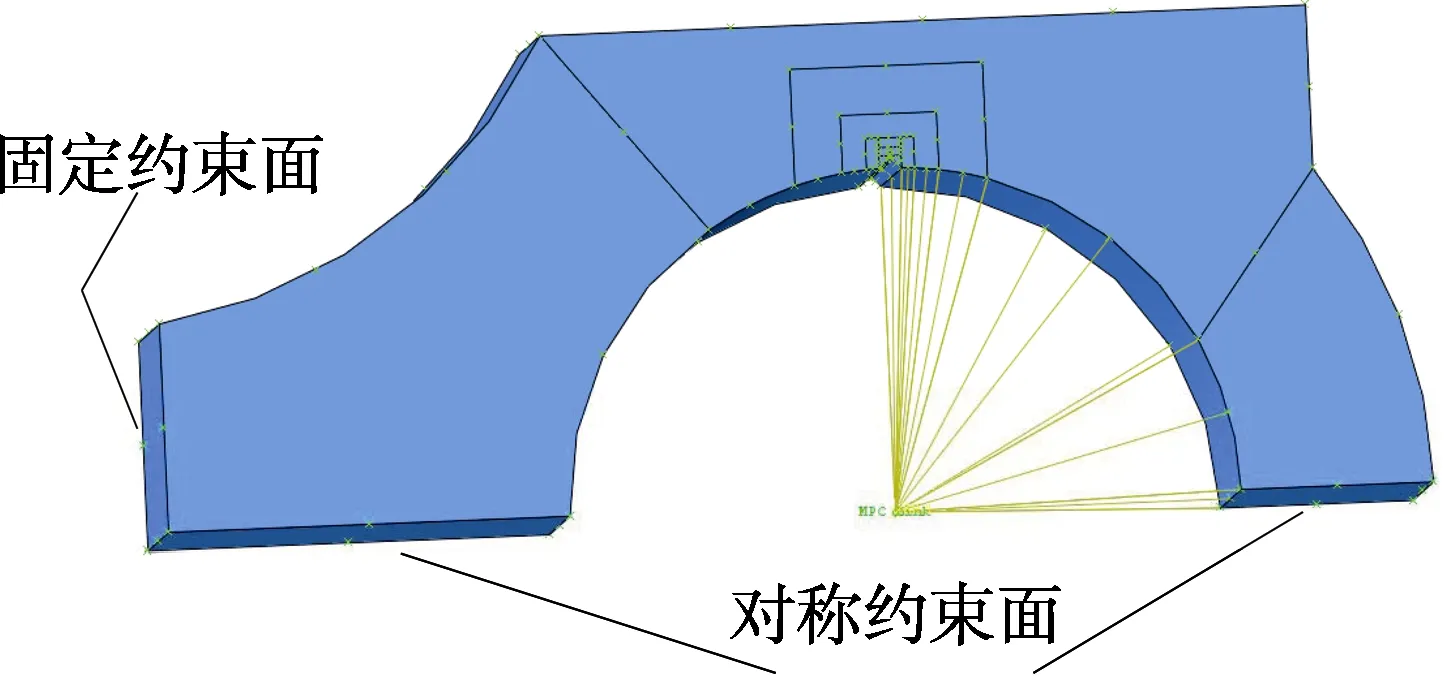
图4 载荷及边界条件定义

2 计算结果及分析

2.1 初始微裂纹长度与连杆裂解力的关系

断裂力学中，应力强度因子KI用于描述外力和裂纹尺寸的几何效应，可概括为：

式中：a代表裂纹特征尺寸；σ代表外力场；Y为几何形状因子，描述裂纹及结构几何的作用。

KI存在阈值KIC，KIC为断裂韧度。一定条件下，KIC为关于材料的常数，可由试验测定，KIC给出了材料抵抗裂纹扩展的抗力数据。在裂解过程中，连杆预定断裂面上的工作应力未达到连杆材料屈服应力的1/2，连杆整体绝大部分都处于弹性状态。只有在裂解槽根部存在半径远小于连杆及裂解槽尺寸的裂尖塑性区，并且周围都被广阔的弹性变形所包围。因此连杆裂解起裂可采用线弹性断裂判据[16]，即：

当结构的KI达到连杆结构所采用材料的断裂韧度KIC时，预制的初始裂纹发生失稳扩展，此时即使外力不再增加，裂纹也会迅速扩展直至断裂。文中对连杆裂解工艺的研究正是基于这一准则展开的。裂尖应力强度因子达到材料断裂韧度对应的载荷即为连杆裂解工艺所需的裂解力，该型连杆材料 C70S6的断裂韧度为39.74 MPa·m1/2。由于有限元模型建模时长度单位为mm，因此得到以MPa·mm1/2为单位的断裂韧度，即 1256.7 MPa·mm1/2。通过不断试算使K1=1256.7 MPa·mm1/2，进而得到对应的裂解力。该研究设置了不同长度初始微裂纹下的连杆裂解模型，对模型施加载荷，通过 XFEM 求解得到各裂纹长度下的裂解力，拟合得到初始裂纹长度与达到断裂韧度对应的连杆裂解力之间的关系如图5所示。

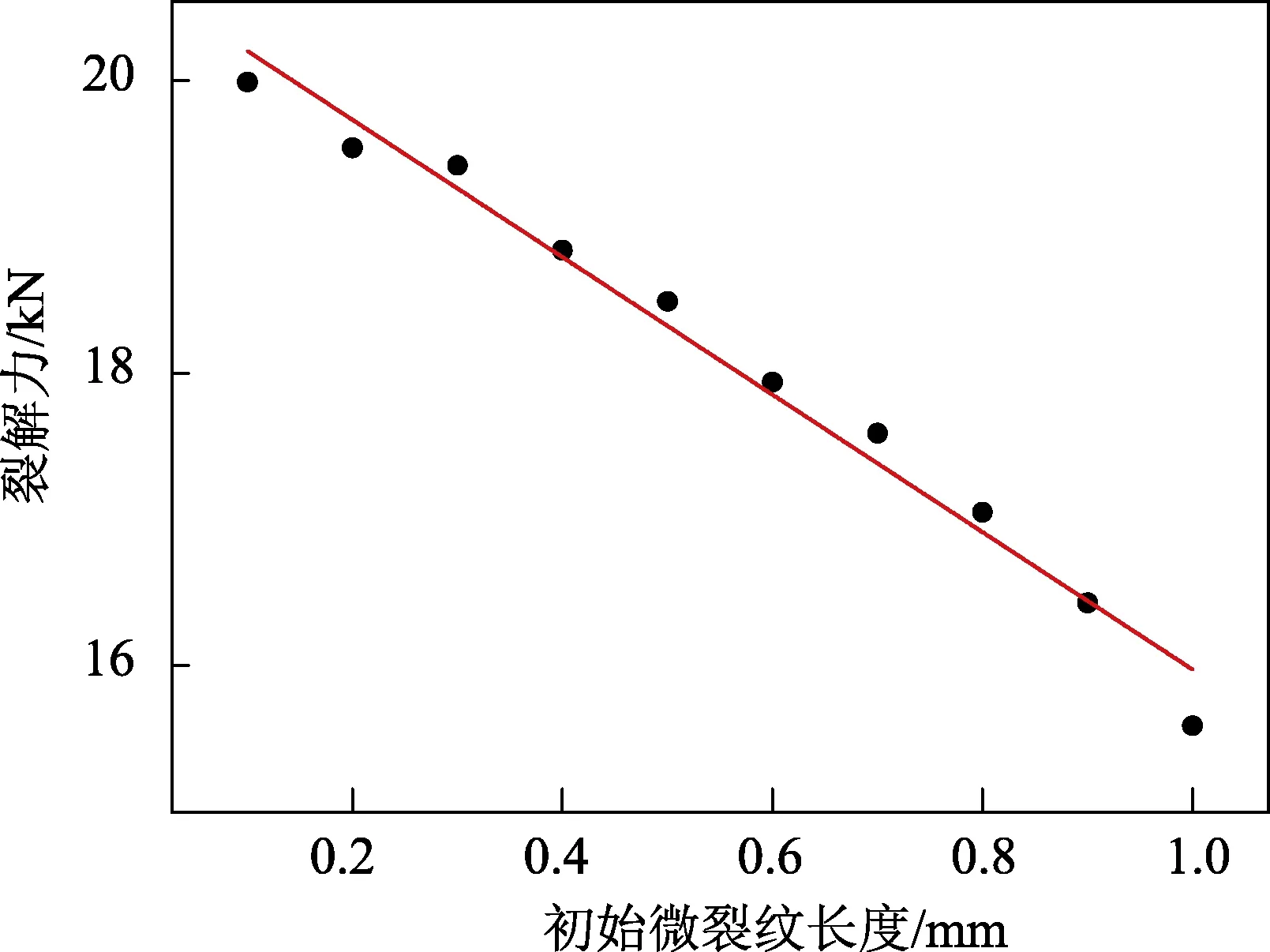
图5 连杆裂解力随初始微裂纹尺寸变化曲线

拟合优度R2=0.978 58。分析图5可以看出，预制的初始微裂纹长度与断裂韧度对应的裂解力两者之间呈线性负相关，且影响较明显。预制初始微裂纹尺寸为0.1 mm时，裂尖应力强度因子达到断裂韧度对应的裂解力20 kN；将预制的初始微裂纹长度增加到1 mm后，该值减小至15.6 kN，减小了28%。根据断裂力学知识和有限元理论可以得出，随着初始微裂纹长度的加大，连杆发生裂解所需的裂解力不断减小。加工完成后，要将连杆盖与连杆体进行配合。预制的初始微裂纹长度越长，配合时的接触面积必然越小，并且会增加加工工艺难度，影响加工精度和质量。由此可得，当裂解力能满足需要时，预制微裂纹长度应选取较小值。

2.2 裂解力对塑性区的影响

根据裂解工艺原理可以看出，裂解槽微裂纹尖端塑性区的存在，导致裂解过程中结构必然产生塑性变形。因此，裂纹尖端塑性区的大小直接决定了裂解完成后连杆盖与连杆体的啮合质量。裂纹尖端塑性区过大，会导致连杆盖与连杆体啮合质量较差，甚至导致连杆大头失圆，大幅增加连杆裂解工艺的次品率。连杆裂解力大小对裂尖塑性区的影响研究具有十分关键的工程意义。文中以初始微裂纹长度a=0.5 mm为例，其断裂韧度下的裂解力为18.49 kN。由于低于断裂韧度对应的裂解力不会是使裂纹扩展[4]，因此此处仅分析裂解力大于等于断裂韧度对应的裂解力对塑性区的影响，从而为裂解力阈值的合理确定提供指导。

不同裂解力下的塑性区如图6所示，在ABAQUS中进行相关设置，只显示超过屈服极限585 MPa的应力，低于屈服极限的以灰色显示。从模拟结果可以看出，裂纹尖端有着非常明显的应力集中，在预制的初始裂纹尖端处应力达到最大值，试样处于屈服阶段。由于裂纹面是自由边，应力值最小。同时可以看出，当裂解力增大时，塑性区明显增大，并且增长方向不是沿裂纹扩展方向，而是呈蝶形向两端扩展，与平面应变塑性区形状一致。通过与断裂力学理论对比，验证了裂尖应力场分析的正确性。当裂解力过大，达到30 kN时，连杆大头部分区域产生了严重的塑性变形，过大的塑性变形通常会导致连杆大头孔失圆，将严重影响连杆二次合装（安装到发动机）工艺。显而易见，塑性变形越小，越能改善大头孔失圆问题，并利于连杆断裂面啮合、装配及使用。当裂解力为 18.49 kN时，不仅可满足连杆裂解要求，并且裂纹尖端塑性区较小，能有效改善大头孔失圆问题，因此最为理想的裂解力为材料断裂韧度对应的裂解力。

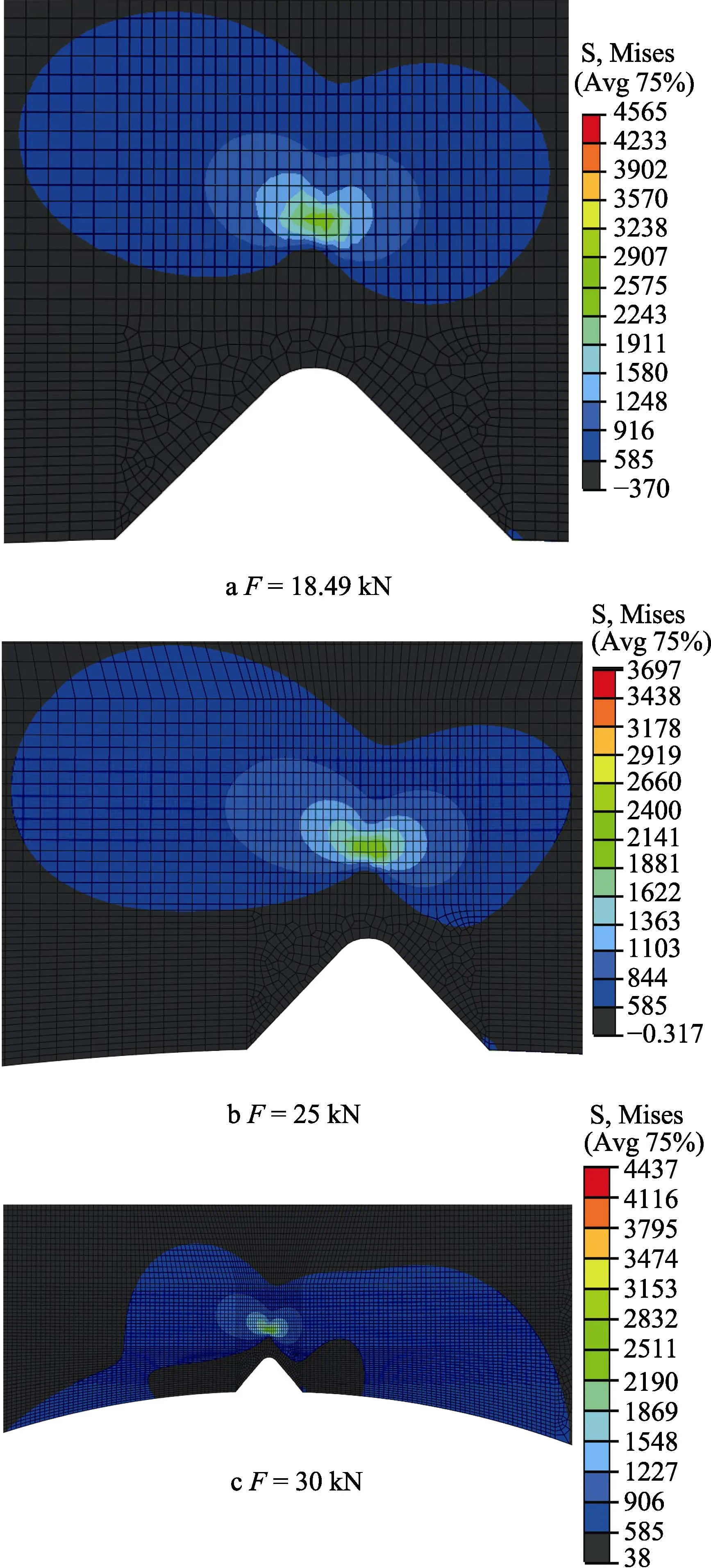
图6 不同裂解力下的塑性区

3 结论

1）基于XFEM理论建立了含不同长度初始微裂纹的连杆裂解有限元模型，以，裂纹便开始扩展为依据，通过不断试算得出应力强度因子达到临界值时的裂解力。通过大量计算和数据拟合得出初始微裂纹长度与裂解力之间的关系，从而得出裂解力和预制的微裂纹长度近似成负相关。

2）根据图5所示初始微裂纹长度与裂解力的拟合关系可以看出，为降低连杆裂解力，在工艺条件允许的情况下，预制的初始微裂纹长度尽量选取较大值。随着预制初始微裂纹长度的增加，必然造成加工余量增加，这就必然会减小连杆盖与连杆体间配合时的接触面积，同时提高了预制裂纹的难度。因此，当连杆裂解力能够满足需要时，初始微裂纹长度应取较小值。

3）当裂解时的实际裂解力小于材料断裂韧度对应的连杆裂解力时，会产生无法裂解的情况。当裂解的实际裂解力过大时，则会使预制微裂纹尖端的塑性区急剧扩大，导致大头孔失圆，致使裂解完成后的连杆盖与连杆体无法装配。在断裂韧度对应的裂解力下，不仅塑性区较小，也更接近平面应变状态，因此最为理想的裂解力为材料断裂韧度对应的裂解力。