基于仿水循环算法的梯级水库群多目标优化调度研究

吴智丁

(大唐水电科学技术研究院有限公司，广西 南宁 530025)

1 研究背景

我国水利资源丰富，如何综合考虑灌溉、发电、防洪和供水等需求是梯级水库群优化调度的核心问题，关系着社会、经济和环境等多方面的综合利益[1，2]。然而梯级水库群之间存在着水文、水力、电力、经济之间的强耦合关系，呈现多目标、非线性、变量多和约束强等特性[3-6]。传统优化方法，如线性规划、非线性规划和动态规划等，会面临难以直接求解、无法保证全局最优及维数灾等难题[7-11]，智能种群优化方法，如遗传算法(Genetic Algorithm，GA)、粒子群算法(Particle Swarm Optimization，PSO)、蛛群算法和布谷鸟算法等，又存在收敛速度慢、收敛早熟和鲁棒性差等问题[12-15]。因此，在梯级水库群优化调度中尝试引入新的优化算法，以实现收敛性能和计算速度的均衡仍然是学术界研究的热点和难点。

仿水循环算法(Water Cycle-like Algorithm，WCA)是近些年来出现的一种新的智能种群优化算法[16-18]，它模拟大自然水循环及水流动的过程，利用相对重力机制令水滴粒子在解空间内搜寻目标函数的最优解。同时构建汇流、分流、渗流、蒸发降雨4个优化策略，其中：①汇流策略使多个邻近水滴粒子汇聚为单个水滴，汇流后的水滴粒子质量变大，能有效提高搜索速度，令水滴迅速逼近最优解；②分流策略能防止单个水滴粒子质量过大而导致的收敛早熟，当水滴粒子大于限制值时，则分流为多个小水滴继续进行搜索；③渗流策略判断当水滴粒子相对重力较弱时分裂为多个细小水滴在当前位置周围进行局部搜索，大幅提高算法寻优能力；④蒸发降雨策略令相对重力为零，即迭代停滞的早熟水滴粒子蒸发并脱离当前位置，之后随机降雨至解空间内，令其重新参与搜索，有效解决水滴粒子早熟及陷入局部最优解的难题。基于以上迭代机制和搜索策略，使得WCA能按照当前的搜索情况自主改变水滴种群数量和水滴粒子质量，智能调配搜索资源，令算法自适应当前的计算需求。因此WCA真正实现了种群的智能化，搜索能力强、鲁棒性高，已经被广泛用于多个领域，成为近些年来智能种群算法的一个新亮点，然而目前这一算法尚未引入多目标水库群优化调度中。

本文对仿水循环算法进行研究，基于Pareto存档进化策略(Pareto Archived Evolution Scheme，PAES)，构建多目标寻优问题下的WCA改进重力迭代机制，提出多目标仿水循环算法(Multi-objective Water Cycle-like Algorithm，MWCA)，并将其应用于梯级水库群多目标优化调度中。

2 梯级水库群多目标优化调度数学模型

2.1 目标函数

梯级水库群兼具发电任务及民生、航运、农业、工业等供水用途，因此其调度策略的制定应兼顾这两方面的需求。本文构建梯级水库站群发电量最大及供水量最大的多目标优化调度模型，即在综合考虑各约束条件及给定调度期内各时段区间来水的情况下，尽可能最大化发电量以提高供电效益，同时最大化供水量以提升供水效益。

(1)发电量最大。在给定有限来水下应最大化出力，多承担电网负荷，提高调度时段内发电量，达到减少火电出力和节能减排的目的。

(1)

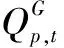
(2)供水量最大。供水量由农业灌溉供水量和工业、市政供水量组成，其中农业供水量主要来自河道区间引水，工业及市政供水量取自水库库区。提高流域及水库群的整体供水量，有利于本调度期内梯级水库群的供水效益和水能综合利用。

(2)

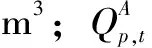
2.2 约束条件

(1)水量平衡约束。梯级水库群间相互联系紧密，上游水电站的出库流量、弃水量，区间来水量、农业灌溉供水量，本级水电站的发电流量、市政供水量、弃水量等都对本级水电站的库容和下游水电站的发电有较大影响，其关系表达式为

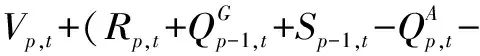
(3)

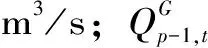
(2)农业供水流量约束。约束条件为

(4)

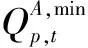
(3)工业及市政供水流量约束。约束条件为

(5)

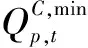
(4)蓄水量约束。约束条件为

(6)

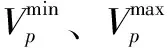
(5)发电流量约束。约束条件为

(7)

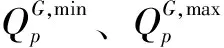
(6)发电出力约束。约束条件为

(8)

3 仿水循环算法

仿水循环算法(WCA)是从大自然水循环及水流动的现象中得到启发提出一种全新的种群优化算法。算法首先随机生成一组初始水滴，其对应的目标函数值为这些水滴的相对海拔高度，进而可以计算出其相对重力，水滴粒子在这相对重力的引导下进行迭代，相对重力较大的水滴粒子拥有更快的迭代速度。在迭代的过程中，WCA模拟水循环中汇流、分流、渗流、蒸发降水过程并构建相应的搜索策略，能根据当前水滴粒子的位置、质量、相对海拔等信息自动调整种群数量及水滴质量。例如在求解优化问题的初始阶段，WCA能汇聚多个水滴粒子的力量集中对某个方向进行搜索，使得算法能较快逼近最优解附近，而在迭代后期，WCA利用分流渗流策略令水滴粒子进行细致的局部搜索。此外，蒸发降雨避免水滴粒子早熟而导致的资源浪费和搜索停滞。

3.1 重力寻优机制

假设最优求解问题为minf(x)，l≤x≤u，其中x为N维向量，上下界分别为l和u。WCA首先计算水滴种群对应的函数值，令其为水滴相对海拔高度。由物理原理可知，水流在重力的影响下从海拔较高处移动至海拔较低处。一般情况下，在优化问题中的最优值在计算前是未知的，因此WCA定义海拔高的水滴始终向着海拔低的水滴进行流动，即朝着当前更优的位置进行移动。此外，当出现多个低海拔水滴时，定义水滴i同时受到它们相对重力的牵引，构建其相对重力的合力为

(9)

式中，B为比水滴i更优的水滴集合；mi为水滴i的质量，初始质量为m0；k为当前迭代次数；f(xi)为水滴i对应的目标函数值。

为了提高水滴迭代的多样性及可行性，在式(11)的基础上加入随机步长，WCA根据以下迭代方程确定水滴的新位置，即

(10)

式中，λg为随机数，λg∈(0，1)。

3.2 汇流策略

在迭代过程中，通过计算水滴间的欧几里得距离及相对海拔差，可对水滴在解空间的相对位置进行判断，进而对位置接近的水滴群进行汇流操作。水滴i、j的欧氏距离计算公式和相对海拔差为

(11)

fd=|f(xi)-f(xj)|

(12)

式中，dij为水滴i、j间的欧氏距离；D为维数；fd为相对海拔。

(13)

xm=xi，best∀i∈NM

(14)

式中，mi为参与汇流水滴的质量；NM为参与汇流的水滴数；mm为汇流后新水滴质量；xi，best为参与汇流的最优水滴位置；xm为汇流后新水滴的位置。

通过汇流策略，WCA能将相近的多个水滴汇聚为一个水滴，这样不仅能增大单个水滴质量，集中搜索资源，加快水滴移动速度，并且还能有效减少水滴种群数量，加快迭代速度。

3.3 分流策略

为避免因汇流策略可能导致的水滴质量过大、种群大小锐减进而收敛早熟的问题，设定当水滴质量超过水滴初始质量的一定倍数时，分流其一半的质量形成一个新的水滴，并赋予新水滴粒子随机的相对重力，即

ms=0.5mi

(15)

Fs=Fi+σsp

(16)

式中，mi为分流水滴的质量；ms为分流后新水滴的质量；Fi为分流水滴的相对重力；Fs为分流后新水滴的相对重力；σsp为N维随机向量。

分流策略是对汇流策略的平衡，起到防止因质量过大造成的收敛早熟的作用，同时分流后随机分布的新水滴也在一定程度上提高了种群多样性。

3.4 渗流策略

模拟水对地表的渗透，构建WCA的渗流策略。在目前搜索到的最优解的临近区域进行随机搜索，探寻可能存在的最优值。其过程可简单描述为依次对全局最优解各维数进行一维小范围随机扰动为

(17)

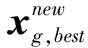
通过渗流策略，WCA能在当前全局最优解旁随机探寻更好的解以替换当前解，该操作能有效提高算法的局部精细搜索能力，提高收敛精度。

3.5 蒸发降雨策略

在WCA迭代过程中，当前最优解xg，best是不断进行更替的，处于xg，best中的水滴由于其相对海拔最低，不再受到其他水滴的相对重力影响，因此会造成搜索资源的浪费。WCA模拟自然界蒸发降雨过程，构建相应搜索策略，将处于相对海拔最低的水滴进行蒸发，按照初始质量m0平均分散为多个水滴并降雨至解空间的随机位置中，重新展开迭代。即

NRF=mg，best/m0

(18)

xRF，i=l+λRF(u-l) ∀i∈NRF

(19)

式中，mg，best为当前最优解的水滴质量；NRF为降雨后生产的水滴个数；λRF为随机数，λRF∈(0，1)；xRF，i为降雨后各水滴的位置。WCA通过式(18)为得到降雨水滴个数，利用式(19)分配新水滴在解空间内的位置。

由于式(9)(10)的重力寻优机制中只需要当前最优解的位置而最优水滴本身并不参与计算，因此对其进行蒸发降雨操作并不影响算法正常迭代。蒸发降雨策略对处于当前最优的水滴进行处理，令其跳出当前位置，该操作能有效防止水滴陷入局部最优解，避免算法早熟，有效利用搜索资源，更能增加水滴多样性，提高算法全局搜索性能。

4 多目标仿水循环算法(MWCA)

假设多目标优化问题可表达为

minf(x)=[f1(x)，f2(x)，…，fM(x)]

(20)

式中，f1(x)，…，fM(x)为多个目标函数；M为目标函数个数。对于此类多目标优化问题，其并不存在全局最优，因此对于WCA不存在唯一的最低海拔点。在此引入Pareto存档进化策略(Pareto Archived Evolution Scheme，PAES)并进行一些改进，提出多目标仿水循环算法，将非劣解集(对应目标函数空间上的Pareto前沿)的点均认为是地形最低点，通过计算非劣解集中水滴的密度信息，令水滴有较大趋势向着密度值较小的区域进行移动，改进后的多目标重力寻优机制可表示为

(21)

式中，NP表示位于非劣解集A的水滴数；ρfront，j为非劣解集内水滴j的密度信息；xfront，j为非劣解集内水滴j的位置；ffront，j为水滴j对应的Pareto前沿点。随后，同样利用式(10)进行水滴的移动。

经过此改进后，各水滴由原先的受到每一个低海拔水滴的吸引，转变为受到非劣解集中所有水滴施加的相对重力。其中非劣解集中密度值低的水滴粒子施加的相对重力较大，密度值高的水滴产生的相对重力较小。改进后的寻优机制防止了水滴朝着单一非劣解移动导致水滴过于集中而陷于局部最优点，进而导致的收敛早熟问题，也避免了水滴被大量非劣解同时引导而致使的搜索缓慢现象。

针对带约束的多目标优化问题，本文采用罚函数法进行处理，即对每一个目标函数加上约束条件的罚函数，则约束下优化问题即可转变为无约束优化。MWCA的算法流程如图1所示。

图1 MWCA算法流程

具体步骤如下：

(1)初始化MWCA水滴种群，包括初始迭代次k=1、最大迭代次数Kmax、种群数量N、水滴群初始位置{x1，x2，…,xN}、初始适应度{f(x1)，f(x2)，…，f(xN)}和初始质量m0、根据PAES生成当前种群的非劣解集A。

(2)根据水滴质量和位置信息，执行汇流、分流、渗流、蒸发降雨策略，利用前文所述流程对水滴质量及水滴种群大小进行自适应调整和优化。

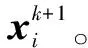
(5)更新水滴群的非劣解集解A，若A中所存储的水滴数达到A的上限时，根据密度信息移除A中密度值最高的一个水滴，并将新水滴存入其中。

(6)重复步骤(2)～(5)，直至达到最大迭代次数，此时存于非劣解集A中的水滴位置就是多目标优化问题的最优解，其对于的适应度就是多目标优化值，列出或画出相应的Pareto边界，决策者就可通过不同的期望选择相应的解。

5 实例应用

5.1 梯级水库群实例

本文利用某流域梯级水库群5个主要电站作为研究实例，其中1号电站为龙头电站，5号电站为末端电站，农业灌溉供水从水库上游的河道区间引水，工业及市政集中供水从各水库中取水，调度期为一年，其中1月～3月为枯水期，6月～8月为丰水期，其他月份为平水期，各水库及电站的装机容量、额定库容、正常水位等参数如表1所示。

表1 梯级水电站参数

表2 各算法非劣解及耗时对比

5.2 算法对比分析

为验证MWCA算法的有效性与优越性，采用MOPSO算法[19]和NSGA-II算法[20]进行对比分析，对上述研究实例进行优化调度计算。仿真环境为配置i5-2520M、16G内存的联想T420笔记本电脑，各算法分别独立进行10次运算，其所有的非劣解在目标函数空间所对应的Pareto边界如图2所示。由图2可知，3个算法的都具有较好的收敛稳定性，但MWCA所得非劣解的Pareto边界分布更广、更均匀。尤其是在年均发电量大于300亿kW·h的区域内，MWCA搜索到了大量的非劣集，而MOPSO和NSGA-II在这一区域仅得到少数的解。此外，整体Pareto边界也比另两个算法更优，例如图2中当年均发电量为240亿kW·h时，MWCA非劣解的调度策略能提供116.5亿m3的年均供水量，而MOPSO与NSGA-II仅能提供约116亿m3的供水量，相比MWCA减少了0.5亿m3。另一方面，当年均供水量为117亿m3的时候，MWCA可获得约210亿kW·h的年均发电量，与之相比MOPSO与NSGA-II的发电量仅180亿kW·h左右。这说明在同等求解目标及约束函数下，MWCA能在各个目标下均获得比NSGA-II算法与MOPSO算法更好的求解性能和更优的非劣解。这得益于MWCA的渗流与蒸发降雨策略，有效的提高了水滴种群的多样性，同样也增强了MWCA的局部寻优性能，使其获得了更多的非劣解。各算法10次独立计算的多目标优化结果最大值、最小值、非劣解数量、耗时等如表2所示。

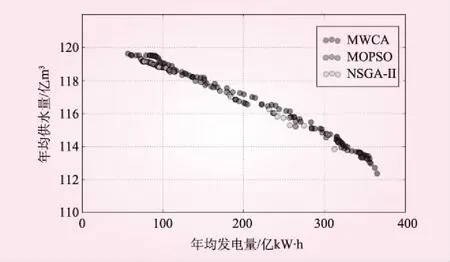
图2 各算法独立10次运算后所得的Pareto边界

由表2可知，MWCA所得到的调度策略能获得最高367.16亿kW·h的年均发电量，相比MOPSO的358.41亿kW·h和NSGA-II的313.15亿kW·h分别多出了8.75亿kW·h和54.01亿kW·h的发电量。同时MWCA所得的最大年供水量119.64亿m3也比MOPSO和NSGA-II的多出了0.58亿m3和0.32亿m3。此外，MWCA所得非劣解的年均最小年均发电量比NSGA-II与MOPSO更小。这表明MWCA所获得的非劣解范围更广，搜索性能更强。经过10次独立运算后，MWCA能获得84个非劣解，与此同时MOPSO与NSGA-II仅分别获得51个和48个非劣解。在计算耗时上，MWCA、MOPSO和NSGA-II平均为11.07、9.82 s和11.50 s。虽然MWCA耗时并非最少，但利用相近的时间，MWCA获得了多于另两个算法的非劣解数量，体现了该算法在迭代速度和和性能上的优越性。

为进一步分析算法所得非劣解的分布特性，本文采用分布距离指标(SD)[19]及超体积指标(HV)[21]进行高阶评价。其中分布距离指标用于分析非劣解分布的均匀性，其计算式为

(22)

式中，ds，i为非劣解两两间的距离，ds，i=minj|f1(xi)-f1(xj)+f2(xi)-f2(xj)|，i，j=1，2，…，nnd；ds，avg为ds，i的平均值；nnd为所得非劣解的数量。该值越小，则所有非劣解两两间的距离越一致，即实现非劣解的平均分布。本文算例中3个算法的SP值如表3所示。

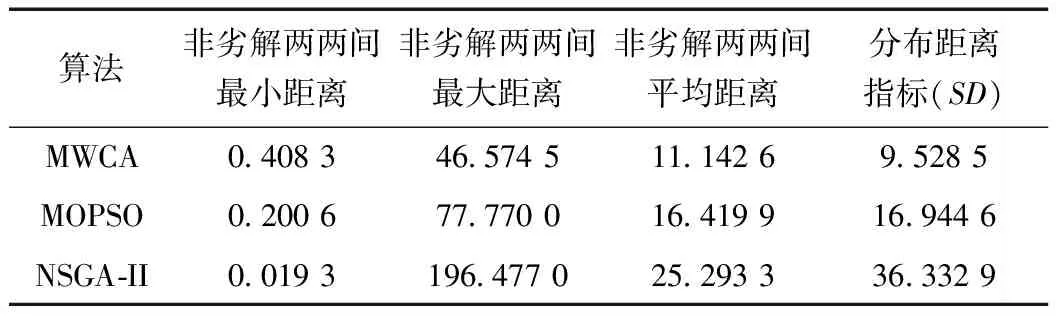
表3 各算法非劣解及耗时对比

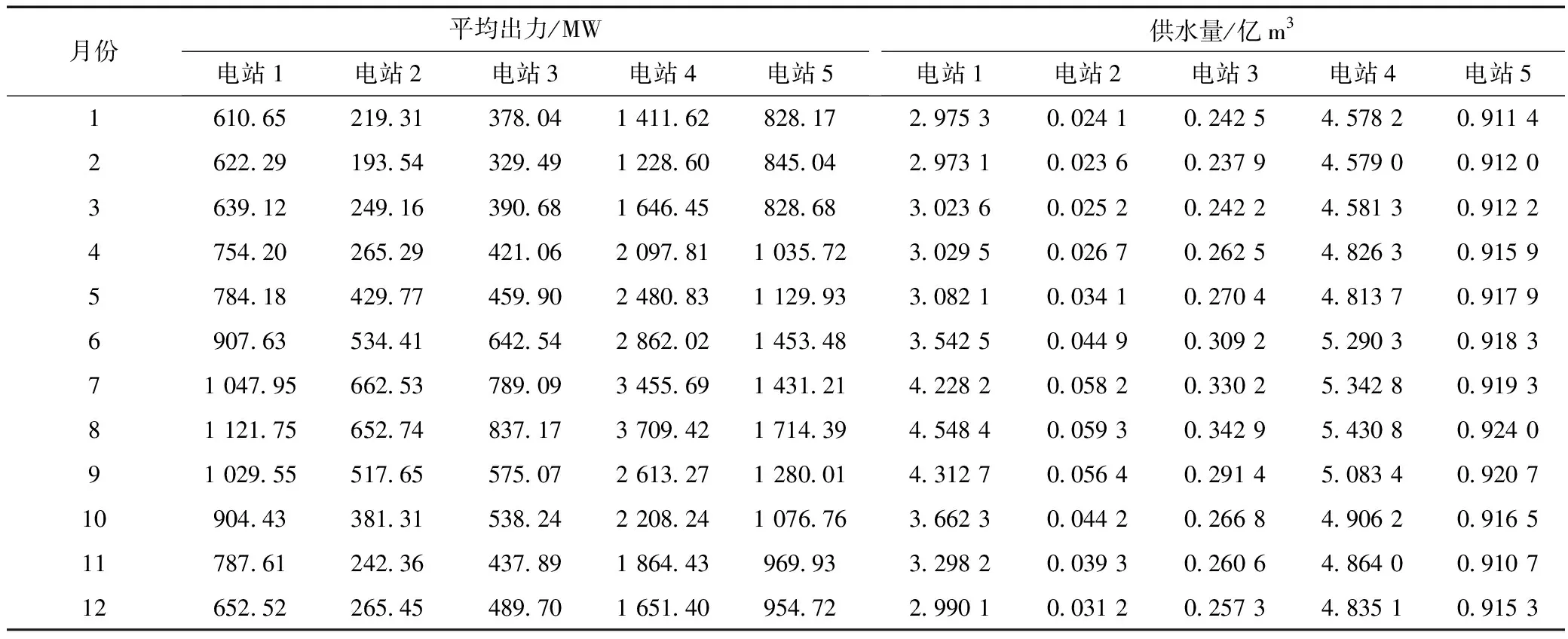
表4 MWCA优化调度结果

可见MWCA算法所得非劣解的分布距离指标为9.528 5，远小于MOPSO算法和NSGA-II算法，说明了MWCA非劣解的分布更为平均。此外MWCA较小的平均距离也同样证明了这点。

超体积指标利用非劣解在多目标函数空间上所围成的超空间体积(面积)作为评判标准，本算例三个算法所得非劣解的超体积示意及数据如图3所示。由图3可知，MWCA算法所得超体积指标为199.63，明显大于MOPSO算法的132.84及NSGA-II算法的99.67。通过分布距离指标和超体积指标的高阶分析，MWCA同样显示出了优于另两个算法的均匀性和宽广性，这再次验证了本文算法优越的多目标优化性能。

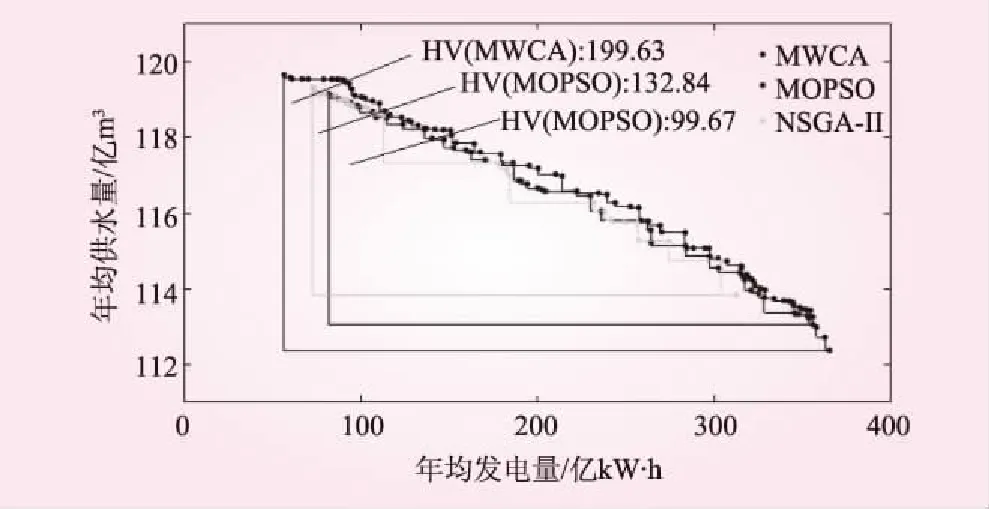
图3 各算法的超体积指标(HV)示意

5.3 MWCA调度结果分析

由于处于Pareto边界的非劣解均为多目标优化问题的有效解，对非劣解的选择取决于决策者的调度策略偏好，有的希望提高发电量，而有的希望增加供水量。本文不对调度策略的偏好进行研究，因此选取发电量与供水量较为均衡的一组非劣解进行分析，如表4所示。

由表4可知，各电站的出力与枯水期和丰水期的趋势一致，在来水较少的1月～3月，各电站平均出力都比6月～8月低。在供水量方面，不论在枯水期还是丰水期，MWCA所得非劣解给出的调度策略都能保证较好的供水量，即使在枯水期的1月～3月，各水库及其上游河道区间仍保持了较好的供水能力。相较平均出力的较大变化，供水量的浮动并不大，这一方面是由于水库群的蓄水功能保证了一定的供水量，另一方面则是通过降低水电站出力进行了一定妥协。在枯水期的情况下，削减水电站出力，保证最低供水量及死水位约束。此外，这也体现了“蓄丰补枯”的补水调度作用，在丰水期来临之时多蓄水，便能在枯水期到来时提供足够的供水量满足工业和民生需求。上述调度策略显示了MWCA应用于梯级水库群优化调度的合理性与有效性。

6 结 论

本文针对梯级水库群调度问题，构建了发电量最大和供水量最大的多目标优化调度模型，提出了多目标仿水循环算法MWCA，引入了汇流、分流、渗流、蒸发降雨4个优化策略对水滴种群进行处理，能有效提高种群多样性、提升搜索性能、加快收敛速度、防止陷入局部最优、避免迭代早熟等，针对多目标优化问题，构建了新的重力迭代和寻优机制。实例应用结果验证了MWCA在水库群多目标优化调度问题中的合理性和可行性，同时也表明了MWCA相比MOPSO和NSGA-II的搜索性能更强，非劣解多样性更好、分布更均匀和宽广，具有较好的研究和工程应用前景，为梯级水库群多目标优化调度问题提供了一种有效的解决方案。