基于库水作用分区的浮托减重型滑坡稳定性分析
史丁康,许万忠,熊茹雪,张 钧,梁为邦,苏东院
(1.昆明理工大学国土资源工程学院,云南 昆明 650093;2.云南省水利水电勘测设计研究院,云南 昆明 650021)
0 引 言
我国水力资源丰富,修建了众多大型水库。其中,以三峡水库为最,水库总面积1 084 km2,库水位在高程145~175 m之间变化,如此大的水位变幅带势必会造成众多库岸边坡失稳。库岸边坡失稳主要造成以下3种危害[1]:大方量山体滑入水库减少库容,甚至使水库废弃;滑坡摧毁大坝等水工建筑物;山体迅速下滑造成巨大涌浪,直接危及下游人民生命财产安全。晏鄂川[2]以滑体组构特征、动力成因、变形运动特征和发育阶段这4个控制性因素,建立滑坡综合分类体系。肖诗荣[3]根据滑坡诱发机理,将三峡水库滑坡分为库水浮托型、动水压力型、库水软化型等3类。朱大鹏[4]研究了浮托减重型和动水压力型滑坡变形对库水位变动的响应关系,进而分析库水作用下不同动力成因的滑坡稳定性变化规律。赵代鹏[5]建立浮托减重型滑坡物理模型,并与数值模拟相结合,揭示在库水位升降作用下滑坡力学机制与稳定性变化规律。王世梅[6]、邓永煌[7]等对不同库水位升降速率作用下的浮托减重型滑坡进行稳定性分析。
现有研究多是在确定的库水作用区域,从库水位升降速率的角度分析浮托减重型滑坡的稳定性。本文应用Geostudio有限元软件中的seep/w模块与slope/w模块耦合分析,探究不同库水作用分区的浮托减重型滑坡稳定性变化规律,为库区浮托减重型滑坡预测评价提供参考。
1 浮托减重型滑坡
库水位升降对库岸滑坡稳定性的影响主要体现在基质吸力改变、软化作用、浮托减重作用、动水压力作用、冲蚀作用、超孔隙水压力、水库诱发地震等方面。其中,浮托减重作用是库岸滑坡普遍受到的影响,只要有水渗入滑坡体,该滑坡就一定受到浮托减重作用。但是,库水对滑坡稳定性的影响以浮托减重作用为主的滑坡才称之为浮托减重型滑坡。浮托减重型滑坡显著的特点是渗透性较好,或饱和渗透系数与库水位升降速率的比值较大,坡内地下水能及时随库水位变化而变化,进而影响坡内有效应力的大小。
一般典型的库岸边坡为二元结构边坡[8],即上层为土层,下层为岩层,其潜在滑移面为土岩交界面;且边坡土岩交界面下部倾角较缓甚至反倾,为抗滑段,土岩交界面上部倾角较陡,为下滑段。即使是均质边坡,其潜在滑移面(圆弧滑动或折线滑动)一般也是下部较缓为抗滑段,上部较陡为下滑段。库水位在边坡不同部位升降时,边坡岩土体的受力状态是不同的。
库水入渗后,岩土体有效容重由天然容重减小为浮容重,对岩土体有减荷的作用,即浮托减重。岩土体有效质量减小对边坡稳定性有2方面的影响[9],一方面,顺坡方向重力分量——下滑力减小,提高边坡稳定性;另一方面,垂直于滑移面的重力分量——正压力减小,导致其所能提供的抗滑力减小,降低边坡稳定性。应当注意到,边坡岩土体有效质量变化一定时,抗滑段岩土体的抗滑力变幅大于下滑力,下滑段岩土体的下滑力变幅大于抗滑力。因此,随着浸润线的变化,浮托力作用于边坡的不同区域,对边坡稳定性影响机制是不同的。
2 计算理论
2.1 饱和-非饱和渗流微分方程
由于滑坡体浸润线以上处于非饱和、浸润线以下处于饱和状态,随着库水位的涨落,滑坡体中的地下水位也随之发生变化,在滑坡体中形成了土体的非饱和区和饱和区。非饱和区土壤水运动和饱和区地下水的运动是相互联系的,将两者统一起来即为饱和与非饱和流动问题。二维饱和-非饱和渗流的一般控制微分方程[10]可由Darcy定律和质量守恒定律联合推导得出,当采用水头作为控制方程的因变量时,渗流微分方程为
(1)
式中,H为总水头;kx为x方向的渗透系数;ky为y方向的渗透系数;Q为施加的边界流量;mw为比水容重,是体积含水量驻留曲线的斜率;γw为水的容重;t为时间。
2.2 渗透系数函数
在饱和-非饱和条件下,土体渗透系数不是一个常数。由于非饱和土孔隙中充填空气,使水的渗流路径变得曲折,阻碍了水的流动,致使土体渗透系数变小,所以非饱和土渗透系数是基质吸力或体积含水量的函数。直接测量非饱和土渗透系数函数比较困难,但可以通过由土-水特征曲线与饱和渗透系数推导出非饱和渗透系数函数的方法来解决。1994年,Fredlund提出了一种渗透系数拟和方法,该方法的控制方程为
(2)
式中,kw为指定含水量或负孔隙水压力计算所得渗透系数;ks为测得的饱和渗透系数;θs为饱和体积含水量;y代表负孔隙水压力算法的虚拟变量;i为j到N之间的数值间距;j为最终函数描述的最小负孔隙水压力;N为最终函数描述的最大负孔隙水压力;ψ为对应第j步的负孔隙水压力;θ′为体积含水量的一阶导数。
2.3 非饱和土抗剪强度理论
Fredlund[11]非饱和土抗剪强度公式为
s=c′+(σn-ua)tanφ′+(ua-uw)tanφb
(3)
式中,s为非饱和土抗剪强度;c′为有效粘聚力;(σn-ua)为净法向应力;ua为孔隙气压力;φ′为有效内摩擦角;(ua-uw)为基质吸力;uw为孔隙水压力;φb表示抗剪强度随基质吸力而增加的速率。非饱和土的抗剪强度由粘聚力、内摩擦角和基质吸力贡献值3部分组成,分别为粘聚强度、摩擦强度和吸力强度。
作为φb的替代,Vanapalli[12]等给出了方程
(4)
式中,θw是体积含水量;θr是残余体积含水量。在slope/w中,残余体积含水量假定为饱和体积含水量的10%。土的非饱和抗剪强度参数可利用基于土-水特征曲线和饱和抗剪强度参数的方法来估算。
3 数值计算
3.1 计算模型
基于库水作用分区方法,构建浮托减重型滑坡,见图1。图1中,ab段为滑坡体的下滑段,bc段为滑坡体的抗滑段[13]。以库水位变动作用区域为依据,将滑坡划分为A、B、C等3个库水作用区域,库水位在A区变动时仅作用于抗滑段,在B区变动时同时作用于抗滑段与下滑段,在C区变动时仅作用于下滑段。
为研究不同库水作用区域对浮托减重型滑坡稳定性的影响,对应A、B、C这3个库水作用区域,应用GeoStudio软件建立3类典型浮托减重型滑坡计算模型,见图2。网格类型为三角形与四边形网格,网格合计7 746个节点,7 673个单元。

图2 计算模型与有限元网格划分
3.2 计算参数
本文选取谭家河浮托减重型滑坡[6]计算参数,seep/w模块材料模型选择饱和/不饱和;slope/w模块材料模型选择理想弹塑性M-C本构模型。岩土体物理力学参数见表1。

表1 岩土体的物理力学参数
边坡内浸润线以下为饱和区,浸润线以上为非饱和区,土体非饱和特性有利于边坡稳定。土-水特征曲线(SWCC)与渗透系数函数是非饱和-非稳定渗流分析的2个必不可少的参数。土-水特征曲线采用seep/w模块内置的样本函数估计,只需要输入各岩土层的饱和体积含水量,就可以得到其土-水特征曲线,见图3。渗透系数函数采用Fredlund&Xing估计方法,通过饱和渗透系数与土-水特征曲线来预测非饱和土渗透系数函数,见图4。
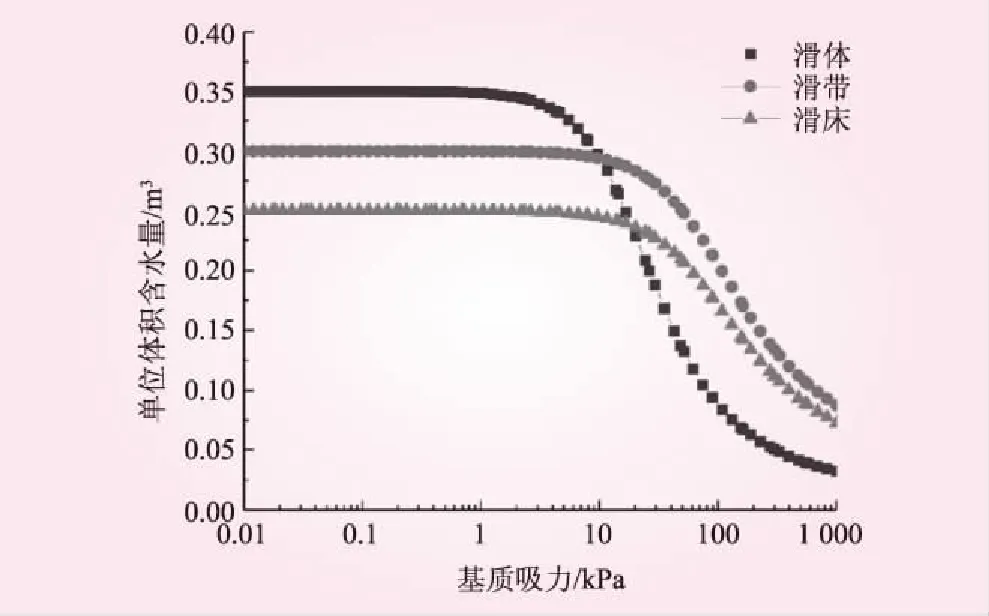
图3 土-水特征曲线

图4 渗透系数函数
3.3 计算工况
为研究不同库水作用区域对浮托减重型滑坡稳定性的影响,建立了3类典型浮托减重型滑坡计算模型,每类计算模型均进行库水位升降模拟,库水位升降速率分别取0.5、1.0、2.0 m/d这3种工况。
3.4 计算步骤
应用GeoStudio有限元计算软件,在seep/w模块进行库水位升降条件下库岸边坡渗流场分析,初始状态采用稳态分析,库水位升降过程中采用瞬态分析。然后将seep/w模块渗流场计算结果导入到slope/w模块,采用Morgenstern-Price法进行边坡稳定性分析。
4 结果与分析
4.1 库水位升降仅作用于抗滑段
库水分别以3种不同速率作用于A区,不同库水升降速率下浸润线变化见图5。图5中,1、2、3分别表示库水位升降速率为0.5、1.0、2.0 m/d。从图5可知,滑体内浸润线均随库水位的上升而上升,库水位上升速率越慢,浸润线越缓,水力梯度越小,指向坡内的动水压力越小,相应稳定性系数越小;滑体内浸润线均随库水位的下降而下降,库水位下降速率越快,浸润线越陡,水力梯度越大,指向坡外的动水压力越大,相应稳定性系数越小。

图5 不同库水升降速率下浸润线变化

图6 不同库水升降速率下稳定性系数变化
不同库水升降速率下稳定性系数变化见图6。从图6可知,库水位上升速率越慢或库水位下降速率越快时,滑坡稳定性越差。滑坡整体稳定性随库水位的上升而下降,库水位达到60 m时稳定性系数最小。滑坡整体稳定性随库水位的下降而上升,库水位达到40 m时稳定性系数最大。这是由于库水位在A区上升时,抗滑段浮托力增大,抗滑力比下滑力减小得多,所以滑坡稳定性系数减小;库水位下降时,抗滑段浮托力减小,抗滑力比下滑力增加得多,所以滑坡稳定性系数增大。因此,A区浮托力不利于滑坡稳定。
4.2 库水位升降仅作用于下滑段
库水位分别以3种不同速率在C区升降,不同库水升降速率下浸润线变化见图7。图7与图5浸润线变化规律相同。
不同库水升降速率下稳定性系数变化见图8。从图8可知,库水位上升速率越慢或库水位下降速率越快时,滑坡稳定性越差。滑坡整体稳定性随库水位的上升而上升,库水位达到120 m时稳定性系数最大。滑坡整体稳定性随库水位的下降而下降,库水位达到100 m时稳定性系数最小。这是由于库水位在C区上升时,下滑段浮托力增大,下滑力比抗滑力减小得多,所以滑坡稳定性系数增大;库水位下降时,下滑段浮托力减小,下滑力比抗滑力增加得多,所以滑坡稳定性系数减小。因此,C区浮托力利于滑坡稳定。
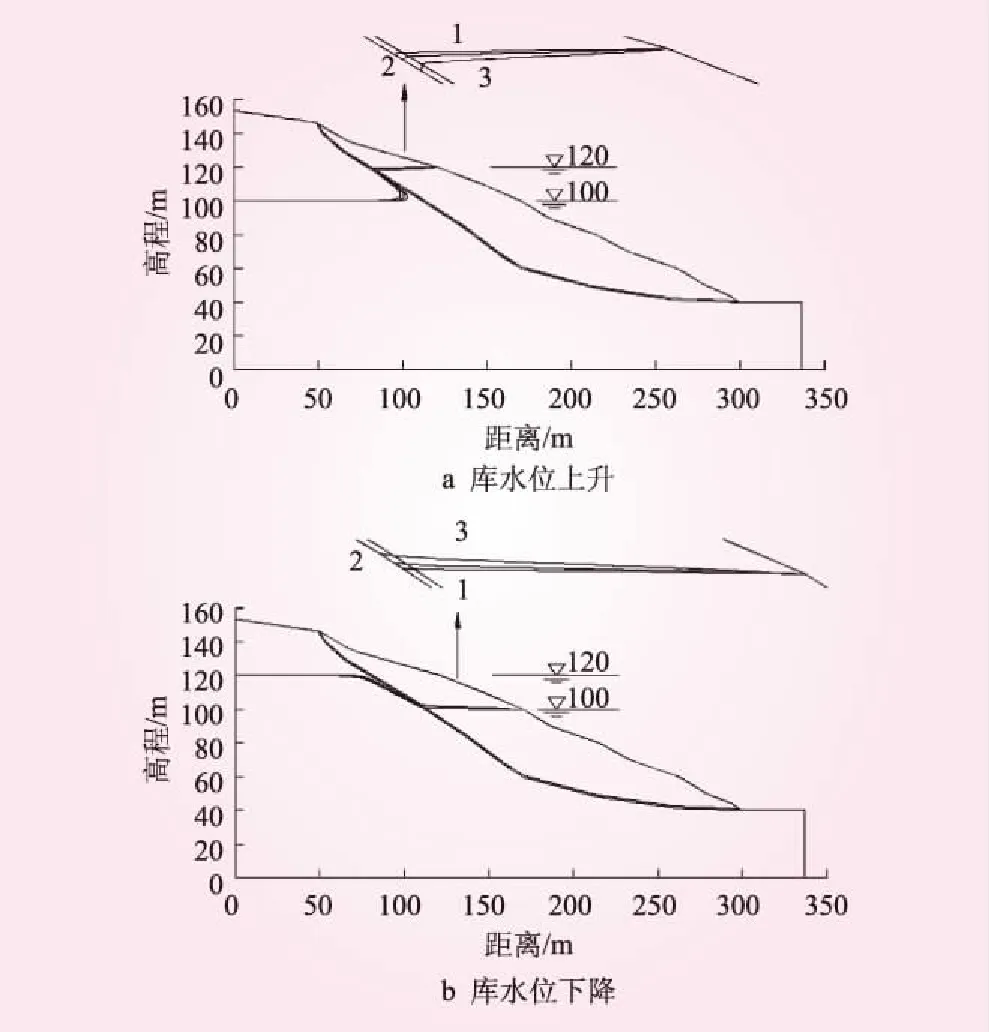
图7 不同库水升降速率下浸润线变化
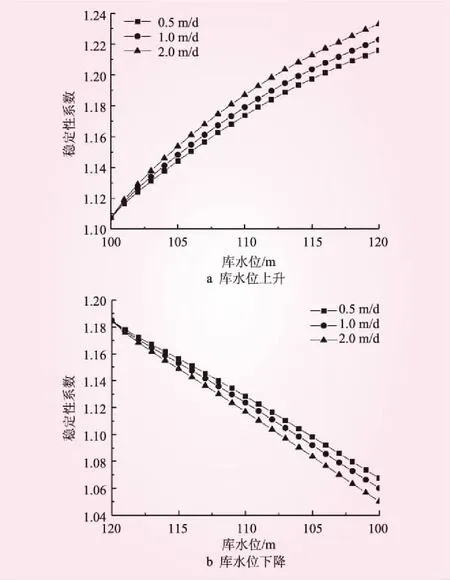
图8 不同库水升降速率下稳定性系数变化
4.3 库水位升降同时作用于抗滑段与下滑段
库水位分别以3种不同速率在B区升降,不同库水升降速率下浸润线变化见图9。图9与图5浸润线变化规律相同。
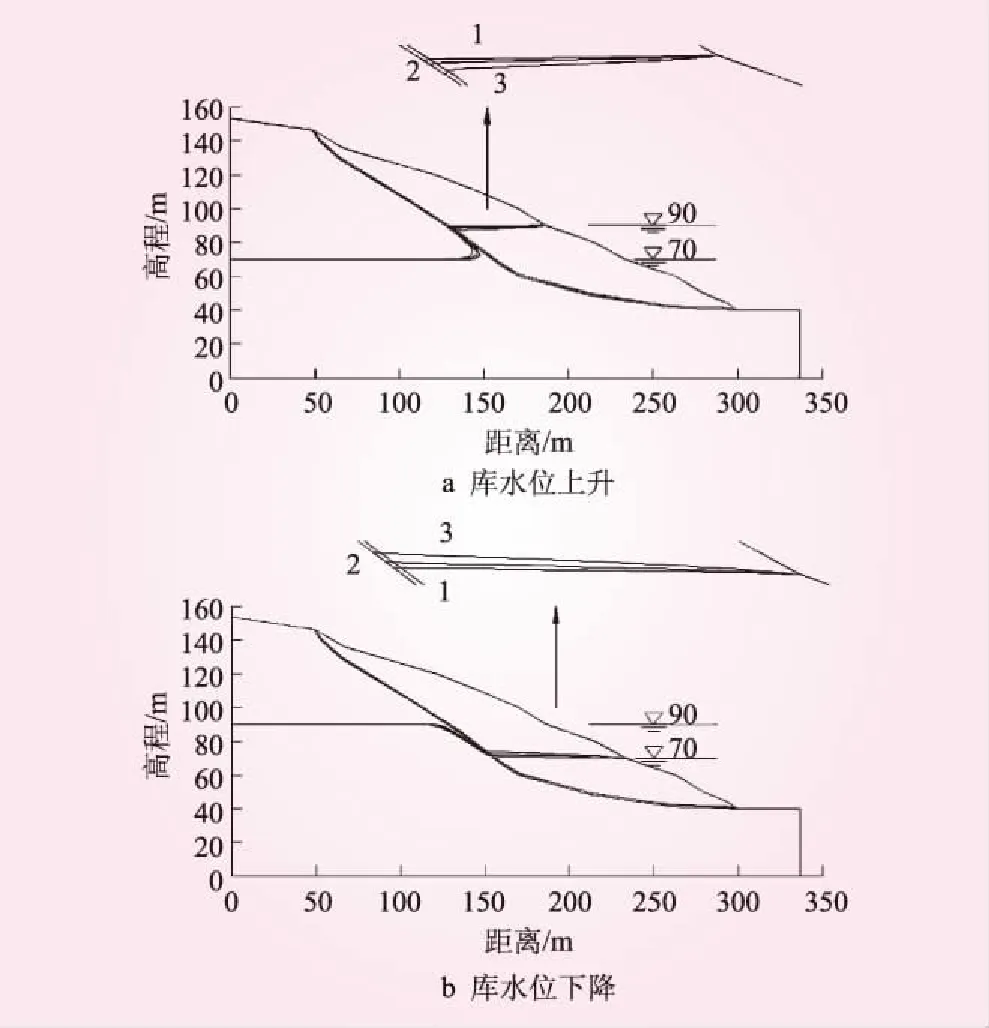
图9 不同库水升降速率下浸润线变化
库水作用于B区,库水位升降同时作用于抗滑段与下滑段,浮托力对抗滑段与下滑段影响的力学机制正好相反,部分影响抵消,所以B区浮托力对滑坡稳定性的影响较小,易受动水压力的影响。为减小动水压力的影响,放慢库水位升降速率,计算滑坡稳定性时,增加库水位升降速率为0.1 m/d的工况。4种不同库水升降速率下稳定性系数变化见图10。从图10可知,库水位上升速率越慢或库水位下降速率越快时,滑坡稳定性越差。库水位上升时,不同库水位上升速率的滑坡整体稳定性变化规律有所差异。升速为0.1 m/d时,表现为浮托减重型,开始时刻库水主要作用于抗滑段范围,随着库水位的上升,下滑段受到的浮托作用范围变大,所以稳定性系数先减小再增大,但稳定性系数变化范围很小(只有0.013),这正是抗滑段与下滑段浮托减重作用相互抵消的结果。升速大于等于0.5 m/d时,表现为动水压力型,指向坡内的动水压力使稳定性系数一直增大。库水位下降时,滑坡整体稳定性先下降而后上升,降速越小稳定性系数上升趋势越明显,即浮托减重效应越明显。
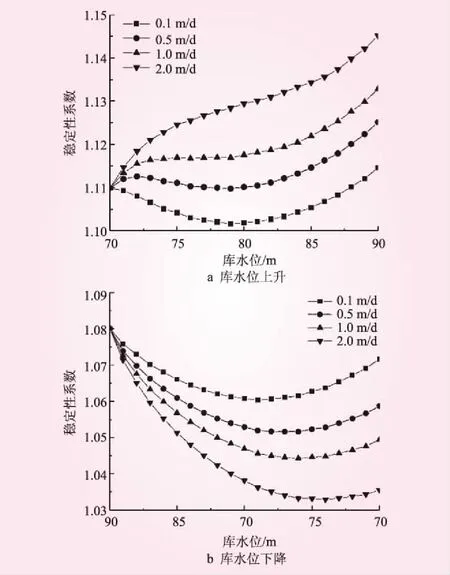
图10 不同库水升降速率下稳定性系数变化
综上,库水位升降条件下,在浮托减重型滑坡A区升水、B区和C区降水时,滑坡整体稳定性系数减小,最不利于滑坡稳定,应加强在这3种工况下的滑坡变形监测预报。
5 结 语
本文以库水位变动作用区域为依据,将滑坡划分为A、B、C等3个库水作用区域,研究不同库水作用区域对浮托减重型滑坡稳定性的影响。结果表明,滑坡稳定性系数对不同库水作用分区的响应也不同:
(1)库水作用于A区时,浮托力不利于滑坡稳定,滑坡整体稳定性随库水位的上升而下降,滑坡整体稳定性随库水位的下降而上升。
(2)库水作用于B区时,浮托力对滑坡稳定性的影响较小,即滑坡稳定性系数变化范围较小,易受动水压力的影响。当库水位升降速率较慢时,滑坡整体稳定性均为先下降后上升。
(3)库水作用于C区时,浮托力利于滑坡稳定,滑坡整体稳定性随库水位的上升而上升,滑坡整体稳定性随库水位的下降而下降。
(4)库水位升降条件下,在浮托减重型滑坡A区升水、B区和C区降水时,滑坡整体稳定性系数减小,最不利于滑坡稳定,应加强在这3种工况下的滑坡变形监测预报。
(5)不同库水作用分区的滑坡稳定性计算结果符合浮托减重型滑坡稳定性变化规律,不同库水位升降速率导致的稳定性差异是由于动水压力产生的。不论库水作用在滑坡何区域,均表现为库水位上升速率越慢或库水位下降速率越快时,滑坡稳定性越差。

