水平轴水轮机叶片翼尾弯角对水动力性能的影响研究

岑昱昕，王世明，李泽宇

(上海海洋大学工程学院，上海 201306)

0 引 言

叶片在影响水轮机水动力性能的诸多要素中占有非常关键的地位，对于叶片设计方法的研究以及叶片翼型的优化，一直都是从事水轮机研究的人们最为关心的问题。中国虽然海岸线长，海洋资源丰富，但能量较分散，造成目前应用于海洋能捕获的水轮机叶片获能效率不理想，进而影响海洋能发电装置的功率[1-2]。随着单机功率的不断提高，水轮机在面对来流时，叶片翼尾同时受到水动力和结构力，其朝向和弯曲角度直接影响流场和水动力环境的优劣，故而成为决定轮机性能的关键部位[3-5]。但到目前为止，对于叶片翼尾弯角的变化带来的叶片水动力性能的影响，无论是计算机数值模拟还是洋流实验研究，都还远远不够。

图1 翼型变形示意

本文选取NACA0014标准翼型，利用Fluent流体仿真软件和翼型X-foil设计软件，对不同翼尾弯角对叶片要素产生的影响，以及对其水动力性能的影响进行了研究，并设计实验对仿真结果进行验证，得到了较准确的结论，为翼型进一步优化研究提供参考。

1 水轮机叶片翼型分析

过大的弯角容易使翼型产生额外的阻力，其出流速度的方向与水平轴方向的夹角应当远小于90°，否则会引起较严重的反流，极大增加了轴向载荷。另外，翼型尾缘弯角的设置，应当避免使流体的边界层产生紊流从而增大运动阻力，减少流体振动的产生。因此弯角应当控制在一个比较小的范围内。

利用X-Foil程序能够对已有翼型进行变形处理，如图1所示，对NACA0014翼型添加挠度，变形轴线方向位置设定为以翼型前缘为坐标原点的0.75处，纵向方向位置设定为上半翼与下半翼的中心，对原始翼型的尾部沿纵向分别上弯10°、5°以及下弯5°、10°、15°，基于原始翼型变形得到的一组共6个翼型。

2 模型验证与计算条件

2.1 计算模型与算法

本文数值计算选用标准k-e湍流模型。标准k-e湍流模型在单方程的基础上，添加一个与湍流动能耗散率e相关的方程，其适用范围广，有合理的精度。求解算法选为SIMPLEC算法，此算法是对求解压力耦合方程组的半隐式方法的改进，改变了压力修正项中的部分系数，具有加快迭代过程收敛的优点。

2.2 网格划分与计算条件

本文对计算流场进行结构化网格划分，如图2所示，半圆形区域半径为15 d，是入流区；矩形区域长为25 d，宽为30 d，是流场尾迹区，d为弦长。翼型附近的网格作加密处理，翼型边界与尾部放大网格如图3、图4所示。对边界条件进行设置，半圆弧为速度入口，尾迹后方直线设为自由流出口，矩形区域上下两边界设置为对称边界，湍流模型设置为标准k-e模型。

图2 计算流场与整体网格

图3 翼型局部网格

图4 翼尾放大网格

3 计算结果分析

3.1 升阻力系数分析

图5与图6为不同攻角下升阻力系数的变化情况。攻角变化范围设定为-5°～20°，分别对下弯15°、10°、5°和上弯5°、10°以及原始翼型进行了考查。

图5 升力系数随攻角变化曲线

由图5得知，在-5°～20°攻角范围内，下弯翼型升力系数较原始翼型有所提高，而上弯翼型则正好相反，且随着弯角增大，与原始翼型间的差距也增大。表1则给出了相较于原始翼型，变形翼型在升力系数上的变化量。

表1 变形翼型与原始翼型之间的升力系数变化情况

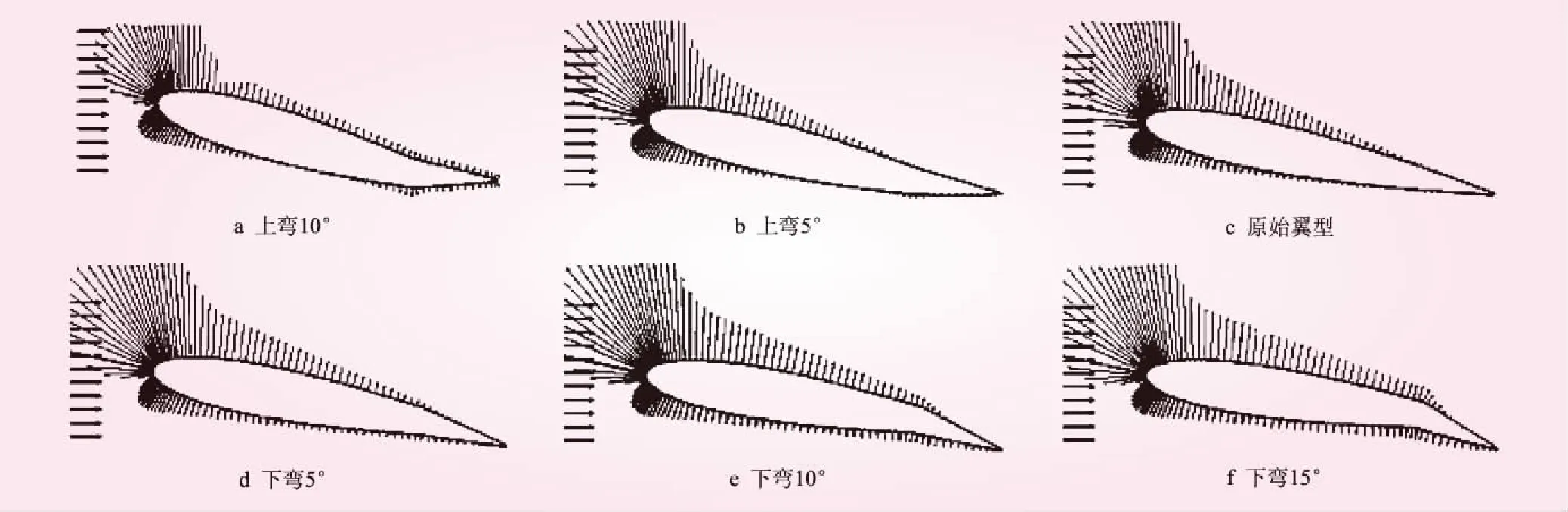
图7 压力系数环绕示意

从曲线来看，在攻角-5°～10°的范围内，升力曲线基本保持线性，此时翼型表面流体为完全附着流动，而当攻角增大，在10°～20°范围内，曲线呈现非线性，翼型表面流体发生部分分离；6种翼型升力系数均随攻角增大呈现上升趋势，当攻角大于10°时，多数曲线上升趋势放缓。

图6 阻力系数随攻角变化曲线

由图6得知，当攻角为0°时，变形翼型阻力系数相比于原始翼型差异最小，随着攻角增大，在5°～20°范围内，阻力系数差异逐渐明显。在-5°～5°攻角范围内，变形翼型与原始翼型之间的阻力系数差处于0.004～0.11之间，而当攻角在5°～20°之间时，阻力系数差就达到了0.135～0.261。

原始翼型最小最大阻力系数分别为0.009和0.27，而经过尾缘下弯的翼型最小最大阻力系数和分别可以达到0.02和0.45，所以当升力系数变化相同值时，下弯翼型阻力系数值要更小一点。

3.2 静压力系数对比分析

图7分别为攻角12°下原始翼型与5种变形翼型的压力系数环绕示意图。可以看出：每个翼型前、后缘点的压力系数梯度最大，随着翼尾向下弯曲变形的程度的增加，其上下表面压力系数差也越来越大，最大压差为各个翼型上下表面的压力系数最大差值，当翼型分别上弯10°、5°时，最大压差相应为2.25、2.5；当翼型分别下弯5°、10°、15°时，最大压差相应为2.95、3.25、3.5。对比图7a与图7f，可以看出，翼尾下弯能够有效地提高压差，从而进一步提高升阻比。

3.3 流动特性对比

图8展示了翼尾变形后其流动分离特性的变化。

图8 翼型流动分离特性图

从图中可以看出，在12°攻角下，翼型上弯5°、上弯10°和原始翼型均呈现出良好的流体附着性，未见出现流动分离；而所有的下弯翼型均出现不同程度的分离特征，其程度随着下弯角度增大而增大。

两种上弯翼型，流线整体上较为致密；原始翼型在尾部出现轻微稀疏，但并未影响后面流场的紧密性；下弯5°后，翼型中后部出现流线稀疏的现象，并在尾部附近最为明显；下弯10°后，翼尾的流线稀疏现象明显，且向后方蔓延；下弯15°后，翼型中后方流动分离现象严重，且造成后方相当大的范围内流体发生分离，附着性受到较大影响，出现失速现象。

结合上述三种参数的分析，NACA0014原始翼型在攻角-3°～17°内具有较高升阻比，翼尾下弯5°、10°和15°后升阻力系数均见明显提高，且随下弯角度增加而增大，升阻比峰值也随之增大，而翼尾上弯则效果相反，升阻力状况均受到消极影响。另一方面，尾部下弯也导致翼型的流动特性出现下降，下弯角度的增大使出现流线分离的临界攻角提前，翼型完全附着流动受到影响，进而导致水轮机叶片常速运转范围减小，更易出现失速现象；上弯翼型流体附着性良好，但良好区间在攻角-2°～14°中，较原始翼型区间长度降低，加之其升阻比受到较大影响，总体性能要比原始翼型差。

4 实验验证

4.1 实验布置

实验轮机的叶片数为4，叶轮直径0.25 m，尖速比为5.5，扫掠面积为0.053 3 m2，安装角43°，导流罩喉部直径0.27 m，扩口张角20°。实验设置在东海标准计量中心的实验室中，将安装不同弯角叶片的轮机置于水槽中，当水流冲击时，水轮机主轴转动，可以得到不同叶片下轮机的功率。同时，水轮机后接实验室的潮流能发电系统的监控设备，可对水轮机产生电能的情况进行电脑终端实时监控，观察弯角改变对轮机性能带来的影响。实验工况与监控设备如图9所示。

图9 实验布置示意

4.2 实验结果分析

不同翼型叶片的轮机功率如图10所示，可以看出：

(1)就不同翼型叶片而言，翼尾下弯程度越大，其性能越好，且随着翼型下弯角度增大，相邻曲线间增幅变大，同长度速度区间内，下弯翼型功率曲线斜率更大，增长更快，最大功率值更高，下弯15°翼型样机在2 m/s流速下可达到最大功率176 W。

(2)翼尾弯角变化引起叶轮最小启动速度变化，下弯愈大，最小启动速度愈小，其自启动性能愈高，适合流速范围更广。对比上弯10°和下弯15°两种翼型，最小启动流速增幅在0.5 m/s左右。

综上分析，实验结果基本与数值计算结果相符，即翼尾下弯能够提高叶片水动力性能，相比于原始翼型，上弯叶片则表现更差。

图10 流速-功率实验曲线

5 结 论

以NACA0014对称翼型作为基础，利用翼型 X-foil设计软件进行尾部弯曲，得到五种变形翼型，并用CFD软件对其进行仿真模拟，针对升阻力系数、静压系数和流动分离特性三个方面进行研究，总结出了不同攻角下翼尾弯曲对卧式水轮机叶片水动力性能的影响。

(1)当攻角较小时，尾部下弯翼型在升力系数上有较大提升，而阻力系数变化较小，使得升阻比更大；当攻角较大时，升力系数仍旧随弯角增大而继续增大，阻力系数虽有增加，但升力系数峰值也相应提高，升阻比情况相比原始翼型仍有改善。

(2)翼尾下弯使得其上下表面压力系数差增大，且翼型前、后缘点的压力系数梯度最大。翼尾每下弯5°，压差可增加0.25左右。

(3)翼尾下弯能够降低轮机最小启动速度，提高轮机自启性能。

(4)下弯翼型更易出现流动分离，程度随弯角增大而增大，弯角大于5°时，分离现象有逐渐向后方流场蔓延的趋势。当攻角较大时，出现失速现象，进而导致阻力增大。

(5)两种上弯翼型升阻力特性及流动分离特性均比原始翼型差，故其水动力性能变差。