借助思维导图，演绎精彩课堂

■福建省安溪县第十六小学 潘翠菊

“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学。”数学如此重要，作为一名数学教师，如何让孩子爱上数学，如何把课堂演绎得更精彩，是我一直以来的追求。从教20 多年来，我经历过一次次的磨课，一次次的评课，一次次的反思。在这个历程中，我深刻地体会到以“思维导图”这种新的呈现方式建构新知，整理旧知，解决问题等方面具有事半功倍的效果。因为思维导图是放射性思维的表达，是一种可视化的思维工具，它可以实现协助记忆、启迪人的灵感、激发人的创造力。那么，如何借助思维导图，演绎精彩课堂呢？

一、借导图，“助”自主建构

在第一学段和第二学段的课程内容中，都涉及数学概念，对它的学习和理解是学习数学的起点，这些大大小小的概念构成了孩子以后掌握整个数学理论体系的基础。学生对概念的理解能力越高，后续学习也就越顺利。但数学概念非常单调，枯燥，无味，如果在新概念的学习过程中，能引入思维导图，可以使学生明确当前所学概念在原有知识基础上的发生发展过程以及今后的延伸情况，进一步沟通概念之间的相互关系，激发学生的有意义学习，由被动接受转化为主动探究，这样学生对数学概念的掌握就“根深蒂固”。例如在学习三年级下册《小数的初步认识》这一课中，基于学生的原有知识基础是分数的初步认识，所以教师先利用米尺把1 米平均分成10份，如图：

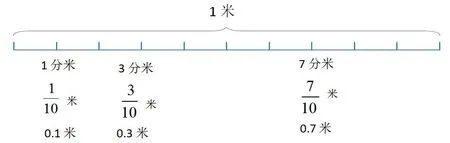
取其中的1 份就是也就是十分之一米，取其中的3 份是3 分米，也就是十分之三米，取其中的7 份是7 分米，也就是十分之七米。十分之一米可以写成0.1米，十分之三米可以写成0.3米，十分之七米可以写成0.7 米。由此让学生理解十分之几表示一位小数，一位小数就是十分之几。

二、借导图，“历”探究过程

《数学课程标准》对学生的学习情况及教学情况提出了新的要求，指出学生学习的过程需要充满个性化，需要是主动、生动活泼的。小学数学的学习方式不应局限于固定模式或填鸭式教学，教学方式应该是丰富多样的，自主探索、积极思考、合作交流、动手实践等均应是数学学习的常用途径。此外，在教学过程中应充分尊重学生是学习的主体这一原则，为学生提供充分的观察、思考、推理、计算、验证等空间与时间。我在教学平行四边形面积时，不是简单地把公式直接灌输给孩子，而是利用思维导图。

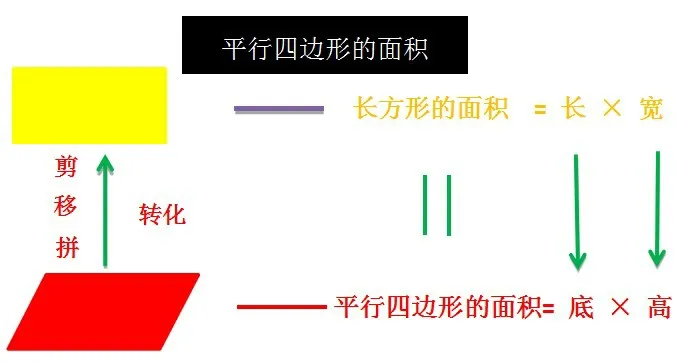
先引导学生把平行四边形沿着它的高剪下来，通过割、补后，可以将平行四边形转换为长方形，但两种图形具有相同的面积。基于此，引导学生对相关内容进行观察与思考，如长方形的长和四边形的底长度是相同的，长方形的宽度和平行四边形的高度是相等的。然后按照计算公式长与宽的乘积即为长方形的面积，推导出平行四边形的面积等于底乘高。这个思维过程让学生经历了剪、移、拼几个重要阶段，渗透了数学转化思想，这样让学生亲身经历新知识的形成过程，他们对平行四边形的面积公式就记得根深蒂固。

三、借导图，“现”思维方式。

纵观小学数学试卷，“解决问题”部分大约占百分之三十，所以解决问题的教学 不仅是小学数学教学的重要内容，还是教学的难点。特别是新教师或年轻教师 在教学时没有注重算理的教学，未能达到提高小学生的问题解决能力的目的。很多题目所出示的条件都是间接的，由于找不到解题思路，所以中等以下的学生解决问题部分失分严重。此时借助思维导图，可以帮助学生对数学信息进行深层加工，把握信息之间的联系，把隐藏在题目中的思维“暗线”鲜明地体现出来，形成一定的思维方式，提高学生解决问题的能力。

比如在教学“和倍问题”的过程中，有这样的一道题“果园里有梨树、桃树、苹果树，共有490 棵，梨树比桃树的2 倍多40 棵，苹果树比桃树的2 倍少50棵。梨树、桃树和苹果树各多少棵？”学生在解题的过程中，能找准1倍数是桃树，而“梨树比桃树的2倍多40棵，苹果树比桃树的2倍少50棵。”这个数学信息学生无法理解为“梨树要去掉40棵，才是桃树的2倍，苹果树要加上50棵才是桃树的2倍。”此时，教师如果使用思维导图（画线段图）的形式体现出来：

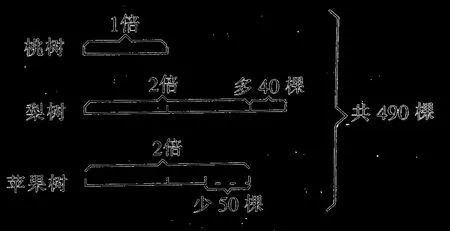
孩子就不难理解，多的先减，少的先加。总棵数就要相应减去40 棵（梨树）和加上50 棵（苹果树），就相当于桃树的1+2+2=5（倍），从而求出桃树的棵数。

四、借导图，“明”知识体系

数学知识表面上看起来星星点点，就像散落的珍珠，其实它们存在着千丝万缕的关系。而如何引导学生发现、掌握各个知识点间的关系，将相关知识点有效连接起来，形成系统的知识网络则是教学的重点与难点。因此，在教学过程中教师需要合理地对思维导图进行应用，协助学生了解、掌握知识间的关系及变化过程，逐渐形成清晰的知识体系，更好地对所学内容进行整体观察、回顾与分析，查漏补缺，从而达到节约时间、提高教学效率的效果。

比如，在复习四年级下册《小数的意义和性质》这一单元时，所涉及的知识点很多：有小数的意义、读法、写法、小数的性质和大小比较、小数点移动引起小数大小的变化、小数与单位换算、小数的近似数。如此零碎的知识让学生整理起来错综复杂，在执教这课时通过思维导图（智慧树）的形式把这些知识点有条理地体现出来，让学生形成系统的知识体系。

五、结语

总之，思维导图作为“教”的策略，能有效地改变学生的认知方式，切实提高教学效果；作为“学”的策略，能促进学生的自主性学习，培养学生的思维能力。在平时的教学中，我们要尽量合理地借助思维导图，成就课堂教学之高效。当然，思维导图的合理运用，需要我们去探索、去研究、去实践。只有这样，数学课堂才能在“思维导图”的点缀下越演越精彩，真正做到“数”海无涯“图”作舟。