从有理数到实数的历史演进

■山东省临沂市临沭县第二初级中学 袁玉晓

处于当今信息化、大数据时代，我们每天都会迎来铺天盖地的数据，数学更是无时无刻不在服务于人类社会。作为数学最基本元素的数，其是从现实生活中经过多年的实践而来，我们看不见摸不着这些美丽的小精灵，但超越了虚拟世界和物质世界的局限，拥有着无穷无尽的魅力。然而诸如数的本质是什么？如何定义无理数？有理数一样无理数多吗？实数是什么等问题，即使今天回答起来也并非易事。正如英国哲学家、数理逻辑学家罗素(B. Russell，1872-1970)曾说：“人类了解到两只羊中的2 和两天中的2 是同一个概念，竟花了几千年时间。”同样人类从认识自然数、有理数，再到实数也用了两千多年的时间。

一、《九章算术》中的无理数

人有10 个手指，计数时自然会以手指辅助。正是由此开始，人类祖先堆石子，数贝壳，刻痕计数，结绳计数等，直至创造文字、数字及算盘、筹算、计算器等计数用具。这一切皆源于手指计数基本法则，无疑其自然孕育形成了10 进制系统。此乃是人类千百年来积累的宝贵智慧财富。

大约在3000 多年前，中国古人就已形成了自然数概念，随后便掌握了自然数的运算法则。而在《九章算术》中，已对分数、正负数和无理数等概念均给出明确而完整的描述。在“少广”篇的开方术中写道，若开之不尽者为不可开，当以面命之。故同负数一样，中国古人对无理数的接纳显得非常从容和自然，且关于无理数的应用又是那样得心应手。在中国古代数学中，“面”常指平面图形的边，而这里则应是指正方形的一边。“以面命之”意指将开方不尽的数借助“面”来表示。

为了表示开方不尽的根数(无理数)，刘徽在《九章算术》注释中建立了小数概念。“不以面命之，加定法如前，求其微数(指小数部分)。微数无名者以为分子，其一退以十为母，其再退以百为母。退之弥下，其分弥细。”其大意就是用10 进小数来无限逼近无理数。这是一条完善实数系的正确道路，但因刘徽的数学思想远远超越了其时代，可惜未能引起后人的足够重视。

二、毕达哥拉斯学派发现无理数

“万物皆数”是古希腊毕达哥拉斯学派的基本信条。不过他们所说的“数”仅仅是指有理数。公元前500年左右，毕达哥拉斯学派主要成员之一希帕苏斯（Hippasus， 约公元前470）发现了一个惊人事实：边长为1 的正方形，其对角线长度不可公度(即不能用整数或整数之比来表示)。那这个数是什么，既不是整数，也非有理数。该发现很快引起了该学派的恐慌，认为其动摇了他们在学术界的统治地位。因毕达哥拉斯学派把抽象数作为万物本原，他们研究数之目的是试图通过揭示数的奥秘来探索宇宙永恒真理。“万物皆数”是毕达哥拉斯学派的一种信念，是其宗教、哲学和数学思想的基础。而无理数的发现彻底击碎了其基本信念，致使整个学派失去了赖以存在的基础。对毕达哥拉斯学派来说，整数是一切的基础，认为任何事物皆可由整数表示出来。但无理数的发现使整数的原子地位受到了质疑，这就是该学派乃至整个希腊数学最为恐惧的科学事实。

希帕苏斯第一次揭示了有理数系不能同连续直线同等看待，有理数并未布满数轴上的点，在数轴上存在不能用有理数表示的“孔隙”。而这种“孔隙”经后人证明简直多得“不可胜数”。故古希腊人把有理数视为连续衔接的算术连续统设想彻底破灭了。

不可公度的本质是什么？两个不可通约的比值也一直被认为是不可理喻之数。意大利画家达芬·奇（Leonardo di ser Piero da Vinci，1452-1519）称之“无理之数”，德国天文学家开普勒(J. Kepler， 1571-1630)称之“不可名状之数”等。后逐步定名为“无理数”。故我们今天所说的“无理数”并非“无理”，实为“不可通约”之意。

三、戴德金分割

直到文艺复兴时期，如何定义无理数仍在探索之中。数学家斯蒂费尔（Michael Stifel，1486-1567）曾使用各种无理数，甚至还用过这种在当时来说是新型的无理数。但他承认：“当我们想把它们数出来（用十进制小数的形式）时，却发现它们无止境地往远处跑，因而没有一个无理数实质上能被我们准确地掌握住。而本身缺乏准确性的东西，就不能称其为真正的数。故正如无穷大不是数一样，无理数也不是真正的数，而是隐藏在一种迷雾后面的东西。”

严密无理数定义直到1857 年才给出，第一个给出者是德国数学家魏尔斯特拉斯(Karl Weierstrass，1815-1897)。他先从自然数出发定义有理数，然后通过无穷多个有理数集合来定义实数。其定义不需引入新的数学对象作为无理数，而是承认10进制有限小数和无限循环小数是有理数，而10进制无限不循环小数则是无理数。在推理过程中，魏尔斯特拉斯最初只是将无理数看成一个纯粹记号，一个尚不清楚其意义的数学对象。后在10 进制小数全体集合内引入加法和乘法运算，并规定其中任何两个数之间的序，验证了其满足域公理、序公理、阿基米德公理和连续性公理。再经过多步逻辑推导，最终给出了严密的实数定义。

1872 年，戴德金(J.W.R.Dedekind，1831-1916)、康托尔(G. Cantor，1845-1918)、梅雷(Melay)和海涅(Heine)等数学家几乎同时发表了其各自的实数理论。其中戴德金从连续性要求出发，用有理数“分割”来定义无理数。

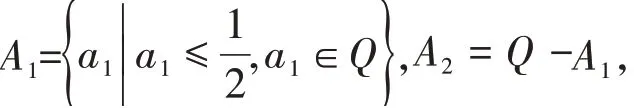
戴德金所应用方法被称之戴德金分割。他把有理数集Q 划分为两个非空且不相交子集A1和A2，并使对∀a1∈A1，∀a2∈A2，总有a1＜a2。一个实数a被定义成上述有理数的一个分割，即a=(A1，A2)。可见，有些分割是有理数产生，这时或A1有最大元素，或A2有最小元素。如：A1具有最大元素就称分割(A1，A2)定义了有理数但在这种情况下，同一个有理数会产生两个分割，即它可能是A1的最大元素，也可能是A2的最小元素，这时则认为这两个分割是相同的。而有些分割不是由有理数产生，这时A1和A2皆无最大或最小元素，此时则称分割(A1，A2)定义了一个无理数。例如，可知，在A1和A2中不存在最大和最小的元素，这样分割(A1，A2)就定义了无理数戴德金对无理数的定义，在数轴上可以被粗略地解释为，每个有理数根据其大小和正负都唯一地对应于数轴上的一个点，而无理数被定义在有理数所形成的“空隙”中。如此，戴德金就把实数集R定义为有理数集Q的一切分割。

康托尔则在不假定无理数存在的条件下，通过“基本级数”引入了无理数。他不仅给出了无理数理论较为详细的论述，还引进了实数理论，明确指出实数既包含有理数又包含无理数。同时康托尔还定义了实数的四则运算和两个实数的不等关系，进而得出了著名的戴德金-康托公理：直线上任意一点皆与实数一一对应。

任何科学发展皆非一帆风顺，而是在奋斗中一步步砥砺前行。从无理数的发现至给出其严格定义历经了两千余年筚路蓝缕之程，其所引发的第一次数学危机对数学科学的发展产生了极为深远的科学影响，促使人们从依靠直觉、经验而转向逻辑证明，推动了公理化体系的发展，孕育了微积分思想，进而产生了现代数学。