一道几何题的拓展与延伸

陕西省西安市第八中学(710001) 王公民

思维是数学之体操,尤其解几何题,对已知条件的拓展、延伸,得出不同的结论,变中有不变,不变中有变,继承发展,多姿多彩,深刻的反映了几何图形的本质属性,以一道几何题的探究为例.

原题已知等腰Rt△ABC 中,∠ACB = 90°,EF 是过点C 的直线,AE⊥EF,BF⊥EF 垂足分别为E、F,试问线段EF 与AE、BF 之间有什么等量关系? 为什么?

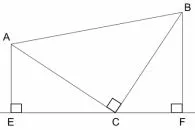
图1

答: EF =AE+BF.

理 由: 因 为∠ACB = 90°, ∠ECF = 180°, 所 以∠BCF + ∠ACE = 90°.因 为∠AEC = 90°, 所 以∠EAC +∠ACE = 90°, 所以∠EAC = ∠BCF.因为在△AEC 和△CFB 中, ∠AEC = ∠CFB = 90°, ∠EAC =∠BCF, AC = BC, 所以△AEC△CFB (AAS), 所以AE =CF,EC =BF,所以EF =EC+CF =AE+BF,即EF =AE+BF.

拓展1直线EF 过点C 旋转变形.

(1)原题中的直线EF 过点C 改为“直线EF 过点C,且绕点C 逆时针旋转,使0°＜∠BCF ＜45°其它条件不变,如图2,试问线段EF 与AE、BF 有什等量关系? 为什么?

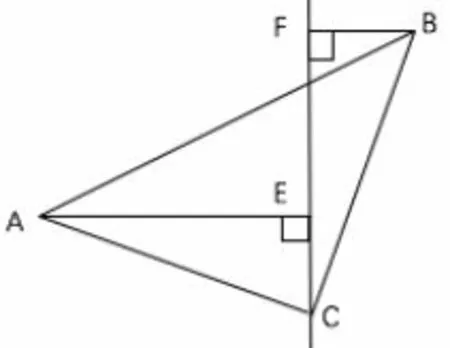
图2

答: EF =AE-BF.

(2)原题中的直线EF 过点C,改为“直线EF 过点C,且绕点C 逆时针旋转,使45°＜∠FCB ＜90°”,其它条件不变,试问线段EF 与AE、BF 有什么等量关系? 为什么?

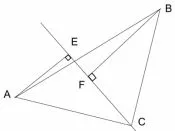
图3

答: EF =BF -AE.

理由同(1)略.

(3)原题中的直线EF 过点C 改为“直线EF 过点C,且绕点C 逆时针旋转,使∠FCB = 45°”,其它条件不变,如图4,则易见点E、F 重合,这时EF =0,AE =BF.

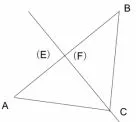
图4

拓展2△ABC 的形状发生变化.

(1)原题可改为“在等边△ABC 中, 直线EF 过点C,∠AEC = ∠CFB = 60°,如图5,试问线段EF 与AE、BF还有EF =AE+BF 等量关系吗? 为什么?

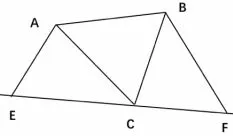
图5

答: EF =AE+BF.

理由: 因为△ABC 是等边三角形, 所以AC =BC,ACB = 60°.因为∠ECF = 180°, 所以∠BCF +∠ACE = 120°.因为∠AEC = 60°, 所以∠EAC +∠ACE =120°,所以∠EAC =∠BCF.因为在△AEC 和△CFB 中, ∠AEC =∠CFB, ∠EAC = ∠BCF, AC = BC, 所以△AEC ￤△CFB (AAS), 所以EC = BF, AE = CF, 所以EF =EC +CF =AE+BF,即: EF =AE+BF.

(2)原题可改为“在△ABC 中, AC = BC, 直线EF过点C, 且∠AEC = ∠CFB = ∠ACB, 如图6, 试问EF =AE+BF 仍成立吗? 为什么?

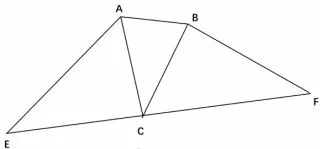
图6

答: EF =AE+BF.

理由: 因为∠ECF = 180°, 所以∠BCF = 180°-(∠ACE + ∠ACB).因为∠EAC = 180°- (∠ACE +∠AEC), 因为∠AEC = ∠ACB, 所以∠EAC = ∠BCF.因为在△AEC 和△CFB 中,∠AEC = ∠CFB,∠EAC =∠BCF, AC = BC, 所以△AEC△CFB(AAS), 所以AE =CF,EC =BF,所以EF =EC+CF =AE+BF,即: EF =AE =BF.(3)原题仅改为“直线EF 过△ABC 的顶点C, 且∠AEC =∠CFB =∠ACB.如图7 求证:

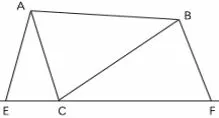
图7

证明: 因为相同图6, 易证∠EAC = ∠BCF.又因为∠AEC = ∠CFB,所以△AEC ∽△CFB,则成立,特别地,若则△AEC△CFB 这时与图6 是相同问题.