旋转-冲击凿岩系统钎杆最优转速控制特性研究

吕闯，徐赛华，高波，杜标

(1.长沙矿冶研究院有限责任公司，湖南 长沙410012；2.深海矿产资源开发利用技术国家重点实验室，湖南 长沙410012；3.浙江开山重工股份有限公司，浙江 衢州324002)

1 概述

在利用液压凿岩机等设备进行旋转-冲击钻进过程中，钎杆转速是反映钻进过程是否正常和考查钻进速度的重要参数，转速过快和过慢均表明钻进过程未达到理想的状态，操作者经常根据自身经验对推力进行实时调整，以求达到最理想的转速效果，但实际上由于各种工况的差异性，往往不能达到预期的效果。现如今，国外某些技术先进的凿岩钻车上已经配备了钻速自动控制系统，能自动检测液压凿岩机的钻孔速度，然后进行工作参数的反馈调节，实现最优钻速，我国凿岩钻车领域在这一块几乎还是空白。

2 最优转速控制系统

最优转速控制就是对钎杆转速进行闭环控制，其原理是利用转速传感器对钎杆转速进行检测，将其信号进行反馈，并和推进系统中比例溢流阀的压力信号进行比较，控制推进力，保持其最佳转速，其控制简图如图1所示。

图1 为一典型闭环控制系统，由其各环节传递函数构成的系统控制框图如图2所示。

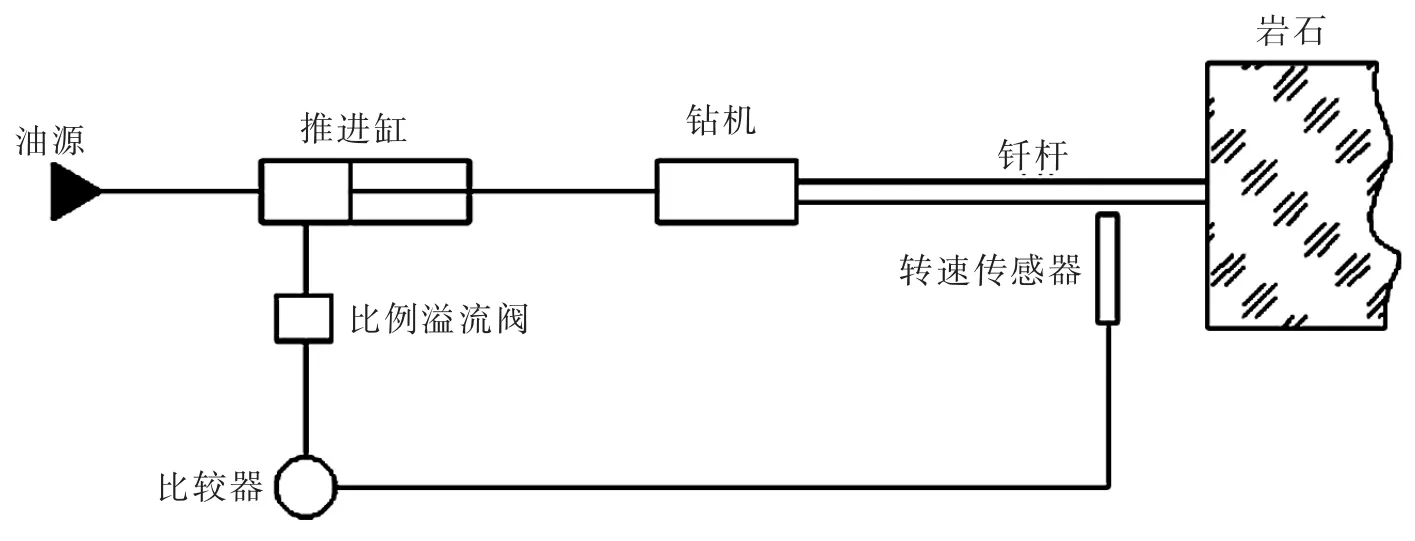
图1 控制简图

图2 系统控制框图

图2 中，F（S）：输入，推进机构工作压力输入信号

ε（S）：偏差信号

P（S）：钎杆旋转系统的传递函数

R（S）：微分环节

θ＇（S）：输出，钎杆转速信号

Q（S）：反馈回路传递函数

B（S）：反馈信号

系统的开环传递函数

系统的闭环传递函数

取反馈系统传递函数Q（S）=1，则系统为单位反馈系统，其闭环传递函数

3 系统动力学方程和频响函数

钎杆旋转动力系统可简化为图3 中的模型。

图3 钎杆旋转动力系统模型

旋转机构的转动惯量为J，输入的动力扭矩为M，钎杆的扭矩刚度与粘性阻尼系数分别为k和c，以钎杆转角θ作为输出，系统的动力学方程为

得到传递函数

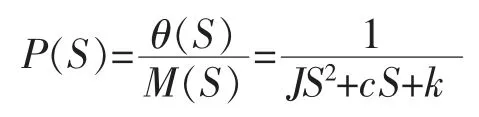
或写成

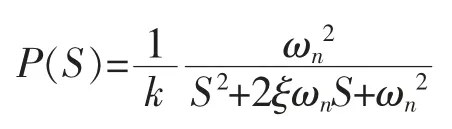
用（jω）取代S，则其频响函数

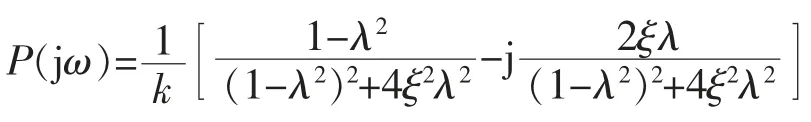
故其幅频特性

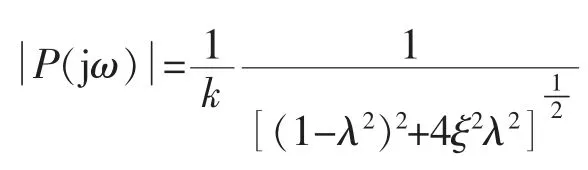
取ξ=0.5，当ω从0→∞（即λ由0→∞时），幅值由1 经极值点1.155 趋于0，相位由0°→180°，如图4所示。

图4 系统的幅值和相频特性

4 微分环节的传递函数和频响函数

框图中R（S）为微分环节，输出反映输入的微分，其传递函数

式中 T——微分环节的时间常数

5 控制系统的频响特性

5.1 系统的频响特性

由系统的传递函数，其频响特性可对应写为

开环:G（jω）=P（jω）·R（jω）·Q（jω）

5.2 系统开环特性的确定

由系统开环特性得到

5.3 系统闭环特性的确定

（1）求以Gk（jω）为前向通道传递函数的单位反馈系统特性

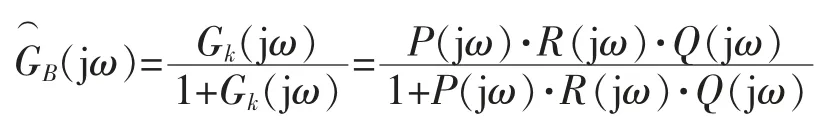
其分母

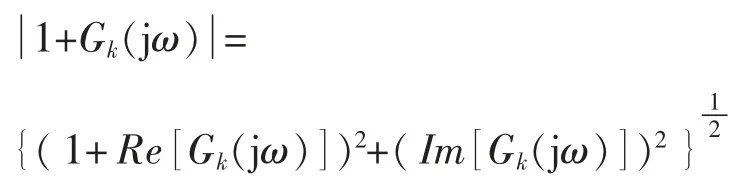
则

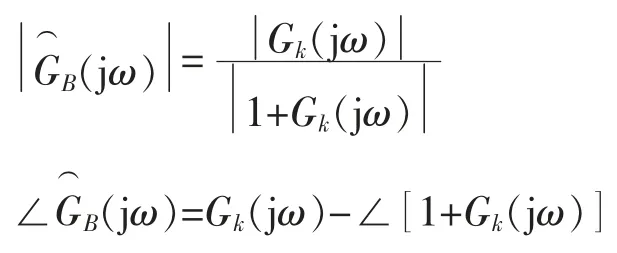
由此得出系统的闭环特性：

在Q（jω）为1 时，

GB（jω）＝，即为单位反馈系统特性。

5.4 频响特性计算

将GB（jω）写为

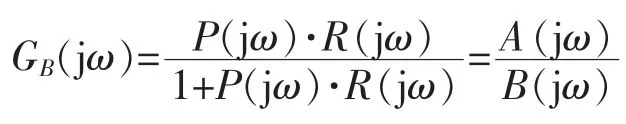
式中

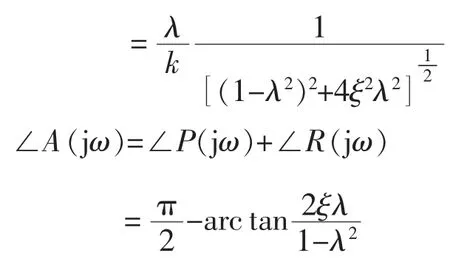
其实部

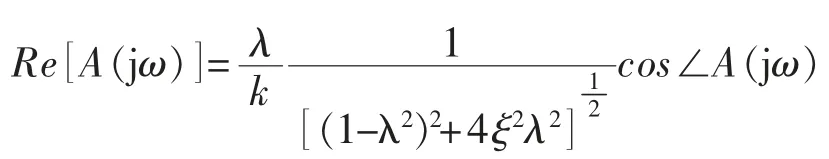
其虚部

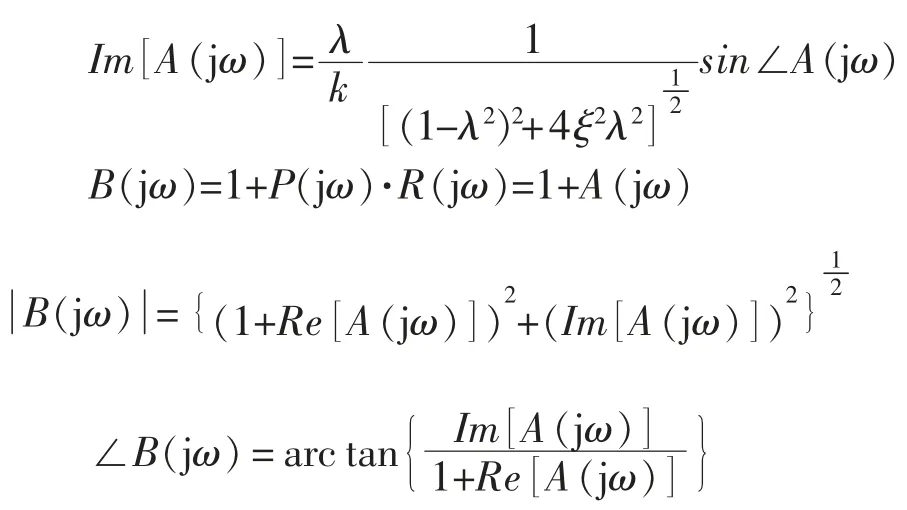
则系统闭环特性

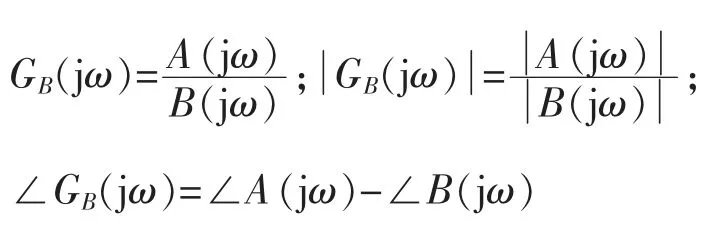
取ξ=0.5，k=1，根据P（jω），R（jω）频响特性，依上述方法计算，得到对应于不同λ 值向量特性（见表1所示）。

根据表1，可绘制控制系统的闭环频响特性（见图5所示）。

频响特性表明：

（1）在λ 值很小（ω→0）和很大（ω→∞）的情况下，系统的输出幅值均会很小。λ 值很小相应于钎杆转速值很低的情况；λ 值很大相应于钎杆转速值很快的情况，由于钎杆旋转系统的惯性，系统难于作出反应。

（2）在λ 趋于1，ω→ωn，即钎杆转动频率（转速）接近系统固有频率的情况下，系统具有最大的输出，由于实际钎杆转速信号远高于系统固有频率，故直接利用转速信号，不能使系统得到有效的反应。

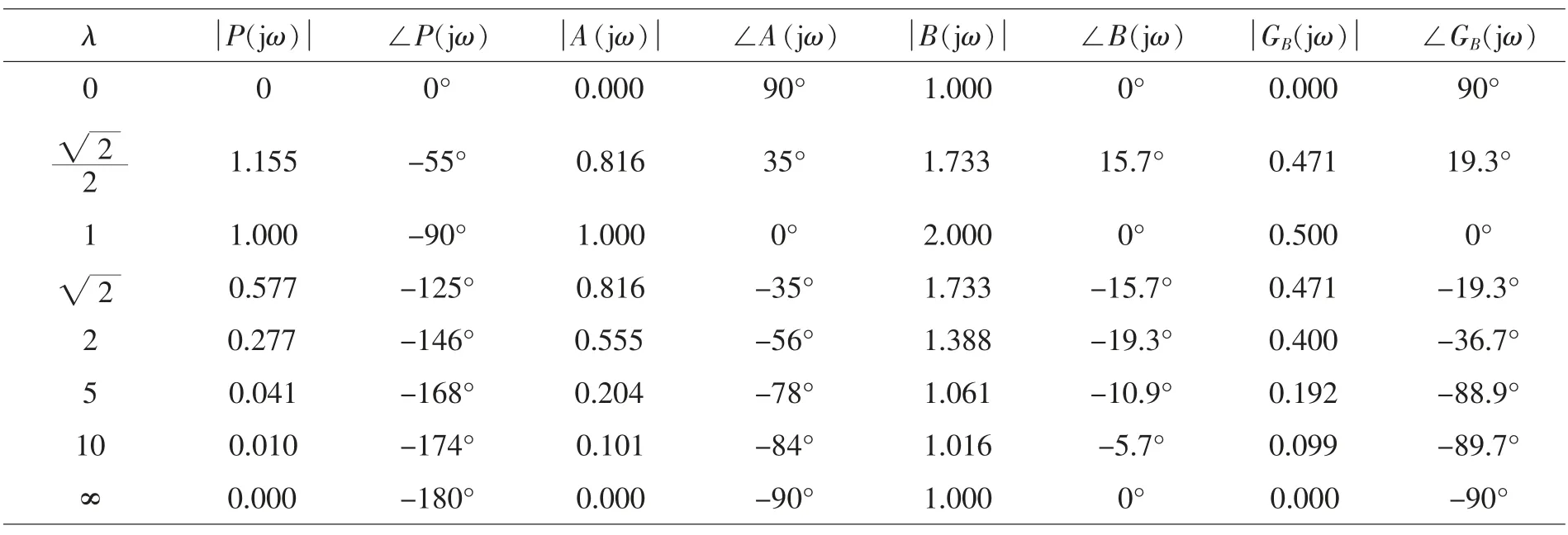
表1 对应于不同值的向量特性

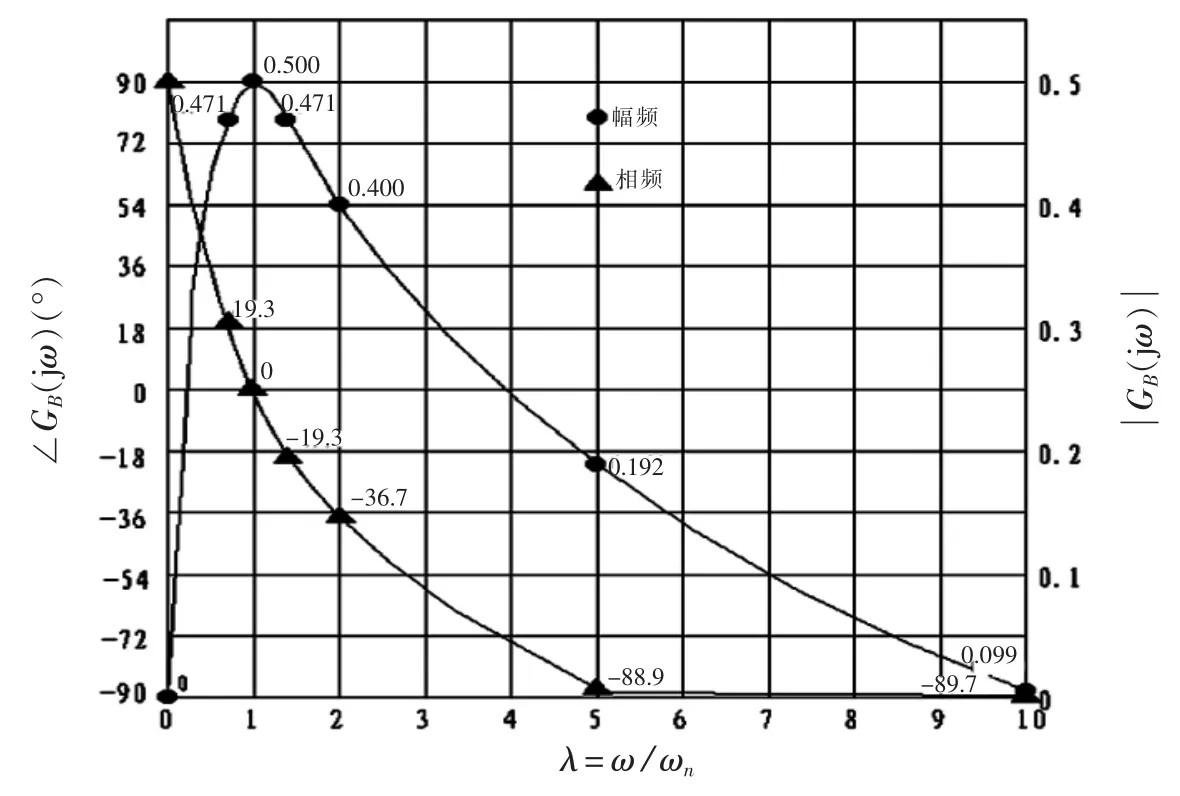
图5 控制系统的闭环频响特性

（3）系统的相移在-90°～90°之间变化，λ＜1，相移为正值；λ＞1，相移为负值。在一般情况下（λ＞1），输出时滞后输入∠GB（jω）。

（4）为了使系统得到有效的输出（反应）幅值，可采用以下方法：尽量加大微分环节的时间常数，即加长转速的取样时间，使之接近系统的固有频率。对输入高频信号进行数字预处理，分段取N个高频信号的均值作为输入，使其频率降低为ω/N°。

6 结语

旋转-冲击凿岩系统最优钎杆转速控制系统即是对钎杆转速进行闭环控制，其原理是利用转速传感器对钎杆转速进行检测，将其信号进行反馈，并和推进系统中比例溢流阀的压力信号进行比较，控制推进力，保持其最佳转速。文中所作的详细的理论分析，对建立最优转速控制系统具有理论借鉴价值。