基于ANSYS的潜孔冲击器活塞长径比优化仿真

何小宏

(山东天瑞重工有限公司，山东 潍坊 261000)

高气压潜孔冲击器以压缩空气作动力，在使用过程中将压缩空气转化为机械能，从而达到清洗孔底、冷却钻头以及产生钻进的目的。因其采用回转和冲击联合作用，具有质量好、成本低以及效率高的特点。活塞作为冲击器的主要工作部件，其结构的合理性直接影响冲击器的钻进效率。近年来，张国忠、戚靖洋等，围绕活塞的动力过程，采用点变换的方式建立结构参数与工作参数的相关关系[1]；曾璟等根据冲击器活塞载荷以及破损情况，提出一些提高活塞寿命的解决方案[2]；朱丽红、博坤等从潜孔锤活塞的结构以及材料两方面进行分析，利用相关模拟软件对改进活塞进行应力分析[3]。本文以某公司的5 寸高气压气动冲击器为研究对象，建立活塞撞击钻头的模型，从而研究活塞质量一定，活塞长度发生变化时的应力变化。

1 活塞撞击钻头的工作原理

图1 中，活塞受到前气室压缩空气的作用进行回程运动，回程运动完成后，后气室充满的压缩空气推动活塞进行冲程，活塞以一定的速度撞击钻头尾部，将能量传递到钻头。钻头前部合金齿与岩石接触，传递压力至岩石，岩石被挤压产生裂纹。钻头在钻机带动下旋转，旋转中有裂纹的岩石被切削下来。

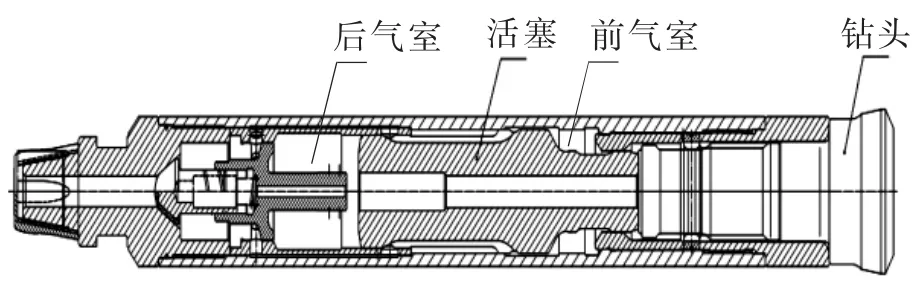
图1 冲击器剖面图

高气压冲击器的活塞撞击钻头瞬间，活塞的运动速度(大小和方向)发生急剧变化，在大小和方向都随时间作周期性变化的动载荷作用下，活塞的应变不是整体均匀的应变，质点的运动速度也不是整体一致的速度，应变和速度都以应力波的形式传播。在冲击回转钻进过程中，冲击器利用活塞的撞击，将能量通过钻头传递到孔底岩石，实现碎岩钻进。潜孔锤的活塞采用了变截面结构，应力波在其中传播时，在截面变化处必然会发生透射和反射。等截面受到的应力是压应力，而变截面受到的就不单是压应力，还有拉应力。

2 活塞撞击钻头的能量传递理论分析[8]

2.1 冲击器凿入分析

活塞撞击钻头，由于本身变形很小，可以把活塞看成刚体，将活塞、钻头整个系统分成n个小段。

2.1.1 应力波叠加原理

冲击器活塞工作时撞击钻头产生的应力波作用在钻头前段，此时

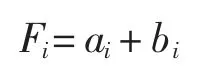
式中 Fi——活塞所受总力，N

ai——顺波

bi——逆波

2.1.2 截面积发生改变处应力波的传播

在截面发生变化处应力波会产生入射波及反射波，其传递到接触面时，接触面所受力为

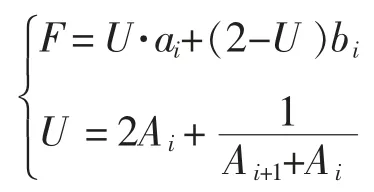
式中 F——接触面受到的总力，N

U——透射系数

Ai+1——活塞截面积，m2

Ai——钻头截面积，m2

2.1.3 活塞与钻头撞击面上的应力波传播

由于撞击面所受力为非线性，可知撞击面上总受力为

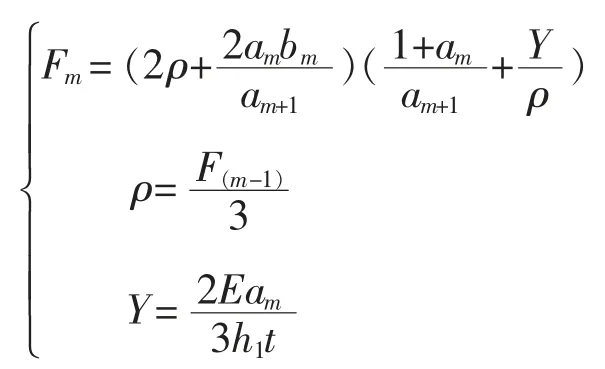
式中 Fm——撞击面所受总力，N

am——顺波，N

bm——逆波，N

am+1——m+1 顺波

Y——弹性模量，N/m2

h1——撞击面局部变形系数，N2/3/m

t——时间步长，s

ρ——材料密度，kg/m3

F（m-1）——m-1 次撞击时所受的力，N

E——弹性模量，MPa

2.1.4 活塞撞击反射

在撞击端，顺波是已知条件，根据活塞撞击钻头的边界条件可知逆波为

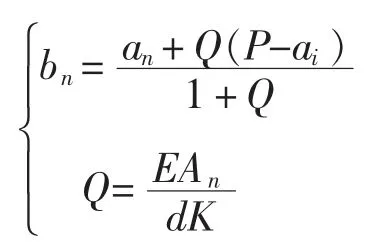
式中 bn——逆波，N

P——活塞撞击力，N

Q——无因次量

an——顺波，N

An——活塞截面积，m2

d——差分步长

K——凿入系数

2.1.5 凿入效率

凿入效率为钻头破碎岩石所做功与活塞撞击动能之比，即

式中 Δ——凿岩效率

M——活塞的质量，kg

F——最大凿入力，N

v——活塞的冲击速度，m/s

3 有限元仿真分析

3.1 改进的方案

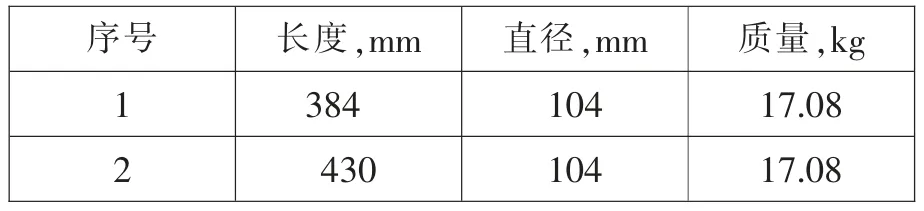
表1 活塞改进方案

改进后，冲击器整体加长，配气参数不做改变，即保证活塞的冲击行程不变。活塞直径相同，长度不同，可通过改进结构，保证活塞的质量相同。

根据凿岩效率理论，活塞长度与活塞直径之比在3～4 之间时[4]，能量传递效率最高。因此，本文在不改变活塞质量的前提下，采取的方案1 活塞长度与直径之比设为3.69，方案2 活塞长度与直径之比设为4.13。

图2 活塞撞击钻头示意图

3.2 三维模型的建立

由于整个冲击器结构复杂，本文只针对潜孔冲击器活塞进行模型建立，以山东天瑞重工公司生产的TRC55 型高气压潜孔冲击器活塞以及配套钻头为实验模型，运用Pro/engineer 三维软件对活塞、钻头以及岩石的三维模型绘制。

3.3 定义材料属性以及单元类型

活塞材料采用20Ni4Mo，其材料密度为7.8×103kg/m3，杨氏模量218 MPa，泊松比为0.3，材料定义为分段线性塑性材料[5,6]，钻头主体采用23CrNi3Mo,材料密度为7.88×103kg/m3，杨氏模量358 MPa，泊松比为0.35。岩石选用大理石，密度为2.68×103kg/m3，剪切模量26.8 MPa，塑性硬化模量46.7MPa，体积模量为16 MPa，破裂应力150MPa，定义为一种弹性应变失效模型。

活塞、钻头以及岩石的单元类型均定义为8节点3D SOILD164 单元。

3.4 网格划分

活塞两端以及主体倒角处网格采用手动划分，划分为六面体网格，其他位置使用网格自动划分方法。

钻头主体与活塞划分方法相似，倒角处采用手动网格划分，其他采用网格自动划分。合金齿由于具有复杂的结构以及在凿岩过程中与岩石处于高速摩擦，需要细分网格，采用手动线节点数网格划分方法进行划分，一共划分为224960个。

岩石性状规则，直接采用自动网格划分，划分成规整的长方形六面体结构，共划分为100000个。

图3 活塞、钻头与岩石的网格划分图

3.5 接触界面的定义与控制

为了能充分描述撞击凿岩过程中活塞与钻头、钻头与岩石之间的相互作用，需要定义相互之间的接触类型，活塞前部与钻头尾部之间的接触定义为面对面自动接触（ASTS），即*Contact_Automatic_Surface_To_Surface。钻头合金齿与岩石之间的接触定义为侵蚀接触（ESTS），即*Contact_Eroding_Surface_To_Surface，同时控制活塞为静态模型，钻头为动态模型。

3.6 施加载荷以及约束

载荷以及约束的施加对整个仿真至关重要。为了能尽可能客观地反应真实工作状况，定义岩石为无限大，但是截取其中0.16×0.2×0.05 m的大小，并将模型5个面（与合金齿接触面除外）定义为全约束的无限无反射边界条件，从而模拟岩石的无限大。

钻头在工作时处于旋转状态，根据现场配套钻机的实际工况，确定钻头的转速[7]为40 r/min，冲击器配套钻机钻压一般为500～1000 N/cm 钻头直径，在这里设为700 N/cm，钻头的直径为135 mm，因此钻压为9450 N。

活塞冲击功、冲击频率以及活塞冲击速度根据matlab 冲击仿真计算得到，活塞在距离钻头1 mm 处时速度为10.018m/s，冲击功为857 J，冲击频率为26 Hz。

4 仿真结果与分析

4.1 活塞与钻头的动能传递

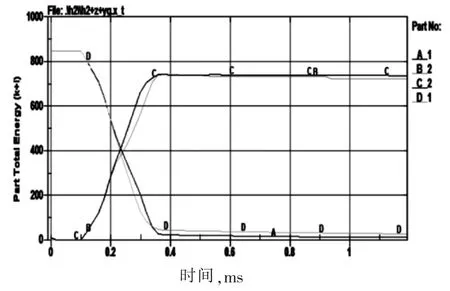
图4 活塞与钻头的动能传递图

图4 中曲线C（钻头）、D（活塞）分别表示方案1 钻头和活塞在整个冲击运动过程中内部能量变化，曲线A（活塞）、B（钻头）分别表示方案2活塞和钻头在整个冲击运动过程中的内部能量变化，在0～0.15 ms 时，活塞与钻头处于分离状态，方案1、方案2 活塞动能都保持在857 J，钻头的动能始终为0 J，0.15～0.25 ms 时活塞与钻头开始接触，活塞的动能减小，钻头的动能开始增大，此时钻头开始凿岩，在0.25 ms 时活塞与钻头的动能趋于稳定，钻头继续破碎岩石，活塞则开始与钻头分离，做回程运动，整个撞击过程中活塞与钻头动能趋于稳定时，方案1 动能分别为30 J与720 J，活塞获得的最大动能830 J，方案2 动能分别为50 J 与720 J，活塞获得的最大动能800 J，据此算出方案1 活塞撞击钻头的能量转换效率为86.7%,方案2 活塞撞击钻头的能量转换效率为90%，能量传递效率提高3.3%。

4.2 活塞与钻头应力波传递分析

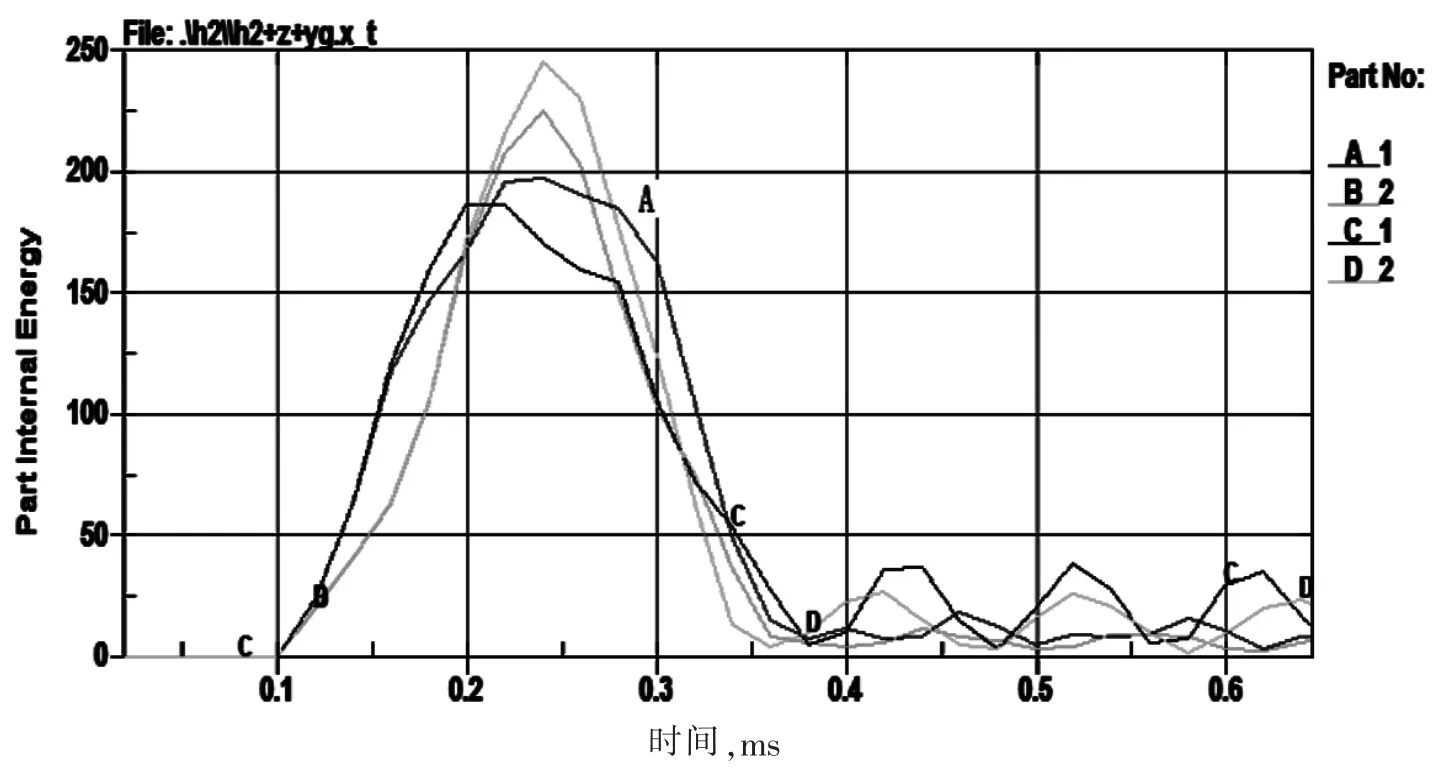
图5 活塞与钻头应力波传递图

图5 是活塞与钻头应力波传递曲线图，其中A、B 是方案1的活塞与钻头中应力波传递曲线，C、D是方案2 活塞与钻头应力波传递曲线，从图中可以看出，方案2 钻头中应力波传递时间长于方案1，有利于增加单次钻头凿岩时间，提高凿岩效率。同时，方案1的活塞中应力波峰值明显高于方案2活塞中应力波传递波峰值，因此，方案2 活塞长，应力波交替循环的相对次数就减少，这样活塞的疲劳程度就会改善，从而延长活塞使用寿命[4]。

5 结论

（1）活塞长径比由3.69 变为4.13，冲击器凿岩效率提高3.3%，可以通过改变活塞长径比，增加活塞长度来提高冲击器的工作效率。

（2）通过仿真分析发现，冲击器活塞越细长，应力波持续时间越长，振幅越低，有利于破碎岩石以及提高活塞与钻头的寿命。