重力梯度欧拉反褶积及其在文顿盐丘的应用

侯振隆 王恩德 周文纳 吴国超

(①东北大学深部金属矿山安全开采教育部重点实验室，辽宁沈阳 110819； ②东北大学资源与土木工程学院，辽宁沈阳 110819； ③兰州大学地质科学与矿产资源学院，甘肃兰州 730000； ④浙江大学地球科学学院，浙江杭州 310058)

0 引言

重力勘探是重要的物探方法之一，观测数据可用于地下空间物性分布[1]和场源位置[2]的计算。欧拉反褶积(Euler Deconvolution,ED)[3]是一种重磁勘探数据处理方法，可以计算地质体的埋深、位置等参数，被广泛应用于各类资源勘查工作中。相比于传统重力异常数据，重力梯度数据精度较高，信噪比也更高，包含更多的地质信息，在对地质体的边界[4]、形状识别[5]上有较好的应用效果。Zhang等[6]提出利用重力全张量梯度数据进行欧拉反褶积，能够更充分利用梯度数据。针对传统欧拉反褶积中反演结果多解性强和空间分辨率较低等问题，一些学者进行方法改进，包括引入基于水平梯度率[7]、均衡边界检测滤波器[8]、梯度反褶积[9]、垂向一阶导数[10]和解析信号比值[11]等；联合不同高度观测面上数据的欧拉反褶积，也被应用于实际勘探中[12-13]。以上研究均一定程度上改善了欧拉反褶积的计算效果。

本文在传统方法基础上提出重力梯度数据联合的欧拉反褶积(Joint Euler Deconvolution of Gravity Gradiometry Data,JEDGG)法，通过计算垂向导数重新推导了反演方程，联合多个梯度分量建立了新的方程组，避免了构造指数的选择以及不同分量间的换算。模型试验验证了该方法的有效性，并将其应用于文顿盐丘地区的实测重力数据，在盖岩东部发现了一处小型构造，进一步探明了该区地下地质结构。

1 重力梯度联合欧拉反褶积原理

根据欧拉齐次方程的定义[3]，传统欧拉反褶积公式为

=N(B-f)

(1)

式中： (x,y,z)和(x0,y0,z0)分别代表观测点和地质体中心坐标， 其中z0表示异常体中心深度；f和B分别表示观测异常场和背景场；N为构造指数，如薄板的N取0.5，而球体取2.0。将上式转化为向量积的形式

(2)

用引力位V在x、y和z三个方向的一阶导数分别替代式(1)中的f，有

(3)

由于实际数据中缺少Vx和Vy，只能通过分量转换得到，故式(3)不适于高精度重力梯度数据的计算。对式(3)两端分别计算z方向上的导数，可得

(4)

整理式(4)，合并同类项，将三阶导数转化为计算二阶导数的一阶偏导数

(5)

式中Vxz、Vyz和Vzz为重力梯度数据，计算其导数后利用式(5)可求解地质体坐标。需要注意的是，理论上计算z方向导数不会对结果造成影响，但计算实际数据时，求导数相当于滤波，将会放大噪声。因此，本文将二阶导数的一阶垂向偏导数转化为一阶导数的二阶偏导数。由于引力位满足拉普拉斯方程，将式(5)中引力位在z方向的三阶偏导数转化为

(6)

将式(6)代入式(5)，转化为矩阵形式

(7)

由式(7)可知，本文方法避免了构造指数的选择以及计算垂向导数引起的误差，计算形式更简单。联合Vxz、Vyz和Vzz，减少了分量转换步骤。与传统方法一样，梯度联合欧拉反褶积也需要使用滑动窗口，窗口中所有测点的方程构成方程组。

2 模型测试

为测试方法的有效性，在笛卡尔坐标系下建立理论模型并进行试验。试验包含不加噪声、加入5%高斯噪声两种情况，并对比传统ED方法的结果。试验中长方体密度均设为1.0g/cm3。根据式(2)和式(7)，可分别计算ED和JEDGG的结果。

2.1 单长方体模型

首先设地下一长方体的顶面埋深为100m，三维尺寸为800m×800m×200m，观测点距为20m，异常体水平位置及理论异常见图1。滑动窗口的大小为19×19，即窗口内包含19×19个测点。试验结果见图2～图5。

从图2、图3可以看出，在无噪数据试验中，JEDGG结果与理论模型基本一致，长方体的水平边界被清晰地显示，三维结果可较准确地揭示长方体的埋深；相对地，ED结果的聚焦程度低于JEDGG，其反映的目标体的水平和深度方向上的范围均比真实值大，并且水平方向上边界不连续，仅能反映异常体顶点的位置。在含高斯噪声数据试验中，其结果(图4、图5)与无噪数据计算结果(图2、图3)相似，说明JEDGG适用于含噪声数据的反演。

2.2 双长方体模型

为了验证方法对不同埋深地质体模型的计算效果,建立一个双异常体模型进行试验。设地下有两个完全相同的长方体，大小均为500m×500m×100m，顶面埋深分别为100m和200m，观测点距为20m，这两个异常体的平面位置及理论重力梯度异常场见图6。如果JEDGG能够同时准确地反演出这两个长方体的空间位置，则验证了方法的有效性。计算中滑动窗口大小设为11×11，对该模型分别应用JEDGG和ED方法计算，结果见图7～图10。

图1 单长方体模型产生的理论重力梯度异常场(上)及含5%高斯噪声的重力梯度异常场(下)

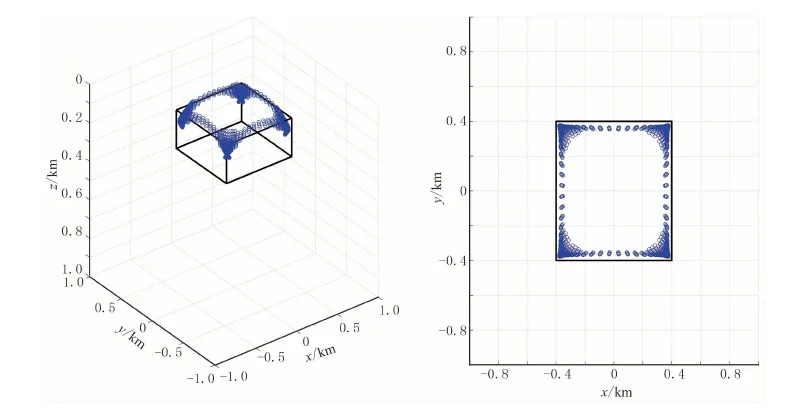
图2 单长方体模型正演数据(无噪声)的JEDGG结果

图3 单长方体模型正演数据(无噪声)的ED结果

图4 单长方体模型正演(含噪声)的JEDGG结果

图5 单长方体模型(含噪声)的ED结果

图6 双长方体模型产生的理论重力梯度异常场(上)及含5%高斯噪声的重力梯度异常场(下)

图7 双长方体模型正演数据(无噪声)的JEDGG结果

从图7和8可见，JEDGG法能够同时反演得到两个长方体的水平位置和埋深，其中深部长方体的范围比真实值略小。与ED法计算结果相比，JEDGG计算结果的空间分辨率更高，ED反演得到的异常体范围偏大、边界不连续。对于含噪声(图9、图10)情况，JEDGG法计算结果与理论值基本一致，仅在顶面顶点处出现了些许虚假解，即顶点的上方出现“发散状”的解，但不影响对长方体位置的判断； ED计算虽然没有这样的解，但是长方体范围仍偏大。这个试验也验证了JEDGG处理含噪数据的有效性。

理论数据和含噪数据试验结果都证明了JEDGG反演效果优于ED，结果更准确，且更适用于较复杂的地质情况。

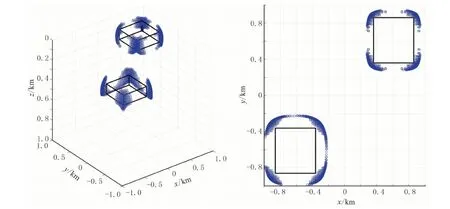
图8 双长方体模型正演数据(无噪声)的ED结果

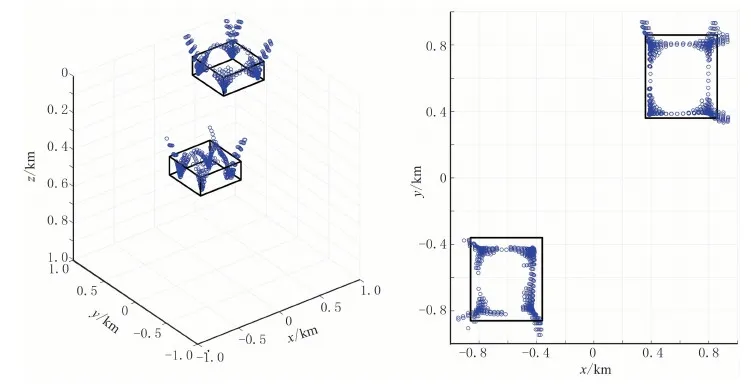
图9 双长方体模型正演数据(含噪声)的JEDGG结果

图10 双长方体模型正演数据(含噪声)的ED结果

3 应用实例

基于上述对JEDGG方法的理论研究与模型试验，将其应用于文顿盐丘的实测重力全张量梯度数据。文顿盐丘位于美国路易斯安那州西南，由于富含油气资源而成为研究热点。文顿盐丘包含岩盐和上方的盖岩，实测异常主要来源于盖岩[14-16]。根据Ennen等[15]和Oliveria等[16]的研究，盖岩埋深约为160～650m。实测数据的x和y轴的正方向分别代表东、北。数据已经密度为2.2g/cm3的地形改正和低通滤波，选取Vxz、Vyz和Vzz三个分量进行JEDGG计算，结果见图11。

从图11可以判断盖岩顶的水平范围，并与其他学者对该盖岩的研究结果[17-19]对比，发现基本吻合。还可以看出，盖岩的埋深在西部较小，约为125m，较深的位置出现在南部，约550m；顶部深度由东南分别向南部、东部增加，而盖岩两端的深度在减少，使盖岩形态在空间上呈弯曲的“W”形状。根据已有的密度分布资料[16-20]可知，盖岩的密度高值位于东南方向，即图11c中东西方向442.5～443.0km、深度方向275～425m的区域，以及图11d中南北向3334.0～3334.5km、深度250～550m的区域。结果表明JEDGG法对高密度区域反演效果较好。一般将剩余密度大于0.15g/cm3的区域解释为盖岩。从反演结果可见，JEDGG可以反演出剩余密度为0～0.15g/cm3的异常，即盖岩外围部分，盖岩呈“南高北低”、“东高西低”的形态。因此，JEDGG反演结果进一步完善了盖岩位置的解释结果。

另外，在图11中可见，盖岩的东部可见一处小规模的、呈块状的解，常规密度反演[16-20]中没有该显示，初步认为这是一处低剩余密度、块状或脉状的异常体的顶端。另外，在埋深0～150m范围内还存在少量零星分布的解，分析认为是结果中的干扰成分，不具实际意义。

从图11d可见，在南北方向3334km处、深度范围0～100m的区域为盖岩西部解的投影，不能解释为盖岩整体深度范围。

综上所述，利用JEDGG反演结果可以判断文顿盐丘地下盖岩的水平范围：东西方向441.7～442.9km， 南北方向3333.8～3334.8km， 深度125～550m。

盖岩东部还存在一小型构造，有待在以后的勘探工作中做进一步详查。

图11 文顿盐丘实测重力梯度数据JEDGG反演结果

4 结束语

本文提出了多分量重力梯度数据的欧拉反褶积方法，该方法避免了构造指数的选择和分量转换，充分利用了梯度数据的高精度特点，提高了地质体空间位置的反演精度。模型数据试验证明了该方法能够较准确地识别模型位置。将该方法应用于文顿盐丘的实际数据，圈定了盖岩的范围并发现盖岩东部还存在一小规模的地质体，丰富了该区域的地下构造信息。

感谢Bell Geospace Inc提供的实测重力全张量梯度数据。