HTI介质方位观测PP波反射系数一阶扰动近似

单俊臻 吴国忱*② 龚诚诚

(①中国石油大学(华东)地球科学与技术学院，山东青岛 266580； ②海洋国家实验室海洋矿产资源评价与探测技术功能实验室，山东青岛 266580)

0 引言

反射系数公式定量描述了地震反射波振幅与介质弹性参数随炮检距、方位角的变化特征，是研究地震波正演与反演的理论基础。在均匀各向同性地层中，地震振幅具有随炮检距变化的特征，当地震波传播到弹性分界面处时，会产生纵横波反射与透射现象。Zoeppritz等[1]对各向同性弹性分界面处的纵横波反射、透射系数进行了定量表征；Aki等[2]基于Zoeppritz方程推导了基于纵横波速度、密度的纵波反射系数近似公式，更为直观地描述了弹性分界面处的介质参数差异与地震反射波振幅的关系。

随着油气勘探领域的不断发展，非常规油气藏的勘探与开发在油气勘探领域具有重要意义。裂缝具有储存与运移油气的作用，裂缝型储层成为非常规油气勘探的研究重点。裂缝型储层不同于均匀各向同性地层，由于定向排列近似垂直的裂缝，因此可等效为HTI介质，因而各向同性反射系数公式不适用于裂缝型储层。

基于反射系数近似公式，可建立地震数据与介质弹性参数之间的联系，Rüger反射系数近似公式的提出奠定了各向异性介质方位AVO正演和反演的理论基础。基于对裂缝物性参数与AVO方位特征的研究，刘洋等[15]认为裂缝倾角的变化影响方位AVO特征；毛宁波等[16]基于Rüger反射系数近似公式对四类含气裂缝型储层的AVO特征进行了研究；刘百红等[17]研究了裂缝密度、裂缝方位和裂缝填充物对地震波方位AVO的影响。近年来，为了提高各向异性储层油气勘探精度，宽方位高密度地震勘探的应用趋于普遍，获得的叠前地震道集同时具有炮检距和方位信息，基于“五维”(三维坐标+炮检距+方位角)叠前地震道集的地震资料处理技术也得到了发展。众多学者以Rüger近似公式作为各向异性理论基础展开了研究：刘依谋等[18]、印兴耀等[19]从地震采集、处理和解释各方面对宽方位地震勘探进行了系统的描述与讨论；基于Vermeer[20]与Cary[21]提出的OVT(Offset Vector Tile，炮检距向量片)概念，詹仕凡等[22]建立了方位角—炮检距叠加模板，采用多尺度、多方位各向异性分析对基于五维地震道集的地震属性分析技术进行了研究；党青宁等[23]、古发明等[24]、林娟等[25]将OVT域处理技术应用于实际地震数据。但是前人研究表明，Rüger近似公式仅在小炮检距范围内具有较高精度，基于Rüger近似公式的“五维”地震正演模拟与分析不能充分发挥“五维”地震数据丰富的炮检距信息。

本文根据散射矩阵与介质分解理论，以HTI介质精确的反射透射系数公式为基础，推导了HTI介质PP波反射系数一阶扰动近似公式，提高了中远炮检距反射系数的精度，从而提高“五维”叠前地震数据中远炮检距信息的利用率，为利用中远炮检距信息进行弹性参数反演提供了理论基础。

1 HTI介质反射系数一阶扰动近似定量表征

根据介质等效理论，地下发育有高角度近垂直裂缝的储层可等效为具有水平对称轴的横向各向同性介质(HTI介质)。基于弱各向异性假设，Rüger引入类似Thomsen各向异性参数，利用五个弹性参数对HTI介质刚度矩阵

(1)

进行表征，即

式中：δ(V)、ε(V)、γ(V)为Thomsen各向异性参数；ρ为介质密度；VP0为P波垂直入射到介质中的速度，VS0为SH波垂直入射到介质中的速度。

李春鹏[10]基于HTI介质刚度矩阵，在位移连续与应力连续的条件下得到的HTI介质反射透射系数精确公式为

(3)

可以表示为

MR=N

(4)

式中：M和N为系数矩阵，与入射波、散射波相关；R为仅考虑P波入射的散射矩阵。

考虑双层介质，假设介质为弱各向异性介质，且弹性界面两侧参数变化较小，基于散射理论与介质分解理论，可将M、R、N分解为背景项与扰动项的形式

(5)

式中：Mu、Ru、Nu为背景项，弹性参数不发生变化，不具有方位特征； ΔM、ΔR、ΔN为一阶扰动项，与弹性参数的一阶扰动变化和各向异性参数有关，具有方位特征。

由于介质各向异性程度较弱，可忽略各向异性参数高阶项，HTI介质qP波、qSV波和SH波相速度可近似为

(6)

式中：θP为纵波入射角、反射角或透射角；θSV为SV波反射角或透射角；θSH为SH波反射角或透射角；φ为观测方位角；φ0为测线与介质对称轴的夹角。由式(5)可看出，相速度与该层介质弹性参数有关。在弹性界面两侧参数变化较小的条件下，界面两侧弹性参数也可以扰动形式定义为

(7)

(8)

(9)

(10)

(11)

(12)

式中：VP01、VS01为垂直入射到上覆介质中的纵横波速度，ρ1为上覆介质的密度；VP02、VS02为垂直入射到下伏介质的纵横波速度，ρ2为下伏介质的密度；θP1、θSV1、θSH1为上覆介质纵波入射角或反射角、SV波反射角与SH波反射角；θP2、θSV2、θSH2为下伏介质纵波透射角、SV波透射角与SH波透射角；上划线表示界面两侧参数的均值；“Δ”表示界面两侧参数的差值。

将式(5)代入式(4)，有

(Mu+ΔM)(Ru+ΔR)=(Nu+ΔN)

(13)

假设背景介质弹性参数不变，即仅考虑均匀各向同性情况，则有

MuRu=Nu

(14)

在背景介质为均匀各向同性介质情况下，P波入射时介质中不存在反射P波，且不产生转换波，因此在式(15)中，Ru中仅有P波透射系数为1，矩阵中的其余系数为0，即

Ru=(000100)T

(15)

由于弹性界面两侧参数变化较小，且介质各向异性程度较弱，可忽略ΔM、ΔN二阶及高阶项，整理可得

R=Ru+ΔR=Ru+(Mu)-1(ΔN-ΔMRu)

(16)

将式(15)代入式(16)，整理可得

R=(ΔRPPΔRPSVΔRPSHΔTPP+1ΔTPSVΔTSH)T

(17)

上式即为P波入射时弹性界面上的纵横波反射透射系数近似公式。忽略弹性参数高阶项与各向异性参数高阶项，对式(17)进行化简整理可得(详细推导见附录A)

RPP(θ,φ)

(18)

上式即为基于方位观测系统的HTI介质P波入射情况下P波反射系数一阶扰动近似公式。若定义的测线方向与介质对称轴方向平行，则式(18)可简化为

RPP(θ,φ)

(19)

若弹性界面上覆介质为各向同性介质，忽略式(19)中的各向异性参数项，可得

(20)

上式即为Aki-Richards近似公式。由此可知，当地震波入射HTI介质时，所产生的响应特征可看作各向同性背景下地震波的响应特征与各向异性扰动的响应特征之和，且仅考虑一阶扰动近似时，HTI介质方位信息受控于各向异性参数，仅有各向异性参数扰动项具有方位特征。因此，基于散射矩阵的HTI介质一阶扰动近似公式推导具有合理性。

2 HTI介质PP波反射系数一阶扰动近似公式精度分析

为了验证上述推导公式精度，设计三层模型进行正演模拟：模型Ⅰ第一层为各向同性介质，第二层为HTI介质，第三层为各向同性介质；模型Ⅱ三层均为HTI介质(图1)。以第一层介质表面为xoy平面，z轴垂直xoy面向下表示地层深度，建立三维观测坐标系。

图1 三层模型方位观测系统示意图

2.1 模型Ⅰ正演分析

模型Ⅰ的三层介质弹性参数如表1所示。

表1 模型Ⅰ弹性参数

图2为模型Ⅰ利用本文所推导的公式与HTI介质反射系数精确公式、Rüger近似公式、各向同性Wang二阶近似公式[26]所计算的纵波反射系数曲线。三个近似公式的纵波反射系数曲线在小入射角时都有较高的精度，然而由于忽略了弹性参数高阶项信息，随着入射角的增大，近似公式与精确公式的误差逐渐增大。由图2a的各向同性/HTI界面的纵波反射系数特征曲线可知，本文所推导的一阶扰动近似公式与反射系数精确公式的误差较小，与Rüger近似公式相比具有更高的精度。图2b为HTI/各向同性界面的纵波反射系数曲线，随着炮检距的增大，Rüger近似公式与一阶扰动近似公式出现差异，在一定入射角范围内，Rüger近似公式精度较高，但一阶扰动近似公式与精确公式特征曲线变化趋势一致，说明了弹性参数高阶项对近似公式精度的影响。

当上覆介质为各向同性介质、下伏介质为HTI介质时，各向同性二阶近似公式精度远高于两类线性近似公式。由于不考虑各向异性参数项，图2a仅反映了纵横波速度、密度高阶项对近似公式精度的影响。当上覆介质为HTI介质，下伏介质为各向同性介质时，一阶扰动近似公式精度高于各向同性二阶近似公式(图2b)。

本文所推导一阶扰动近似公式与Rüger近似公式的误差主要是由于对各向异性参数项的表征不同。基于上述介质分解理论，纵波反射系数近似公式可分解为各向同性反射系数项与各向异性反射系数项，本文所推导的一阶扰动近似公式与Rüger近似公式具有相似的各向同性反射系数项，因此两个公式的误差主要受控于各向异性反射系数项的定量表征。同时也说明了研究高阶扰动近似公式对提高大入射角反射系数精度具有重要意义。

基于表1中模型参数，利用式(19)计算弹性界面处的方位纵波反射系数RPP，得到纵波反射系数RPP随入射角和方位角变化的曲面(图3)。

对于各向同性/HTI界面，在入射角较小时，反射系数方位特征不明显，随着入射角的增大，反射系数随方位角的变化特征逐渐明显，变化特征可表示为一条周期为π的余弦曲线(图3a)。HTI介质具有水平对称轴，平行于对称轴方向的各向异性特征最为明显，垂直于对称轴方向不具有各向异性特征，因此，基于测线方向与HTI介质对称轴方向相同的假设，受各向异性参数项的影响，平行于测线方向(方位角为0°)的纵波反射系数曲线随入射角变化的幅度最大，垂直于测线方向(方位角为90°)的纵波反射系数曲线随入射角变化的幅度最小。对于HTI/各向同性界面，纵波反射系数也具有相似的方位变化特征(图3b)。因此，可利用HTI介质的方位AVO特征进行弹性参数反演。

2.2 模型Ⅱ正演分析

模型Ⅱ中三层介质均为HTI介质，弹性参数如表2所示，假设HTI介质对称轴与测线方向平行。

图4为利用一阶扰动近似公式、Rüger近似公式与HTI介质反射系数精确公式计算的模型Ⅱ不同方位角的纵波反射系数曲线。与模型Ⅰ结果相似，小入射角时，利用三个公式所计算的纵波反射系数特征曲线拟合度较高，具有较高的精度；由于忽略了弹性参数高阶近似项，在中、大入射角时，近似公式与精确公式的误差逐渐增大。上界面的纵波反射系数特征曲线(图4a)，一阶扰动近似公式比Rüger近似公式具有更高的精度。下界面的纵波反射系数特征曲线(图4b)，与模型Ⅰ结果相似，在中入射角时，Rüger近似公式与一阶扰动近似公式出现误差，但基于一阶扰动近似公式所算得的反射系数曲线与精确公式的曲线具有相似的变化趋势。可见，本文所推导的一阶扰动近似公式与Rüger近似公式的误差随着方位角的变化而变化，随着方位角的增大，各向异性参数项对于纵波反射系数的影响逐渐减小，当方位角为90°时，各向异性参数为0，此时弹性分界面两侧均为各向同性介质，反射系数近似公式仅受控于纵横波速度项与密度项。

图2 模型Ⅰ纵波反射系数RPP曲线对比(方位角为0°)

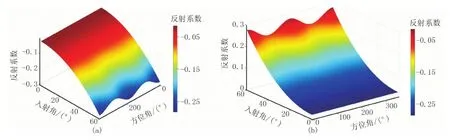
图3 模型Ⅰ纵波反射系数RPP曲面

层位纵波速度m/s横波速度m/s密度kg/m3γ(V)ε(V)δ(V)1290013302290-0.1-0.01-0.092280016202280-0.1-0.20-0.193290013302290-0.1-0.01-0.09

图5为模型Ⅱ纵波反射系数曲面，相比于模型Ⅰ纵波反射系数曲面，当纵波传播至HTI1/HTI2界面时，在小角度范围内，反射系数随方位角变化特征与模型Ⅰ相同，随着入射角的增大，反射系数随方位角变化的特征趋于明显。

由于模型Ⅱ界面两侧介质均为HTI介质，各向异性对界面处纵波反射系数的传播特征影响更为剧烈，因此相较于模型Ⅰ，在中远炮检距范围内，模型Ⅱ纵波反射系数随方位角的变化特征更为明显，当界面两侧介质为HTI2/HTI1时，纵波反射系数方位变化特征相似。

图4 模型Ⅱ方位角为0°(左)、45°(中)、90°(右)纵波反射系数RPP曲线对比

图5 模型Ⅱ纵波反射系数RPP曲面

综合分析图3与图5，本文所推导的扰动近似方程不仅适用于描述各向同性/HTI界面处的纵波反射系数特征，当界面两侧均为HTI介质时，该方程同样能够对界面纵波反射系数变化特征进行表述，证明了该方程具有较高的精度和一定适用性。

综上所述，纵波反射系数变化特征随炮检距的增大而增大，当测线方向与介质对称轴方向呈一定差值时，纵波反射系数特征也随之变化。基于在中远炮检距范围内纵波反射系数的变化特征，可进行介质弹性参数反演； 基于纵波反射系数在中远炮检距的方位变化特征，可进行裂缝预测。本文所推导的方位观测系统下纵波反射系数一阶扰动近似方程提高了中远炮检距纵波反射系数的精度，进而可更为明显地对HTI介质的方位AVO特征进行表征，达到提高参数反演与裂缝预测精度的目的。

3 结论与认识

本文以HTI介质精确反射透射系数公式为基础，根据散射矩阵与介质分解理论推导了HTI介质一阶扰动近似公式，在方位观测系统下计算两个三层模型的反射系数。

对于三层模型的上界面，本文所推导的HTI介质一阶反射系数近似公式比Rüger近似公式明显具有更高的精度，使中远炮检距信息的利用率得以提升。对于三层模型的下界面，本文所推导的近似公式精度低于Rüger近似公式，但曲线变化趋势与精确公式更加吻合。该公式可作为五维地震反演方法的理论基础，应用五维叠前地震数据中丰富的炮检距与方位角信息，能提高反演精度。

由于忽略弹性参数高阶项，该公式仅针对各向异性参数项反演精度有一定提升，若想进一步提高弹性参数反演精度，则需利用弹性参数高阶项，构建高阶近似公式。

附录A HTI介质方位观测PP波反射系数一阶扰动近似推导

基于弱各向异性假设，若测线方向与介质对称轴方向平行，忽略弹性参数高阶项，对相速度与波的偏振方向进行近似表征

(A-1)

(A-2)

(A-3)

(A-4)

式中

(A-5)

将上述近似表征代入系数矩阵，基于扰动思想与介质分解理论，可将矩阵分解为背景矩阵(Mu，Nu，Ru)与一阶扰动矩阵(ΔM，ΔN，ΔR)，其中背景矩阵元素为

(A-6)

(A-7)

(A-8)

式中

(A-9)

当仅背景介质为均匀各向同性介质时，反射系数背景矩阵可表示为

=[000100]T

(A-10)

对矩阵各参数取一阶扰动项，将背景项与一阶扰动项代入表达式

R=Ru+ΔR=(Mu)-1(ΔN-ΔMRu)

(A-11)

通过计算整理，可得到HTI介质方位观测五维一阶扰动近似公式

RPP(θ,φ)

(A-12)