一种改进的基于SM2的代理签名方案

宋靖文，张大伟，孟吴同，高 凡，刘晓东

(1.北京交通大学 计算机与信息技术学院 北京 100044；2.山东大学 网络信息安全研究所 山东 济南 250000)

0 引言

1996年，Mambo等[1-2]针对现实生活中数字签名权力的委托问题提出了代理签名的概念.代理签名可以看作是数字签名的扩展形式.RSA算法[3]、Elgamal算法[4]、Schnorr算法[5]是常用的可用于数字签名的算法，这些算法主要依赖于离散对数问题或大数因子分解问题.1985年，Koblitz和Miller[6-7]分别提出将椭圆曲线应用到公钥密码系统.椭圆曲线公钥密码体制依赖的椭圆曲线离散对数问题相较于前两类难题，更加难以求解.2003年白国强等[8]设计出基于椭圆曲线的代理数字签名；2005年张宁等[9]指出文献[8]中原始签名者也能生成有效的代理签名，对此进行了改进；2007年高胜[10]对文献[9]进一步改进，提高了方案效率.此外，其他基于椭圆曲线的代理签名的研究也在进行.2004年纪家慧等[11]改进了ECDSA，并提出新的代理签名体制；2007年左为平等[12]指出文献[11]存在原始签名者能伪造代理签名者的普通签名的情况，并提出避免此攻击的方案；2010年胡兰兰等[13]指出文献[12]中原始签名者仍可伪造代理签名，并进行改进；2017年郭青霄等[14]基于SM2算法[15]提出一种新的代理签名方案.一般来说，不采用授权书的代理签名方案存在一些固有的局限性[16].文献[14]中的方案也是如此，其安全性要由证书来保证，如果没有公开证书将代理签名者的身份和授权信息绑定，则方案不满足可识别性和不可否认性.

本文借鉴文献[17]中的授权信息的构造方法，在文献[14]方案的基础上加以改进，改进的方案将原方案中证书的信息加入到授权信息生成过程中，使得验证代理签名的同时也是在验证证书中的内容，从而无须额外生成和验证证书，提高效率的同时保证了代理签名的安全性.

1 代理签名

代理签名是指在代理签名方案中，被指定的代理签名者可以代表原始签名者生成有效的签名.

文献[1-2]指出代理签名应满足可验证性、可区分性、不可伪造性、可识别性和不可否认性等性质.之后，文献[18-19]在一定程度上加强了不可伪造性、可识别性、不可否认性的定义.

可以认为代理签名分为4大类：完全代理签名、部分代理签名、具有证书的代理签名[1-2]以及具有证书的部分代理签名[17].本文仅对后3类进行介绍.

部分代理签名中的代理签名密钥是由原始签名者的私钥计算生成的.代理签名者使用代理签名密钥进行签名，验证者仍使用原始签名者公钥进行验证，以确保签名消息得到了原始签名者的认可.

具有证书的代理签名方案需要借助证书来实现签名权力的委托.原始签名者需要使用私钥对同意授权某人的文件进行签名，生成授权证书.之后，代理签名者使用自己的私钥或原始签名者为其生成的代理签名密钥进行签名.验证者不仅要对代理签名进行验证，还要对证书进行验证.

具有证书的部分代理签名是部分代理签名和具有证书的代理签名的结合.原始签名者首先对授权文件签名，但不同于具有证书的方案，代理签名者会结合授权文件的签名和私有信息计算代理签名密钥，利用此密钥对消息签名.这样，代理密钥还是由原始签名者私钥计算出来的，验证者仍使用原始签名者公钥验证代理签名，但无需再验证授权文件的签名，既保证了安全性，又提高了效率.

文献[14]的方案虽然是部分代理签名，但可识别性和不可否认性仍需证书的保证，而证书的生成和验证会影响方案的效率，因此，本文将设计一种更加高效的具有证书的部分代理签名方案.

2 文献[14]的方案

2.1 初始化参数

选取SM2公钥密码算法[15]中推荐的椭圆曲线参数，G是椭圆曲线中阶为n的基点.假设Alice是原始签名者，私钥为dA∈[1,n-2]，公钥为PA=dAG，私钥保密，公钥公开；假设Bob是代理签名者，代表原始签名者Alice 签名；验证者Carol 对生成的代理签名进行验证.

2.2 代理授权

首先，Bob进行如下操作.

B1：用随机数生成器生成随机数kb∈[1,n-1]，计算椭圆曲线上的点Gb=kbG；

B2：Bob将Gb发送给Alice.

Alice收到来自Bob的信息后，进行下面的步骤：

A1：用随机数生成器生成随机数ka∈[1,n-1]，计算椭圆曲线上的点Ga=kaG；

A2：计算椭圆曲线上的另一个点Gab=(x1,y1)=kaGb；

A3：计算rab=x1modn，若rab=0则返回步骤A1；

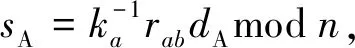
A5：Alice将(Ga,Gab,sA)作为授权信息发送给Bob.

其中：Ga和Gab需要公开并在证书中与Bob的身份绑定，而sA需秘密发送给Bob.

2.3 授权验证及代理密钥的生成

Bob收到授权信息后，对授权信息进行验证，验证过程如下.

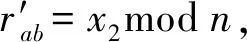
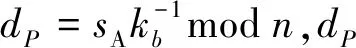
2.4 代理签名的生成

当Bob代替Alice对消息M进行签名时，Bob使用的签名密钥是dP，签名过程如下.

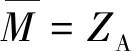
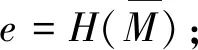
B8：用随机数生成器生成随机数k∈[1,n-1]，计算(x3,y3)=kGab；

B9：令r=(e+x3)modn，若r=0或r+k=n则返回步骤B8；

B10：计算代理签名s=((1+dP)-1(k-rdP))modn，若s=0则返回步骤B8；

B11：此时消息M的代理签名是(Ga,Gab,r,s).

2.5 代理签名的验证

为了验证收到的消息M′及其代理签名(Ga,Gab,r′,s′)，验证者Carol进行以下验证步骤.

C1：检验r′∈[1,n-1]和s′∈[1,n-1]是否成立，若不成立则验证不通过；

C3：计算rab=x1modn；

C4：计算t=(r′+s′)modn，若t=0，则验证不通过；

2.6 方案存在的不足

文献[14]方案的某些性质依赖授权证书的存在.若没有证书，则验证者不能识别出代理签名生成者的身份；若一个原始签名者授权了多个代理签名者，则代理签名者可以对自己生成的有效代理签名进行否认，方案不满足不可否认性.此外，代理签名者可以利用已知信息伪造其他授权信息和代理签名密钥，进而伪造代理签名.虽然伪造的代理签名仍是由代理签名者生成的，看似对方案的安全性威胁不大，但若代理签名者为逃避责任每次都用伪造的代理签名密钥进行签名，而验证者在不知情的情况下接受了伪造的代理签名，那么当需要确定代理签名者身份时，即使原始签名者记录了授权信息与代理签名者身份的对应关系，也无法找出代理签名的真正生成者.

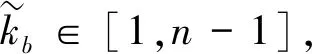
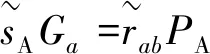
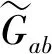
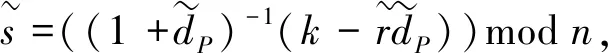
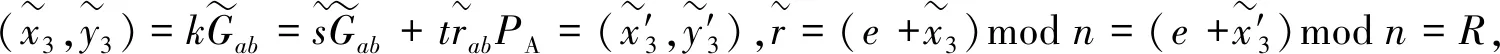
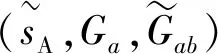
3 改进的方案

3.1 初始化参数

mW：授权证书信息，可以包含原始签名者及代理签名者的身份信息、代理签名者的权限等.

其他参数与文献[14]相同.

3.2 代理授权

此阶段的步骤B1～B2及步骤A1～A3与2.2节相同，其他步骤为

A4： 计算e0=H(mW‖rab)；

A6： Alice将(mW,Ga,Gab,sA)作为代理签名的授权信息发送给Bob.

其中：mW、Ga和Gab需要对外公开，而sA需秘密发送给Bob.

3.3 授权验证及代理密钥的生成

Bob验证授权信息.

B4： 计算e0=H(mW‖rab)；

3.4 代理签名的生成

Bob使用密钥dP对消息M进行签名，签名过程同文献[14]，代理签名的形式变为(mW,Ga,Gab,r,s).

3.5 代理签名的验证

为了验证收到的消息M′及其数字签名(mW,Ga,Gab,r′,s′)，验证者Carol应执行以下操作.

C1： 检验r′∈[1,n-1]和s′∈[1,n-1]是否成立，若不成立则验证不通过；

C3： 计算rab=x1modn；

C5： 计算t=(r′+s′)modn，若t=0，则验证不通过；

3.6 正确性验证

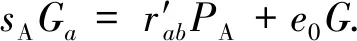
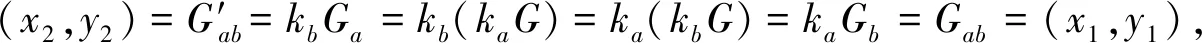
3.6.2代理签名验证的正确性 当Carol收到正确的签名(mW,Ga,Gab,r′,s′)时，应有R=r′.

即k=(s′+dPt)modn，得

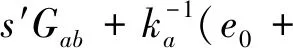
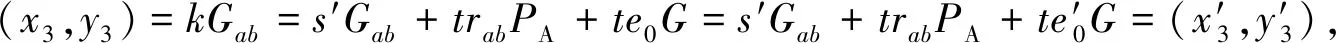
3.7 安全性分析

改进方案的安全性仍然是基于哈希函数的单向性和椭圆曲线离散对数问题的困难性.

3.7.1不可伪造性 1) 原始签名者的普通签名的不可伪造性

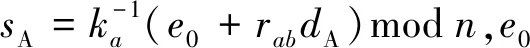
2) 授权信息的不可伪造性

i) 未被授权的攻击者伪造授权信息.伪造有效的授权信息等价于求(mW,Ga,Gab,sA)，使得sAGa=rabPA+e0G成立，e0=H(mW‖rab).e0是哈希函数值，哈希函数具有单向性，因此，攻击者必须先确定mW和rab的值.rab=x1modn，x1是Gab的横坐标，故也要确定Gab的值，由此，rabPA+e0G的值确定.

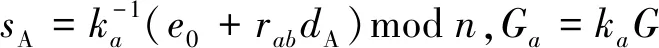
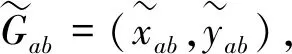
3) 代理签名的不可伪造性

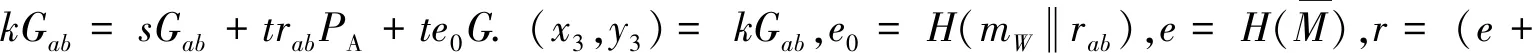
如果通过构造k来确定(r,s)的值，因为(x3,y3)=kGab，r=(e+x3)modn，根据k、e和Gab的值可以进一步计算出r.由kGab=sGab+trabPA+te0G和t=(r+s)modn，可以得到kGab-r(rabPA+e0G)=s(Gab+rabPA+e0G)，此时求解s意味着求解椭圆曲线离散对数问题.

如果通过构造(r,s)来确定k的值，无论是根据kGab=sGab+trabPA+te0G对k进行求解，还是根据r=(e+x3)modn和(x3,y3)=kGab进行求解，都是求解椭圆曲线离散对数问题.

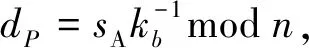
3.7.2可区分性 1) 代理签名(mW,Ga,Gab,r,s)的形式与普通签名(r,s)的形式不同.2) 即使对同一代理签名者进行多次授权，也可以对不同授权情况下生成的代理签名加以区分.这是因为，原始签名者和代理签名者在每次授权过程中，生成的授权信息不同.3)mW中有代理签名者的身份信息，所以不同代理签名者生成的代理签名之间也可以区分.

3.7.3可识别性和不可否认性 有效代理签名(mW,Ga,Gab,r,s)中的mW不能被包括代理签名者在内的任何人篡改.因此，一旦有效的代理签名被生成，就可以通过mW识别出代理签名者的身份，使得代理签名者无法进行否认.

4 方案实现

实验主机配置为1.80 GHz、i5-3337U CPU、4 GB RAM，系统为Ubuntu16.10，编程语言为Golang1.7.6.

4.1 初始化参数

4.1.1椭圆曲线参数 采用SM2椭圆曲线公钥密码算法标准[15]推荐的素数域256位椭圆曲线，即y2=x3+ax+b.对于曲线参数，同样采用SM2椭圆曲线公钥密码算法标准[15]中的推荐，如表1所示.

表1 SM2公钥密码算法椭圆曲线参数[15]Tab.1 Elliptic curve parameters of SM2 public key cryptography algorithms[15]

4.1.2原始签名者公私钥 原始签名者的公私钥如图1所示.

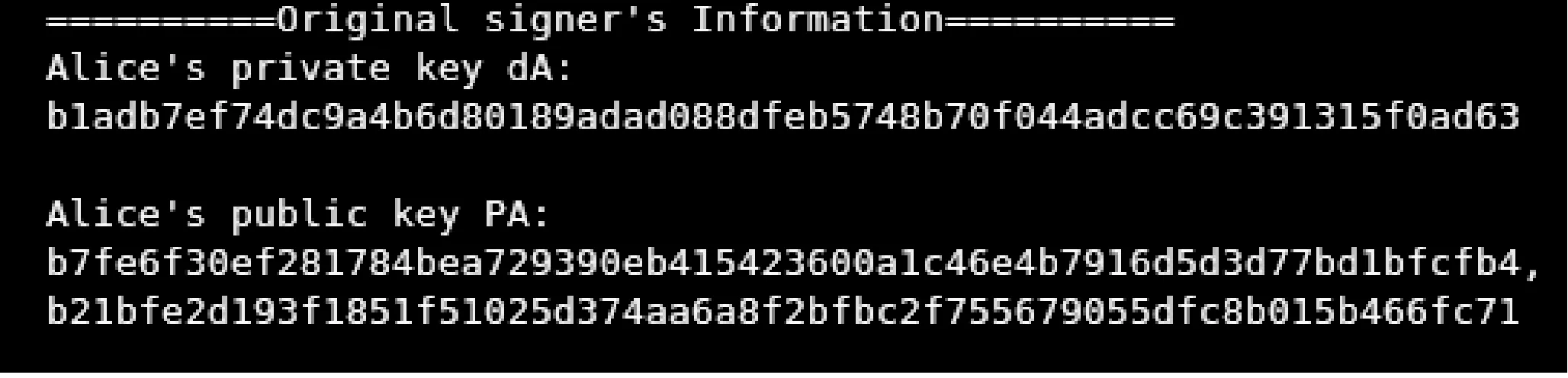
图1 原始签名者的公私钥信息Fig.1 The public key and private key of the original signer

4.2 方案各阶段实验结果

代理授权的生成、代理授权的验证及代理密钥的生成、代理签名的生成和代理签名的验证的实验结果分别如图2～5所示.

4.3 方案复杂性

文献[14]中的方案除授权信息的生成外还有授权证书的生成.此外，验证者验证代理签名时需要进行两次验证：一次是证书上签名的验证，另一次是代理签名的验证.假设文献[14]中证书上的签名为标准SM2数字签名，表2是对标准SM2数字签名、文献[14]中的代理签名方案与改进的SM2代理签名方案的复杂性比较，由于Hash运算速度很快，椭圆曲线上的加法运算也很高效[20].故本文主要对点乘次数TM、表示模乘次数TMM、表示模逆次数TINV进行比较.实验对3种方案的签名和验证时间进行了多次测试，计算得到的平均时间如表3所示.

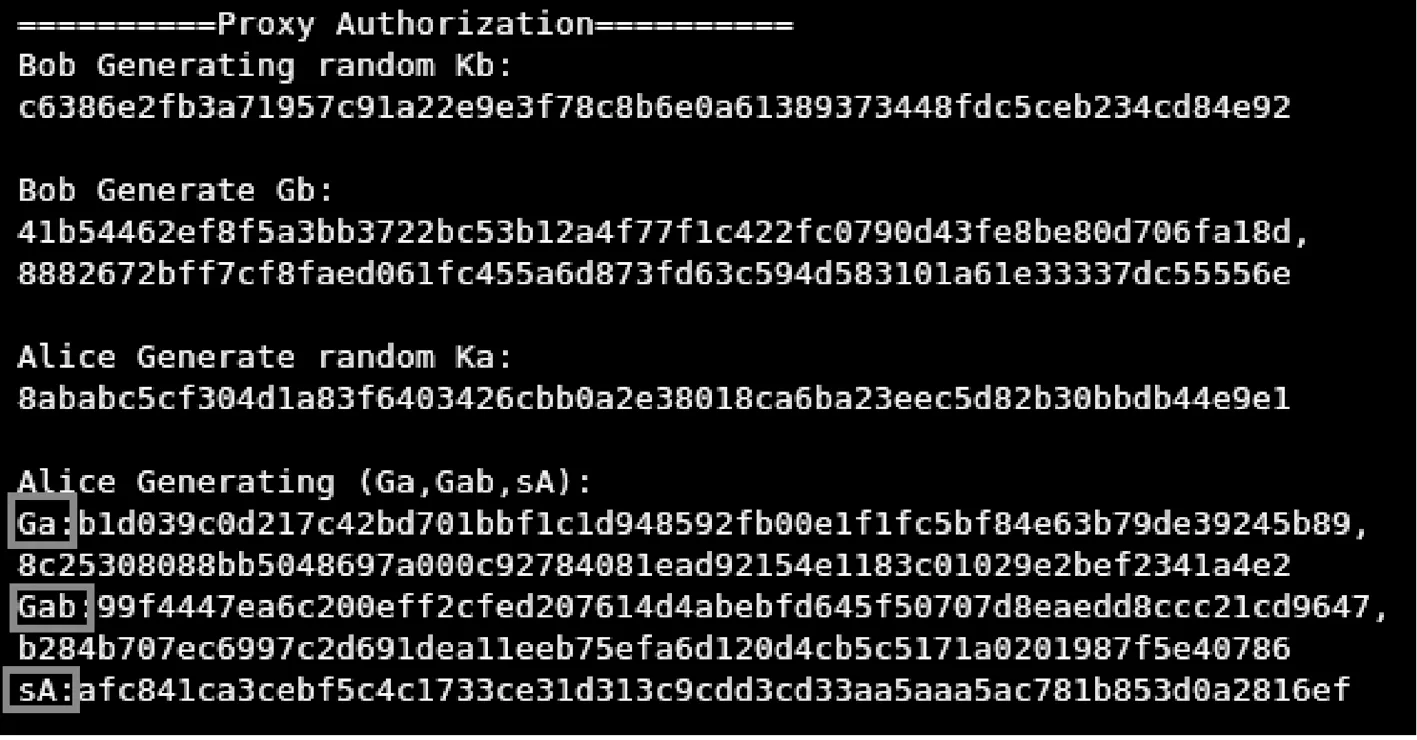
图2 代理授权生成阶段结果Fig.2 The results of proxy generation

图3 代理授权验证及代理密钥生成阶段结果Fig.3 The results of proxy verification and proxy key generation

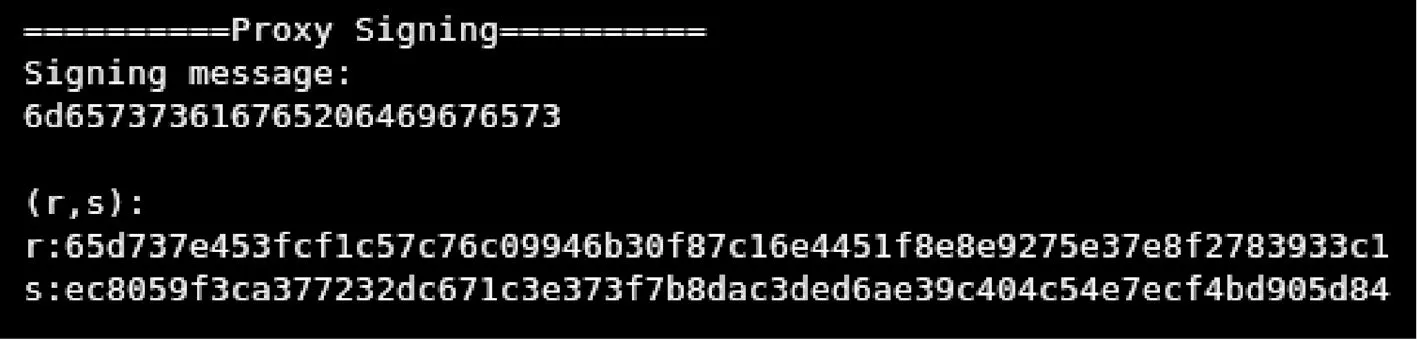
图4 代理签名生成阶段结果Fig.4 The results of proxy signature generation

图5 代理签名验证阶段结果Fig.5 The results of proxy signature verification

表2 三种方案的复杂性比较Tab.2 Comparison of the complexity of three schemes

表3 三种方案的签名和验证速度比较Tab.3 Comparison of signing and verification speeds of three schemes ms

由表3可见，标准SM2数字签名、原SM2代理签名方案和改进的代理签名方案的签名生成时间相差不大，这是因为两种代理签名方案中的签名算法与标准SM2签名算法所需运算次数相同；原SM2代理签名方案中，总验证时间约是标准验证时间的2.03倍，原因是总验证时间等于证书验证时间与代理签名的验证时间之和；改进后的代理签名方案的验证时间接近标准SM2验证时间的1.5倍，这是由于代理签名验证过程比标准签名验证过程多了两次数乘运算和一次点乘运算.从总体上来说，改进方案的代理签名生成效率与文献[14]中的方案相近，验证效率提高了约26%.

5 总结

本文分析并指出了文献[14]方案的不足，并进行了改进.改进的方案无需可信任方生成证书，但仍能满足可验证性、不可伪造性、可区分性、可识别性和不可否认性.与原方案相比，虽然改进的方案中增加了部分运算，但减少了原方案中证书的生成和验证过程.总体来说，改进方案的效率比原方案有所提高.