基于小波包和概率神经网络算法的短路故障识别方法

栾 翔，张 琪，王维信

（国网山东青岛市黄岛区供电公司，山东 青岛 266400）

0 引言

随着世界一流配电网建设的不断推进，电网规模不断扩大，输电线路故障对整个电网的影响不容忽视。系统一旦发生故障，必须第一时间采取措施，否则故障分量将对线路以及高压设备造成严重后果。因此，既准确又快速地判断故障类型并采取相应措施是非常必要的。

人工智能［1］技术在故障诊断与分析方面已经有了更深层次的发展。已有较多文献对故障识别进行了研究，产生了多种故障识别方法，文献［2］利用神经网络来模拟元胞的全套保护，但需要与其他元胞的诊断结果相结合，增加了诊断难度，其结果具有一定的随机性。文献［3］采用贝叶斯故障诊断方法，通过信息采集系统对故障区域范围进行锁定，利用贝叶斯网络进行反向推理从而获得故障元件。此方法结构较为复杂，计算步骤较多，诊断时间较长，不适合在线监测预警。文献［4］采用一对一多类支持向量机的方法实现故障分类，该方法能够有效融合支持向量机的泛化性和粗糙集的不完备信息，从而达到较高的诊断正确率。概率神经网络是完全前向的计算过程，结构简单，训练简洁，有效避免陷入局部极小，有较强的容错能力，同时可以满足小样本的识别精度。

研究基于小波包和概率神经网络算法的短路故障识别方法，利用小波包对故障参数进行分解，提取各频段的能量值，对能量值进行归一化处理，构造概率神经网络训练样本的特征向量，将训练样本作为概率神经网络的输入，测试样本对训练结果进行测试。

1 小波包和概率神经网络算法简介

1.1 小波包简介

小波包分解具有信号时频分析的性质，可以将信号投影到中心频率不同但带宽相同的小波包基函数的空间中，具有良好的时频分辨率。在实际应用中，小波包分析［5-6］能够对低频信号和高频信号提供更加精细的分析方法，通过提取样本信号的特征值，得到与之相匹配的最佳的基函数，从而对故障信号提供更准确的分析方法。

小波包［7］分析通过信号的分解与重构对采样信号进行分析：首先对低频信号和高频信号进行分解，得到不同空间尺度上的基波系数以及各次谐波分量系数；然后根据低频与高频信号系数，重构出基波信号和各次谐波信号，从而提高信号的时频分辨率。

图1为小波包3层分解示意，其中A表示低频段，D表示高频段。

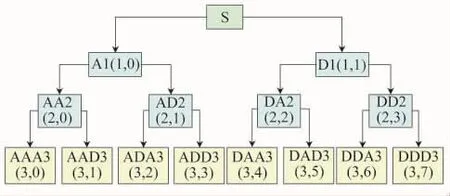
图1 小波包分解树结构

利用图1所示小波包分解树对采样信号进行n 层分解重构，用 Snj（j=0，1，…，2n-1）代表第 n 尺度2n个结点的频率范围。归一化后，最低频率S30为0，最高频率S37为1，3层分解小波包对应的频率成分代表的频率范围如表1所示。

表1 各频率成分所代表的归一化频率范围

在不同的频率段内提取到目标频率后，需要对该频段内的能量进行计算。各个频带Snj对应的能量为 Enj（j=0，1，…，2n-1），有：

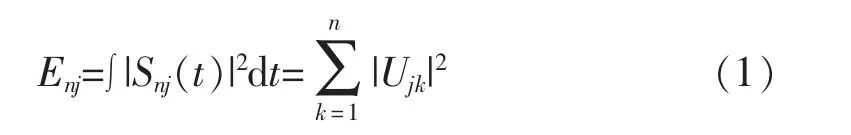
式中：Ujk（j=0，1，…，7；k＝1，2n-1，…，n）为重构信号Snj的离散点的幅值。

构造被测零序电流的特征向量，以3层分解为例，特征向量为

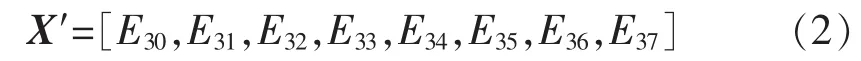
为满足数据处理的方便性以及归纳统一样本的统计分布性的要求，将特征向量X′进行归一化处理，其计算公式为

得到归一化特征向量为

1.2 概率神经网络算法简介

概率神经网络［8-9］（probabilistic neural network，PNN）实质是贝叶斯最小风险准则发展而来的一种并行算法，是一种常用语模式分类的神经网络。PNN作为径向基网络［10］的一种，具有训练时间短，分类正确率高等优点。

PNN的层次模型由输入层、模式层、求和层、输出层组成，基本结构如图2所示。

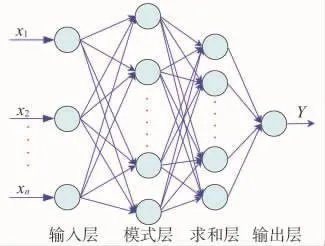
图2 概率神经网络基本结构

输入层负责将特征向量传入网络，输入层个数即样本特征向量X的个数；模式层通过连接权值与接入层连接，将输入节点传递来的输入向量进行加权运算，如式（5）所示；求和层将各个模式层单元连接起来，并将输入进行求和；输出层负责求和层中输出最大者对应的状态模式，如式（6）所示。

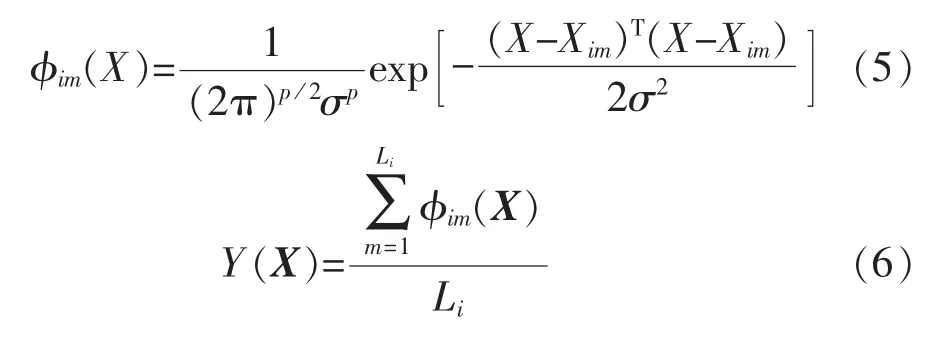
式中：i为故障模式，i=1，2，3，分别表示单相故障、两相故障和三相故障；p为训练样本的维度；σ为平滑因子；Xim为故障模式i的第m个样本数据中心；Li为故障模式i的训练样本总数。

2 算例仿真研究

2.1 利用小波包提取能量特征向量

利用Matlab／Simulink建立35 kV中性点经消弧线圈接地仿真模型，如图3所示。在仿真模型中，电源输出三相电压为35kV，内部接线为Y形连接。输电线路Line1～Line4长度分别为 130km，175km，1km，150 km，线路负荷Load1，Load2，Load3有功负荷分别为1.0MW，0.2 MW，2.0 MW，其他参数均采用默认参数。

图3 35kV系统故障仿真模型

设置Fault1，在0.2 s时刻发生短路接地故障，运行仿真模型，观察短路后零序电流信号重构系数如图4～6所示。

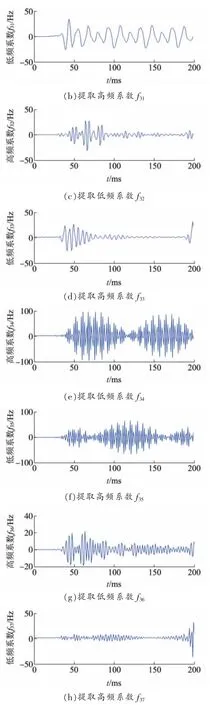
图4 单相短路小波包分解重构系数

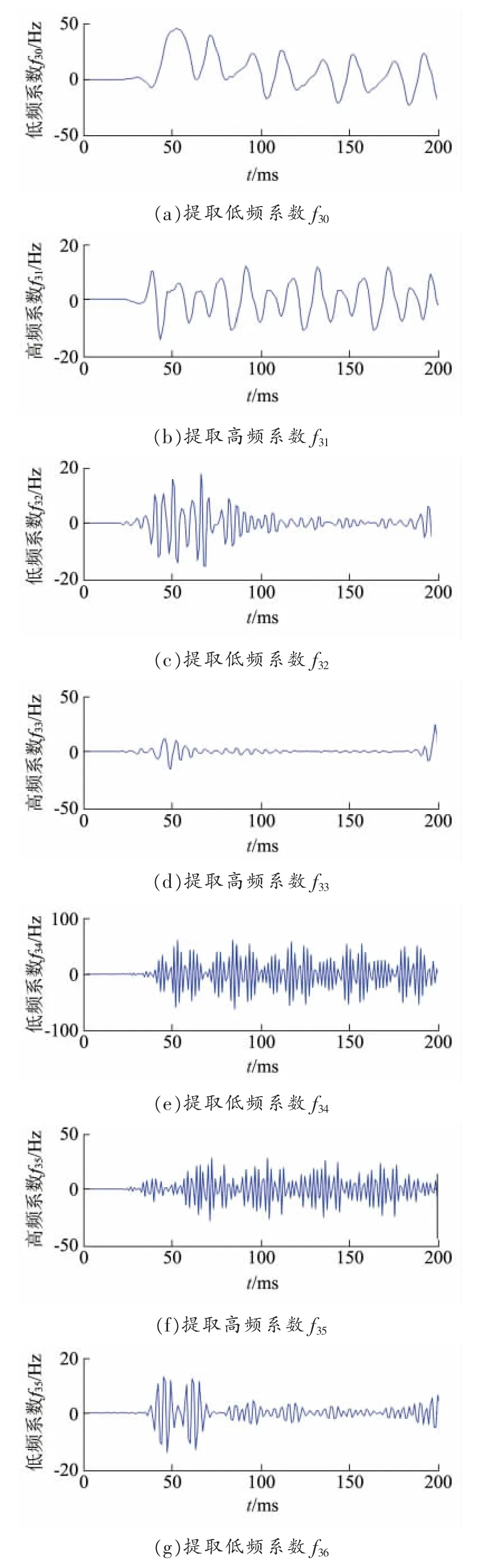
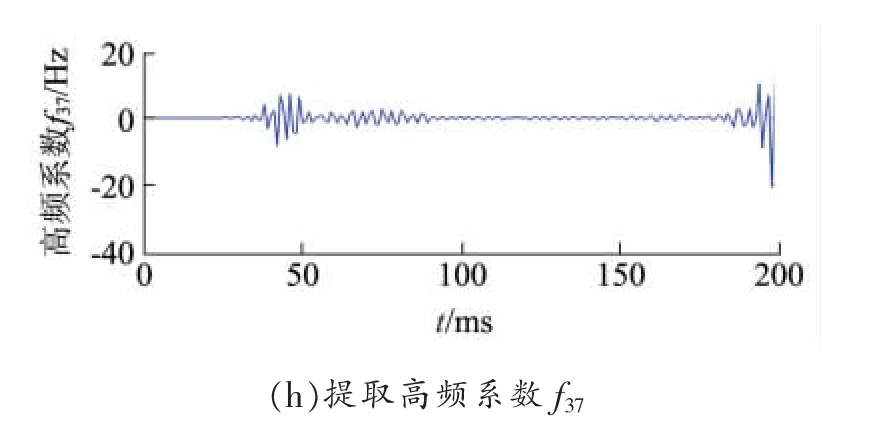
图5 两相短路小波包分解重构系数

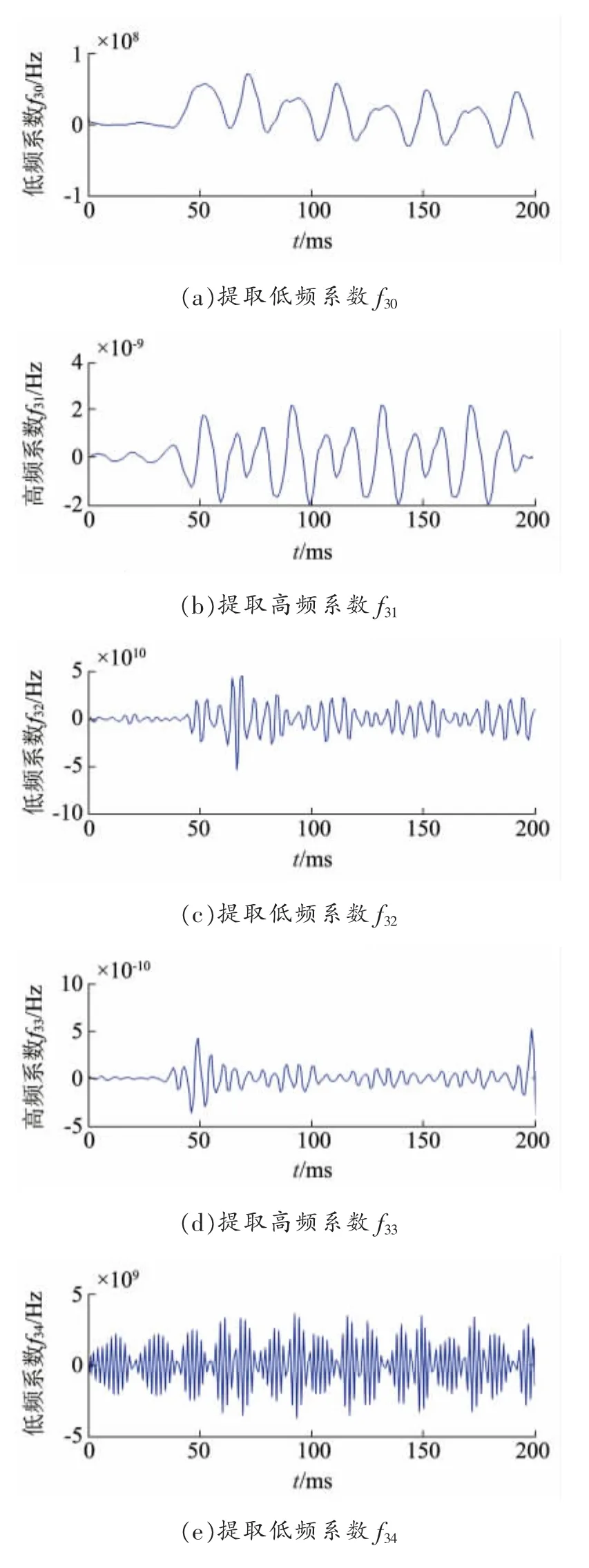
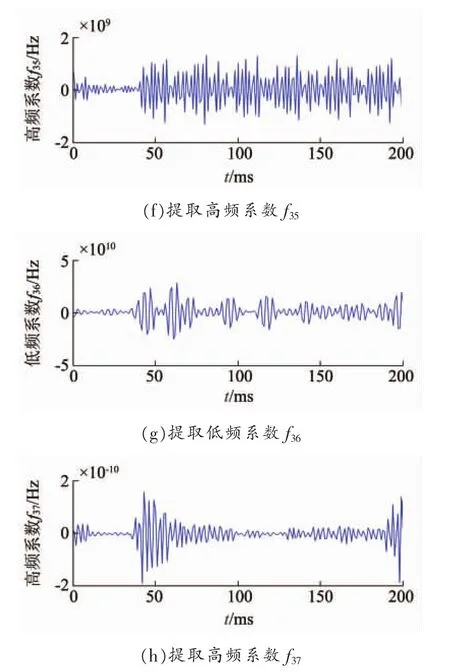
图6 三相短路小波包分解重构系数

利用式（2）～（4）进行计算，构造 8 个能量特征向量，作为PNN网络的输入。选取一组计算后的能量值如表2所示。

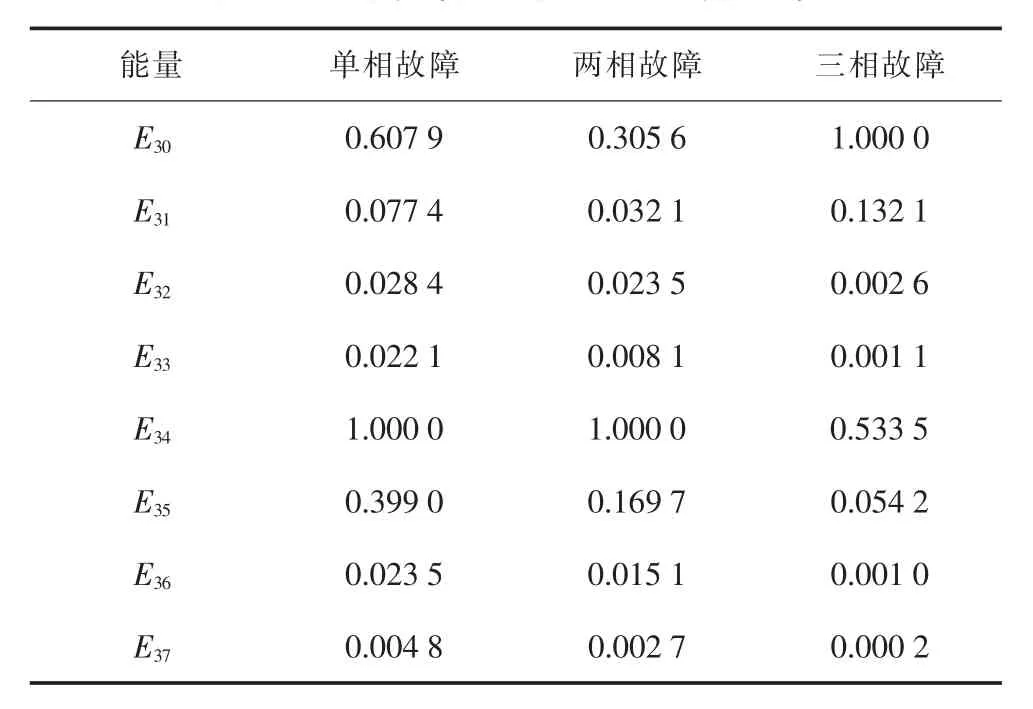
表2 不同故障归一化处理后的能量值

2.2 PNN网络的训练与测试

PNN通过调用Matlab函数newpnn来建立扰动信号分类程序。通过PNN的调用格式：

调用命令中P为输入样本向量，T为目标分类向量。SPREAD为分布密度，扰动分类的准确率与训练样本数和newpnn函数参数SPREAD值有关，SPREAD值过大，密度估计比较平滑但细节丢失严重，SPREAD值过小，密度估计会呈现较多的尖峰突起。

设置不同的故障类型，每种故障分别采集20组样本作为训练概率神经网络的输入样本进行训练，共得到60组训练结果。针对此训练结果，在仿真实验中选取30组测试样本进行测试，将特征向量的输入定义为60组训练样本和30组测试样本。

根据上述方法利用MATLAB对训练样本进行PNN训练及测试，利用试凑法得到SPREAD最佳值为0.9。PNN训练后的效果及误差如图7～8所示，PNN网络的测试样本分类效果如图9所示。

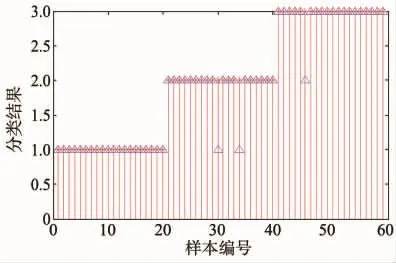
图7 PNN网络训练

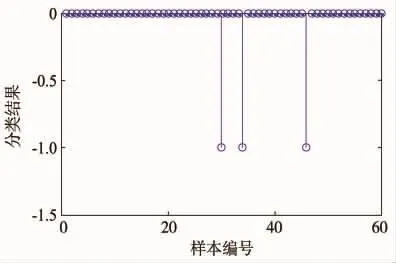
图8 PNN训练后的误差

由图7和图8可见，将训练样本作为输入对训练结果进行反测试时，共有3个样本出现误差，即准确率为95%。

由图9可知，当利用训练结果对测试样本进行验证时，只有一个样本出现了错误，即总的判断准确率为96.7%。经过训练后的PNN准确率表明，最后得到的训练结果可以对故障类型进行识别。

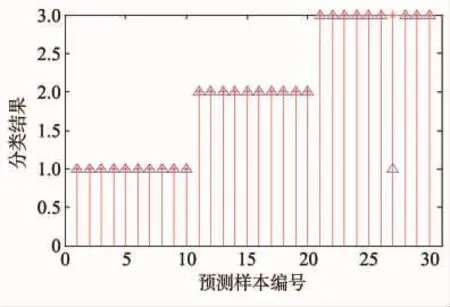
图9 预测网络数据的分类效果

3 结语

利用小波包对故障分量进行分解与能量值提取，构造概率神经网络训练样本特征向量，将培训结果利用测试样本进行验证，可以达到较高的故障识别准确度。通过Matlab／Simulink仿真实验表明，PNN的非线性分类能力强，在最小风险准则下对短路故障进行识别，训练速度快、识别精度高、有较强的容错能力，具有理想的识别效果。