塔腿加过渡段输电塔地震响应时程分析

吴景天 ，邓洪洲 ，李 焱，郭艳军 ，董 斌

（1.同济大学建筑工程系，上海 200092；2.国网四川省电力公司，四川 成都 610041；3.四川电力设计咨询有限责任公司，四川 成都 610041）

0 引言

成兰铁路阿坝松潘牵引站供电工程位于四川省阿坝州茂县—松潘地区，线路所在区域山高坡陡，当坡度超过一定限度时，常规高低腿铁塔无法满足高差要求。对铁塔进行改造时，不能直接将铁塔长腿加高以增大高低腿高差，塔身坡度不变时，塔腿主材与斜材的夹角随塔腿高度的增加而减小，目前塔腿设计时主斜材夹角一般控制在18°以上。而如果采用对陡峻山区基础进行改造的大开挖方式，不仅增加施工成本和建设周期，同时还破坏植被、环境。

输电塔塔腿加过渡段设计目的是解决陡峻山区立塔困难的问题，以期降低基础造价和塔材重量，减小基坑开挖量，将输电线路工程建设对环境的影响降低到最低，同时方便施工，降低成本。

对于普通平腿输电塔的地震响应，已经有学者做过一些研究［1-4］。 高荣誉等［5］采用 SAP2000 对常规长短腿直线输电塔在地震作用下的动力时程响应进行了分析。贾玉琢等［6］基于时程分析法分析了常规长短腿猫头直线塔地震响应。但目前对塔腿加过渡段输电塔的地震动力时程响应则尚无研究。

以工程中500 kV的SZC4直线塔为研究对象，采用ANSYS有限元分析软件进行输电塔地震动力时程响应分析，为塔腿加过渡段输电塔的设计提供依据。

1 分析模型

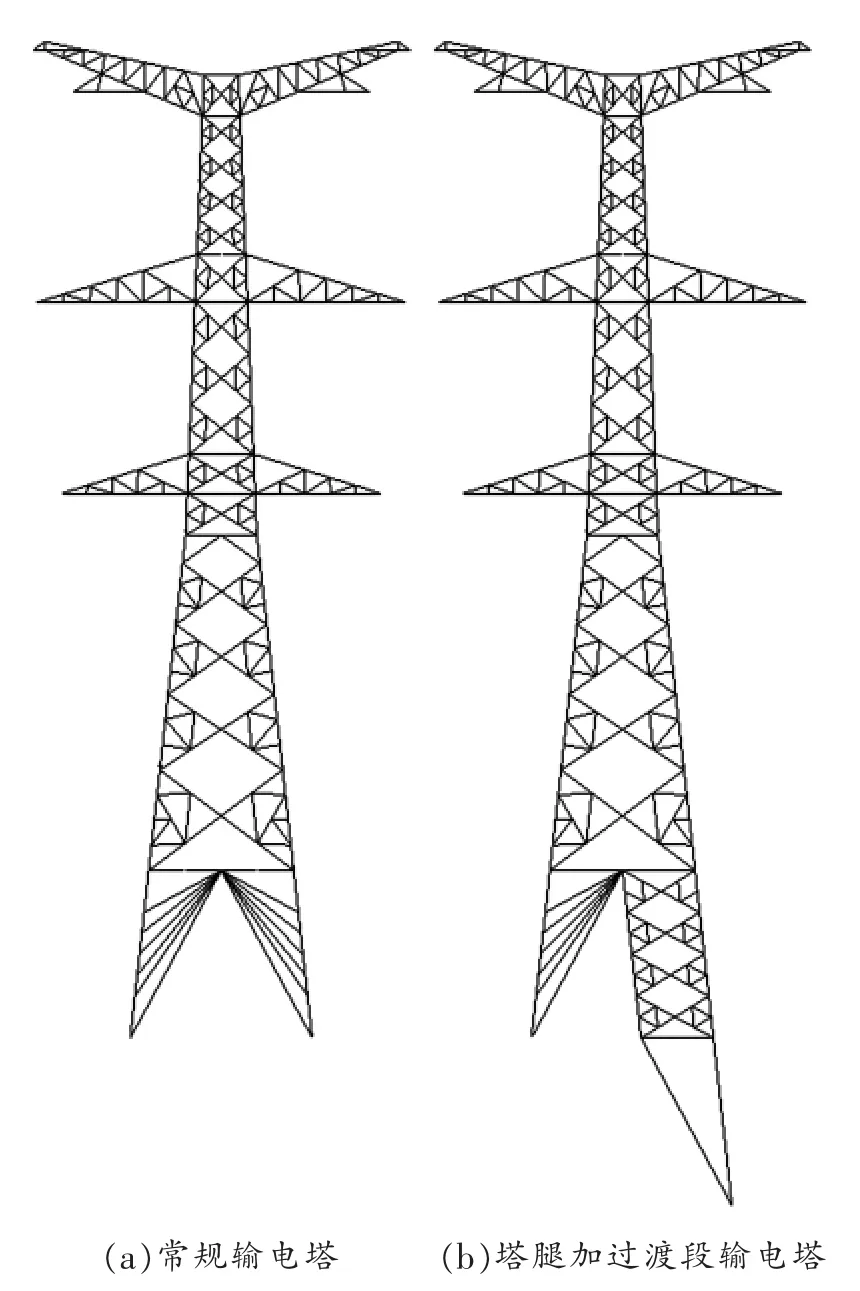
图1 SZC4直线塔

SZC4直线塔高71.35 m，呼高39 m，塔头高32.35 m，全塔杆件为角钢。根据GB50260—2013《电力设施抗震设计规范》［7］8.2.1条，计算杆塔动力特性时，可不计入导线和避雷线的重量。邓洪洲等人研究表明［8］，地震作用下导地线产生的摆动会消耗一部分的能量，能够起到阻尼器的作用，塔线体系的地震响应小于单塔，导地线对输电塔抗震是有利的。分析时可选用单塔的简化模型［9-11］。

分析选用5个单塔空间有限元模型，其塔腿隔面以上部分完全相同，仅塔腿不同。常规输电塔和塔腿加过渡段输电塔立面见图1，模型描述见表1。其中，模型II和模型Ⅲ属于含1个最长腿的情况（情况1），模型IV和模型V属于含2个最长腿的情况（情况2）。4个高低腿模型的塔腿编号和塔腿分布如图2所示。

表1 5个模型描述

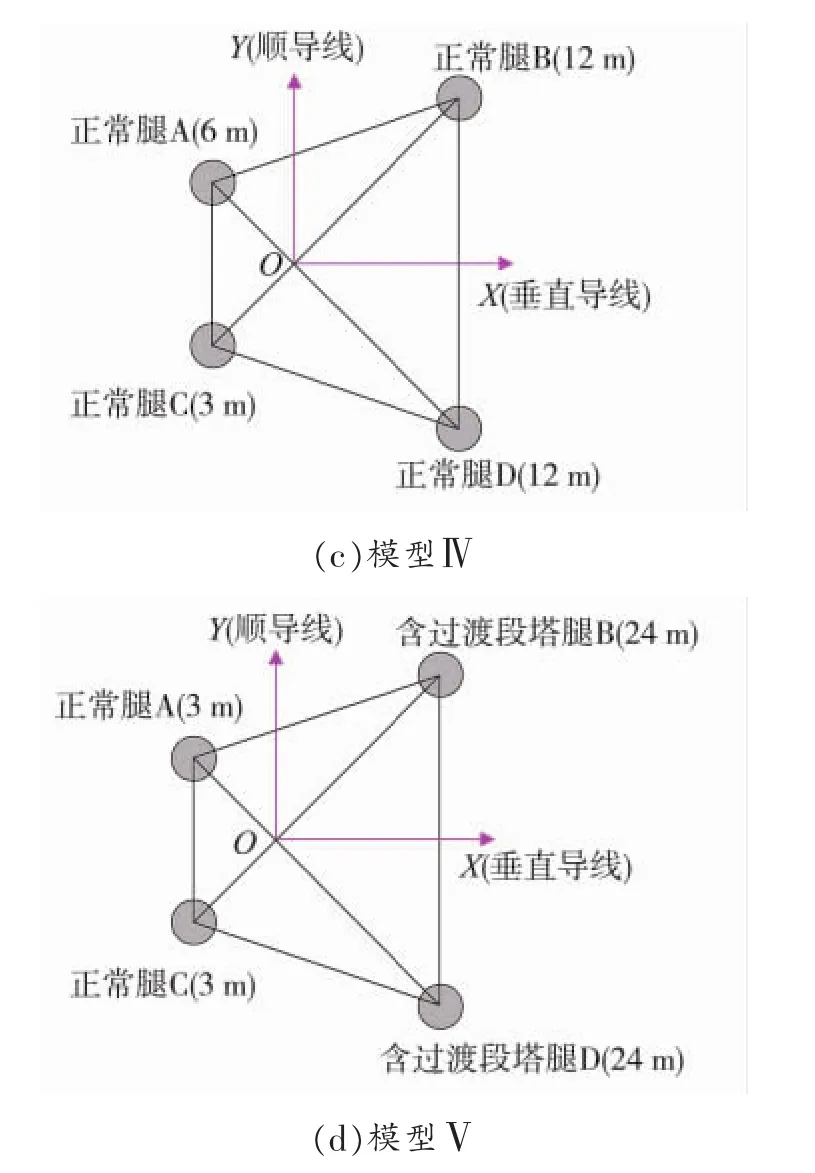
图2 4个高低腿SZC4直线塔模型的塔腿分布

2 动力特性

表2～6分别给出了5个模型的低阶自振频率和振型。

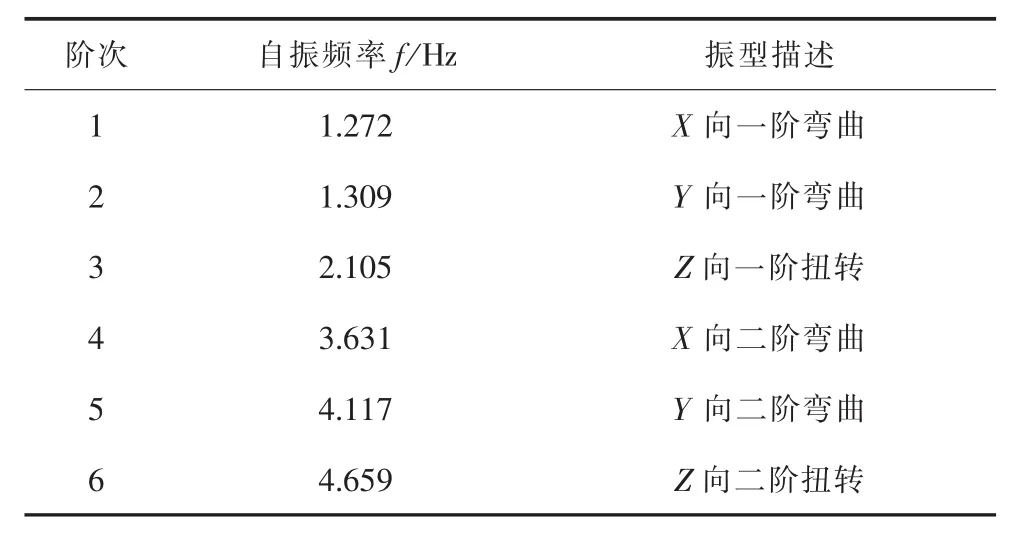
表2 模型Ⅰ的前6阶自振频率和振型

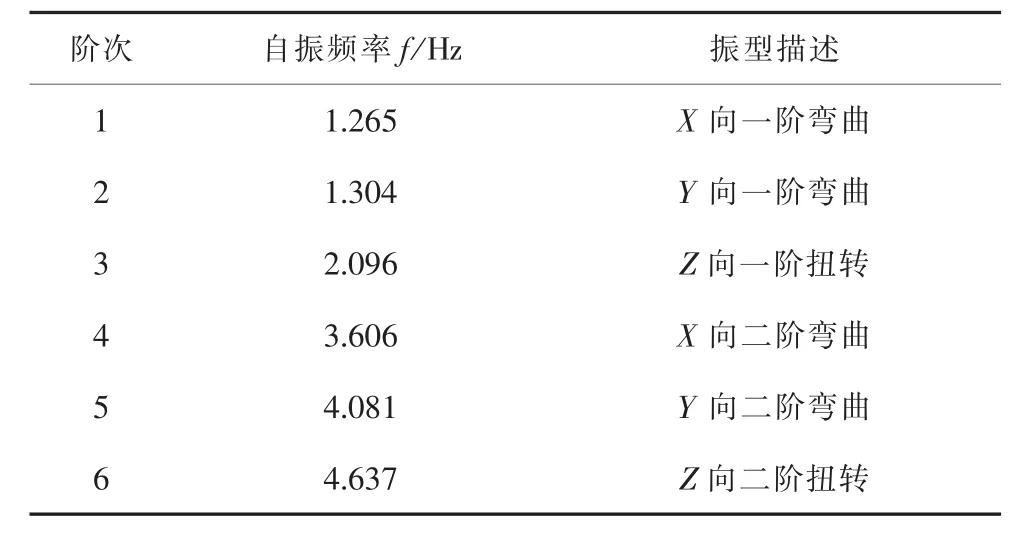
表3 模型Ⅱ的前6阶自振频率和振型

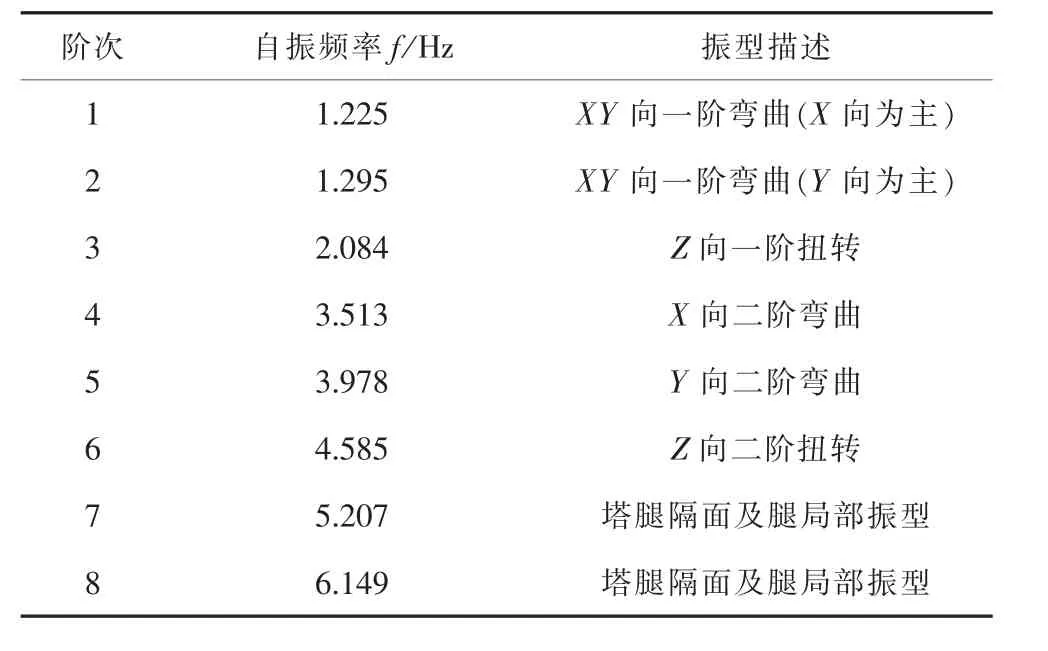
表4 模型Ⅲ的前8阶自振频率和振型

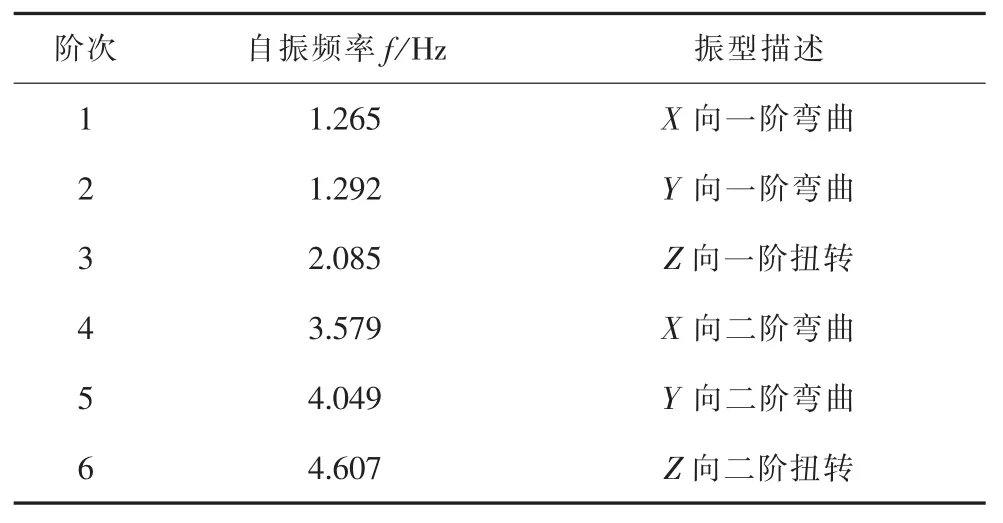
表5 模型Ⅳ的前6阶自振频率和振型

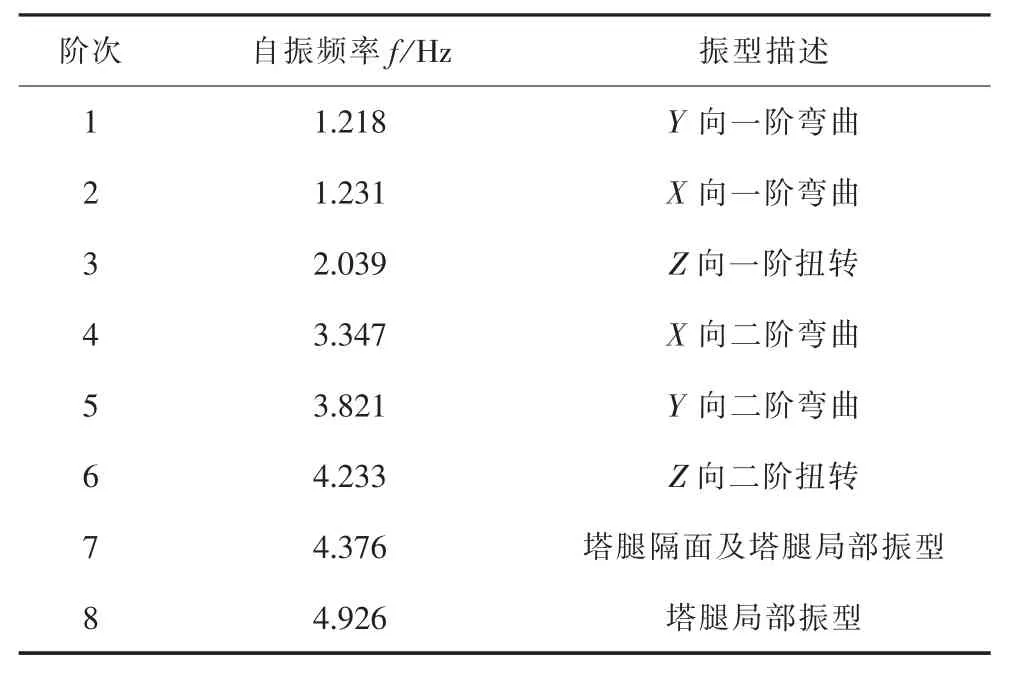
表6 模型Ⅴ的前8阶自振频率和振型

可以看出，平腿模型I的振型特点符合此类塔型的振型特点［12］，第 1～2 阶（塔的一阶弯曲振型）为X、Y两个方向的弯曲振型，两个方向的频率值非常接近，相差2.9%，这是由于两个方向的刚度相近，仅横担的质量分布稍有差异；第3阶为扭转振型，为一阶弯曲振型的1.66倍，也符合此塔型的振型分布特点；第4～5阶振型（塔的二阶弯曲振型）也为X、Y两个方向的弯曲振型；第6阶为扭转振型。

情况1下的常规高低腿模型Ⅱ的振型分布与平腿模型完全一致，第1阶频率值低0.50%，表明对于通常工程中常规高低腿设计时输电塔的动力特性不需要另做分析计算，只需用平腿模型分析即可。但塔腿加过渡段高低腿模型Ⅲ的1～2阶振型 （塔的一阶弯曲振型）已不是单一方向（X或Y）的振动，而是变成了第1阶振型以X向为主、同时也有Y向振型参与，第2阶振型变成了以Y向为主、同时也有X向振型参与，这是因为塔腿高差太大，刚度沿X、Y轴不对称；第1阶频率值较常规高低腿降低3.2%；第3阶振型为扭转振型，较常规高低腿降低0.56%；第4～5阶振型（塔的二阶弯曲振型）为X、Y两个方向的弯曲振型；第6阶为扭转振型；第7～8阶振型为腿隔面及腿局部振型。

情况2下的常规高低腿模型Ⅳ的振型分布与平腿模型完全一致，第1阶频率值低0.51%，表明对于通常工程中常规高低腿设计时输电塔的动力特性不需要另做分析计算，只需用平腿模型分析即可。但塔腿加过渡段高低腿模型Ⅴ的第1～2阶振型 （塔的一阶弯曲振型）和常规高低腿模型方向相反。这是因为塔腿高差太大，刚度沿X轴不对称；第1阶频率值较常规高低腿降低3.7%；第3阶振型为扭转振型，较常规高低腿降低2.2%；第4～5阶振型（塔的二阶弯曲振型）为X、Y两个方向的弯曲振型；第6阶为扭转振型；第7～8阶振型为腿隔面及腿局部振型。

综上，塔腿加过渡段高低腿铁塔的前6阶振型分布变化不大，对动力响应影响有限。但由于塔的对称性变差，导致一阶弯曲振型方向发生变化。

3 单向地震作用下的时程响应

分析对象位于四川省阿坝州茂县—松潘地区，场地分组为第一组，场地类别为Ⅱ类场地，特征周期0.35 s［13］。根据 GB50135—2006《高耸结构设计规范》［14］4.4.7 节规定，钢结构铁塔阻尼比取 0.02。

地震峰值加速度选用9度设防烈度0.4g，对所选用的地震波加速度时程峰值进行调幅。

选取EL-CENTRO波（EL波），按要求进行峰值调幅后，地震波的加速度时程如图3所示。

3.1 X向（垂直导线）地震作用下的时程响应

5个单塔模型在X向（垂直导线）地震下的塔顶位移响应如图4～8所示。表7给出了5个模型在X向地震下塔顶位移响应峰值。

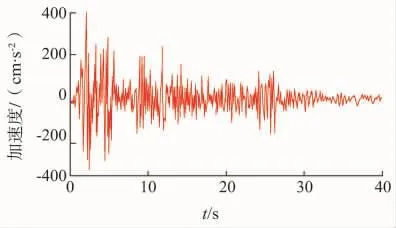
图3 EL-CENTRO波调幅后的加速度时程曲线

图4 EL-CENTRO波X向输入下模型I塔顶位移响应

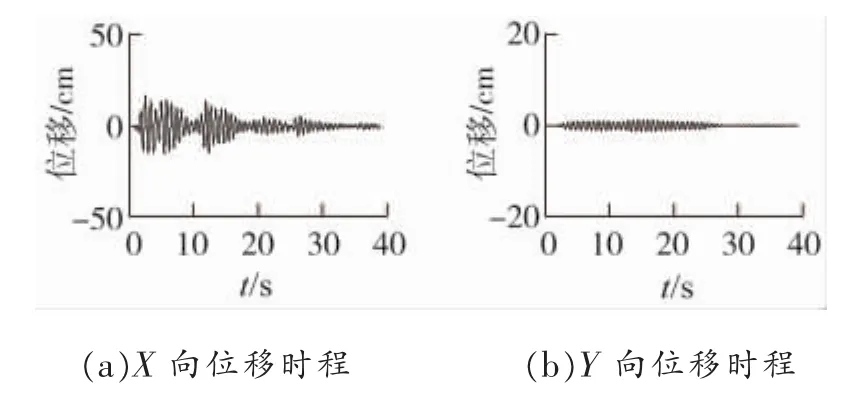
图5 EL-CENTRO波X向输入下模型II塔顶位移响应

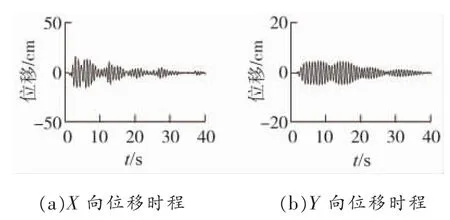
图6 EL-CENTRO波X向输入下模型Ⅲ塔顶位移响应

图7 EL-CENTRO波X向输入下模型IV塔顶位移响应

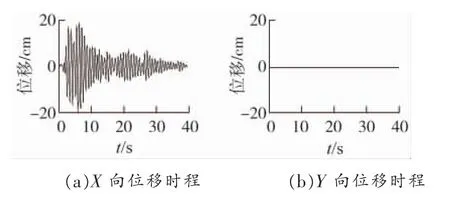
图8 EL-CENTRO波X向输入下模型V塔顶位移响应

表7 EL-CENTRO波X向输入下塔顶位移响应峰值

可以看出，平腿模型Ⅰ由于X、Y向对称性较好，因此在X向地震下，位移响应以X向为主，达到了16.4 cm，而Y向位移非常小，为0.013 cm，是X向位移的0.08%，符合常规平腿塔的特性［15］，X向与Y向之间没有耦合性。

情况1中，由于高低腿导致整塔X、Y向都不对称，因此X向地震下会引起Y向较大响应。常规高低腿模型Ⅱ在X向地震下Y向位移响应达到了X向8.15%，而塔腿加过渡段高低腿模型Ⅲ在X向地震下Y向位移响应更是达到了X向30.15%，对称性大大下降。

情况2中，虽然高低腿导致整塔X向变得不对称，但Y向依然具有对称性，因此在X向地震下Y向位移响应也非常小。不过此情况下模型的X向位移响应比平腿模型有较明显增加，模型V的X向位移响应比模型I增加了21%左右。

3.2 Y向（顺导线）地震作用下的时程响应

5个单塔模型在Y向（顺导线）地震下的塔顶位移响应如图9～13所示。表8给出了5个模型在Y向地震下塔顶位移响应峰值。

可以看出，平腿模型Ⅰ由于X、Y向对称性较好，因此在Y向地震下，位移响应以Y向为主，达到了16.5 cm，而X向位移非常小，为0.020 cm，是Y向位移的0.12%，符合常规平腿塔的特性，X向与Y向之间没有耦合性。

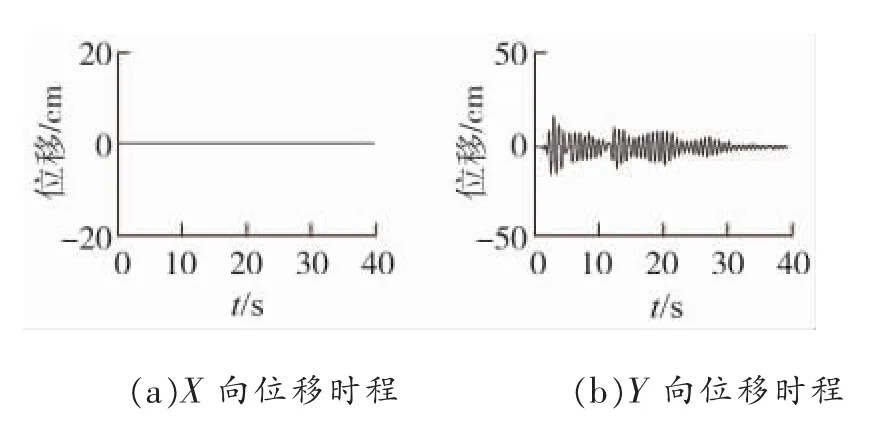
图9 EL-CENTRO波Y向输入下模型I塔顶位移响应

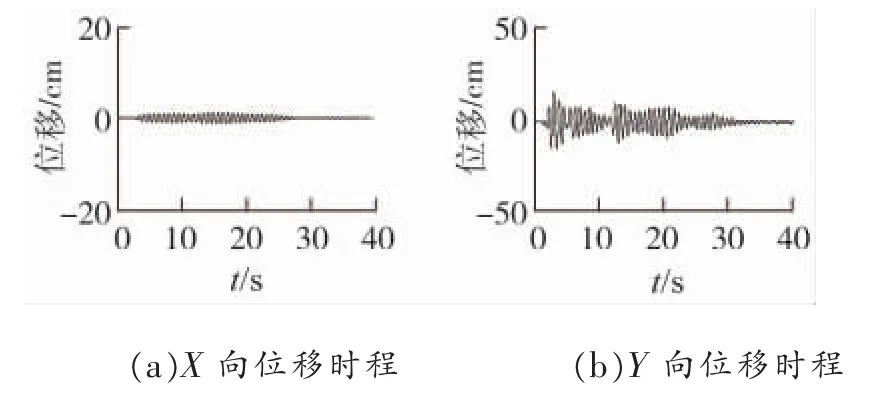
图10 EL-CENTRO波Y向输入下模型II塔顶位移响应

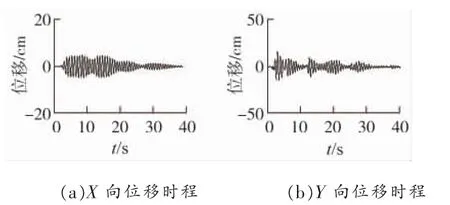
图11 EL-CENTRO波Y向输入下模型Ⅲ塔顶位移响应

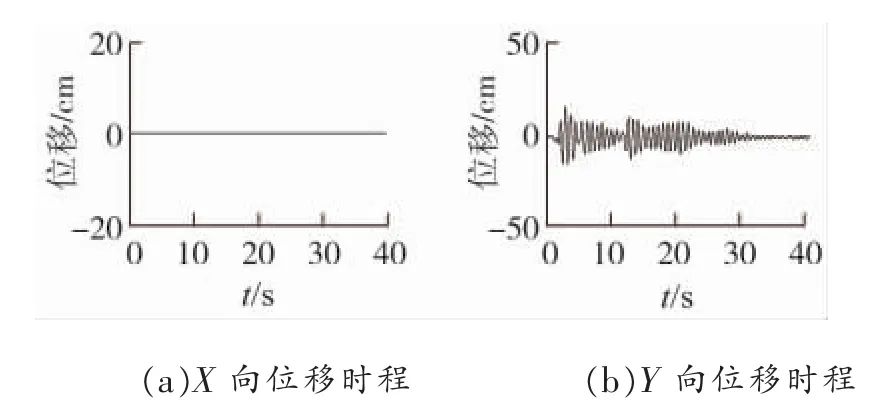
图12 EL-CENTRO波Y向输入下模型IV塔顶位移响应

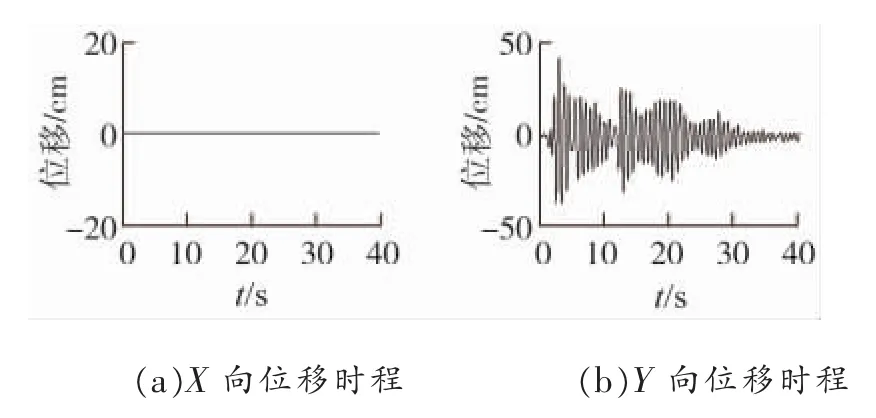
图13 EL-CENTRO波Y向输入下模型V塔顶位移响应

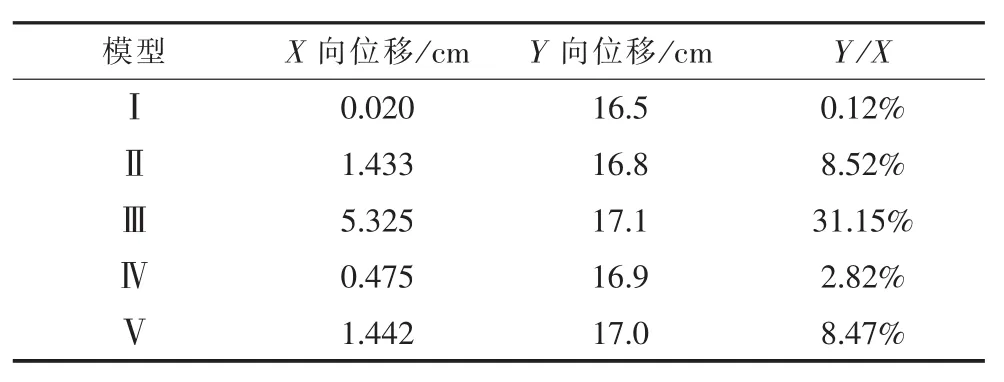
表8 EL-CENTRO波Y向输入下塔顶位移响应峰值

情况1中，由于高低腿导致整塔X、Y向都不对称，因此Y向地震下会引起X向较大响应。常规高低腿模型Ⅱ在Y向地震下X向位移响应达到了Y向8.52%，而塔腿加过渡段高低腿模型Ⅲ在Y向地震下X向位移响应更是达到了Y向31.15%，对称性大大下降。

情况2中，高低腿导致整塔X向变得不对称，Y向依然具有对称性，在Y向地震下X向位移响应占比有所增加，常规高低腿模型Ⅳ在Y向地震下X向位移响应达到了Y向2.82%，而塔腿加过渡段高低腿模型V在Y向地震下X向位移响达到了Y向8.47%，对称性下降。

4三向地震作用下的时程响应

对5个模型分别进行三向地震波输入，X，Y，Z 3个方向的加速度最大值按照1∶0.85∶0.65的比例调整。地震时程计算结果如图14～19所示。表9给出了5个模型在三向地震下结构位移响应峰值。

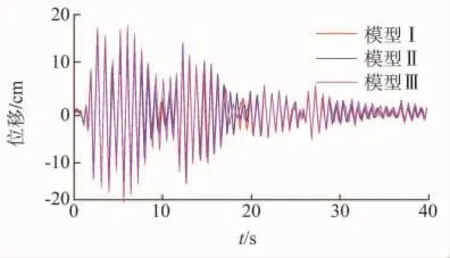
图14 SZC4直线塔模型Ⅰ，Ⅱ，Ⅲ的塔顶X向位移时程

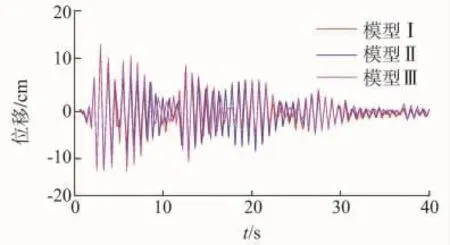
图15 SZC4直线塔模型Ⅰ，Ⅱ，Ⅲ的塔顶Y向位移时程

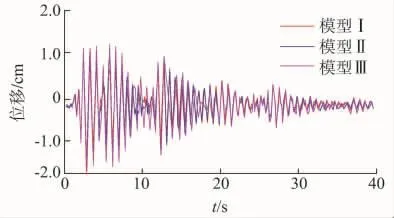
图16 SZC4直线塔模型Ⅰ，Ⅱ，Ⅲ的塔顶Z向位移曲线

由图14～16可以看出，情况1的模型II和模型Ⅲ在地震作用下三向位移的时程曲线形状与平腿模型I大致相同，只是峰值略有差别。

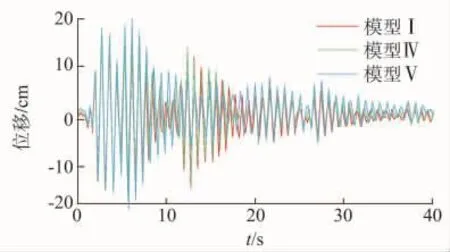
图17 直线塔SZC4模型Ⅰ，Ⅳ，Ⅴ的塔顶X向位移曲线

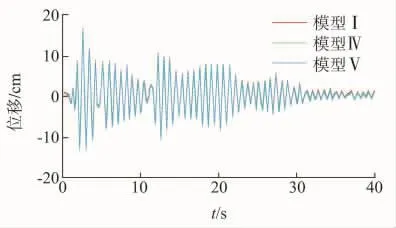
图18 直线塔SZC4模型Ⅰ，Ⅳ，Ⅴ的塔顶Y向位移曲线

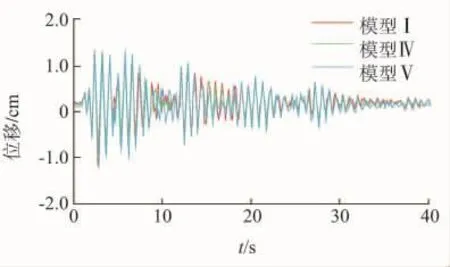
图19 直线塔SZC4模型Ⅰ，Ⅳ，Ⅴ的塔顶Z向位移曲线

由图17～19可以看出，情况2的模型Ⅳ和模型Ⅴ在地震作用下三向位移的时程曲线形状与平腿模型I大致相同，只是峰值略有差别。

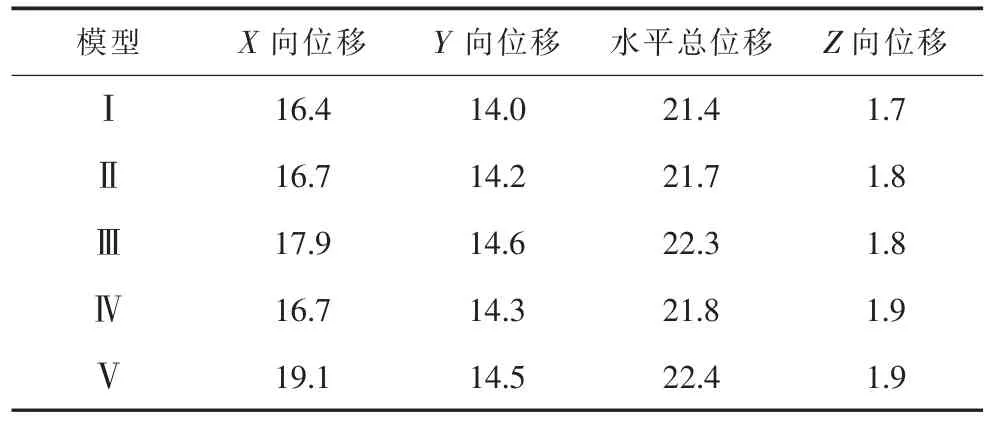
表9 SZC4在EL-CENTRO波三向输入时结构位移响应峰值 cm

由表9可以看出，无论是平腿模型还是高低腿模型，Z向的位移与X，Y向的位移相比都很小；高低腿整塔模型在地震作用下，塔顶的三向位移与平腿模型Ⅰ相比均有所增大；塔腿加过渡段高低腿模型Ⅲ和模型Ⅴ与常规高低腿模型Ⅱ和模型Ⅳ相比增大的幅度较大；X向位移的变化幅度较大。

其中，模型Ⅴ的X向位移比模型Ⅰ增大了16.7%；模型Ⅲ的Y向位移比模型Ⅰ增大了3.7%；模型Ⅴ的Z向位移比模型Ⅰ增大了11.2%。

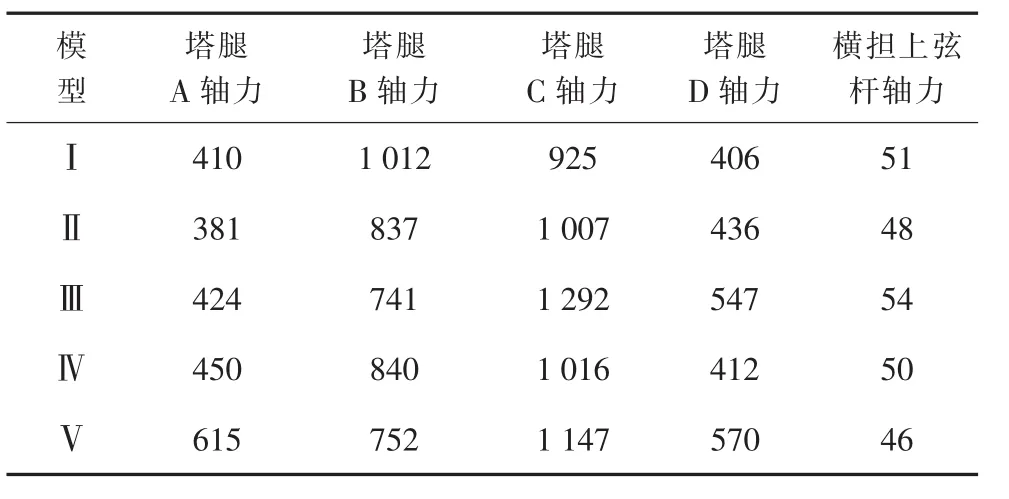
表10 SZC4在EL-CENTRO波三向输入时杆件内力响应峰值 kN

由表10可以看出，塔腿加过渡段高低腿模型Ⅲ和模型V在三向地震作用下，塔腿的最大轴力跟平腿模型I相比都增大了，其中最大增幅出现在模型Ⅲ上，达到了28%。但此时的地震力为1 292 kN，而塔腿主材L250×24D（Q420）的设计允许轴力为3 600 kN左右，是地震力的2.7倍。

横担上弦杆的轴力，尽管不同的模型在地震作用下有大有小，模型Ⅲ比模型I增大了6.9%，但横担上弦杆L180×12D（Q420）的设计允许轴力为940 kN左右，远大于地震作用下的轴力。

可见，对塔腿增加过渡段后，主要在塔腿处产生附加应力，但地震力远小于设计允许值，此时连接4根主材的横隔面成为重要结构，应进行适当加强。

5 结语

高低腿铁塔的自振频率与平腿铁塔相比有所降低，塔腿加过渡段铁塔自振频率降低幅度比常规高低腿铁塔大。

塔腿加过渡段铁塔的前6阶振型分布变化不大，对动力响应影响有限。但由于塔的对称性变差，导致一阶弯曲振型方向发生变化。

由于塔腿加过渡段高低腿铁塔的对称性变差，单向地震下会导致垂直于地震作用方向的位移响应变大。

三向地震作用下，常规高低腿模型的位移响应峰值和内力响应峰值与平腿模型的响应峰值差别很小，仅略微增大；塔腿加过渡段高低腿模型的位移响应峰值和内力响应峰值则与平腿模型的响应峰值相比有较明显增大。

三向地震作用下，模型Ⅴ（含有2个塔腿过渡段）的X向最大位移比模型Ⅰ（平腿）增大了16.7%；模型Ⅲ（含有1个塔腿过渡段）的Y向最大位移比模型Ⅰ增大了3.7%；模型Ⅴ的Z向最大位移比模型I增大了11.2%；含有过渡段的模型Ⅲ和模型Ⅴ在三向地震作用下，塔腿的最大轴力跟平腿情况的模型I相比都增大了，其中最大增幅出现在模型Ⅲ上，达到了28%；横担上弦杆的最大轴力，模型Ⅲ比模型I增大了6.9%。

塔腿加过渡段高低腿模型在三向地震下的某些杆件内力峰值有所增大，但与杆件的设计允许内力相比，最大地震力也只占到设计轴力36%，荷载组合后不会超出整塔的承载能力，地震效应不起主要控制作用。

塔腿增加过渡段后，导致铁塔的竖向刚度变得不均匀，连接4根主材的横隔面成为薄弱环节，高烈度地震设防设计时应对塔腿处及塔身的横隔面进行加强处理。