SINS/GPS组合导航系统Kalman滤波仿真研究

王艳梅,王海生

(沈阳理工大学 自动化与电气工程学院,沈阳 110159)

捷联惯导系统(Strapdown Inertial Navigation System,SINS)是一种真正意义上的自主式导航系统,其自主地提供运载体的加速度、速度、位置和角速度、姿态等信息,不需要向外界发射任何信息,完全依靠机械设备自主地完成导航任务[1],但其缺点是误差会随着时间不断地积累,长期运行精度差。

全球定位系统(Global Positioning System,GPS)是由美国国防部研制建立的一种具有全方位、全天候、全时段、高精度的卫星导航系统[2],能提供高精度的三维位置、速度和精确定时等导航信息,但其存在信号易受遮挡或干扰、动态性能差等缺陷。

SINS/GPS组合导航系统利用SINS与GPS良好的优势互补性,把两种导航系统合理地组合在一起,可以提高导航系统的整体精度和可靠性[3],较好地弥补单一系统在导航性能上的缺陷。本文同时考虑SINS和GPS的臂杆误差和时间不同步误差,把组合系统状态向量由15维增加到19维,并进行滤波仿真,研究组合导航对定位精度的影响。

1 SINS和GPS原理

1.1 捷联惯导原理

选取东北天坐标系为导航坐标系,捷联惯性导航系统原理如图1所示。

图1 捷联惯性导航系统原理图

陀螺仪和加速度计固联在载体上,分别测量载体的角运动和线运动信息[4];导航计算机由这些测量信息推算出载体的姿态、航向、速度和位置。

SINS速度、位置、姿态更新计算公式[5]如式(1)～式(3)所示。

速度更新

(1)

位置更新

(2)

姿态更新

(3)

1.2 GPS定位原理

GPS卫星定位系统定位的基本原理是延时测距,通过测量四个已知位置上信号传播的延迟时间,确定四个已知位置至用户的距离,根据这四个量测距离解算出用户的三维位置和用户与已知位置的同步偏差。

由卫星星历可计算得到卫星速度、位置,再由轨迹仿真得到接收机的速度和位置,把卫星和接收机的速度、位置结合得到理论的星地距离和其变化率,再计入GPS各种误差,推出近似真实的GPS原始观测数据。对GPS原始观测数据进行导航解算,仿真出GPS输出结果。在实际仿真中,GPS接收机钟差、接收机噪声、星钟等效距离误差等可影响GPS定位参数的精确度[6]。

2 扩展Kalman滤波EKF算法

常规Kalman滤波KF主要处理线性数学模型,对于非线性模型不适用[7],可采用扩展Kalman滤波器EKF对非线性系统进行处理;把非线性系统用Tylor级数处理转化成线性系统[8],再用KF完成状态的估计。

EKF滤波算法的基本方程为

(4)

3 SINS/GPS组合导航

3.1 SINS/GPS组合导航原理

SINS/GPS组合导航技术,是目前最先进的、全天候、自主式导航技术,有广泛应用前景[9]。最优估计理论数据处理方法的发展为组合导航提供了有力的理论依据[10]。

图2是应用Kalman滤波器设计组合导航系统的原理图。

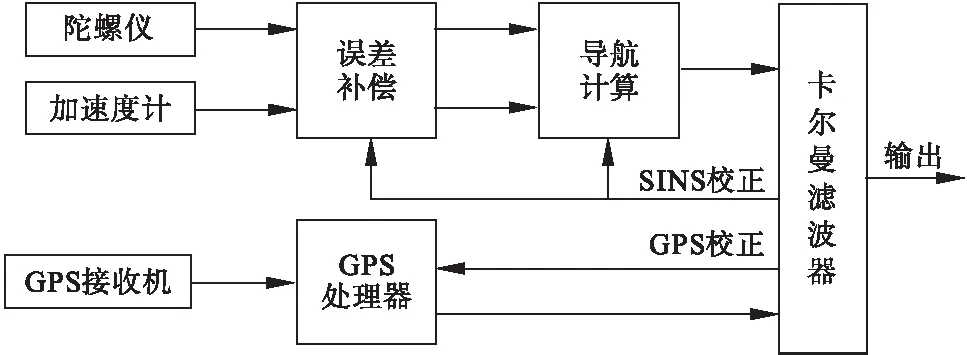
图2 SINS/GPS组合导航原理图

先建立以SINS误差方程为基础的组合导航系统的状态方程,在其基础上再建立导航系统的测量方程。这两个方程是时变、线性的,用线性Kalman滤波器对SINS提供最小方差估计,然后用误差的估计值去修正SINS,达到减少导航误差的目的;校正后的SINS又能提供导航信息,辅助GPS提高其性能和可靠性。

3.2 SINS和GPS空间杆臂误差

SINS通常将惯性测量单元(IMU)的几何中心当做导航定位或测速的参考基准;而GPS将接收机天线的相位中心当做参考基准;把二者进行组合时,在安装位置上往往会产生一定的偏差,如图3所示。

假设IMU相对于地心Oe的矢量为R,GPS接收机天线相位中心相对于地心的矢量为r,天线相位中心相对于IMU的矢量为δl,三者之间的矢量关系为

r=R+δl

(5)

图3 IMU与卫星接收机天线之间的杆臂

杆臂δl在载体坐标系(b系)下为常矢量,式(5)两边相对地球直角坐标系(e系)求导得

(6)

(7)

SINS和GPS之间杆臂位置误差δpSG为

(8)

3.3 SINS和GPS时间不同步误差

在SINS/GPS组合系统中,导航计算机获取不同传感器的信息都存在一定的时间滞后,而且不同传感器的时间滞后一般不同步,图4是IMU与GPS接收机的时间不同步示意图。

设IMU与GPS接收机的时间不同步误差为δt,二者组合时,必须对δt进行估计和补偿。SINS与GPS速度之间的关系为

(9)

式中an是载体在不同步时间内的平均线加速度。则SINS与GPS的速度和位置不同步的误差分别为

(10)

(11)

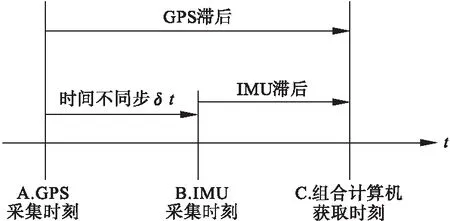
图4 IMU与GPS接收机的时间不同步

3.4 SINS/GPS组合导航系统模型

在SINS误差分析的基础上,同时考虑SINS和GPS的杆臂误差和时间不同步误差,建立以速度和位置误差为观测量的SINS/GPS组合导航状态空间模型。

(12)

式中:X为系统的状态向量;F为系统的状态矩阵;G为系统的动态噪声矩阵;Wb为系统的过程白噪声矢量。

本文系统状态向量选取19维,过程白噪声矢量为6维,量测噪声矢量为6维。

X=[φT(δvn)T(δp)T(εb)T(▽b)T(δlb)Tδt]T

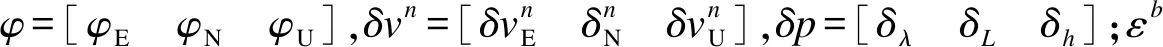
由SINS和GPS的速度误差、位置误差组合模式得到系统的观测方程为

(13)

式中：Z为系统的量测矢量;H为系统的量测矩阵;V为系统的量测噪声矢量。

4 SINS/GPS组合导航仿真与分析

以东、北、天坐标系为导航坐标系,模拟运载体的运动轨迹,设东、北、天方向的初始平台误差角分别为20″、-25″和20″,初始速度误差为∂vn=[0.1 0.1 0.1],初始位置误差为δp=[2 2 2],设陀螺仪的常值漂移为0.05°/h,加速度计的常值漂移100μg,初始臂杆误差δl=[1 2 3],初始时间不同步误差δt=0.1s,设采样周期ΔTsamp=0.1s,设GPS的速度、位置定位误差分别为3m/s和10m,GPS和组合导航的输出频率都为10Hz。把仿真运载体产生的运动轨迹的值与GPS接收机的定义误差相加,得到GPS的定位信息,仿真时间1000s,仿真结果如图5～图11所示。

图5是Matlab仿真运载体的运动轨迹。

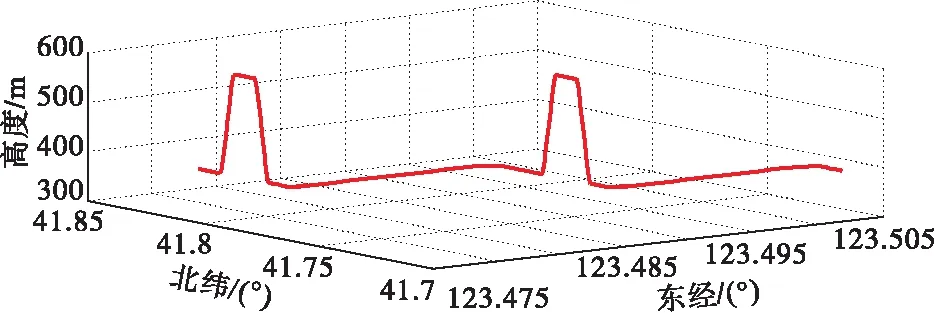
图5 仿真运载体的运动轨迹

图5中运载体以东经123.51°、北纬41.72°、高度300m位置作为起始点运动,运动形态有加速运动、匀速运动、减速运动、爬高运动、转弯运动、下降运动等多种常规的运动状态,运动轨迹为SINS/GPS组合导航仿真追踪使用。

图6～图8中虚线表示高度误差,实线表示纬度误差,点虚线表示经度误差。

图6是SINS单独工作的东、北、天方向的位置误差变化曲线。

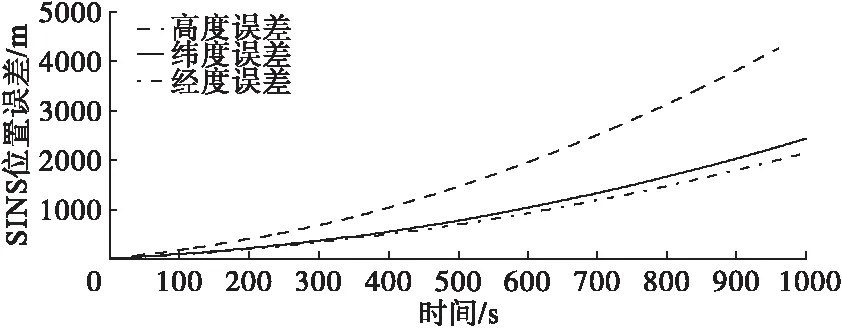
图6 SINS东、北、天方向位置误差曲线

由图6可知,随着时间增加,SINS位置误差增加越来越快,在800s时,经度误差达到1200m,纬度误差达到1400m,高度误差达到3000m。

图7是GPS接收机单独工作时东、北、天方向的位置误差变化曲线。

图7 GPS接收机位置误差曲线

由图7可知,GPS接收机各向位置误差不随时间积累,定位精度较高,经度、纬度、高度误差都在20m左右。

图8是经过EKF滤波的SINS/GPS组合的东、北、天方向的位置误差变化曲线。

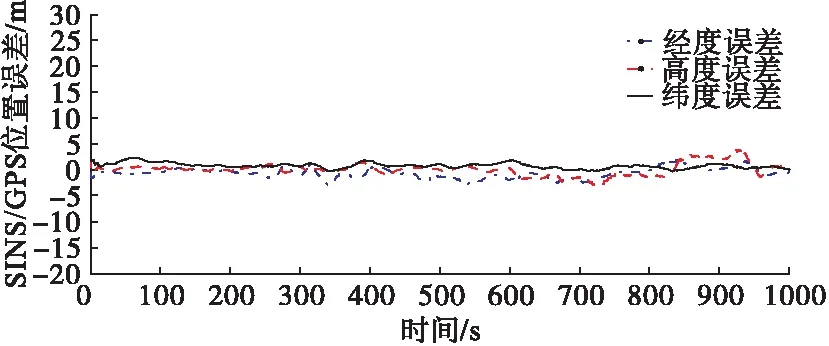
图8 SINS/GPS组合导航位置误差曲线

由图8可知,SINS/GPS组合系统的经度、纬度、高度误差都在2m以内,与SINS、GPS单独工作时的误差相比,位置误差精度大大提高。

图9是SINS单独工作的东、北、天方向的速度误差变化曲线。

由图9可知,随着时间增加,各向速度误差不断增大,特别是天向速度误差发散更快,在800s时达到11m/s。

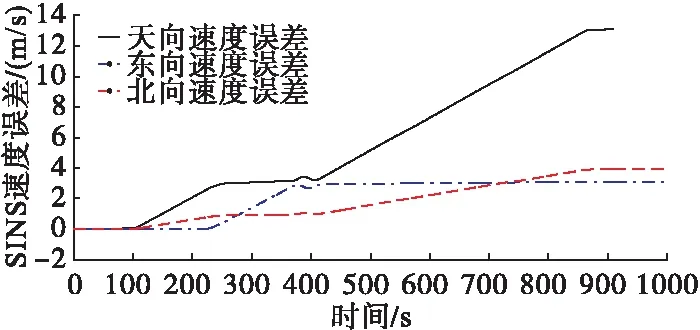
图9 SINS东、北、天方向的速度误差曲线

图10是GPS接收机单独工作的东、北、天方向的速度误差变化曲线。

图10 GPS接收机速度误差曲线

由图10可知,GPS接收的各向速度误差不随时间积累,各向速度误差都在3m/s左右。

图11是经过EKF滤波的SINS/GPS组合的东、北、天方向的速度误差变化曲线。

图11 SINS/GPS组合导航速度误差曲线

由图11可知,SINS/GPS组合系统的各向速度误差都在0.5m/s以内,与SINS、GPS单独工作时的速度误差相比,误差精度大大提高。

综上,SINS单独工作时,在100s内速度、位置误差都比GPS单独工作时小很多,但随着时间增加,误差积累越来越大。GPS接收机定位精度较高,但GPS易受干扰。SINS/GPS组合系统兼具SINS和GPS各自的优势,经过EKF信息融合后,导航精度大大提高,证明所建立的模型是正确的。

5 结论

在传统的SINS/GPS组合导航系统的基础上,加入了SINS和GPS之间的杆臂误差和时间不同步误差,把系统的状态向量由15维增加到19维,并用扩展Kalman滤波EKF算法对SINS/GPS组合系统进行滤波仿真。Matlab仿真结果表明,SINS/GPS组合系统可以有效地去除SINS的长期精度差、GPS易受干扰的缺点,提高导航精度,说明这种组合可行。