改进样本熵最优小波包阈值选择算法在信号降噪中的应用

何 勇，张祥金，姚宗辰

(南京理工大学 机械工程学院， 南京 210094)

在信号降噪处理中小波包阈值的选择显得尤为重要，传统的阈值估计方法如软阈值、硬阈值等在信噪比较高时能得到信号与噪声的最优分离，而对于受噪声污染严重的信号，其去噪效果往往不甚理想[1]。罗元[2]提出基于Teager能量算子的改进阈值函数去噪算法；康玉梅[3]提出了小波包分数幂阈值的新方法；刘冲冲[4]提出了一种基于自适应阈值和新阈值函数的小波包语音增强算法；周建[5]利用样本熵作为信息价值函数以确定最优小波包，且以样本熵为判据，对不同的分解层数设置不同的阈值，选取使得去噪后得到的噪声信号样本熵值最大的阈值作为最优阈值，并且与传统阈值选择进行了比较分析。

文献[5]给出了小波包样本熵最优阈值选择原理，但是没有考虑阈值步长大小对样本熵曲线的影响，也没有详细说明怎样设置阈值步长。本文在此基础上，分析了初始阈值以及阈值增加步长的大小对噪声序列样本熵产生的影响。为了改进算法，提出将阈值作为变量，阈值步长作为新的环境特征，构造目标函数，结合粒子群动态优化算法估计小波包最优阈值。

1 相关理论

1.1 小波包理论

小波包分解是在全频带内对信号进行多分辨率分解系数的分析方法。设采样到的离散数据为{X(k)}k=1,2,…,N，对其进行小波包的分解，分解算法[6]为

(1)

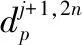
(2)

1.2 样本熵理论

样本熵反映时间序列的复杂度与无规律程度，样本熵值越小，则时间序列的自相似度越高，序列越规则; 熵值越大，表示序列越为复杂，取值也更加随机[7]。

设有时间序列为Xi={x1,x2,…,xN},长度为N,则样本熵计算如下。

① 设定嵌入维数为m和相似容限r,考虑维数为m的向量组{xm(1),…,xm(N-m-1)},其中：

Xm(i)={x(i),x(i+1),…,x(i+m-1)}

1≤i≤N-m+1

(3)

② 设两个向量Xm(i)和Xm(j)之间距离d[Xm(i),Xm(j)]为向量之间对应元素之差绝对值的最大值。则有：

(4)

③ 设定固定的Xm(i),对Xm(i)与Xm(j)之间的距离小于等于相似容限r的j(1≤i≤N-m，j≠i)的数目进行统计，并记作Bi。则当1≤i≤N-m时，定义：

④ 设B(m)(r)为：

(5)

⑤ 将嵌入维数增加到m+1，按照上述计算Xm+1(i)与之间距离小于等于r的个数，并记作Ai。则有：

(6)

⑥ 同样地

(7)

由以上计算分析可知，B(m)(r) 是两个向量在相似容限r下匹配m个点的概率，而Am(r) 是两个向量匹配m+1个点的概率。则定义该时间序列的样本熵为:

(8)

实际信号中N通常为有限值，样本熵可以估计为:

(9)

一般r=0.1Std～0.25Std(Std为时间序列Xi={x1，x2，…，xN} 的标准差),取m=1或2。在本文的分析中，取m=2，r=0.2Std。

1.3 动态粒子群优化算法

粒子群算法，也称粒子群优化算法或鸟群觅食算法(PSO)。PSO算法从随机解出发，通过追随当前搜索到的最优值来寻找全局最优，以适应度来评价解的品质。

系统初始化为一组随机解，通过迭代搜寻最优值，粒子在解空间追随最优的粒子进行搜索。粒子速度公式为[8]：

vid(t+1)=ω*vid(t)+c1r1(pid-xid(t))+

c2r2(pgd-xid(t))

(10)

位置更新公式：

xid(t+1)=xid(t)+vid(t+1)

(11)

式(10)～式(11)中：vid(t)，xid(t)分别表示t时刻粒子i的飞行速度和位置；pid表示粒子i的个体历史最佳位置；pgd表示群体中最佳位置；ω表示惯性权重；c1和c2表示加速因子；r1和r2表示在[0,1]范围内的随机数。

实际问题中，有些目标函数和约束条件也会随着变量的变化而变化，最终导致其问题的最优解改变，是一个动态优化问题，采用改进的粒子群优化算法。种群不随算法迭代而变化，而目标函数和约束函数会随变量改变而改变，那么求解的问题也改变了。因此引入环境检测算子，检测环境变化计算公式为[9]：

(12)

式(12)中，n为重新评价个体的数目，一般为种群大小的10%；fj(x,t-1)为环境变化前的适应值；fj(x,t) 为环境变化后的适应值。对计算结果ε(t)进行如下分类

(13)

式(13)中,ε1为剧烈强度变化的分界点；ε2为中等程度分界点，通常10-3<ε2≤10-2。若ε(t)>ε1，为剧烈的环境变化，此时环境变化强度较大，最优值及其位置将会偏离原始值；当ε2<ε(t)≤ε1，认为是中等强度的环境变化，最优解及其位置应该在原始值附近波动。

2 粒子群动态优化算法的样本熵最优小波包阈值选择原理

目前，已经获取了某炮弹脉冲激光引信发射过载信号。如图1所示为回收的原始信号。

图1 加速度原始信号时域频谱图

由图1可知，尽管回收系统硬件滤波电路滤除大于5 kHz的信号，但是无法完全滤除内部电子噪声。以该回收的原始过载信号为研究对象，利用改进的小波包阈值选择算法分析降噪过程。

2.1 样本熵最优阈值选择原理

设含噪的原始信号为yn(t),小波包设定阈值重构信号为y(t),消除的噪声信号为n(t)，即有n(t)=yn(t)-y(t)。若小波包阈值选择较小时，重构的信号y(t)中必然含有噪声，而噪声n(t)此时序列较为简单，熵值较低；随着阈值增高，噪声序列变得复杂，熵值增高，当与之增大到n(t)恰好包含所有噪声时，熵值最大；再随着阈值增高，噪声信号n(t)中必包含有效信号(有效信号序列较规则)，熵值会开始降低；当阈值增加到一定值后，此时噪声序列同时包括了噪声和有用信号，此后无论阈值如何增加，样本熵曲线都不会再改变，呈水平线。因此，噪声序列n(t)熵值大体趋势是先增加后减少，一定阈值后，呈水平线。取熵值最大的对应的阈值作为小波包重构最优的阈值。

文献[5]仅从原理上分析样本熵曲线而未考虑阈值步长设置的影响以及噪声序列样本熵曲线在局部的随机性。若按照文献[5]进行阈值选择，初始阈值设定为0，阈值区间为[0,4]。设置不同的阈值步长step，计算不同阈值所对应的噪声序列样本熵。如图2所示。

整体来看，无论阈值步长如何变化，噪声序列的样本熵曲线总体趋势都是先增加后减小。而当阈值增加的步长变化时，最大熵值对应的阈值也在不断变化；阈值步长大，则噪声序列样本熵对应的最优阈值误差就大。图2中阈值步长设置不同时，最优阈值也不同(0.4、0.1或者0.15)，因此无法快速获得最优阈值。

图2 不同步长对应噪声序列样本熵曲线

局部来看，由于噪声的随机性，噪声序列局部样本熵大小排列也变得具有随机性，如图3所示，阈值范围为[0,0.5]的噪声序列样本熵曲线。若阈值步长较小(如0.0005)，虽然样本熵曲线能够在整体上呈现先增后减的趋势，但是局部走势会趋于平缓，有可能会出现多个峰值,甚至由于噪声的随机性，会过早的陷入局部最优解,而且运算代价高。

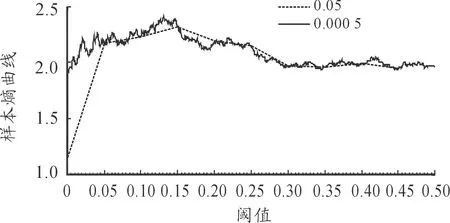
图3 不同步长噪声序列局部样本熵曲线

由图2、图3可以看出，阈值步长的调整是局部与整体的组合关系，本质上是噪声序列的随机性与样本熵规律性的反应。无论步长设置多大，都无法准确快速地找出最大熵值所对应的阈值，且不同的阈值步长，最优小波包阈值也会有所不同。

因此，在样本熵最优小波包阈值估计的理论基础上，提出结合粒子群动态优化算法来确定最优小波包阈值。

2.2 基于粒子群动态算法阈值优化模型

假设噪声序列阈值区间为[ai,bi]，设定阈值步长为step，则阈值序列thr=[ai,…,ai+k*step,…,bi],即有：

thr=g(k;step),k=1,2,3，…,n

(14)

设阈值序列对应重构信号序列y(t)=[yai(t),…,yai+k*step(t),…,ybi(t)],即有：

y(t)=h(thr,t)

(15)

若yn(t)原始信号，则thr对应的噪声序列即有：

n(t)=yn(t)-y(t)

(16)

噪声序列对应的样本熵曲线为

ysamp=Q(n(t))

(17)

而由前面分析，噪声序列样本熵曲线是随着阈值步长的变化而变化的，即目标函数ysamp=Q(n(t))是随着step的变化而变化，目标函数和约束条件也会随着步长的变化而变化，最终导致其问题的最优解改变，当step→0时(step≠0，可以趋于0，否则阈值就不会改变，就是固定阈值)，样本熵序列就会变为样本熵曲线。因此，这是一个动态优化问题，需要增加环境变化因子，该模型中step作为环境变化的因子。一般step初始设置较大，不断减小，以便有较快的收敛速度。

设step=[1,…,0.4,…,0.04,…,0.004,…]是随时间t变化，则有：

step=f(s;t),s=1,2,3,…,n

(18)

结合式(9)、式(14)～式(18),此时，求解最优阈值问题转化为：

max:ysamp=Q(yn(t)-h(g(k;f(s;t)),t))

s.t.ai≤ai+k*step≤bi;

k=1,2,3,…,n；

step=f(t;s)且step≠0；

s=1,2,3,…,n；

其中，ysamp为目标函数,aibi则分别是阈值thr的上下界。

采用改进粒子群算法，在算法迭代过程中根据不同的环境变化采取不同的种群多样性方法。如图4所示，其算法如下：

图4 粒子群动态优化算法

① 建模；将问题空间映射到算法空间，设定相关参数从c1、c2、ω以及粒子数量。

② 初始化种群和最优解存储空间，随机生成群体中粒子候选解的位置和速度。

③ 计算每个粒子对应的适应度值，存储当前粒子最优解，检测粒子的适应度值。

④ 根据式(12)计算step改变前后粒子适应度值的变化ε(t)。比较ε(t)、ε1、ε2；根据实际情况，本文取ε1=0.1、ε2=0.001。

⑤ 若ε(t)>ε1，返回步骤②；若ε2<ε(t)≤ε1，则当前最优解的粒子位置随机生成部分种群，其余粒子重新初始化，返回到③；若ε(t)≤ε2，则更新所有寻优粒子的位置和速度。

⑥ 判断迭代是否完成；若没有完成返回②；若完成则计算结束。

2.3 改进样本熵最优小波包阈值去噪算法原理

由以上分析，对改进样本熵最优小波包阈值的去噪算法如图5所示。

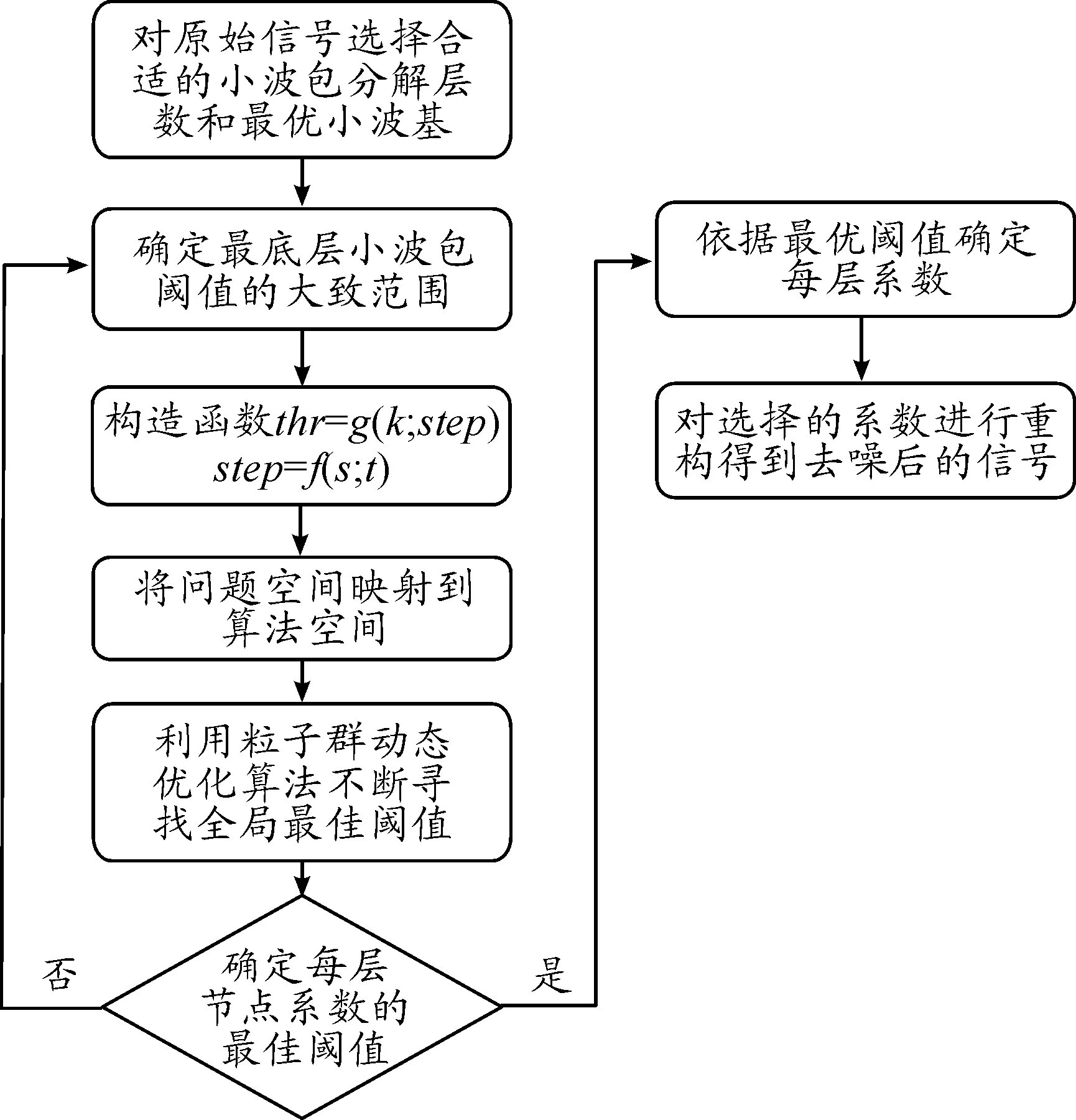
图5 样本熵去噪算法原理

原理如下：

① 对原始信号选择合适的小波包分解层数和最优小波基。

② 对小波包分解的最低层开始，给一个较大阈值步长，计算不同阈值对应的噪声序列样本熵，确定最底层小波包阈值的大致范围thr∈[ai,bi]。

③ 将阈值作为变量，步长作为自变量，构造阈值函数thr=g(k;step)，由于步长是环境变化量，构造步长step随时间变化的函数step=f(s;t)(s=1,2,…)。

④ 建立最优小波包阈值数学模型，将问题空间映射到算法空间，利用粒子群动态优化算法不断寻找全局最佳阈值(噪声序列样本熵最大对应的阈值)。

⑤ 依据②、③、④确定每层节点系数的最佳阈值。

⑥ 每层系数中小于该层最佳阈值的小波包系数置零，大于该层最佳阈值的小波包系数减去阈值后保留下来。

⑦ 对选择的系数进行重构得到去噪后的信号。

3 数据分析与误差评价

为了更好地说明阈值步长设置的影响以及结合粒子群动态优化算法的优越性，同时为了简化计算，对该信号小波包分解的母树即原始信号进行动态优化分析。在算法运行时，阈值步长step=f(s;t)随着一定时间变化，获得的最佳阈值和最佳样本熵也在不断变化。

图6表示分别进行三次算法寻优，步长变化时，最佳阈值的变化轨迹。图6中①为步长开始变化时的最佳阈值，随着步长变化，最佳阈值也开始产生变化，在图6中②出现之前，环境剧烈程度一直为ε(t)>ε1；图6中②表示当步长变为某一值时，此时ε2<ε(t)≤ε1，出现剧烈强度变化的分界点，且从②之后，每次计算都会有不一样的最佳阈值，这是由于随着步长的减小，噪声序列样本熵曲线在局部会显示多个波峰，因此会产生一定的误差；图6中③表示算法运行最终的最优阈值为0.135，在阈值误差≤0.01时，认为在可接受误差范围。没有出现ε(t)≤ε2的环境变化情况。

图6 三次算法运行的最优阈值位置

为了进行误差评价与精度分析，在算法计算过程中选取阈值步长为0.4、0.04、0.004的某一次计算的历史最优值进行评估,如图7、8所示。

图7 历史最佳适应值(样本熵)收敛曲线

图8 历史最佳位置(阈值)收敛曲线

由图7和图8可知，当step=0.4时，开始迭代时就获得了最佳位置和适应值(0.4，1.99)；当step=0.04时，曲线经过14次迭代到达最优值(0.16，2.3)；当step=0.004时，经过88次迭代到达最优值(0.143，3.37)，与算法运行最终的最优阈值(0.135，2.39)相比较，在阈值误差允许范围内(≤0.01)，也可认为此次寻优获得的最佳阈值为0.143。

在未改进算法前，将阈值步长设置为固定值，可能选取固定的阈值步长为0.4、0.04等，获得的最优阈值也可能是0.4、0.16等。而改进算法之后，步长作为随时间的改变量，在误差范围内可认为算法最终获得的最优阈值必然为0.143。

评价算法精度，最终是看小波包阈值降噪的效果。去噪方法的优劣都要用去噪的质量来评价，而信噪比(SNR)和均方根误差(RMSE)是被广泛采用的评价标准,信噪比越大且均方根误差越小，则去噪效果越好。

(19)

(20)

图9 不同阈值重构信号

列出各个重构信号与原始信号的信噪比和均方根误差，如表1所示。

表1 去噪效果对比

对比图1和图9，结合表1可以看出，在未改进算法前，获得的最优阈值可能是0.4、0.16等。由图9可以看出，阈值为0.4和0.16的重构信号虽然去除了噪声，但是由于阈值设置偏大，同样也去除了部分有用信号。而改进算法之后，获得的最优阈值为0.143，对应重构的信号，既去除了噪声又很好地保留了有用信号，虽然有局部噪声，但是在误差允许范围内可以忽略。且通过表1中的比较，阈值为0.143的重构信号效果好。

4 结论

结合粒子群动态优化算法，将阈值步长设为随时间变化的因变量，利用样本熵曲线来确定最优小波包阈值。以激光引信发射过载信号为例，对比分析了人为选择固定阈值步长而可能获得的最优阈值和算法选择的最优阈值的去噪效果。结合粒子群动态优化算法改进了样本熵寻找最优小波包阈值的缺陷，避免了陷入局部最优解以及人为选择步长误差的影响，获得的最佳阈值去噪效果更好。