基于电子鼻的气体识别神经网络算法研究
崔恩培,芶嵩淋,纪 越
(天津工业大学 电气工程与自动化学院,天津 300387)
1 研究背景
甲烷(天然气)、乙烷、丙烷、氨气和乙醇是我们生活中常常会接触到的几种气体,这些气体在达到一定浓度后均有一定的危险,存在安全隐患。而甲烷、乙烷、丙烷均为无色无味气体,难以察觉,且三者均为易燃气体,浓度高了容易发生火灾和爆炸。氨气本身就为有毒气体,有强烈的刺激味,能灼伤皮肤、眼睛、呼吸器官的黏膜,人如果吸入过多,则会引起肺肿胀,甚至死亡。而厕所、建筑工地用的混凝土添加剂中常常有氨气散发,如果某处通风不好导致气体大量聚集,极易发生危险情况。乙醇在生活中更常见,人们常不以为意,可是乙醇蒸汽和空气能形成爆炸性混合物,极易形成安全隐患。为了避免这些气体所带来的安全隐患,如何能快速且准确检测上述气体成为亟待解决的问题。
长期以来,为了避免上述气体带来的隐患,人们努力保持室内良好通风,暂时并无相关家用电子鼻检测产品出现。电子鼻只被用在工业生产、恶臭检测、食品检测等方面。电子鼻是由有选择性的化学传感器阵列和适当的识别方法组成的仪器,能够获取气体的数据信息,有效识别各类简单气体包括无色无味的人类难以察觉的气体。目前的气体传感器技术已经有足够精度来检测生活中这些有可能带来安全隐患的气体,且具有高灵敏度、可靠、可重复等特点,在生活用危险气体检测方面有很大潜力。
以前,对气体数据进行模式识别的方法主要靠支持向量机或BP 神经网络,可是近年来,随着深度学习的发展,许多改善神经网络的方法被提出并得到了广泛认可,在大数据样本的情况下BP 神经网络的表现已远超支持向量机。
目前,国内外已有学者将改进的BP 神经网络用于气体检测,胡晓楠、辜文祥先后研究了利用深度学习补偿电子鼻传感器漂移来提高识别率[1-2],但还没有针对上述生活中常见的且一定浓度后具有安全隐患的气体进行识别研究,因此在本文中,我们用电子鼻对甲烷、乙烷、丙烷、氨气和乙醇进行检测,并从激励函数和参数优化算法两个方面探讨不同的BP 神经网络对识别效果的影响。
2 样本、仪器和方法
在本实验中,我们自己选用了来自日本FIGARO 公司的6 款气体传感器及其信号调理和数据采集电路构成用于本实验的电子鼻系统。6 个气体传感器均为金属氧化物半导体型传感器,对气体敏感的部分由集成的加热器以及在氧化铝基板上的金属氧化物半导体构成。当空气中有被测气体存在时,该气体的浓度越高,传感器的电导率也就越高。我们进而将电信号转换为可解释的数据模型。不同传感器最为敏感的对象气体如表1 所示,TGS2603 的主要敏感气体是三甲胺和甲硫醇,其对氨气有较高的灵敏度。

表1 气体传感器阵列
2.1 气体样本
本实验所用气体样本采用大连大特气体公司生产的标准气体,包括氨气、甲烷、乙烷、丙烷和乙醇。实验所用气体及其浓度如表2 所示。
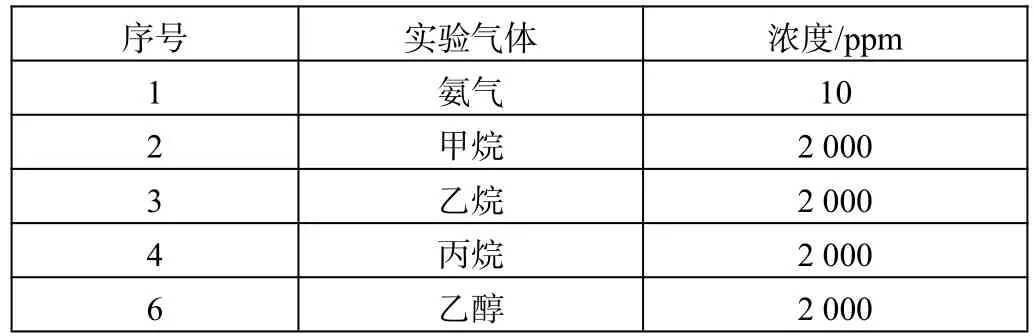
表2 实验所用气体浓度
2.2 数据采集方法
将电子鼻置于两侧有开口的气室内,从其中一侧匀速通入气体样本,气体从另一侧开口流出,同时电子鼻系统将采集到的数据发送至上位机,每0.5 s 采样一次,获取足够的气体数据。更换气体样本时先通入600 s 的空气,确保上次实验气体完全排除后再通入新被测气体的样本。最后将得到的数据进行标注和清洗,实际得到有效数据10 950 组,随机取7 950 组为训练数据,3 000 组为测试数据,处理完成后利用神经网络算法进行识别训练和测试。
2.3 气体识别方法
神经网络是一种由大量的节点(或称“神经元”)和之间相互联接构成的运算模型。每个节点代表一种特定的非线性输出函数,称为激励函数。神经网络的训练情况通过定义好的损失函数来进行评估,BP 算法则是对网络预测值和期望值的差值进行反向传播优化网络权重参数的算法,尽量让网络的损失函数输出值达到最小。
本文采用Xavier 方法[3]初始化神经网络参数,利用拥有2 个隐含层的深层BP 神经网络对危险气体进行识别。在第一隐含层25 个神经元,第二隐含层12 个神经元,整个训练集分为50 个Minibatch 的情况下训练1 000 代,即遍历1 000次训练集进行训练,同时设学习速率为0.000 2,用Softmax loss 函数作为损失函数评估神经网络。
在传统的神经网络中,常用Sigmoid 函数作为神经网络的激励函数,并利用梯度下降法来优化神经网络。然而随着Jarrett 等人[4]利用ReLU 作激活函数使用,Kingma D 等人[5]利用Adam 算法来优化神经网络,ReLU 函数和Adam 的优势显现出来。本文采用ReLU函数作为神经网络的激励函数,且采用Adam 算法来优化神经网络。
2.3.1 激励函数
激励函数让神经网络的输出变为非线性函数。传统的Sigmoid 函数是将输入值归一化到(0,1)之间。Sigmoid函数图像如图1 所示。Sigmoid 函数公式为:


图1 Sigmoid 函数图形
在Sigmoid 函数中,如果输入值较大或较小,输出的值会非常接近于1 或0,也就是在Sigmoid 函数的输入较大或较小时,它的输出变化会非常小,导致这部分函数的导数非常接近于0,而人工神经网络在反向传播时,损失是以导数的形式不断向上一层传递以调整权重优化参数。所以如果导数无限接近于0,参数优化就会非常慢,发生梯度消失现象。ReLU 函数在输入小于0 时输出值恒为0,在输入大于0 时,输出线性增长。ReLU 函数图像如图2 所示。ReLU 函数公式为:

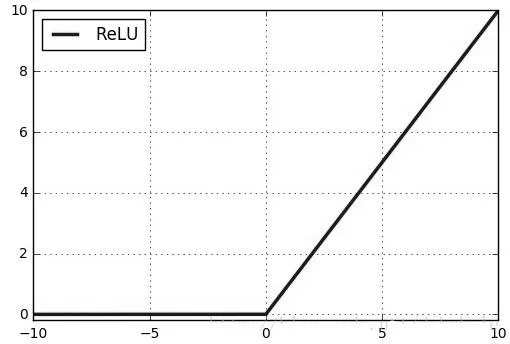
图2 ReLU 函数图形
ReLU 函数在其输入小于0 时输出为0,大于0 时输出成线性增长。所以理论上ReLU 函数不会在反向传播时出现梯度消失的情况,学习效果会更好。同时ReLU 函数计算简单,未涉及指数运算,在一定程度上能缩短网络的训练时间。
2.3.2 优化算法
优化算法的功能是通过改善训练方式,最小化损失函数。梯度下降法是为了找到网络中最优的权重参数,使网络损失最小。就是通过对函数求导得到梯度方向,然后沿梯度下降的方向按一定的步长求解极小值的过程。梯度下降法公式为:

式(3)中:η为学习率(步长)。
在梯度下降法中,权重更新的快慢是由学习率η决定的,学习率是一个固定的值,如果学习率太小则训练太慢,如果学习率太大则不容易收敛到最优值。在训练神经网络时,人们更希望对经常出现的数据使用小的学习率,而对罕见的数据使用较大的学习率。
Adam 算法根据损失函数对每个参数的梯度的一阶矩估计和二阶矩估计动态调整针对于每个参数的学习速率。Adam 算法也是基于梯度下降的方法,但是每次迭代参数的学习步长都有一个确定的范围,不会因为很大的梯度导致很大的学习步长,参数的值比较稳定。Adam 算法的过程如下:

Adam 算法在优化过程中利用衰减系数β1计算了梯度的平均值,又利用β2计算了梯度平方的均值,在此基础上实现学习率的动态调节,理论上可以达到不同参数具有不同学习率的目的,提高网络的准确率和训练速度。
在本实验中设β1为0.9,设β2为0.999,设ε为10-8.
3 实验结果与分析
电子鼻对不同气体的响应变化如图3 所示。


图3 不同气体的响应曲线
从图3 中可以看出,不同传感器对不同气体的响应均有差别。图3(b)TGS2611 的数值从1 800 升至2 500.图3(e)中,TGS2620 的数值明显升高至接近3 000.在上述实验方法和条件下,将两种激励函数和两种优化算法两两组合,通过损失函数梯度下降的情况和它们分别在训练集和测试集上的成功率来判断人工神经网络的训练情况。不同模型的梯度下降过程如图4 所示。不同模型在训练数据和测试数据上的识别准确率如表3 所示。

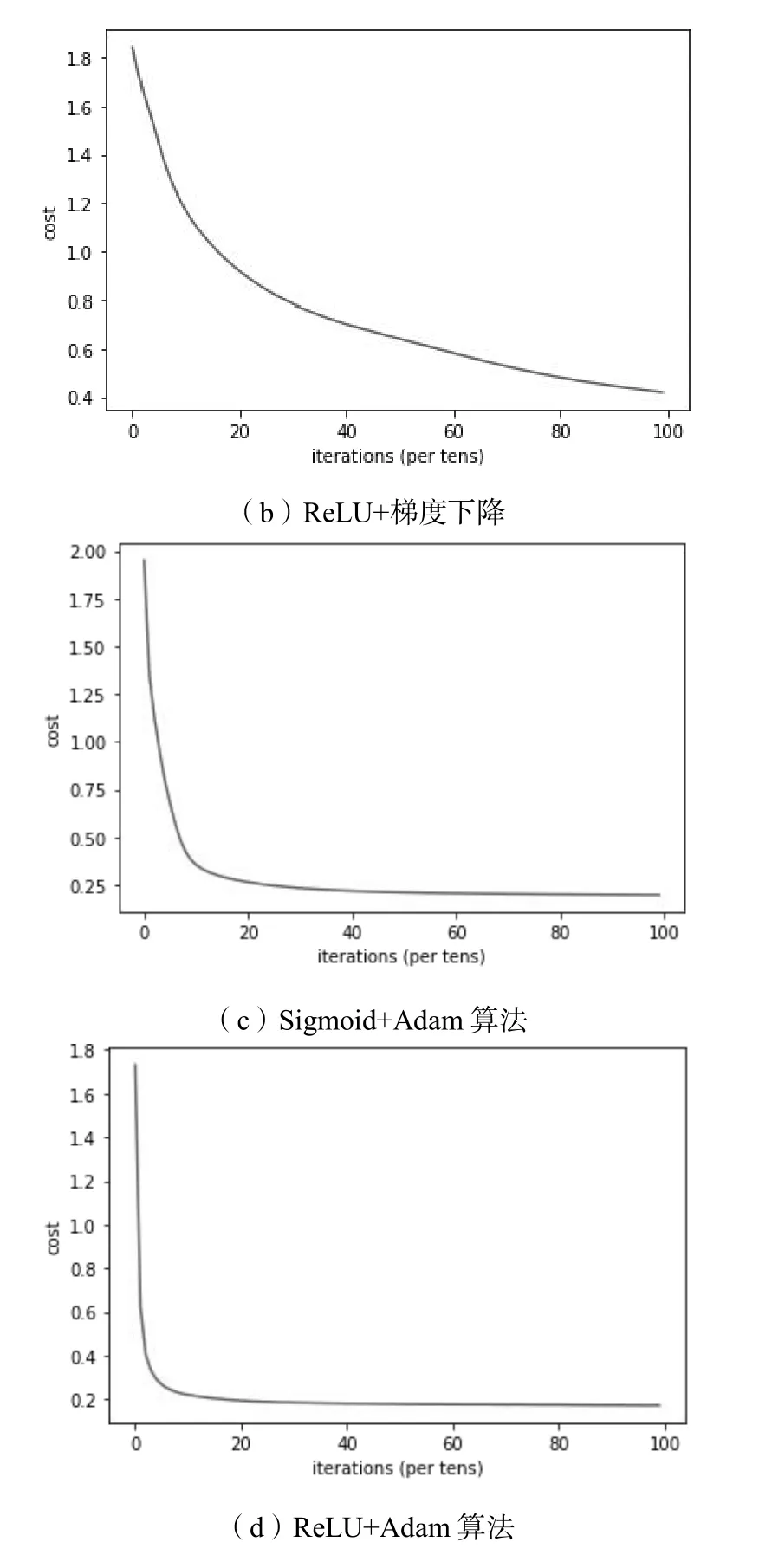
图4 不同模型的梯度下降过程(Learning rate=0.000 2)

表3 不同模型在训练集和测试集上的准确率
如图4(a),在1 000 代的迭代后,使用sigmoid 函数和梯度下降法训练的网络损失仅下降到1.3 左右,且仍有明显的下降趋势,说明该网络并未训练完成,需要更多的迭代次数。仔细观察发现,在50~400 代左右的迭代范围内损失下降速度非常慢,出现了梯度消失现象。检查该网络在训练集和测试集上的识别准确率,仅为44.6%和44.2%,此时的气体识别效果并不理想,如果想要使成功率提升,让损失进一步下降,则需要进行更多的迭代来训练网络。
如图4(b),在1 000 代的迭代之后,使用ReLU 函数和梯度下降的网络损失下降到0.4 左右,且下降速度已经开始减慢,说明此时已经接近损失的最小值,网络已经训练到不错的水平。检查该网络在训练集和测试集上的识别准确率,分别达到了88.8%和88.7%,识别效果较为良好。但此时距离最优仍有一小段距离,仍可继续训练以减小损失。
如图4(c),使用Sigmoid 函数和Adam 算法的网络在迭代到200 代的时候损失值接近0.25,网络的训练速度较快,比起使用梯度下降的网络有了大幅提升,之后仍有下降但非常小,说明该网络几乎找到了最优解。该网络在训练集和测试集上的识别准确率分别达到了92.7%和91.8%,已经提取到了可靠的气体数据特征并做出了较好的识别。
如图4(d),使用ReLU 函数和Adam 算法的网络在几十代的迭代过程中损失迅速下降至0.2 左右,表明在这种情况下的网络训练速度非常快。之后的训练中将损失稳定降到了0.2 以下且一直稳定几乎不变,可以认为此时该网络已经找到了损失函数的最小值。该网络在训练集和测试集上的识别准确率分别达到了93.3%和92.1%,说明该网络已经很好提取到了气体数据的基本特征。
综上所述,利用ReLU 函数作为激励函数的网络不论在识别准确率还是在训练速度上,都远远优于同等条件下使用Sigmoid 作激励函数的网络,在使用梯度下降法优化网络的情况下,使用ReLU 网络的识别准确率比使用Sigmoid 网络的高44.2%;在使用Adam 算法优化的情况下,前者也要比后者高出0.6%,同时使用ReLU 的网络训练速度也有不同程度提升。
此外,在使用Sigmoid 作为激励函数的情况下,利用Adam 算法优化的网络在识别准确率上比使用梯度下降法的网络高48.1%;在使用ReLU 作为激励函数的情况下,前者相比于后者准确率提升了4.5%,使用Adam 算法优化的网络训练速度也显著快于使用梯度下降的网络。实验证明ReLU 和Adam 算法均能提升用于气体检查识别的神经网络的效率,与理论吻合。
4 结论和推广
在利用电子鼻和人工神经网络对气体的检测和识别中,利用ReLU 函数作为网络的激励函数和使用Adam 算法优化神经网络能大幅提高传统神经网络的效率,且效果显著。在同时使用两种方法的情况下,准确率能达到93.3%,对上述5 种气体能起到良好的识别效果。本文验证了ReLU 函数和Adam 优化算法在对气体识别神经网络上的优势,为今后在气体检测的神经网络识别算法方面提供了优化思路。

