多汇聚节点无线传感网络充电路径多目标优化方法*

夏静山,庄哲民*,Alex Noel Josephraj,郑大为

(1.汕头大学电子工程系,广东 汕头 515063;2.伊顿电气集团山特电子(深圳)有限公司,广东 深圳 518101)

节点能量消耗管理问题,一直是无线传感网络WSN(Wireless Sensor Networks)领域的研究热点[1-2]。降低节点能耗,延长网络生存周期的方法有多种,如采用低能耗路由协议[3]、优化网络覆盖算法[4]、提高电池容量等。在多汇聚节点WSN[5]中,由于汇聚节点能量消耗速度快且需要长时间持续稳定工作,以上方法均不能保证节点有持续的能量供应,尤其在环境恶劣的重要区域,比如地下煤矿、隧道、野生动物保护地等,网络需要工作数年之久,汇聚节点需要时刻处理大量且复杂的数据并上传,节点电池又无法人工更换,一旦某个汇聚节点能量消耗殆尽,网络寿命也会随之结束。鉴于无线能量传输技术[6]已较为成熟,因此可以通过无线充电为汇聚节点补充能量,延长网络寿命。当网络中汇聚节点数量过多或者分布过于离散时,可对整个网络区域进行网格划分,得到多个子区域,然后分区域进行能量补充。在每次能量补充前,需要先对充电路径进行规划:在充电过程中,不仅要保证每个汇聚节点都能够正常工作,还要使充电路径总距离最短、充电消耗总能量最少,而且距离和能量不是相互独立的,这是一个多目标旅行商问题MOTSP(Multi-Objective Traveling Salesman Problems)。

目前,对MOTSP的算法研究已较为成熟,如遗传算法[7]、蚁群优化算法[8]、模拟退火算法[9]等。Davoodi[10]提出一种求解网格中双目标和寻找Pareto前沿的确定性算法,该算法得到的最优解精度较高,但时间复杂度过高,即时性低;汪勇等[11]以模式理论为基础,提出一种基因重组法,并采用熵值法确定路程和费用权重,算法计算效率较高,但该算法对于有时变约束条件的问题较为吃力;文献[12-13]分别采用混合遗传算法和改进分组遗传算法来求解MOTSP,二者收敛速度较快,但计算效率偏低;Cornu等[14]提出一种基于多目标集合的摄动分解算法(PDA)来解决MOTSP,PDA结合了分解方法、局部搜索和数据扰动的思想,为寻找帕累托锋的近似解提供了两阶段模块化框架,该算法应用广泛,可计算四目标及以上的MOTSP,鲁棒性好,但是对于非对称TSP适用性较低;Xia等[15]将共生有机体搜索算法与模拟退火算法相结合,来解决大型TSP,结合后的算法求解效果很好,但运算复杂度高,即时性偏低。

本文待充电节点的剩余能量是时变减少的,属于非对称链路,且即时性要求高,为了保证其在任意时刻均不低于节点正常工作所需最低能量,本文提出了一种基于能量约束条件的改进多目标优化遗传算法。通过目标转化和加权,建立多目标优化问题模型,并对遗传算法的选择、交叉、变异算子作出改进。通过仿真证明了该算法可以有效的延长多汇聚节点WSN的寿命。

1 基本问题描述

本文将多汇聚节点无线传感网络充电路径优化问题描述为:在一个多汇聚节点无线传感网络中,维护基站P作为无线充电小车WCC(Wireless Charging Car)行驶路径的起点和终点,即在某一时刻基站检测到网络中有n个汇聚节点处于设定充电阈值范围内,需要补充能量,WCC便从P出发,依次对这些节点进行充电,充电任务完成后返回维护基站P。

我们的求解目标是:找到一条充电路径,不仅可以使剩余能量越少、能量消耗速度越快的的汇聚节点优先充电,从而保证每个汇聚节点都能够正常工作,而且充电路径总距离最短、消耗WCC的能量最少。由于最低剩余能量约束只限定于汇聚节点,因此路径规划中不考虑以P为起点和终点的路段,即以第1个充电节点为路径起点,最后一个充电节点为路径终点。我们假定在遍历的充电路径中,对需要充电的节点,只充电一次。

2 多目标路径优化算法设计

2.1 多目标优化数学模型

为了解决该多目标路径优化问题,我们将节点优先充电的目标转化为能量约束条件ECC(Energy Constraint Conditions),并建立路径总距离S和消耗WCC总能量E的数学模型。假设各汇聚节点之间完全连通,用Wk={Wk(1),Wk(2),Wk(i),…,Wk(n)}表示第k条充电路径,k=1,2,…,n!。Wk为节点1～n的任意一个路径排列组合,Wk(i)表示该充电路径上的第i个节点,Wk(1)即为充电起始节点。建立模型如下。

①距离目标

设节点Wk(i)的位置坐标为(xi,yi),则WCC从节点Wk(i)行驶到节点Wk(i+1)所前进的距离d[Wk(i),Wk(i+1)]可表示为:

(1)

将任意路径Wk所对应的路径总距离S(Wk)作为距离目标函数:

(2)

②能量目标

首先作出以下假设:充电过程开始时,汇聚节点Wk(i)的初始剩余能量为EIR[Wk(i)];WCC每次充电时,都把该节点能量充至电池容量Emax[Wk(i)];充电过程结束后,网络中所有汇聚节点均不需要充电。

消耗WCC的能量分为两部分:一部分是WCC在行驶过程中消耗的能量E1(Wk),

(3)

式中:V为WCC行驶速度,RM为WCC行驶时自身能量消耗速度,二者均为常量;

另一部分是为节点充电而消耗的能量E2(Wk),可通过充电消耗总时间乘以充电速度求得,表达式如下:

(4)

式中:Emax[Wk(i)],RC,R[Wk(i)]分别为电池容量、充电速度、节点平均能量消耗速度,均为已知参数。节点在进行能量补充时,仍然在正常工作,因此在分母中充电速度需要减去节点能量消耗速度。ER[Wk(i)]为待求量,表示WCC刚到达节点Wk(i)时,该节点的剩余能量,可由下式求出:

ER[Wk(i)]=EIR[Wk(i)]-TA[Wk(i)]×R[Wk(i)]
1≤i≤n

(5)

式中:EIR[Wk(i)]为已知的初始剩余能量,TA[Wk(i)]为从充电过程刚开始至WCC刚到达节点Wk(i)消耗的时间,易知TA[Wk(1)]=0。当i>1时,TA[Wk(i)]表达式如下:

TA[Wk(i)]=TA[Wk(i-1)]+TM[Wk(i)]+
TC[Wk(i-1)],2≤i≤n

(6)

式中:TM[Wk(i)]为WCC从节点Wk(i)的前一个节点移动到该节点的行驶时间,TC[Wk(i)]为WCC对节点Wk(i)的充电时间。式中存在递归关系,通过求出前一个节点的到达时间和充电时间以及从前一个节点到当前节点的行驶时间,三者求和,便可求出当前节点的到达时间。令TM[Wk(1)]=0,当i>1时,TM[Wk(i)]表达式如下:

(7)

WCC对节点Wk(i)的充电时间TC[Wk(i)],通过充电所补充能量除以真实充电速度来计算,表达式如下:

(8)

联合式(5)～式(8),通过不断递归,便可分别求出式(5)～式(8)中的各个待求量,包括ER[Wk(i)],进而求出式(4)中的E2(Wk),则Wk对应的能量目标函数E(Wk)可表示为

minE(Wk)=E1(Wk)+E2(Wk)

(9)

③等价目标转化和加权处理

由式(3)可知,E1(Wk)与S(Wk)成正比,因此我们将原双目标等价转化为S(Wk)和E2(Wk)的双目标优化。由于在算法中同时设计两个目标函数会大大增加算法的复杂度,而且难以得出使两个目标都同时达到较优的结果,因此我们再次对S(Wk)和E2(Wk)进行等价转化,将S(Wk)转化为t1(Wk),即WCC到达所有需充电的节点的行驶时间之和:

(10)

将E2(Wk)转化为t2(Wk),即所有节点的充电时间之和:

(11)

式(10)、式(11)可分别通过式(7)、式(8)求解,由于V、RC均为常量,所以该转化是等价转化。

然后对目标t1(Wk)和t2(Wk)进行加权,设权重分别为α和β,则由式(10)和(11)线性加权得到多目标优化模型的目标函数为

(12)

式中:α和β满足α+β=1。取α=β=0.5,并将t(Wk)放大两倍,即把整个充电过程消耗的总时间TSUM(Wk)作为本文的多目标优化模型的目标函数:

(13)

式中的两个待求量在前文已通过式(7)、式(8)求出。目标函数确定后,还需要确定能量约束条件ECC,ECC包括:节点初始剩余能量EIR要低于设定充电阈值Eth;ER在任意时刻都要高于节点正常工作所需最低剩余能量Emin,即节点在任意时刻均可正常工作;消耗总能量E(Wk)要小于WCC携带总能量EC。ECC表示如下:

(14)

式中:ER[Wk(i)]为WCC刚到达节点Wk(i)时,该节点的剩余能量,Emin[Wk(i)]为节点Wk(i)正常工作所需最低能量。

2.2 改进的多目标路径优化遗传算法

针对前面提出的多目标优化模型,本文采用改进的遗传算法(Improved Genetic Algorithm,IMGA)来求解。其中式(13)中的TSUM为改进遗传算法的目标函数f,当ECC不成立时,设定f为一个较大的常数C,经过多次仿真测试,最终取C=27.5。由于本文优化问题是求取最小值,因此适应度函数与目标函数为负相关关系,适应度函数F为:

(15)

式中:A为放大系数,经过多次仿真测试,取A=50。另外,本文编码方式为顺序编码;为了提高种群的状态遍历性,采用随机方式生成初始种群,种群规模为popsize,种群规模不宜太小也不宜太大,取popsize=120,路径Wk即为种群中的一个个体;采用最大迭代次数GN作为遗传算法的终止条件,GN太大会降低算法的即时性,太小会降低算法的性能,取GN=300。

算法具体改进如下。

为了避免种群最优适应度在迭代过程中出现下降的情况,本文采用与最佳个体保存策略相结合的轮盘赌法进行选择操作。另外,为了提高适应度高的个体的选择概率和算法运行效率,我们对适应度函数作一个乘方变换。对于个体Wk,设其适应度为Fk,则该个体被选中的概率Pk为:

(16)

式中:q为乘方变换阶数,q过小会导致不同个体被选择的概率相差较小,过大会增加算法的计算量,本文取q=15。

为了避免交叉操作产生非法路径,并提高种群多样性,本文采用交叉点不固定的部分匹配交叉算子(PMX)[16]、随种群进化阶段而变化的交叉概率,并加入亲子竞争机制,进行交叉操作。为了提高种群进化效果和后期种群稳定性,交叉概率应随种群进化阶段(分为前期、中期、后期)逐步变小,分段交叉概率如下式所示:

(17)

式中gn为算法当前迭代次数,GN为算法最大迭代次数,3个分段分别对应种群进化的前期、中期、后期。

为了提高算法的全局搜索能力,本文采用变异点不固定的逆序变异和互换变异相结合的复合变异方式,并加入亲子竞争机制,进行变异操作。变异概率是一个较小的数,依据种群进化阶段设定如下:

(18)

式中gn为算法当前迭代次数,GN为算法最大迭代次数。

2.3 算法流程图

IMGA的算法流程图如图1所示。从图1中可以看出,改进后的遗传算法相比于简单遗传算法并没有增加循环嵌套部分,而是采用了更优的遗传算子,因此时间复杂度没有变化,仍为o(n);由于采用了较复杂的遗传算子,因此计算复杂度相比于简单遗传算法有增加,但是大大提高了算法的寻优能力和全局搜索能力。

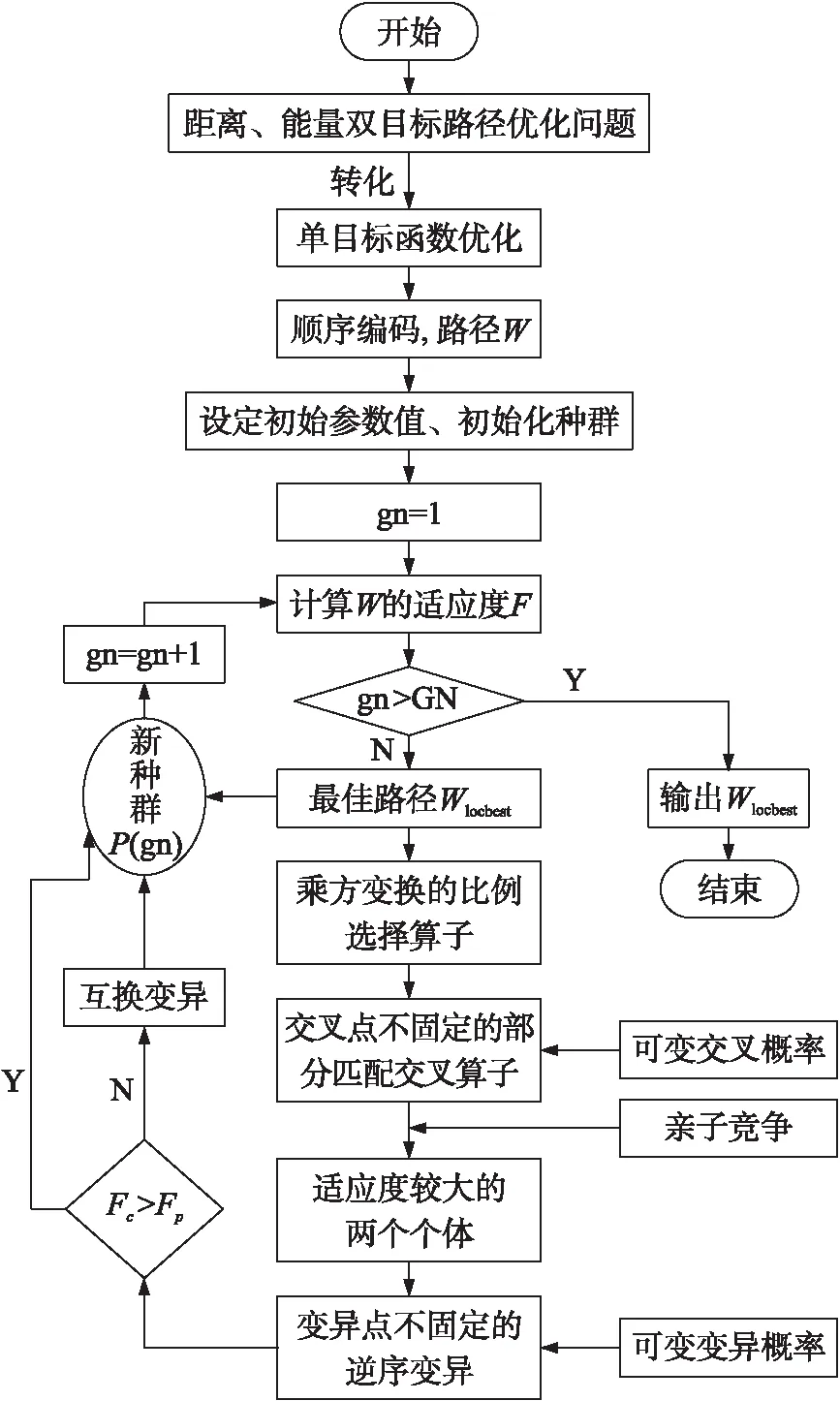
图1 IMGA算法流程图

3 仿真实验

3.1 仿真平台

本文仿真环境为MATLAB R2014a,采用MATLAB语言与C语言混合编程,其中程序主体用MATLAB编写,一些耗时的函数用C实现,对改进的遗传算法和简单遗传算法进行分析比较,得到多目标优化问题的最优解。

3.2 仿真参数

在800 m×400 m区域内,随机部署一定数量的汇聚节点和大量的普通传感节点,基站P位置坐标为(400,200)。假设某一刻处于充电范围内的汇聚节点数量为10个。为了使模拟仿真更接近实际情况,提高实验结果的代表性,在选取这10个节点时,节点位置随机,初始能量异构,能量消耗速度也各不相同;为了避免电池深度放电,延长电池使用寿命,我们设定Emin=0.05Emax,Eth=0.2Emax[6]。节点的能量参数和位置参数分别如表1和图2所示(这里能量单位为库伦,C)。

表1 节点能量参数

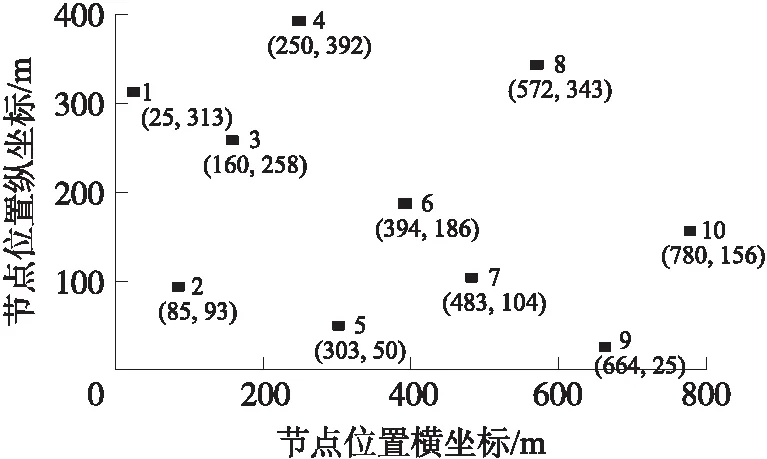
图2 待充电汇聚节点位置

图2中,黑色点即为待充电汇聚节点,右边的数字为节点编号, 下方的数字即为节点位置坐标。考虑实际情况,节点部署环境较为恶劣,无线充电小车WCC相关参数设定如下:EC=26 000 c;V=280 m/h;RM=18 c/h;RC=1 800 c/h。

3.3 仿真结果与分析

3.3.1 最佳充电路径及算法有效性验证

运行IMGA可以得到最优充电路径Wbest={2,9,8,10,7,6,5,3,1,4},为了验证该路径满足能量约束条件,可以保证节点持续正常工作,我们选取充电过程的4个状态(WCC刚到达起始节点、节点10、节点5、终点节点),来展示未充电节点的剩余能量ER的变化过程。具体展示如图3所示。

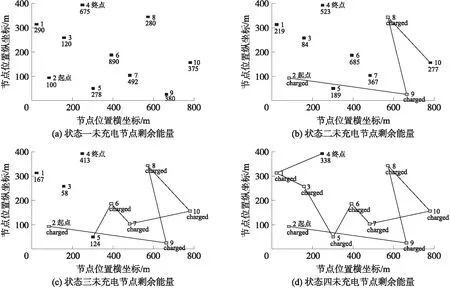
图3 最优路径分状态展示图

图3中,黑、白色节点分别表示未充电节点、已充电节点,黑色节点下方的数字即为当前状态下该节点的剩余能量ER。综合比较4个状态可以看出,未充电节点剩余能量在不断减少,但始终没有低于表1中设定的最低值Emin。另外,由式(9)可以求出该路径消耗WCC总能量为23 991.36 c,小于WCC携带总能量EC。因此该路径能够满足能量约束条件,可以有效的延长网络寿命。

3.3.2 IMGA与SIGA性能对比

我们从最优解精度、种群收敛速度、种群进化效果3个方面来评价 IMGA和SIGA的性能。IMGA和SIGA运行结果如图4所示。

图4 两算法运行结果

图4(a)中,实线代表IMGA运行得到的最优路径;虚线代表SIGA运行得到的最优路径。

①最优解精度POS

将IMGA运行200次,得到200条最优路径,我们取其中对应目标函数f值最小的路径作为本文多目标优化问题的理论最优路径WTH,WTH= {2,9,8,10,7,5,6,4,3,1}。由式(13)可得f(WTH)=21.83 h,IMGA、SIGA得到的f(Wbest)分别为21.87 h、22.07 h,则IMGA、SIGA的最优解精度分别为99.82%、98.90%,优化率0.92%。

②种群收敛速度SPC

算法取得最优解的代数越早,种群收敛速度就越快。从图4(b)可以看出,IMGA、SIGA约分别在第14、101代取得最优解,因此IMGA种群收敛速度要优于SIGA,优化率为86.14%。

③种群进化效果EPE

在算法迭代过程中,如果种群平均解逐渐逼近种群最优解,则算法的种群进化效果较好。从图4(b)可以明显看出,IMGA的种群进化效果要优于SIGA,计算得二者EPE分别为99.41%、95.15%,优化率4.26%。

对比结果如表2所示。

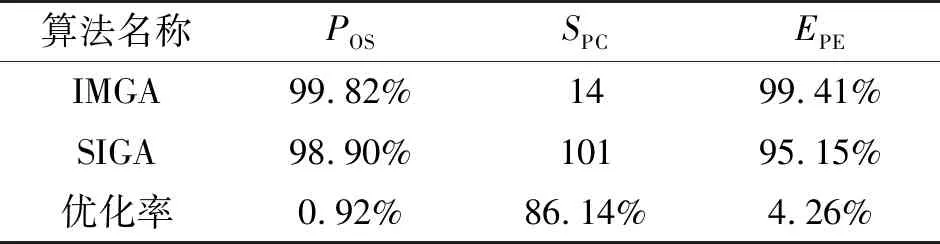
表2 算法性能对比

3.3.3 与单独考虑距离、单独考虑能量两种方法结果比较

由于本文对距离和能量多目标优化进行了量纲转化和加权处理,因此为了验证本文方法的优越性,我们将本文方法与单独考虑距离和单独考虑能量两种方法进行比较。在分别得到最优路径Wbest后,根据式(2)、式(5)、式(9)、式(13)可分别求出S、ER、E、TSUM。3种方法结果对比如表3所示。

表3 3种方法结果对比

从表3中可以看出,单独考虑距离方法得到的最优路径对应的S比本文方法小很多,但是节点9和8能量已消耗殆尽,达不到我们延长网络寿命的目的;单独考虑能量方法得到的最优路径对应的E比本文的方法要少0.039%,但是S却比本文方法多10.78%,导致TSUM比本文方法多了将近1 h,得不偿失。因此,本文采取的方法是要优于其他两个方法的。

4 结束语

多汇聚节点无线传感网络中的汇聚节点需要长时间持续工作,但节点能量有限,因此需要通过持续的能量补充延长网络寿命。本文采用移动充电小车来对节点进行充电,并设计了一种多目标充电路径优化方法,通过改进的遗传算法对充电路径进行最优规划,得到一条最佳充电路径。通过实验也表明了,该方法可以有效地延长整个网络的生存周期,而且可以较好的降低能量补充成本。