基于KPCA和改进GBRT的室内定位算法*
李新春,房梽斅,张春华
(1.辽宁工程技术大学电子与信息工程学院,辽宁 葫芦岛 125105;2.辽宁工程技术大学研究生学院,辽宁 葫芦岛 125105; 3.中国联合网络通信集团有限公司阜新市分公司,辽宁 阜新 123100)
目前,随着互联网和移动终端的全面普及,基于位置服务的相关技术在民用、商用、军用等定位场所的应用越来越广泛[1-2]。在室外环境中,GPS可实现高精度定位,但在室内环境中,由于接收信号强度受到室内建筑物结构布局以及人员遮挡等因素限制[3],基于无线局域网络WLAN(Wireless Local Area Networks)的位置指纹定位算法更有优势[1,4]。目前WLAN网络的覆盖率越来越高,基于WLAN定位具有成本低、设备功耗小、布网方便等优点,使其成为获取接入点数量AP(Access point)无线信号强度的首选[5]。在传感器和移动网络环境中,无线网络更容易受到干扰,协作传输过程,外来接入点有机会充当中继,接收信号强度RSS(Received Signal Strength)值的波动性更大[6],有必要快速准确地提取其主成分。
通常情况下,指纹定位算法主要分为两个阶段[7]:离线训练阶段和在线定位阶段。离线训练阶段采集参考点来自各个AP的RSS值,构成原始位置指纹向量X,与其物理位置Y一一对应,构成离线数据矩阵(X,Y),通过训练得到RSS值和其位置坐标的映射关系Y=f(X),构成指纹库;在线阶段采集待测参考点的信号强度,构成在线位置指纹向量X*,利用离线阶段构成的匹配回归模型,预测待测参考点的位置坐标Y*。这种室内定位模型的定位精度主要取决于离线阶段和在线阶段是否服从同一定位模型。
室内定位算法有KNN、WKNN和PCA-WKNN 3种传统算法。KNN是一种监督式机器学习算法,在线阶段对待测点RSS值分别计算它与指纹库中各个向量的欧式距离,选取最近的多个指纹作为预测位置;WKNN算法对指纹库中各个向量给予权重,权重与欧式距离成反比,使其结果更接近真实性;PCA-WKNN算法采用PCA算法对离线获取的RSS矩阵降维,在线阶段利用WKNN算法进行对比。针对以上传统算法,许多专家学者进行了改进。
文献[8]采用PCA算法对RSS矩阵进行降维,提取其主要特征信息,通过RSS的特征与其对应位置关系,对测试点的位置进行预测;文献[9]利用PCA方法降维处理离线阶段获取的位置指纹,以解决因外在环境问题对信号强度获取造成的不确定测量,采用LSSVR算法通过非线性映射使低维不可分样本映射到高维空间,使位置指纹做线性可分类处理。文献[10]采用单乘法神经元(SMN)算法来提高定位精度,离线和在线阶段均采用PCA算法来减小RSS的维度并消除噪声。以上3种算法直接进行降维处理,均未充分利用位置指纹之间的特征信息,导致训练的离线回归模型不能准确定位待测点,定位误差较大。文献[11]采用支持向量机(SVM)对离线阶段各接入点的信号强度信息进行特征提取,并用WKNN算法进一步分类,创建离线指纹数据库,在线阶段利用指纹库特征值去修正定位误差;文献[12]采用分段匹配追踪算法来构造离线指纹数据库,在线阶段采用最小二乘算法预测位置信息;文献[13]采用非线性偏最小二乘法(PLS)减少指纹数据库维度,并采用内部相关向量机(RVM)训练离线回归模型。以上3种算法未根据特征信息的优劣训练离线回归模型,导致定位误差较大,且在线阶段不能快速实现定位,虽在一定程度上提高了定位准确度,但在训练离线指纹数据库方面仍需改进。
本文针对上述室内定位算法定位准确率不高的问题,提出了一种基于KPCA和改进GBRT的室内定位算法。在离线阶段,采用KPCA算法提取RSS主成分,并利用改进GBRT算法训练离线回归模型;在线阶段根据离线回归模型预测位置信息。通过仿真实验结果表明,在相同定位条件下,本文室内定位算法在AP数量、RSS样本数量等方面均优于传统的PCA-WKNN室内定位算法、文献[10]的SMN-PCA算法和文献[13]的RVM-PLS算法,定位误差更小,实际应用效果更好。
1 基于KPCA和改进GBRT的室内定位算法
基于KPCA和改进GBRT的室内定位算法,命名为KPCA-IGBRT,定位算法流程如图1所示。
1.1 原始指纹向量采集及预处理


图1 KPCA-IGBRT室内定位算法流程
由于RSS值的不稳定性,同一位置接收的RSS值波动较大,在定位算法处理之前,首先需要对RSS值进行去噪处理。
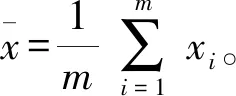
(1)
利用贝塞尔公式计算数据的标准差s,如式(2)所示。
(2)
计算格拉布斯检验统计量Gi,如式(3)所示,其中i为异常值的排列序号。
(3)
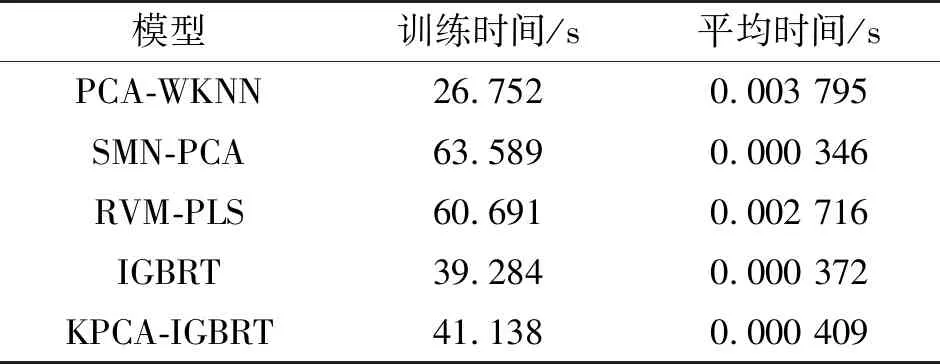
依据格拉布斯(Grubbs)法,把Gi与格拉布斯表[14]给出的临界值Gp(n)相比较,若Gi 采用式(4)标准化RSS值,使每一个RSS值都在0~1范围内,用来简化和加速训练过程。 (4) 主成分分析(PCA)方法是识别领域中的经典算法,主要利用降维的思想,把高维中的有效特征信息在低维空间中明显地展示出来;而KPCA算法[15],主要方式是采用核函数,将原始指纹矩阵在低维空间不能明显显示的特征信息,通过非线性映射函数Φ在更高维的特征空间Q上表现出来,并对Q降维运算,其中心思想是尽可能多地保留训练集中方差的同时,减少该特征训练集的维度[16]。 设非线性映射函数Φ将原始位置指纹空间F={F1,F2,…,FM}映射到更高维度的特征空间Q={Φ(F1),Φ(F2),…,Φ(FN)},由于特征空间Q非中心化,需对其做中心化处理,如式(5)所示。 (5) 求解中心化的特征空间Q′的协方差矩阵,如式(6)所示。 (6) 计算协方差矩阵特征值λ及其对应的特征向量V,如式(7)所示。 (7) (8) (9) 定义N×N阶核函数K,它的各个元素表达式如式(10)所示。 Kij=(Φ(Fi)TΦ(Fj)) (10) 进一步推导则有 (11) 进一步化简可得 (12) 其中矩阵C为N维矩阵,每个元素都是1/N,则式(9)可以化简为 (13) (14) (15) 将式(11)代入式(15)中可得式(16),即KPCA算法提取原始位置指纹的核主成分。 (16) 非线性映射函数Φ中,高斯核函数是最高效的,利用高斯核函数提取的核主成分可最大程度地表示数据间的非线性特征信息,高斯核函数如式(17)所示。 (17) 梯度提升回归GBRT算法是泛化能力较强的一种回归算法,由多棵决策树组成。而IGBRT算法主要采用自助抽样法,从初始训练集中有放回的均匀抽样构成多个子训练集。计算一个训练集的回归模型,初始时,GBRT算法为每一个低维空间的特征赋同一个初值,即每一个特征信息都一样重要。训练特征信息后每一次得到新的模型,会导致对特征信息的预测有一定的误差[17-18]。为了消除每一次训练特征信息的错误,通过在减小误差最快的方向上构建新的回归模型,且只需学习上一次模型的残差,使原来的模型的残差向梯度减小的方向上进行收敛。 IGBRT算法采用多个回归模型替代一个回归模型,从初始特征样本集中抽样,有放回地随机选取大小和特征集T一样的子特征集T(i),构成k个子特征集,作为各个回归模型的初始特征集。在一个子特征集中,可能含有多个重复的样本。 假设一个回归模型初始值如式(18)所示。 (18) 在构建一个回归模型过程中,首先找到最优切分点j与切分点s,如式(19)所示,递归地将每个区域划分为两个子区域,并计算每个子区域的输出值,构建一棵二叉决策树。 (19) 输入空间根据选定的(j,s)划分区域R决定相应的输出值,如式(20)所示。 Ti(RSS)=cmI (20) 回归模型继续学习真实值L与二叉决策树迭代后的预测值fk(RSS)的差,即拟合残差rki作为下一次学习的位置信息,如式(21)所示。 (21) 调用式(19)~式(21)循环迭代M次,结束生成M棵树。 将一个子特征集T(i)划分为M个区域R1,R2,…,Rm,得到m个二叉分类决策树,训练一个回归模型,如式(22)所示。 (22) 综上所述,IGBRT算法得到的强回归模型(23)由多个式(22)的回归模型组成。 (23) 在线定位阶段,测试点采集来自每个接入点的无线信号强度,构成在线位置指纹向量F,利用式(16)对F进行KPCA变换,得到位置指纹非线性特征向量F′,然后送入强学习模型式(23)进行学习,得到每个模型输出的位置信息,最终预测结果根据各个回归模型的预测位置输出的众数而定。 图2 实验定位区域 为验证本文改进室内定位算法的定位情况,考虑诸多因素后,实验场所选在辽宁工程技术大学静远楼进行,选择西门8 m×8 m的大厅作为实验场所,其定位区域如图2所示。在选定的定位场所中,包含立柱、装饰品等,并放置两排桌椅作为障碍物,在第1排桌子上放置手机、电脑等一些干扰装置。整个实验场所干扰噪声较复杂,采集的无线信号强度较不稳定但具有代表性。 采集数据过程起点为矩形中心,其初始的位置坐标设为(0,0)。数据采集位置如图3所示,参考位置以中心点为圆心,半径为1时,每隔60°选取参考点;半径为2时,每隔30°选取参考点;半径为3时,每隔20°选取参考点;半径为4时,每隔20°选取参考点。实验区域一共54个参考位置,其采集位置如图3中的RP;另外在定位场所选取10个测量点,采集位置如图3中的TP,可得到RP和TP真实的物理坐标;在线定位过程,测量待测点实时的无线信号强度,按照一定的顺序组成指纹向量,通过本文改进的回归模型估算待测点的物理坐标,并用估计坐标与实际坐标的比较结果,判断本文改进算法的定位情况。 实验过程中,在定位区域共布设8个AP设备,过程忽略了AP设备性能对算法的不确定影响;参考点设备使用vivo X9i手机作为数据采集移动终端,每个参考点都经过100次测量,构成原始位置指纹向量,实验仿真在MATLAB R2014a上完成。 实验场所的局部测量结果如表1所示,把其中的测量数据作为初始位置指纹向量,通常情况下表中的数据不用经过处理即可作为初始实验数据用来算法研究。 实验数据采集100次,去噪过程设定检出水平为0.1,那么置信概率P=0.9,则格拉布斯表给出的临界值Gp(n)=3.017。 图3 RSS数据采集位置 实验数据经过去噪归一化处理后,有放回地随机抽取36次,构成36个训练集计算回归模型。 每一棵决策树的构建都经过GBRT算法处理,由多棵二叉树迭代的方式去替代一棵决策树,每棵决策树都是学习上一棵决策树的残差,避免了单棵决策树出现过拟合现象,最终形成一个强学习器模型。 实验过程采用定位精度和平均定位误差SE(Standard Error)作为评判指标来比较5种室内定位算法。原始位置指纹向量在核主成分提取,即根据式(16)得到特征空间为五维和十二维的数据矩阵,如表2和表3所示。 表1 进行100次采集的原始指纹数据库RSS 单位:dBm 表2 特征空间五维的数据库 表3 特征空间十二维的数据库 在室内定位算法中,AP数量是衡量室内定位算法性能的重要指标。一般情况下,AP数量越多,算法定位效果越好,平均定位误差越小。实验过程中,选取表1中前2~8个AP测量数据作为参考数据,KPCA算法将原始指纹映射到15维特征空间,IGBRT算法构建36个强学习回归模型,每个回归模型由15个二叉决策树组成。 图4是AP数量变化对平均定位误差的影响,从图中可以看出5种定位算法随着AP数量增多,算法平均定位误差越小。当AP数量为8时,KPCA-IGBRT算法的平均定位误差达到了1.16 m,明显优于1.51m的PCA-WKNN算法、1.43 m的SMN-PCA算法、1.29m的RVM-PLS算法和1.48 m的IGBRT算法。当AP数量从6增加7时,平均定位误差变化不大,原因可能是随着AP数量增多,引入更多的误差,对定位效果产生影响。 图4 平均定位误差随AP数量变化 表4为AP数量为8时,5种定位算法结果对比。从表中可知,本文算法在方差上能够提供相对可靠的数据。IGBRT算法在平均定位误差与SMN-PCA、RVM-PLS算法接近,但是方差较大,可能的原因是构建回归模型时,没有提取主成分,而是随机地采用RSS值。 表4 5种算法定位结果对比 单位:m 由图4可知,上述5种算法的平均定位误差在0.5 m~3 m,选取1.5 m来判断5种误差定位算法的准确度。图5是误差为1.5 m时5种算法的定位准确率情况,从图中可以看出5种算法用于定位的AP数量越多,在线定位精度越高,且本文算法明显优于其他4种算法。当AP数量为8时,本文算法在误差距离为1.5m的定位精度达到71.2%,相比于PCA-WKNN、SMN-PCA、RVM-PLS和IGBRT算法的48.8%,58.4%,61.1%和55.7%,分别提高了22.4%、12.8%、10.1%和15.5%。从图4和图5中可以看出,在相同的定位条件下,本文改进算法需要更少的AP数量。 图5 误差1.5 m的定位准确度 室内定位算法中,另一个影响算法定位性能的因素是各个测量点上无线信号强度的样本数量,它用来表示离线过程提取位置指纹向量特征信息消耗的时间。在定位精度相同的情况下,需要的无线信号强度的样本数量越少,表示此算法提取位置指纹特征信息需要的时间越少。 图6是在AP数量为8时,本文定位算法随不同RSS数量变化的定位情况,从图中可以看出5种定位算法的RSS样本数量越多,定位准确率越高。显然,当RSS样本数量达到20时,本文提出的算法定位精度已经达到57.8%,远远优于45.8%的PCA-WKNN算法、39.1%的SMN-PCA算法、51.2%的RVM-PLS算法和50.2%的IGBRT算法,而PCA-WKNN算法需要RSS样本数量为80时才可以与本文算法定位准确率相同,因此本文改进算法与5种算法相比,需要更少的RSS样本数量就可以达到更高的定位准确率。在RSS数量增多的情况下,定位准确率不是一味的提高,产生的原因可能是引入了更多的噪声,对定位结果造成影响。 图6 定位算法随不同RSS数量变化的定位情况 图7是定位精度随非线性特征空间维度Q的定位变化,从图中可以看出在特征空间维度Q增加的情况下,定位准确率也越来越高。当Q为16时,定位精度已达到0.85 m;当Q>16时,定位精度随Q的影响趋于稳定;当Q为22时,定位精度可达到0.82 m。 图7 定位算法随特征指纹空间维度的定位情况 表5是在AP数量为8,RSS样本数量为100,KPCA的特征空间维度为15时,各个模型离线训练和测试平均时间。从表中可以看出,离线训练时间PCA-WKNN算法最短达到26.752 s,IGBRT和KPCA-IGBRT算法次之,产生这种现象的原因是PCA-WKNN算法处理RSS计算量较小,IGBRT算法并行化方法训练多个回归模型;测试平均时间SMN-PCA算法最短达到0.034 6 ms,IGBRT和KPCA-IGBRT算法次之,但是SMN-PCA离线训练时间最长。综合离线训练和测试平均时间,IGBRT和KPCA-IGBRT算法最好,而KPCA-IGBRT算法比IGBRT算法定位误差更小,因此选取KPCA-IGBRT算法,在实际应用中效果更好。 表5 模型离线训练和测试平均时间 本文针对真实WLAN网络中无线信号强度易受环境等因素影响而产生的噪声问题,提出了一种基于KPCA和改进GBRT的室内定位算法。该算法在离线过程训练离线指纹数据库,得到离线强回归模型;在线阶段根据离线回归模型估测在线位置。实验结果表明,在相同的定位条件下,本文室内定位算法在AP数量、RSS样本数量等方面均优于PCA-WKNN、SMN-PCA、RVM-PLS和IGBRT 4种算法,在更少的AP和RSS数量的情况下,定位误差更小,且模型离线训练和测试平均时间相对更少,实际应用效果更好。本研究考虑到测试场所设备有限,不同型号的接入点和接收端设备都可能对无线信号强度获取产生不确定影响,并且整个实验过程的测试位置是不移动的,对可移动目标的定位情况尚需进一步深入研究。
1.2 KPCA算法提取核主成分

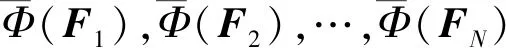

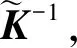


1.3 IGBRT算法构建回归模型
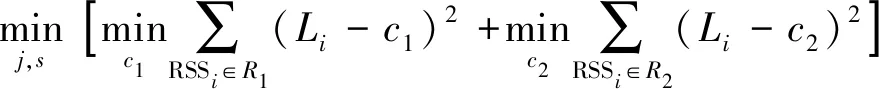

1.4 在线位置指纹处理
2 实验结果及仿真分析
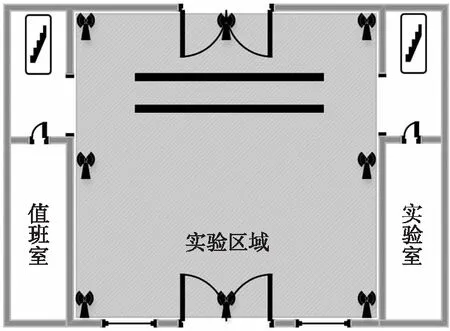
2.1 实验设置
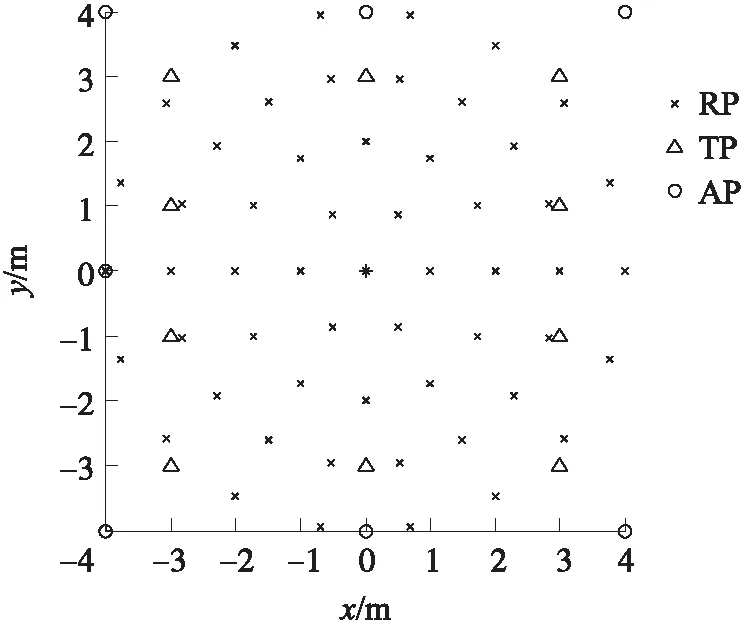

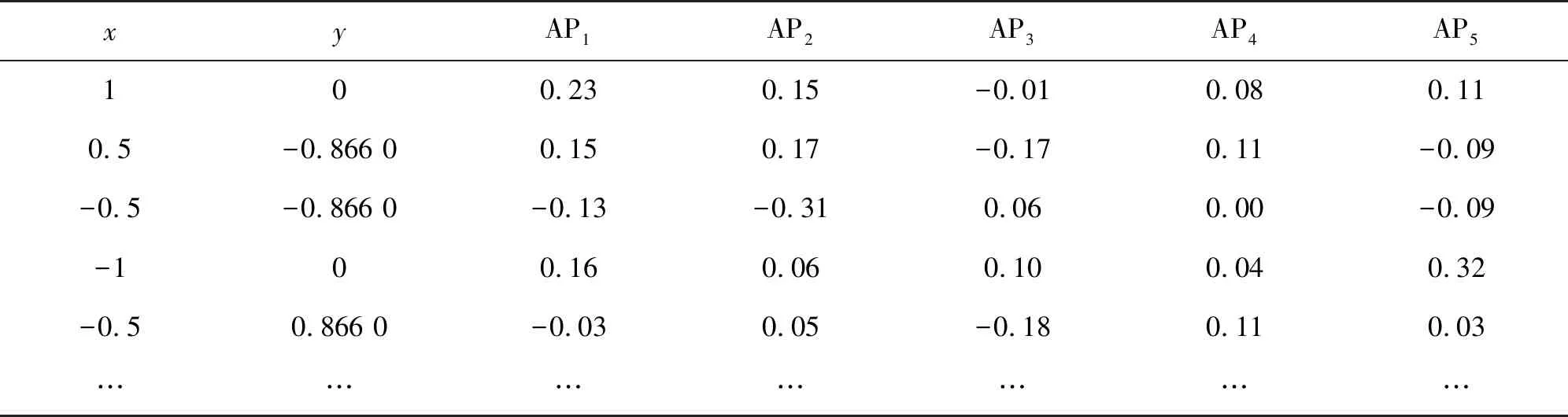

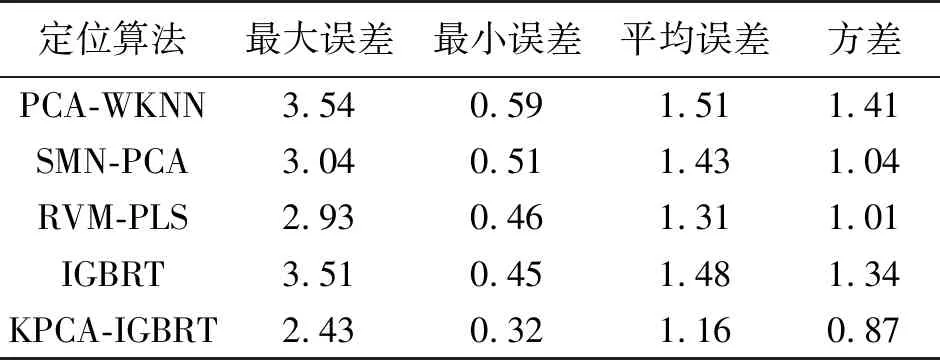
2.2 AP数量对算法性能的影响


2.3 离线阶段RSS样本数量对算法性能的影响

2.4 特征位置指纹空间的维度对定位算法的影响

2.5 模型离线训练和测试平均时间对算法的影响
3 结束语

