基于模糊支持向量机的合作频谱感知算法
南亚飞,马永涛,朱 芮,王煜东
(天津大学微电子学院,天津 300072)
近年来,认知无线电技术由于较高的频谱利用率而得到了越来越多的重视。通信设备使用认知无线电技术可以实时感知当前通信环境,智能快速的调整通信参数,并允许次用户SU(Second User)在主用户PU(Primary User)没有占用该频段时接入该频段通信,最大化频谱资源利用率[1-2],因此频谱感知准确度对认知无线电系统性能至关重要。
传统的频谱感知算法分为独立式频谱感知算法和合作式频谱感知算法。独立式频谱感知算法主要有三种:能量法、循环平稳检测法和匹配滤波器检测法[3-6];合作式频谱感知算法是在独立式频谱感知算法的基础上,各个SU将感知结果提交到融合中心FC(Fusion Center),并由FU通过某种规则计算得到频谱感知结果。判断规则主要分为两类:硬判决和软判决,硬判决:各个SU设备将感知结果(0或者1)传输给FU,由FU做出判断。论文[7]提出一种软化的硬融合算法,通过向FU传输两位数据(00,01,10,11),而不是(0,1)来提高频谱感知准确度。软判决:各个SU将感知数据传送到FU,由FU得出频谱感知结果。当SU和PU存在相对位置关系时,各个SU接受到的信号强度由于位置关系存在较大差异。相对于传统的合作频谱感知算法,基于机器学习的合作频谱感知算法由于学习特性可以有效的克服上述影响[8]。论文[9]提出一种基于非平行模糊支持向量机的合作频谱感知算法。论文[10]提出在支持向量机SVM(Support Vector Machine)训练阶段结合数据矩阵的特征值来提高分类准确度。论文[11]提出在合作频谱感知的过程中使用多级SVM训练样本,提高检测率。论文[12]联合遗传算法和SVM来提高低信噪比情况下频谱感知准确度。论文[13]提出了一种基于SVM的粒子群优化算法(PSO-SVM)来获取非线性阈值的新方法,以取代传统能量检测法中使用的线性阈值。
将SVM应用于频谱感知的主要原因:①SVM和频谱感知都是将数据分为两类:SVM是根据数据点与分类超平面的相对位置将数据分为两类,合作频谱感知是将感知频段分为未被PU占用和已被PU占用两种情况。②用于SVM训练和分类的数据向量是合作频谱感知中各个SU在单位时间内感知到的信号强度组成的能量向量。③在复杂多变的通信环境下,SVM由于良好的学习特性,可以有效提升频谱感知准确度。
在将SVM用于合作感知的过程中,所有的数据点对于分类面的确定权重是一样的,但在SU和PU分布在二维空间中且存在相对的位置关系时,噪声和野点对数据分类超平面的影响较大。为了解决训练数据点对分类面的确定权重相同的问题,本文研究了基于模糊支持向量机FSVM(Fuzzy Support Vector Machine)的合作频谱感知算法。FSVM是SVM的变体,增加了隶属度参数,每个数据向量的隶属度参数表示该训练数据点对分类面的贡献程度大小[14]。笔者使用K-近邻(KNN)[15-17]算法的思想计算出训练向量的隶属度参数(权重),称使用KNN计算隶属度的FSVM算法为K-FSVM算法。在训练阶段,数据点和该数据点的隶属度参数通过FSVM训练得到分类超平面。在判别阶段,通过比较待分类数据与分类超平面的相对位置,得到待分类数据分类结果。
本文的结构如下:第一部分介绍系统模型;第二部分介绍基于位置信息的合作频谱感知算法;第三部分介绍基于K-FSVM的合作频谱感知算法;第四部分进行仿真验证和结果分析;第五部分总结全文。
1 系统模型
1.1 认知无线电模型
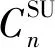

(1)
1.2 基于位置信息的能量向量
假定频段带宽ω,感知时长τ,采样个数ωτ,Zn(i)代表SUn的第i个采样值。信号采样值由所有通信中的PU信号采样和高斯噪声组成:
(2)
hm,n表示从PUm到SUn的信道增益,Xm(i)表示PU的传输信号,Nn(i)表示SU接收到的高斯噪声。Yn表示SUn的能量值:
(3)
所有的SU传输自己感知到的能量值到FU,FU组成能量向量:
Y=(Y1,…,YN)T
(4)
Yn服从自由度为q=2ωτ的非中心卡方分布,非中心参数:

(5)

(6)
‖·‖表示欧几里得距离,PL(d)=d-α表示距离为d,路径损失参数为α的路径损失,ψm,n表示阴影衰落,νm,n表示多径衰落。本文中假定PU和SU是静态的,阴影衰落和多径衰落在采样过程中都是静态(ψm,n和νm,n不变)。
如果采样样本的数目足够大,可以认为能量值Yn服从高斯分布,均值和方差分别为:

(7)

(8)
1.3 基于FSVM的合作频谱感知模型
频谱感知算法的目的是基于给定的能量向量Y,正确的判断频段的可用性A。算法实质是建立能量向量Y和频段可用性A的正确映射关系。基于SVM的合作频谱感知算法可以计算出基于能量向量的频谱感知分类超平面。首先使用有标签的能量向量对分类器进行训练,y(l)表示第l个训练向量,a(l)表示能量向量y(l)的频段可用性。通过训练器,得到分类面超平面参数。基于学习的频谱感知算法一般分为两个部分:训练阶段和分类阶段。基于非监督式学习的频谱感知算法,例如K-means算法,训练阶段通过训练将训练数据分为K类,并得到每一类数据的数据中心点,分类阶段通过比较待分类数据点和各个类别数据中心点的距离得到分类结果。基于监督式学习的合作频谱感知算法,例如SVM算法,训练阶段通过对已分类的能量向量的学习,找到最优分类超平面,分类阶段通过比较待分类数据点和分类面的相对位置,得到数据点的分类结果。

图3 情景a和b中能量向量的分布
图1是基于机器学习的合作频谱感知算法系统模型,由训练模块和分类模块两部分组成。

图1 合作频谱感知系统模型
训练模块的优势在当PU的传输参数发生变化时,训练模块可以智能快速的调整分类器参数。同时,频段环境发生变化时,训练模块通过再次训练得到最优的分类器参数。
2 基于位置信息的合作频谱感知
分类器根据通信环境和PU的情况自适应的调整参数,得到最优的分类超平面。训练阶段不需要任何关于信号的先验信息。并且,学习的优势使得当频谱环境发生变化时可以通过重新训练分类器,更新分类器参数。
基于机器学习合作频谱感知算法较传统的合作频谱感知算法有更优的感知准确度。当SU和PU分布在二维空间下,能量向量较为复杂,使用传统的合作频谱感知算法感知效果不理想。图2表示PU和SU分布的两种假设。

图2 认知用户位置假设
当SU和PU的分布情况如上图所示时,采样个数ωτ=2 000,使用式(3)计算接受到信号能量值。SU1采集到的能量值Y1和SU2采集到的能量值Y2组成能量向量Y=(Y1,Y2)T。数据点分为两类:频段可用的数据点和频段不可用的数据点。
图3是在图2的两种假设下SU1和SU2接收到的能量向量分布图以及使用学习算法确定的分类面(图中分类线),分类面将数据平面分为俩部分,频段被占用和频段未被占用。图3中的分类面由SVM算法计算得出。图3(a)和图3(b)信噪比设定为 -8 dB,图3(c)和图3(d)的信噪比-10 dB。图3(a)和图3(c)的场景设置为图2假设a,图3(b)和图3(d)的场景设置为图2假设b。
对比图3(a)和图3(c),在相同的场景下,信噪比越高,能量向量的分离度越高,两类向量的交叉部分越少。对比图3(a)和图3(b),相同的信噪比情况下,场景a的PU个数多,SU感知到的能量值较高,不同类数据点的分离度更高。
3 基于FSVM的合作频谱感知算法
基于K-FSVM的合作频谱感知算法系统模型如图4所示。

图4 基于K-FSVM的合作频谱感知算法框图
3.1 隶属度参数
3.1.1K-means求解隶属度

算法1使用K-means确定能量向量中心点
1:初始化中心点{ζ1=y(1),ζ2=y(2)}
2: whileck在上一次迭代中有改动
do
3:y(i)∈c1if ‖y(i)-ζ1‖<‖y(i)-ζ2‖
elsey(i)∈c2i=1,2,…,L
(9)
(10)
6: end while
使用K-means算法求隶属度参数:使用算法1中的伪代码得样本的中心点,则该类样本点距该类中心点的最大距离:
dk=MAX‖ζk-y(l)‖y(l)∈ck
(11)
求解度参数:
(12)
3.1.2KNN求解隶属度
KNN算法是一种基于最近邻和多数表决的监督式学习方法。KNN算法的核心目标是是找出与待分类样本距离最近的K个训练样本,并以这K个训练样本中大多数所属的类别作为最终的分类结果。KNN算法的核心是聚类,类似特征空间中基于投票原则的硬融合算法。首先寻找到训练样本集中K个距离最近的训练样本,信道不可用H1的数据点个数K1,信道可用H0的数据点个数K0,K1+K0=K。隶属度sl:
(13)
使用KNN计算隶属度参数的流程如算法2所示。
算法2使用KNN求解隶属参数
1:初始化K值和隶属度矩阵Sl=(s1,s2,…,sL)
2:fori=1:L
3: forj=1:L
4: if(j!=i)
5: 计算数据点与各个训练数据之间的距离
dij=‖y(i)-y(j)‖
6: end if
7: end for
8: 按照距离的递增关系对dij进行排序
9: 取距离最小的K个点D=(di1,di2,…,diK)
10: 根据式(13)得到该数据点隶属度si
11: end for
12: 输出隶属度矩阵
3.2 SVM
SVM的目标是找到最优的线性分类面,但能量向量一般是线性不可分,将能量向量通过非线性变换映射到可分的高维特征空间。不同类别能量向量满足:
(14)
ω表示权重向量,ω0表示偏置,a(l)是y(l)的频段可用新信息。上式中数据在高维空间的分类超平面大多数情况下不是一个严格的线性分类面,所以引入松驰标量δ(l),上式变为:
a(l)[ωφ(y(l))+ω0]≥1-δ(l)
1≥δ(l)≥0l=1,…,L
(15)
式(14)中两个式子分别代表的两个超平面。为了得到最优的分类超平面,要求两个超平面之间距离最大。2/‖ω‖2为超平面之间距离,最优超平面的求解转化为:
(16)

(17)
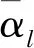
3.3 FSVM用于合作频谱感知
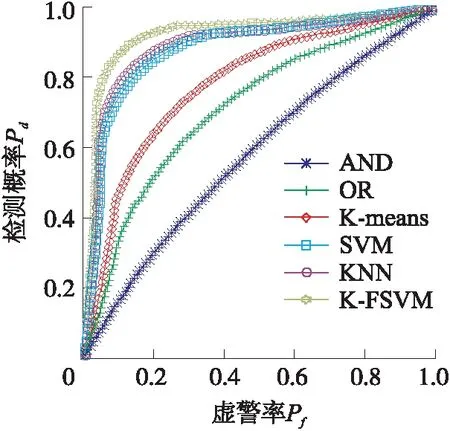
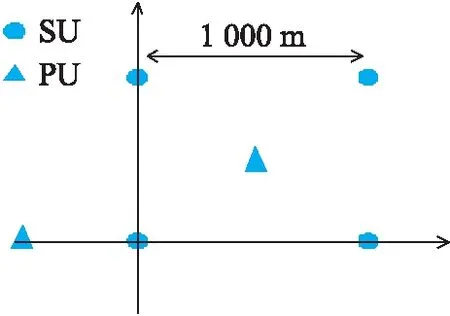
标准SVM是对所有的输入样本数据同等对待,对噪声点很敏感。FSVM对每个样本引入一个模糊隶属度参数。隶属度参数代表每个样本对分类超平面的贡献程度大小,与传统SVM相比,FSVM能更好地克服噪声点和野点的影响,提高分类精度。引入的模糊因子sl(0 (18) 式中:C为常数,整体的求解过程和标准SVM相似,通过构造拉格朗日函数,得到上式的对偶规划: (19) αi的约束上界与模糊因子si有关。整体求解过程与SVM类似。 假设SU和PU如图5所示分布在二维空间中,其中SU共9个,呈现3×3均匀分布。仿真参数设置如下:带宽ω=2 MHz,感知时间τ=100 μs,路径损失参数α=4,假设阴影效应和多径衰落参数ψm,n=1,νm,n=1,感知过程中阴影效应和多径衰落为准静态。设置PU的位置PU1为(-500,0)和PU2为(500,500)。每个PU占用频段通信的概率为0.5,各个PU相互独立。PU1和PU2都不占用频段通信的概率v(0,0)=0.25;PU1不占用频段,PU2占用频段通信的概率v(0,1)=0.25;PU1占用频段,PU2不占用频段通信的概率v(1,0)=0.25;PU1和 PU2都占用频段通信的概率v(1,1)=0.25。 图5 认知网络空间二维分布(3×3) 图7 信噪比-8 dB情况下各算法ROC曲线 图6和图7比较了在信噪比分别为-10 dB和 -8 dB,认知用户的阵列为3×3共9个SU和2个PU的情况下,基于K-FSVM的合作频谱感知算法、基于SVM的合作频谱感知算法、基于KNN的合作频谱感知算法、基于K-means的合作频谱感知算法、基于OR准则的合作频谱感知算法和基于AND准则的合作频谱感知算法的ROC曲线图。 图6 信噪比-10 dB情况下各算法ROC曲线 如图6和图7所示,基于K-FSVM的合作频谱感知算法性能最优,基于KNN的合作频谱感知算法在信噪比为-8 dB的情况下性能优于基于SVM的合作频谱感知算法性能。但在在信噪比为-10 dB的情况下,基于KNN的合作频谱感知算法和基于SVM的合作频谱感知算法性能非常接近,KNN算法更多考虑数据在空间中的分布,利用聚类特性完成分类任务。基于监督式学习的合作频谱感知算法(例如K-FSVM、KNN、SVM)要优于基于非监督式学习的合作频谱感知算法(例如K-means),而基于学习的合作频谱感知算法要优于传统的合作感知算法。 随着信噪比的增加,两类数据点的分离度越高,噪声引起的不确定性降低,频谱感知算法的性能也随之增加。基于机器学习的合作频谱感知算法随信噪比增加,ROC曲线的变化程度优于传统的合作频谱感知算法。 用于训练的能量向量的维数为SU的个数N,SU的数量N决定了能量向量的数据维数。本小节研究SU的数量和分布对算法性能的影响。 图8 认知网络空间二维分布(2×2) 图9为当SU和PU分布如图8所示,在信噪比为-10 dB,SU的个数为2×2共4个,PU的个数为2的情况下各算法的ROC曲线对比图。 图9 信噪比-10 dB情况下各算法ROC曲线 图9和图6相比,当SU数目减少时(能量向量维数下降),能量向量内蕴含的信息也在减少,导致频谱感知系统性能下降。理论上,能量向量维数越高,分类效果越好。但N的增大意味着资源的消耗。当N=1 时,就是使用学习算法的独立频谱感知算法,利用训练数据找到可以使感知效果最好的阈值,实质上是一个阈值最佳的能量法。当N=2时,据图3所示,分类超平面是一条曲线,将数据平面分为两部分。当N=3时,分类器是一个平面,当数据是N时,分类超平面是一个N-1维的特征向量,将特征空间分为两部分。N越大,特征空间维数越高,含有的信道信息越多,分类效果越好。特征空间维数越高,实质上是牺牲计算复杂度,获得较高感知准确度。 FSVM在训练的过程中,不同隶属度函数对感知系统性能影响较大,图10对比了使用KNN和K-means 算法作为隶属度函数时基于K-FSVM的合作频谱感知算法性能对比。 图10 不同隶属度的ROC曲线 图11 各算法检测概率随信噪比变化情况 如图10所示,使用KNN求解隶属度的感知算法性能优于使用K-means求解隶属度参数的感知算法性能。而且,随着SU的数目N的增多,能量向量维数增加,训练数据含有的信息越多,算法感知性能越好。 图11比较了在认知用户的阵列为图5的情况下基于K-FSVM的合作频谱感知算法、基于SVM的合作频谱感知算法、基于KNN的合作频谱感知算法的检测概率和虚警率随SNR增加的变化情况。 由图11可知,当SNR较低时,基于机器学习的合作频谱感知算法计算的分类超平面有较高的检测概率,一般会大于50%,但代价是虚警率也会较高。随着信噪比的增加,频段可用和频段不可用的训练数据分离度变高,基于学习的合作频谱感知算法的检测变高,同时虚警率也降低。当信噪比大于-5 dB时,检测概率已经到达100%,同时虚警率为0%。 当SU和PU分布在二维空间并存在相对位置关系时,笔者研究一种基于K-FSVM的合作频谱感知算法,算法首先通过KNN计算各个数据点的隶属度参数,通过FSVM训练得到分类超平面参数。仿真结果显示,在低信噪比的情况下,噪声对接收信号的影响较大,研究的基于K-FSVM的合作频谱感知算法优于基于KNN的合作频谱感知算法和基于SVM的合作频谱感知算法。基于机器学习的合作频谱感知算法优于传统的合作频谱感知算法。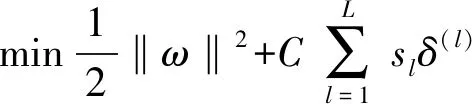
4 仿真分析

4.1 不同信噪比情况下各算法性能对比

4.2 不同认知用户分布情况下性能对比

4.3 隶属度函数对算法性能的影响

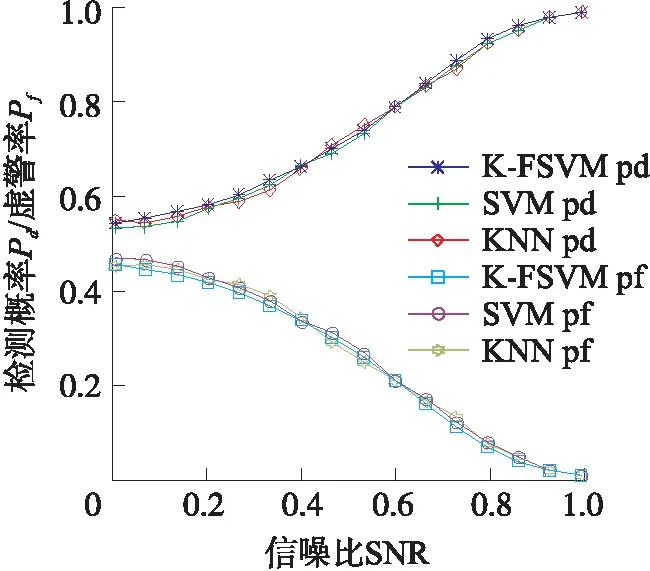
4.4 检测概率和虚警率随信噪比变化的比较
5 结束语

