基于Pancharatnam-Berry 相位和动力学相位调控纵向光子自旋霍尔效应*
刘金安 涂佳隆 卢志利 吴柏威 胡琦 马洪华 陈欢 易煦农
(湖北工程学院物理与电子信息工程学院,孝感 432000)
(2018 年11 月11 日收到; 2018 年12 月14 日收到修改稿)
提出了一种基于Pancharatnam-Berry 相位和动力学相位操控纵向光子自旋霍尔效应的方法. 理论分析表明: 当光场通过一个由Pancharatnam-Berry 相位透镜和动力学相位透镜构成的透镜组时,透镜组会存在两个自旋相关的焦点. 首先,当左旋和右旋圆偏振光通过微结构相位延迟为 π 的Pancharatnam-Berry 相位透镜时,由于Pancharatnam-Berry 相位的自旋相关性,两个圆偏振分量会获得符号相反的Pancharatnam-Berry 相位而导致其中一个被聚焦而另一个发散. 然后,在Pancharatnam-Berry 相位透镜后再插入普通透镜引入动力学相位调制,由于动力学相位是自旋无关,使得这一透镜组可以在合适的条件下使不同自旋态的光子分别聚焦于纵向上不同焦点处. 纵向自旋分裂由两透镜焦距及间距共同决定,因此可以通过改变两个透镜的焦距及其间距获得任意的纵向自旋分裂值. 最后,搭建了一套实验装置,所得实验结果与理论结果一致.
1 引 言
众所周知,光子具有自旋角动量. 光子的自旋角动量与其圆偏振手性有关,左旋和右旋圆偏振光子分别具有−ℏ和 +ℏ 的自旋角动量,其方向分别平行和反平行于光场的传播方向. 光子除了具有内在的自旋角动量之外,还有外在的轨道角动量(与光场的螺旋相位有关). 当光场的传播方向发生改变时,光子自旋角动量随之改变,总角动量守恒要求光子轨道角动量发生变化来补偿,从而使得自旋相反的光子在空间发生分离,这就是日本的Onoda等[1]首次提出的光自旋霍尔效应(spin Hall effect of light)的概念. 他们从理论上证明了光在不同介质的分界面上反射或折射时,会在垂直于介质折射率梯度的方向产生自旋分裂. 然而,光自旋霍尔效应导致的光场横向分裂值通常在波长的几分之一量级,难于直接观测. 2008 年,Hosten 和Kwiat[2]以及Bliokh 等[3]利用量子弱测量的方法首次实验验证了这一现象,引起研究者们对光自旋霍尔效应的极大兴趣. 理论研究表明: 光自旋霍尔效应导致的横向分裂值与入射光的波长、入射角及菲涅耳系数的比值等因素有关[4−13]. 因此,光自旋霍尔效应包含了界面材料的信息,可以通过界面材料调控光自旋霍尔效应,也可以利用光自旋霍尔效应来研究界面材料的特性[14,15].
导致光自旋霍尔效应的内在物理机制可以归结为两类几何相位. 其中一类几何相位被称为Ryto-Vladimirskii-Berry (RVB)相位. 它与光的传播方向有关,比如光在介质分界面发生反射和折射导致传播方向改变而产生的附加相位就是属于这一类相位. RVB 相位使光场的左、右旋圆偏振光分量在实空间(坐标空间)产生分裂. RVB 相位导致的自旋分裂往往非常小,需要采用弱测量技术或者经过多次反射才能观测到[2,3]. 另一类是Pancharatnam-Berry (PB)相位,它与光场偏振态的改变有关. 当傍轴光束通过非均匀各向异性介质时会获得一个空变的PB 相位,从而引起光场在动量空间(k空间)的自旋分裂. 由PB 相位导致的自旋分裂在实空间会随传输距离的增大而增大,从而获得大的自旋分裂值,可以被直接观测到[16−20].
基于PB 相位,研究者们设计了多种不同结构的超透镜(Metalens). Capasso 研究组[21]采用二氧化钛纳米片构建了一种可见光波段的PB 相位透镜,实现了亚波长超分辨成像. 湖南大学的Ke等[22]利用飞秒激光在平凸透镜的平面一侧写入PB 相位透镜,从而实现了PB 相位透镜和传统动力学相位透镜的集成. 关于光子自旋霍尔效应的研究,以往主要关注光场横向的自旋分裂,即两个分裂的自旋光斑位于光束质心的两侧[3,5−9],Shu 等[23]则研究了径向的自旋分裂. 陈敏等[24]结合PB 相位和动力学相位获得了横向平面内的任意自旋分裂.
我们在此前的研究中,也利用PB 相位和动力学相位实现了对光场偏振的操控,产生了具有混合偏振态的光束[25]. 本文将讨论利用PB 相位和动力学相位实现对光场的纵向自旋分裂的操控. 采用飞秒激光在石英硅中写入设计好的微结构,制作成基于PB 相位的透镜. 当线偏振光入射到超表面透镜时,其左、右旋圆偏振分量会分别获得符号相反的PB 相位,结果使得两个圆偏振分量一个会聚,一个发散. 理论分析和实验结果都证明PB 相位透镜结合基于动力学相位设计制作的常规透镜可以实现对光场纵向自旋分裂的任意调控.
2 理论分析
PB 相位与光场的偏振态变化有关,而波片是实现光场偏振变换的常用光学元件,这里先采用琼斯矩阵的方法分析波片对光场的变换. 波片的琼斯矩阵可以表示为

其中Γ表示波片的相位延迟,θ表示波片光轴与x轴的夹角. 假设一束圆偏振光正入射到波片,其琼斯矢量可以写为

其中σ=±1 ,+ 代表左旋圆偏振光,–代表右旋圆偏振光. 联合(1)和(2)式,得到输出光场为[26,27]
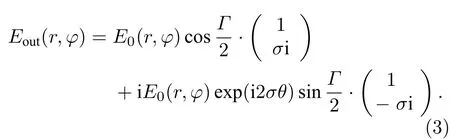
从(3)式可以看出: 输出光场由两部分叠加而成,第一部分与原入射光具有相同的圆偏振手性(自旋态),第二部分与原入射光的偏振手性相反. 这两部分光场的振幅完全由波片的相位延迟Γ决定. 如果Γ=π,则入射左旋(右旋)圆偏振光完全转化为右旋(左旋)圆偏振光,其偏振手性发生反转. 另外,尤其值得一提的是: 第二部分输出光还携带有2σθ的附加相位,这一相位就是由于偏振态改变而产生的PB 相位,并且PB 相位的符号由入射光的偏振手性决定. 同时,还注意到PB 相位与光轴方向有关,这意味着如果能够制作出一个光轴随空间坐标变化的器件,那么就可以使光场获得一个空变的PB 相位,从而实现对光场的波前整形及偏振调控.
本文采用飞秒激光在石英硅玻璃中蚀刻局域光轴方向随空间坐标变化的微结构来构建PB 相位透镜. 高强度的飞秒激光使纯石英玻璃(SiO2)分解为多孔玻璃(SiO2(1–x)+xO2),从而导致激光蚀刻过的地方产生形式双折射(form birefringence)[28,29]. 器件的局域光轴(快轴和慢轴)方向与激光蚀刻的微结构方向平行或垂直. 所以,这些激光蚀刻微结构实际上可以看作是一些微纳米尺度的波片. 显然,只要合理控制这些微结构的空间分布及相位延迟,就可设计得到基于PB 相位的透镜.
根据光学知识,普通透镜要使平面波聚焦在焦距为f的位置,其相位变换因子可以写为
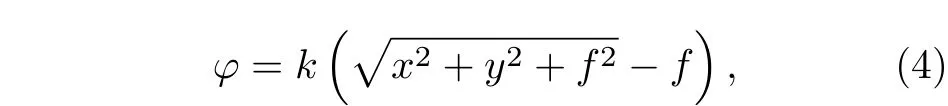
其中k为真空中的波数. 根据(3)式,对于左旋圆偏振光而言,要获得(4)式所描述的PB 相位,写入的微结构局域光轴方向必须满足
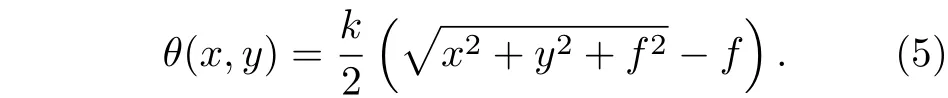
这里采用的PB 相位透镜的所有微结构均具有相同的相位延迟 π ,也就是说,这些微结构可以看作是一些微纳米尺度的半波片. 图1(a)给出了基于以上思路设计的PB 相位透镜的局域光轴分布示意图.
由(3)式可知: 由于微结构相位延迟为 π ,则通过PB 相位透镜左、右旋圆偏振光会分别获得符号相反的PB 相位,这意味着两个圆偏振光一个会被聚焦而另一个则会发散,自旋相反的光子在横向空间上被分离开来. 这其中内在的物理原因是PB 相位的自旋相关性. 所以,若要将不同自旋态的光子聚焦在纵向上不同位置处,可以引入自旋无关的动力学相位调控. 我们知道,普通透镜就是基于动力学相位设计的,因此,若在PB 相位透镜添加一普通透镜,则普通透镜的动力学相位调制可分别将左、右旋圆偏振光分别聚焦于不同焦点处,从而使得光子在纵向上实现自旋分离. 图1(b)给出了线偏振光通过PB 相位透镜和普通透镜组成的透镜组时不同自旋态光子的光路示意图. 假设PB 相位透镜的焦距为fPB,普通透镜的焦距为fC,则透镜组的焦点与普通透镜(lens)的距离可以表示为
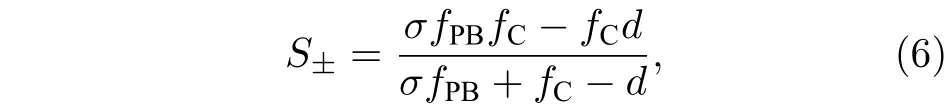
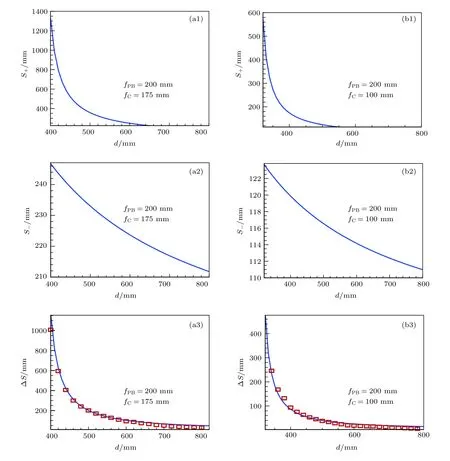
其中,+ ,–分别为左旋圆偏振、右旋圆偏振光的焦点位置;d为两个透镜之间的距离. 从(6)式可以看出: 透镜组存在两个自旋相关的焦点,当光场通过PB 相位透镜和普通透镜组成的透镜组时,不同自旋态的光子会聚焦在纵向上的不同焦点处,这就是纵向光子自旋霍尔效应. 按照前述设计而成的PB 相位透镜对左旋圆偏振光而言是一个正透镜,而对右旋圆偏振光而言则是一个负透镜. 所以,为确保右旋圆偏振光的焦点在普通透镜之后,传统透镜必须为正透镜. 通过分析(6)式可得到左旋圆偏振光具有实焦点的条件为:d>fPB+fC或d 图1 (a) PB 相位透镜的光轴分布示意图; (b)当线偏振光通过PB 相位透镜与普通透镜构成的透镜组时,不同自旋态光子的光路示意图; (c)实验装置示意图(GLP,格兰激光偏振镜; PB lens,PB 相位透镜; Lens,普通透镜; QWP,四分之一波片)Fig. 1. (a) Schematic illustration of optical axis spatial distribution of the PB phase lens; (b) optical pathway diagram of photon with different spin states when a linearly polarized light beam passes through the lens group consisting of a PB phase lens and a ordinary lens; (c) diagram of experimental setup (GLP,Glan laser polarizer; PB lens,PB phase lens; Lens,ordinary lens,QWP,quarter-wave plate). (7)式表明: 光子自旋纵向分裂由两个透镜的焦距及两个透镜之间的间距决定. 所以,通过调节两个透镜的焦距及两个透镜之间的距离即可方便地操控光子的纵向自旋分裂. 为了验证上述理论分析,设计了图1(c)所示实验装置. He-Ne 激光( 6 32.8 nm )产生的基模高斯光束通过准直系统(Collimator)扩束后入射到格兰激光偏振棱镜(GLP1). 光束被偏振棱镜转化为线偏振光后再入射到PB 相位透镜和普通透镜组成的透镜组,实现纵向光子自旋霍尔效应的调控. 为了测定输出光束的自旋态,在实验系统中引入四分之一波片(QWP)和另一个格兰激光偏振棱镜(GLP2)组合在一起来测量光场的斯托克斯参数S3. 最后,电荷耦合相机(CCD)用来测定光场强度分布. 图2 透镜组的焦点位置及纵向自旋分裂与两透镜之间的距离d的关系曲线 (a1)—(a3)分别为当f PB =200 mm ,fC =175 mm 时,透镜组的左旋圆偏振光焦点位置、右旋圆偏振光焦点位置及纵向自旋分裂与两透镜之间的距离d的关系曲线,(a3)中的实线为理论计算结果,方形离散点为实验测得的结果; (b1)—(b3)为f PB =200 mm ,f C =100 mm 时对应的结果Fig. 2. Focus position of the lens group and longitudinal spin splitting change with the distance of the PB lens and the ordinary lens,when (a1)−(a3)f PB =200 mm ,f C =175 mm; (b1)−(b3) the corresponding case,whenf PB =200 mm ,f C =100 mm. 图2 (a1)—(a3)为透镜组的焦点位置及纵向自旋分裂与两透镜距离d的关系曲线,其中PB 相位透镜的焦距取值为 2 00 mm ,普通透镜的焦距为175 mm. 图2(a1)和图2(a2)分别为根据(6)式得出的左、右旋圆偏振光焦点位置随两透镜之间的距离d变化的曲线. 图2(a3)为纵向自旋分裂与两透镜之间的距离d的变化关系曲线,其中实线为理论计算结果,方形离散点为实验测得的结果. 实验结果与理论值符合得很好. 从图2(a3)可以看出: 当两透镜之间的距离d>fPB+fC时,纵向自旋分裂随d的增大而减小. 所以,当调节透镜之间的距离d接近两透镜的焦距之和时,可以获得大的纵向自旋分裂; 而当d取值变大时,纵向自旋分裂迅速变小; 当d取值无穷大时,纵向自旋分裂趋于零.图2(b1)—(b3)为PB 相位透镜的焦距取 2 00 mm ,普通透镜的焦距取 1 00 mm 时,透镜组对应的焦距位置及纵向自旋分裂与两透镜距离d的关系曲线,从中可以看到与图2(a1)—(a3)相似的结论. 同时也注意到当fC分别取 1 75 ,1 00 mm ,而fPB取相同值时,纵向自旋分裂也是不同的. 分析光场偏振的有效方法是测定其斯托克斯参数. 这里,为了得到透镜组第一焦点F1和第二焦点F2处光场的圆偏振手性,在实验系统中引入一个四分之一波片(QWP)和另一个格兰激光偏振棱镜(GLP2)来测定其斯托克斯S3参数.S3参数定义为 其中,I(α,β)为CCD 测得的光强分布;α,β分别为QWP 光轴、GLP2 透光方向与x轴的夹角. 图3给出了透镜组焦点处光场的归一化斯托克斯参数s3=S3/S0,其中S0为CCD 直接在普通透镜后测得的光强分布. 图3(a)和图3(b)分别为第一焦点F1和第二焦点F2处的斯托克斯参数. 从图3 可以看出:F1处斯托克斯参数的值为−1 ,所以此处光场为右旋圆偏振光;F2处斯托克斯参数的值为 + 1 ,所以此处光场为左旋圆偏振光. 实验结果证明了不同自旋态的光子分别聚焦于焦点F1,F2处,这与前面的理论分析是一致的. 综上所述,由于PB 相位具有自旋相关性,所以当光场通过PB 相位透镜时,不同圆偏振的手性会呈现相反的聚焦特性(即会聚或发散),而当引入适当焦距的动力学相位透镜(普通透镜)后,可以让不同自旋态的光子分别聚焦在纵向上不同的焦点处. 纵向自旋分裂由PB 相位透镜的焦距fPB、动力学透镜的焦距fC及两透镜间的距离d共同决定,故而可以通过调节这三个参数、尤其是两透镜的距离d(更方便)来获得任意的纵向自旋分裂. 图3 透镜组焦点处光场的归一化斯托克斯s3 参数(a)焦点F 1处光场的斯托克斯s3参数; (b)焦点F 2 处光场的斯托克斯s3 参数Fig. 3. Normalized Stokes parameters3 of the optical field at the focus: (a) The Stokes parameters3 of the optical field at the focusF 1; (b) the Stokes parameters3 of the optical field at the focusF 2 . 本文提出了一种基于PB 相位和动力学相位调控纵向光子自旋霍尔效应的方法. 由于PB 相位的自旋相关性,所以,当左旋和右旋圆偏振光通过PB 相位透镜后会获得符号相反的PB 相位,使得一个圆偏振分量被聚焦,而另一个发散,使得不同自旋态的光子在横向上分离开来. 再插入一个普通透镜构成透镜组. 理论分析表明: 由于普通透镜引入自旋无关的动力学相位调制,当光场通过该透镜组时,在合适的条件下,左旋和右旋圆偏振光分别会聚焦在透镜组后不同位置,即透镜组有两个自旋相关的焦点. 这两个自旋相关焦点的存在,使得不同自旋态的光子在纵向上分离开来. 自旋分裂值由PB 相位透镜的焦距、动力学透镜的焦距及两透镜的间距共同决定. 所以,通过调节这三个参数即可获得纵向任意自旋分裂. 最后,搭建了一套实验装置对理论结果进行了验证,实验结果与理论分析完全一致. 我们相信这些结果可以加深对光子自旋霍尔效应的内在物理机制的理解,也有助于开发基于光子自旋霍尔效应的新型光子学器件.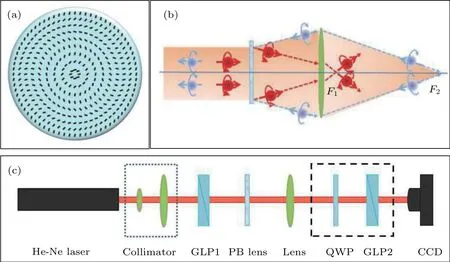
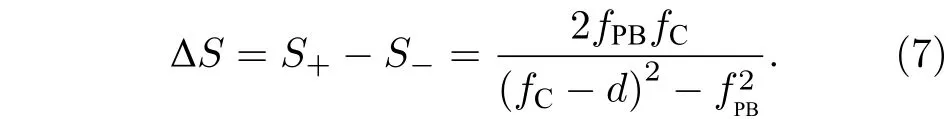
3 实验结果
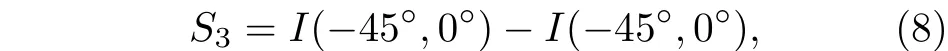

4 结 论

