Co-Al-W 基高温合金的团簇成分式*
马启慧 张宇 王清 董红刚 董闯
(大连理工大学,三束材料改性教育部重点实验室,大连 116024)
(2018 年5 月28 日收到; 2019 年1 月15 日收到修改稿)
Co-Al-W 基高温合金具有类似于Ni 基高温合金的γ +γ′ 相组织结构. 根据面心立方固溶体的团簇加连接原子结构模型,Ni 基高温合金的成分式即最稳定的化学近程序结构单元可以描述为第一近邻配位多面体团簇加上次近邻的三个连接原子. 本文应用类似方法,首次给出了Co-Al-W 基高温合金的团簇成分式. 利用原子半径和团簇共振模型,可计算出Co-Al-W 三元合金的团簇成分通式,为[Al-Co12](Co,Al,W)3,即以Al 为中心原子、Co 为壳层原子的[Al-Co12]团簇加上三个连接原子. 对于多元合金,需要先将元素进行分类: 溶剂元素—类Co 元素 (Co,Cr,Fe,Re,Ni,Ir,Ru)和溶质元素—类Al 元素 (Al,W,Mo,Ta,Ti,Nb,V 等); 进而根据合金元素的配分行为,将类Co 元素分为 (Cr,Fe,Re)和 (Ni,Ir,Ru); 根据混合焓,将类Al 元素分为Al, (W,Mo)和 (Ta,Ti,Nb,V 等). 由此,任何多元Co-Al-W 基高温合金均可简化为 伪二元体系或者伪三元体系,其团簇加连接原子成分式为(或其中,γ 与γ′ 相的团簇成分式分别 为(或和(或例 如,Co82Al9W9 合金的团簇成分式为[Al-Co12]Co1.1Al0.4W1.4 (~[Al-Co12]Co1.0Al0.5W1.5),其中γ相的团簇成分式为[Al-Co12]Co1.6Al0.4W1.0 (~[Al-Co12]Co1.5Al0.5W1.0),γ′ 相 的 团 簇 成 分 式 为[Al-Co12]Co0.3Al0.5W2.2 (~[Al-Co12]Co0.5Al0.5W2.0).
1 引 言
Ni 基高温合金[1]优异的高温性能源自由γ/γ′两相构成的微观结构,其中金属间化合物L12-Ni3Al(γ′ )以立方形态在面心立方结构的Ni 基体(γ)中共格析出. 2006 年,Sato 等[2]在Co-Al-W 三元系中发现了类似的结构特征,即L12结构的金属间化合物Co3(Al,W)在γ-基体中以立方形态共格析出. 这种新型γ′ 相强化的Co 基高温合金拥有与第一代Ni 基单晶高温合金相媲美的蠕变性能,流变应力随温度同样存在异常变化阶段,并且其合金熔点较Ni 基高温合金高50—100 K. 但由于在Co-Al-W 三元相图中,γ/γ′ 两 相区间十分狭小,γ′相热稳定性差,所以高温强度与Ni 基高温合金相比仍有差距.
通过合金化可以扩大γ/γ′ 两相区,从而有效提高γ′ 相 固溶温度,这类γ/γ′ 合金逐渐发展为多元复杂成分体系. Sato 等[2]以及Suzuki 和Pollock[3]发现,Ta 是γ′ 相强稳定元素,通过添加Ta 元素可以使Co79.4Al8.8W9.8Ta2(全文统一采用原子百分比表述,at.%)合金的γ′ 相固溶温度与硬度值明显高于Ni 基高温合金Waspaloy,Nb 和Ti 有相似作用. Bauer 等[4]发现,含B 合金的蠕变强度可与Ni基高温合金IN713C 相媲美,在此基础上添加2 at.%Ti 可以使该合金蠕变强度更好,接近于IN100 高温合金. Klein 等[5]发现,Cr 提高合金抗氧化性能,但过多添加则会破坏γ/γ′ 两相结构,此时需添加一定量的Ni,Mo 或Ta 来稳定γ′ 相. Ooshima 等[6]利用热力学计算发现,在多种合金元素中只有Re降低合金的γ′ 相固溶温度; 而通过实验验证后发现Nb,Ta 和Ti 确实会提高γ′ 相固溶温度. Chen和Wang[7]通过第一性原理计算发现,Mo,Ta,Ir 可以稳定γ′ 相. Bauer 等[8]在2010 年发现,W,Ta,Ti,Nb 和V 都会提高γ′ 相体积分数与固溶温度; 而W 含量的增加以及Ir 的添加都会提高合金的液相线温度. Kobayashi 等[9]通过实验发现,少量的Hf 添加可以稳定γ′ 相,而2.2 at.% Ta 的添加不会改变Co-Al-W 三元体系的相平衡. Meher 等[10]发现,相对于Co86Al7W7合金,Co59Al8W8Ni25合金中Ni 有强烈配分到γ′ 相 的趋势且γ基体中Ni的增加会提高其中W 的固溶度,在Co83Al10W5Ta2合金中Ta 的添加则降低Al 的配分系数; 关于原子占位,通过成分分析发现Ni 占据Co3(Al,W)中Co 的位置,而Al,W 和Ta 有相同的占位. 但是正如Ni 基高温合金一样,作为成分较为复杂的合金,Co-Al-W 基高温合金多元合金化存在着成分设计与优化的重大挑战,目前,基于电子空穴理论的相计算法[11]以及基于d 电子理论的新相计算法[12]都无法定量解决成分问题.
近期,Ni 基高温合金成分规律的研究有了重大进展,其核心突破在于引入了适用于描述合金固溶体化学近程序结构的“团簇加连接原子”结构模型[13−15]. 该结构模型认为,具有良好综合表现的固溶体合金是由特定的局域结构单元堆垛而成,每个单元覆盖最近邻配位多面体团簇以及次近邻的若干连接原子,可表述为团簇成分式: [团簇](连接原子). 对于具有高结构稳定性的单晶型Ni 基高温合金,其理想团簇成分式满足上横线元素表示同类元素的平均原子.
在此基础上,本文将该方法应用于Co-Al-W基高温合金的结构模型建立和成分解析. 下面首先介绍稳定固溶体的团簇加连接原子结构模型,确立基础的Co-Al 二元团簇结构单元,根据团簇共振模型结合γ和γ′ 两相晶格常数与合金元素半径计算连接原子个数,进而得到Co-Al-W 基高温合金的团簇成分通式. 然后将合金元素分类,置于团簇成分通式中,用于解析现有Co-Al-W 基高温合金成分. 最终根据解析结果和理论计算,确定Co-Al-W 基高温合金的理想团簇成分式为例如,Co81Al9W8Ta2合金的团簇成分式为[Al-Co12]Co1.0Al0.4W1.3Ta0.3(~[Al-Co12]Co1.0Al0.5(W,Ta)1.5). 最后,应用类似方法,确定了γ基体和γ′ 析出相的理想成分式,合金成分式为两者等比例混合而得.
2 固溶体的团簇加连接原子模型
众所周知,工业金属材料发展自固溶体合金,而由于对固溶体合金成分根源认识不足,具有优异性能的固溶体合金成分都是经过长期和大量经验式探索得到的.
固溶体合金是指在溶剂原子中溶入一定量溶质原子后仍保持溶剂结构特征的合金. 描述固溶体合金就是确定溶质在溶剂中的分布特征,也就是由于原子间相互的化学作用,在近程序局域范围,原子呈现出某种程度的有序行为,称为化学近程序结构.
人们发展了多种描述固溶体化学近程序的方法,包括Bragg 和Williams[17,18]的长程有序参数、Bethe[19]改进的短程有序参数以及Cowly[20−22]提出的短程序参量数,但这些参数都是从统计角度出发,没有建立结构模型,更无法解释合金成分规律.在前期工作中,我们提出了一种描述近程有序结构的方法,即团簇加连接原子结构模型,并且该模型已成功应用在准晶[23,24]、金属玻璃[25−28]和一些固溶体合金[29−33]中. 团簇加连接原子结构模型认为[34]:任何一个合金相的近程序结构都可以看作是由团簇加上位于团簇间隙中的连接原子组成,用团簇成分式可以表示为[团簇](连接原子),其中的团簇特指以中心原子为中心的第一近邻配位多面体,而连接原子则位于次近邻位置.
化学近程序只强烈地发生在最近邻和次近邻位置,以Ni-Cr-Al 基高温合金体系为例[34,35],其基体为面心立方固溶体 (γ) ,其最近邻团簇部分为配位数12 的立方八面体,次近邻最多有6 个原子,即连接原子个数的范围为1—6[36−38]. 团簇式结构单元体现了理想的化学近程序结构特征. 原子占位通常以混合焓为依据,即在Ni-Cr-Al 基合金中,与溶剂呈强负混合焓的元素,例如Al,优先置于团簇中心位置,余量进入连接原子位置,而作用较弱的仅置于连接原子位置,那么γ相的团簇式可以表述为(上横线元素表示同类元素的平均原子; Al, Cr 均与基体溶剂组元Ni 呈负混合焓;x,y分别表 示连接 原 子中Al 和的 原 子个数). 根据文献[34],单位团簇式中的原子个数Z表示为Z=c×ρa,c≈ 11.476 为无量纲常数,ρa表示平均原子密度 (单位体积原子∑个数,为平均原子体积的倒数,即有 1 /ρa=Va=fi×Vi,fi和Vi分别是元素i的原子分数和原子体积),r1表示团簇半径 (第一近邻的平均距离),这里r1=(RNi+RAl) (RNi和RAl分别是Ni 和Al 原子的半径).已知面心立方密堆率为0.74 (原子球体占总体积的比例),Ni-Cr-Al 固溶体的平均原子体积 1 /ρa及原子密度ρa为

将(2)式代入(1)式中,并代入原子半径值RAl=0.126 nm,RNi=0.125 nm,RCr=0.128 nm,得x,y之间的关系为

析出相γ′ 相具有AuCu3结构,为面心立方的完全有序结构,团簇依然为[Al-Ni12],而连接原子为3 个Al,达到理想相成分,团簇式为
3 Co-Al-W 基础体系的理想团簇成分式
Co-Al-W 基 合金 也以γ′ -C o3(Al,W) +γ-基体为结构特征,与Ni 基高温合金微观结构相似,且Ni 与Co 元素性质相近. 下面分别阐述两相及合金的理想成分式.
3.1 γ相的理想团簇成分式
在Co-Al-W 三元体系中,对于γ基体,合金化元素Al,W 和基体Co 均呈负混合焓 ( ∆HCo-Al=–19 kJ/mol,∆HCo-W=–1 kJ/mol),其中Al与Co的混合焓绝对值较大,故而占据团簇中心位置,过量Al 将占据连接原子位置; W 与Co 的混合焓绝对值较小,故而在有Al 占据团簇中心的情况下,W 占据连接原子位置. 因此Co-Al-W 固溶体合金γ的团簇成分通式为以Al 原子为中心原子的立方八面体团簇[Al-Co12]加上若干个Co,Al,W作为连接原子,即[Al-Co12](Co,Al,W)x,其 中[Al-Co12]团簇如图1 所示. 在添加合金化元素后,各种元素将按照原子相互作用规律进行分类而置入该基础成分通式,并通过计算确定连接原子个数.
按照文献[34]所提供的方法,将Co-Al-W 合金中γ相的化学结构单元设为[Al-Co12]CoxAlyWz,其中x,y,z分别表示连接原子位置中三种元素的原子个数,将三种原子半径代入(1)式,得到平均原子体积 (单位体积原子个数ρa的倒数)为

由Z=c·ρa以及r1=(RCo+RAl)可知,平均原子密度为
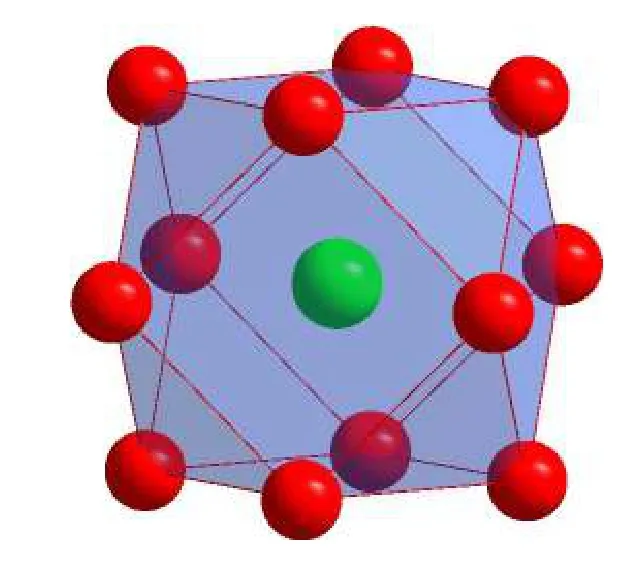
图1 Co-Al 基的面心立方固溶体及AuCu3 有序结构中的立方八面体[Al-Co12]团簇Fig. 1. Cuboctahedron [Al-Co12] cluster in Co-Al-base faced centered cubic solid solution and in AuCu3-type ordered structure.

将(5)式代入(4)式中,化简后得x,y,z之间的关系为

已知各原子的Goldschmidt 半径为RCo=0.125 nm,RNi=0.125 nm,RW=0.141 nm,RCr=0.128 nm[39]. 由于Co 与Al 之间存在强烈的相互作用,Al 原子呈共价半径RAl=0.126 nm[34]. 但是元素半径有可能在γ固溶体合金化后发生变化. 面心立方结构中晶格常数a与平均原子半径R之间的关系为对于多元合金,晶格常数可表示为每种元素半径Ri的原子百分比分数fi平均:

例如,对于合金Co82Al9W9,其γ相成分为Co81.7Al9.3W9.0,将上述各元素半径及其含量fi代入(7)式,则有γ相晶格常数a=(0.125 × 0.817 +0.126 × 0.093 + 0.141 × 0.090) ×= 0.3579 nm.γ相晶格常数的计算结果如表1 所列,可以看到,对于Co-Ni-Al-W 四元合金,根据(7)式计算所得的晶格常数值与各文献中实验所测值误差约为10–3量级,而其他合金的误差均在10–4量级,说明合金元素在固溶形成γ相时原子半径几乎无变化,故而下文计算时原子半径均使用RCo=0.125 nm,RW=0.141 nm,RAl=0.126 nm.
将Co,Al,W 原子半径代入(6)式,得x,y和z之间的关系为
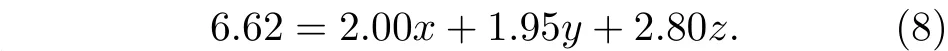
由(8)式得到连接原子总数为x+y+z=3.3–0.4z,通过分析γ相成分可知,连接原子中W 原子个数约为1,即z≈ 1,则x+y+z≈ 3,因此γ相的成分式含有三个连接原子.
3.2 γ′ 相的理想团簇成分式
在Co-Al-W 三元体系中,γ′ 相为具有固定成分式的金属间化合物Co3(Al,W),具有AuCu3结构. 据此,γ′ 相的团簇同样为[Al-Co12] (图1). 下面按照类似方法,根据原子半径与晶格常数计算连接原子个数.
首先判断合金元素的原子半径固溶到Co3(Al,W)中是否会发生变化. 根据文献[43]中的数据可知,Co3(Al,W)与Ni3Al 相的晶格常数分别为0.3565 nm 和0.3568 nm,这说明原子半径较大的W 原子加入后对γ′ 相的晶格常数并无过多影响,即W 原子半径变化最为明显. 根据γ′ 相成分及其晶格常数重新计算W 原子半径. 已知γ′ 相为γ相的超结构,其中类Al 原子(包括W)位于顶点位置,其平均原子半径为类Co 元素位于面心位置,其平均原子半径基本接近Co,则晶格常数a为

例 如,对 于 合 金Co82Al9W9,其γ′ 相成分为Co77.49Al10.03W12.48,将77.49 at.% Co,10.03 at.%Al 以及12.48 at.% W 代入(9)式,已知测得的γ′相 晶格常数为0.3594 nm,则W 的原子半径为– 2 × 0.125)/2–0.126 ×10.03/22.51] × 22.51/12.48 =0.1317 nm. 计算结果列于表2 中.

表1 实测的γ相成分和晶格常数[40−42],以及按照(7)式计算的晶格常数Table 1. Measured compositions and lattice constants ofγphase in Co-Al-W-base superalloys[40−42],in comparison with the calculated lattice constants.

表2 实测γ′ 相成分和晶格常数[40−42]以及根据(9)式计算的W 原子半径Table 2. Atomic radii of W fitted from measured compositions and lattice constantsγ′ phases in different alloys[40−42].
根据表2 所列结果的平均值,假设在γ′ 相中,W 原子的半径为RW=0.1316 nm,将Co,Al,W 原子半径代入(4)式,得x,y和z之间的关系为

由(10)式得到连接原子总数为x+y+z≈3.3–0.3z,通过分析γ′ 相成分,可知在连接原子中约有2 个W 原子,则x+y+z≈ 3,即γ′ 相的成分式亦含有三个连接原子.
综上所述,对于Co-Al-W 三元合金,其γ和γ′两相的团簇式中均存在3 个连接原子,说明其合金的基础团簇成分式必然为[Al-Co12](Co,Al,W)3,即与Ni 基高温合金[16]和马氏体不锈钢[32]的情形十分类似. 因此合金成分解析可以简单地用16 原子成分式进行,但实际的Co-Al-W 基高温合金往往含有多种其他合金化元素,因此首先需要进行元素分类,见下节.
4 合金元素分类
已知Co-Al-W 基高温合金的团簇成分通式为[Al-Co12](Co,Al,W)3,可以确定在团簇中存在三种不同的原子: 团簇中心原子、团簇壳层原子以及连接原子,显然基体溶剂元素Co 优先占据团簇壳层位置,而余量填入连接原子位置,并且由表1 和表2可知,γ基体相中的Co 明显多于γ′ 相. 在利用团簇加连接原子结构模型解析合金成分时,主要根据添加的合金化组元与基体组元之间的混合焓来判断其在团簇式中的位置. 由于Co 元素与Ni 元素性质相近,且有相同的原子半径,又因为Co-Al-W 基高温合金与Ni 基高温合金的微观组织极为相似,所以在对Co-Al-W 基高温合金中元素进行分类时,可以参考Ni 单晶高温合金,其元素分类以合金化元素与主要溶剂Ni 元素之间的混合焓为依据[16].
根据现有的Co-Al-W 基高温合金成分,向Co-Al-W 三元基体中添加的合金化元素有Ta,Ti,Nb,V,Cr 等,本文根据合金化组元与基体组元Co 之间的 混合焓 ∆H和合金元素在γ与γ′相之间的配分行为将合金元素进行分类,结果如表3所列.

表3 合金化组元与基体组元Co 之间的混合焓∆H(单位: kJ/mol)及在γ /γ′ 两相中的配分系数(K x=Cxγ′/Cxγ)[9,10,40−42,44−52]Table 3. Heats of mixing ∆ H(unit: kJ/mol)between alloying elements and matrix element Co and their partition coefficients (K x=Cxγ′/C xγ)forγandγ ′ [9,10,40−42,44−52].
合金元素首先分为两大类: 一类是溶剂元素,称为类Co 元素,用符号表示,包括Co,Ni,Ir,Ru,Cr,Fe,Re 等,它们均与Co 之间呈弱混合焓;另一类是溶质元素,称为类Al 元素,用符号表示,包括Al,W,Mo,Ta,To,Nb,V 等,它们与Co 呈负混合焓. 以此可以将Co-Al-W 基合金简化为伪二元合金体系,其团簇成分通式为
2) Al: 主要溶质元素,与Co 之间呈较强烈的负混合焓,其含量一般足以占据CN12 团簇的中心位置,是形成团簇的主要元素,构成八面体团簇,余量进入连接原子位置. 它同时强化固溶体γ和析出相γ′ ,在两相中的配分系数接近1.它与Co 只能形成亚稳γ′ 相 ,稳定的γ′ 相是通过添加W 来实现的[2].
特别地,Ni3Al 可以稳定存在,但是在Co-Al 相图中无稳定的Co3Al 存在,因此需要W,Mo 元素辅助Al 来稳定γ′ 相,这里的元素分类与Ni 基高温合金存在重大差别: W 和Mo 单独成为一类,其作用在于同Al 一起,共同形成稳定的γ′相,这也是Co-Al-W 基高温合金的独特之处,其他元素的分类与Ni 基高温合金一致.
下节利用推出的团簇模型和元素分类,分析现有典型Co-Al-W 基高温合金的成分规律.
5 Co-Al-W 基高温合金成分解析
5.1 合金成分解析原则及步骤
综上所述,根据面心立方固溶体的团簇加连接原子结构模型可知,Co-Al-W 三元合金以及γ和γ′相的团簇成分通式均为[Al-Co12](Co,Al,W)3,即包括16 个原子: 1 个位于团簇中心位置的中心Al 原子、12 个位于团簇壳层位置形成立方八面体团簇的Co 原子、以及3 个混杂占位的连接原子.
由此可以确定利用团簇加连接原子结构模型解析Co-Al-W 基高温合金成分的步骤为: 1)首先将原子百分比换算成在团簇式所占个数,即将原子百分比成分乘以0.16 ( =16/100),获得以Z=16团簇式为基础的成分式; 2)将元素归类后放置在团簇成分通式中相应位置,即得到该合金的团簇成分式.
以Co81.3Al9.2W9.5合金为例,此时已经表述为原子百分比,每个成分乘上0.16,得到在16 原子团簇式中分别有13.01 个Co、1.47 个Al 以及1.52 个W. 根据团簇模型,1 个Al 原子占据团簇中心位置,12 个Co 原子占据团簇壳层位置,其余原子均占据团簇与团簇之间的连接原子位置,即得到该合金的团簇成分式为: [Al-Co12]Co1.0Al0.5W1.5.
结合Co-Al-W 合金的团簇成分通式[Al-Co12](Co,Al,W)3与表3 中的合金元素分类,对现有的Co-Al-W 基多元合金的成分进行筛选,通过解析得到对应的团簇成分式,如表4 所列. 同时统计了符合条件的合金两相成分并进行解析,结果列于表5 中,筛选条件为: 1)合金中 Co 元素含量大于等于 50 at.%; 2)合金的微观组织中γ′ 相为立方形态; 3)合金的微观组织中γ′ 相的体积分数范围为 40% ≤Vγ′≤90%; 4)合金中只存在γ/γ′ 两相,无其他析出相; 5)合金时效温度为1173 K.

表4 Co-Al-W 基多元合金的团簇成分式,所列成分源自文献 [2−4,6,8,10,39,40−42,44,45,48,51,57−62]Table 4. Compositions formulas of Co-Al-W-base multi-element superalloys. The alloy compositions are taken from references [2−4,6,8,10,39,40−42,44,45,48,51,57−62].

表5 部分 Co-Al-W 基高温合金中γ 和γ′ 两相团簇式[40,42,44,45]Table 5. Composition formulas ofγandγ′ phases in some Co-Al-W-base superalloys[40,42,44,45].表5 部分 Co-Al-W 基高温合金中γ 和γ′ 两相团簇式[40,42,44,45]Table 5. Composition formulas ofγ andγ′ phases in some Co-Al-W-base superalloys[40,42,44,45].

图2 合金数量随 Co 含量的变化,虚线表示平均成分式Fig. 2. Statistical distribution of alloy compositions as a function of at.% Co. The dashed vertical line represents the ideal composition formula图2 合金数量随 Co 含量的变化,虚线表示平均成分式
Fig. 2. Statistical distribution of alloy compositions as a function of at.% Co. The dashed vertical line represents the ideal composition formula伪三元成分分布 (a) 合金成分; (b)γ和γ′ 两相成分; 图中虚线 为 Co-Al-W 三元相图中富Co端1173 K等温截面相图[2],中心成分点用蓝色空心三角形标出

图3 伪三元成分分布 (a) 合金成分; (b)γ和γ′ 两相成分; 图中虚线 为 Co-Al-W 三元相图中富Co端1173 K等温截面相图 [2],中心成分点用蓝色空心三角形标出Fig. 3. pseudo-ternary composition diagram:(a) Alloy compositions; (b)γandγ′ two phases compositions,where the dashed lines represent the isothermal section of the Co-Al-W ternary system in the Co-rich portion at 1173 K[2],and the blue hollow triangle points to the center composition图3
5.2 γ/γ′两相成分解析
类似地,分别绘制合金与两相的数量随Co 含量的变化图以及三元成分分布图,结果如图4 所示.
由图4 可知,γ相中 C o 含量范围为 84 at.%—88 at.%,γ′ 相中含量范围为 75 at.%—79 at.%.根据图4 中合金数量随Co 含量的变化趋势,可以统计出γ相的平均含量约为 85.85 at.%,对应含量 则 为 14.16 at.%,解析后其团簇式为统计出γ′ 相的平均含量约为76.37 at.%,对应含量则为23.63 at.%,解析后其团簇式为继而从相图中(或读出γ+γ′ 三角形双相区的三个端点 (图3(b)中由大环标注),分别为Co77Al9W14,Co78Al10W12γ′相区的两个端点)和Co85Al9W6(γ相区的最大固溶度). 根据前述方法,解析得到这三点的16 原子团簇成分式为[Al-Co12]Co0.3Al0.5W2.2,[Al-Co12]Co0.5Al0.6W1.9和[Al-Co12]Co1.6Al0.4W1.0,可以近似为[Al-Co12]Co0.5Al0.5W2.0(γ′ 析出相成分式)和[Al-Co12]Co1.5Al0.5W1.0(γ固溶体成分式).

图4 合金数量随类Co 元素总量 的变化 (a)γ 和 γ′相成分; (b) 合金成分; 竖虚线表示各自理想成分Fig. 4. Evolution of numbers of alloys with content:(a)γ ′andγphases; (b) alloys. Vertical dashed lines represent the ideal compositions.
此外,根据(8)和(10)式,当团簇式中连接原子中Al 的个数为0.5 时,对于γ和γ′ 两相分别有解(1.5,0.5,1)和(0.5,0.5,2),与上述实验结果相符,即得到γ固溶体理想团簇成分式为γ′ 析出相理想团簇成分式为而合金成分式正好为两者的等比例混合,即
6 结 论
金属间化合物-γ′ 析出强化的Co-Al-W 基高温合金具有与Ni 基高温合金相似的微观结构,结合前期获得的Ni 基高温合金的元素分类和团簇成分式,本文得到了Co-Al-W 基高温合金以及两相的成分式.
1) 根据合金中γ′ 和γ两相成分与晶格常数的实验结果,推断出W 的原子半径在γ′和γ两相中分别 为0.1316 nm 和0.141 nm (Goldschmidt 半径); Al 原子半径均为共价半径,即0.126 nm. 计算得到两相的团簇结构单元均为[Al-Co12]团簇加上3 个连接原子,进而可以推断出,合金的团簇成分通式为[Al-Co12](Co,Al,W)3;
2) 对于多元合金,共有溶剂及溶质元素两大类,前者为类Co 元素(Co,Ni,Ir,Ru,Cr,Fe,Re),后者为类Al元素(Al,W,Mo,Ta,Ti,Nb,V 等). 其中,溶剂元素可进一步分为(Cr,Fe,Re,配分系数小于1)和(Ni,Ir,Ru,配分系数大于1),溶质元素均倾向于形成γ′ 相,包含Al、类W 元素(W,Mo,与Co 之间呈弱于Al-Co 的负混合焓)和类Ta 元素(Ta,Ti,Nb,V 等,与Co 之间呈强于Al-Co 的负混合焓). 由此,任何复杂C(-Al-W 基合金均可表述为伪二元和伪三元体系;
3) 通过解析典型Co-Al-W 基合金成分,得到了合金的理想团簇成分式:(或即 以Al 为中心,Co元素作为第一近邻的立方八面体团簇加上3 个连接原子;γ相的成分式为相的成分式为(或

