洛仑兹破缺标量场的霍金隧穿辐射*
杨树政 林恺
1) (西华师范大学物理与空间科学学院,南充 637002)
2) (中国地质大学(武汉)地球物理与空间信息学院,地球内部多尺度成像湖北省重点实验室,武汉 430074)
3) (Escola de Engenharia de Lorena,Universidade de Sao Paulo,12602-810,Lorena,Sao Paulo,Brazil)
(2018 年11 月19 日收到; 2019 年1 月7 日收到修改稿)
把洛仑兹破缺的标量场方程推广到弯曲时空中,并通过Aether-like 项对标量场方程进行修正,该项所产生的效应也会影响到黑洞时空视界附近处的物理效应. 接着,进一步在半经典近似下得到了修正的Hamilton-Jacobi 方程,然后用这一修正的Hamilton-Jacobi 方程研究了史瓦西黑洞的隧穿辐射特征,并讨论了洛仑兹破缺对黑洞霍金辐射和黑洞熵的影响. 结果表明,形式的Aether-like 项的效应可能使黑洞温度增加,而黑洞熵降低. 该工作可以帮助我们更深刻地理解弯曲时空中的洛仑兹破缺效应的物理性质.
1 引 言
经典的黑洞是全黑的,因为没有任何经典粒子可以从经典黑洞内穿越出来达到无穷远的观测者处. 但是,当霍金考虑了黑洞视界附近的量子效应后,他发现黑洞可以发出量子辐射,这种辐射被称为霍金辐射[1,2]. 霍金辐射的存在使得黑洞热力学定律有了牢固的物理基础,因此把引力理论、量子理论和热力学及统计理论有效地联系起来[3−5]. 一个解释霍金辐射的简明理论是隧穿理论: 把黑洞视界视为一个势垒,经典粒子无法直接通过此势垒,但是由于量子隧穿效应的存在,黑洞视界内部的虚粒子有一定概率穿越黑洞视界这个势垒,并进一步实化为实粒子,这就是量子霍金辐射. 利用量子隧穿的观点,文献[6—14]提出隧穿辐射方法来计算黑洞温度和熵,随后文献[15,16]提出半经典的方法从弯曲时空的标量场方程推导出弯曲时空的Hamilton-Jacobi 方程,并用这个方程计算霍金辐射,这个方法大大简化了黑洞辐射的研究. 2008 年,Kerner 和Mann[17,18]开始思考用半经典的方法研究Dirac 场粒子的隧穿辐射,在这个方法中,他们把Dirac 粒子分为自旋向上和自旋向下两种情况,并进一步推导得到Dirac 粒子的隧穿辐射方程[19−24].本课题组[25−27]则提出新的方法来研究费米子隧穿辐射问题,在我们的方法中,Dirac 方程先通过半经典近似化为一个简明的矩阵方程,这个方程可以通过gamma 矩阵写成一个很简单的形式,接着根据gamma 矩阵的反对易特性,发现半经典的矩阵方程成立的条件正是标准的Hamilton-Jacobi 方程,接着按照标准的半经典Hamilton-Jacobi 方法可以推导出黑洞的费米子隧穿辐射特征. 该结果暗示了Hamilton-Jacobi 方法的内在一致性,其本质是体现了理论的洛仑兹对称性.
然而,在高能领域的研究中,量子引力的研究暗示洛仑兹不变性可能需要在普朗克尺度上被修正. 近来,一种洛仑兹破缺的标量场理论被提出,其作用量可以写为[28]

其中m是标量场的质量;λ是洛仑兹破缺项的比例常数,通常是一个小量;uα在平直时空中是一个类以太场的常矢量,本文将始终使用(–,+,+,+)的号差. 因此在平直时空中修正的标量场方程变为
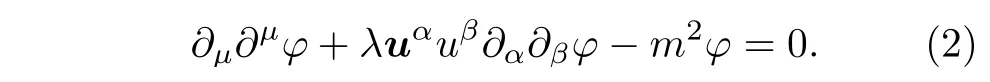
近来的工作对这种修正的标量场方程进行了深入探讨[28−32],发现在高能领域修正的标量场方程有许多独特的性质.
本文把洛仑兹破缺的标量场方程的工作进一步推广到弯曲时空,并进一步研究黑洞的霍金辐射. 在第2 节中,将首先给出弯曲时空中的洛仑兹破缺标量场方程,并进一步通过半经典近似把该方程化为变形Hamilton-Jacobi 方程; 接着在第3 节中,将具体计算在史瓦西时空背景下的修正的霍金辐射特征,得到修正的标量场隧穿辐射和修正的霍金温度; 第4 节给出讨论和结论.
2 洛仑兹破缺的标量场方程以及修正的Hamilton-Jacobi 方程
在正则坐标系的平直时空中类以太矢量是一个常量,因此自然满足关系
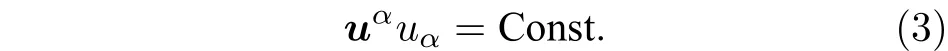
但是在弯曲时空中,为了满足(2)式的关系,不能简单把uα设为常量. 因此在弯曲时空中,考虑作用量
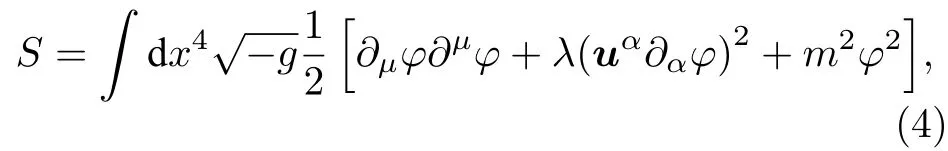
可以得到弯曲时空中的洛仑兹破缺标量场方程为

或者
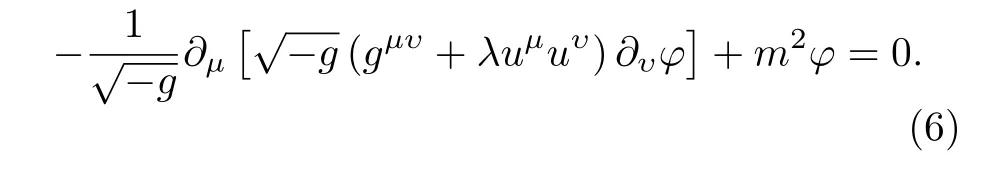
为了得到弯曲时空中的修正Hamilton-Jacobi方程,可以重写标量场波函数为
根据(3)式可以求得

所以把(7)式代入任意自旋的玻色子方程,把 ℏ 视为小量,并且只保留方程的零阶项,可以得到
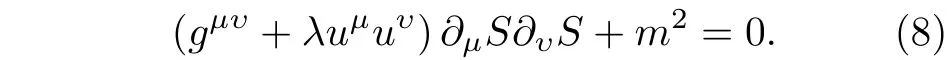
这正是修正的标量场粒子的Hamilton-Jacobi 方程. 第3 节将应用这个半经典的修正Hamilton-Jacobi 方程研究黑洞的霍金辐射特征.
3 史瓦西黑洞的隧穿辐射及其修正
史瓦西黑洞的逆变度规可以写为

其中

其中M是黑洞的质量,黑洞视界rh=2M. 这里分别讨论四种情况下的黑洞辐射. 由于作用量S可以写为

于是(8)式可以写为

为了求解上述方程,先考虑不同的uα情况:
1)uα=(ut,0,0,0) 情况这里c0是一个常数. 因此,通过(12)式可以把径向的Hamilton-Jacobi 方程写为

这里的C是分离变量常数,因此有

这里正负号分别代表出射模和入射模,在计算中,已经用到λ是小量的条件. 所以黑洞的隧穿辐射率是

其中,霍金温度是
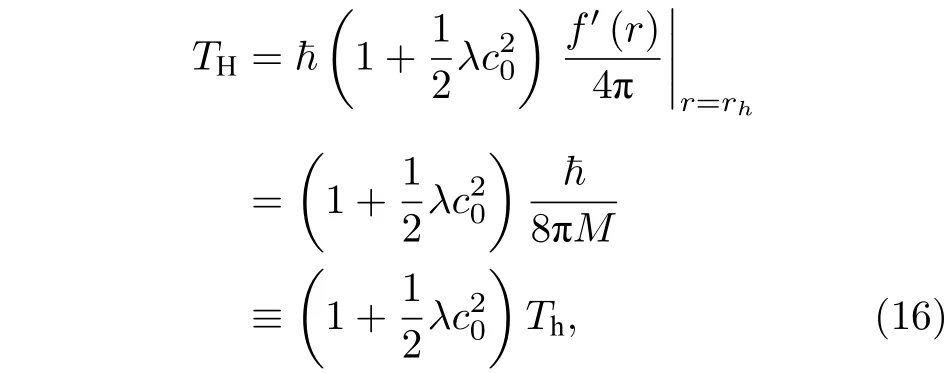
这里的Th是未修正的史瓦西黑洞事件视界处的霍金温度,而修正后的霍金温度TH则与/2 相关.
2)uα=(0,ur,0,0)情况
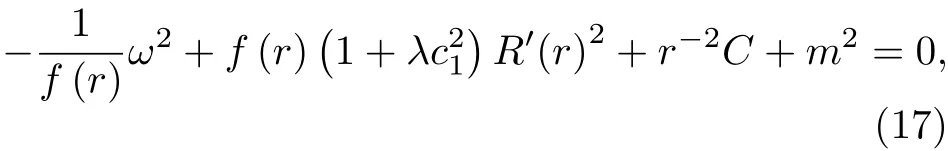
这里的C也是分离变量常数,因此有

黑洞的隧穿辐射率依然是(15)式的形式,但是其中霍金温度是

在这里修正后的霍金温度TH也与相关.
4 结 论
另一方面,黑洞热力学中另一个重要的物理量是黑洞的熵,修正的霍金温度也会带来黑洞熵的修正. 根据黑洞热力学有
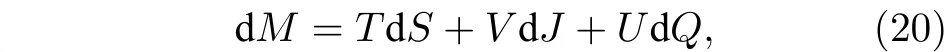
其中V和U分别是黑洞的旋转势和电磁势. 因此,在事件视界rh处未修正之前的黑洞熵满足
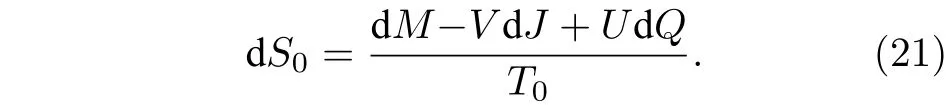
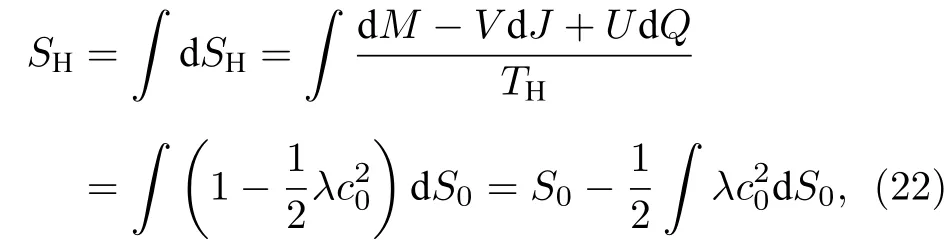
而在uα=的情况中,黑洞熵为

所以如果λ是一个正数,uα=和uα=的情况将导致黑洞的熵减小.
本文研究的是最简单的修正标量场情况,近来越来越多的高能物理研究倾向于认为洛仑兹对称性在高能尺度下会产生破缺,人们已经陆续提出各种洛仑兹破缺的量子场方程. 这些研究可能为将来量子引力的研究提供有力的支持. 在弯曲时空中,黑洞表面简单而极端的性质可能成为将来验证洛仑兹破缺理论的有力工具. 我们将继续研究关于弯曲时空中洛仑兹破缺的量子场论.

