基于动态因子图缩减的SCMA多用户检测算法

郝树良，刘 海，范 彬，张新苹，姚 稳（重庆邮电大学，重庆400065）

1 概述

目前，4G移动通信建设方兴未艾，5G移动通信研究已全面开启［1］。与4G相比，5G需要提供更高的频谱效率，支持更多的终端接入。为应对这些需求，5G需要更先进的多址接入技术。稀疏码分多址接入（SCMA）［2］技术作为非正交多址接入技术的候选方案之一，展现出了优越的过载性能，为5G多址技术候选方案之一［3-4］。

SCMA是由低密度扩频码分（LDS——Low Density Spreading）［5-6］接入技术衍生而来。与 LDS 不同，SCMA编码器是由正交振幅调制（QAM）映射器和符号级扩频联合而成，可以直接将用户的数据比特映射为多维复域的码字。SCMA系统采用精细设计的星座图来获得更高的整形与编码增益，从而实现其系统性能增益要优于LDS系统。SCMA要想成为未来5G选用的空口技术，有2个关键技术需要解决，一个是性能优异的稀疏码本设计，另一个是高效的多用户检测技术［7］。对于SCMA的码本设计，文献［8］已经进行了次优多阶设计。本文重点讨论接收端的多用户检测技术。

在接收端，SCMA系统采用的是具有较低复杂度的消息传递算法（MPA）［9］进行多用户检测。但是，在迭代次数过多，用户量增大，以及系统对分集增益需求更高的场景下，MPA算法的复杂度会急剧增大。针对MPA算法复杂度较高的问题，文献［10］提出了一种基于对数域的MPA，该算法在原始MPA算法的基础上通过从指数域到对数域的转换降低了一定的复杂度。文献［11］基于部分边缘化，提出了一种改进的MPA多用户检测算法，该算法在牺牲一定误比特率（BER）性能的情况下，使得算法的复杂度得到降低。文献［12-13］提出的次优的MPA多用户检测算法，更有效地接近最大后验算法（MAP）的性能。以上对于MPA算法的研究主要集中在每次迭代中的算法优化，并且每个码字的判决都需要经过固定次数的迭代后才能进行。文献［14］利用了在不同时隙的码字收敛情况的不同，其需要的迭代次数也就不同，提出了一种基于避免冗余迭代的MPA检测算法，该算法通过屏蔽冗余的迭代降低检测复杂度。

本文提出了一种基于动态因子图缩减的MPA（DFGR-MPA——Dynamic Factor Graph Reduction-MPA）检测算法，该算法根据每个变量节点（VN——Variable Nodes）的码字概率的收敛率把VN分为已完成迭代VN和未完成迭代的VN。定义码字概率的收敛率为码字当前迭代概率和前一次迭代概率的差与前一次迭代概率的比值。已完成迭代的VN不再参与后续的迭代并从因子图中除去，未完成迭代的VN与其相关功能节点（FN——Function Nodes）重构成新的因子图并完成后续迭代。这样不仅避免了已完成迭代VN的冗余迭代，还降低了后续迭代检测的复杂度。理论分析与仿真结果表明，DFGR-MPA检测算法能够保证在一定BER性能前提下实现一定程度复杂度的降低。

2 系统模型

SCMA系统的调制器可以定义为log2(M)个比特到K维复数域码字的映射，其中M为码本的维度，K为码本中每个码字向量的长度。所有的码字向量都具有稀疏性，即每个码字有N(N＜K)个非零元素。图1为SCMA上行链路系统。该系统中，有J=6个用户的数据流叠加在K=4个载波上，然后通过无线信道传输到同一个基站上去，其负载率为150%（λ=J/K，通常情况下λ≥1）。

SCMA系统的接收端接收到所有用户的叠加信号，可以表示为：

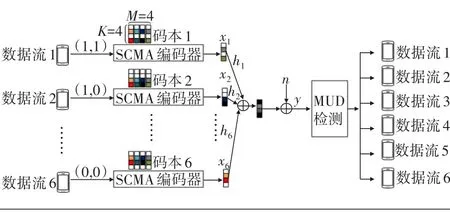
图1 J个用户、K个资源块的SCMA上行链路系统

式中：

y——接收机接收的所有用户的叠加信号，y=（y1，..，yK）T

xj——用户 j的数据比特映射的码字符号，xj=（x1，j，…，xK，j）T

hj——用户j的信道向量，hj=（h1，j，…，hK，j）T

n——均值为0，方差为σ2的高斯噪声向量，其中n=（n1，..，nK）T

第k个载波承载的接收信号yk可以用式（2）表示：

若该系统使用MAP算法需要遍历所有用户及其各自码字的组合，因此复杂度非常高，且随着用户的增长呈指数型增长，因此SCMA系统并不采用MAP算法。由于SCMA系统码本的稀疏特性，SCMA系统延续采用了LDS系统的MPA检测算法。相比于MAP算法，MPA具有较低的检测复杂度。

为了研究接收信号和每个用户之间的关系，可以用因子图矩阵F=(f1,...,fj)表示，其中 fj为用户节点（变量节点）j的二进制指示向量。当且仅当Fk,j=1时，变量节点vj与功能节点fk相连。本文中用到的因子矩阵如式（3）所示。根据SCMA的码本特点，多个用户传输的码字复用在同一资源块上，并且多个资源块上携带同一个用户的码字。因子图可以对用户与资源块之间的关系进行更好地表示，此外，因子图的引入为后续分析多用检测算法提供方便。图2为本文中用到的用户与资源块之间对应关系的因子图，该因子图对应的为文献［15］公开的四维码本。

图2 SCMA系统的因子图

3 多用户检测算法

3.1 原始MPA算法

3.1.1 原始MPA算法的详细过程

MPA算法的核心思想是通过FN与VN的消息传

步骤2：更新功能节点fk到变量节点vj传递的概率消息如式（4）所示。

步骤3：更新变量节点vj到功能节点fk的概率消息，如式（5）所示。

步骤4：当迭代次数达到预设的最大迭代次数Tmax后，每个用户码字的输出概率可以用式（6）表示：

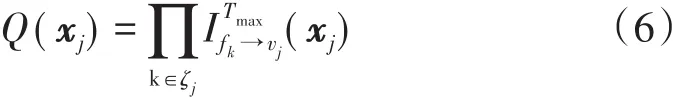
式（7）表示最后输出软判决信息，bxj,i=0表示变量节点vj第i个比特为0的码字；LLRi,j表示变量节点vj第i个比特的软判决输出，其中1≤i≤log2M。

3.1.2 原始MPA算法存在问题

在原始MPA算法中，虽然设置了最大迭代次数Tmax，但是不同的用户在不同时隙下需要的迭代次数并不相同。图3所示为在原始MPA算法下，6个用户在Eb/N0值为2 dB时的某个码字概率的收敛情况对比，其中最大迭代次数Tmax的值为8。从图3中可以看出，不同用户具有不同的截止收敛点。用户2在迭代次数t=2时已经完成收敛，则剩余的Tmax-t=6次迭代被称为冗余迭代；用户1、3、4、5在迭代次数t=3时已经完成了收敛，有5次冗余迭代；用户6在迭代次数t=4时完成收敛，有4次冗余迭代。冗余迭代的存在是MPA检测算法复杂度过高的原因之一。

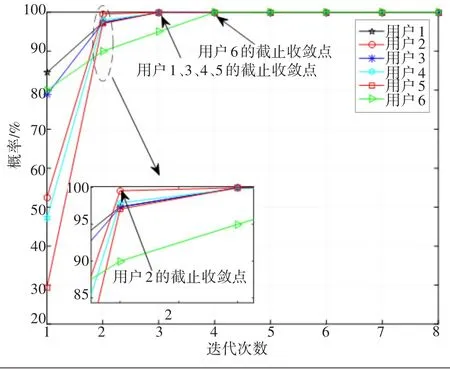
图3 MPA算法下6个用户的码字概率收敛对比

3.2 基于动态因子图缩减的MPA

3.2.1 DFGR-MPA算法理论分析

DFGR-MPA针对原始MPA存在的不同VN存在不同冗余迭代问题进行了改进。DFGR-MPA在每次迭代结束前需要根据每个VN的码字概率的收敛情况判断该节点是否进行后续迭代，若部分VN已经达到收敛则不再进行后续迭代，则剩余的VN需要继续完成相同的过程直到达到迭代停止条件为止。DFGRMPA中用户的码字概率是否收敛是根据其所有码字概率的收敛率wt(xj)为度量进行判定。若该值小于预先设定的阈值hD(0≤hD≤1)，则称该用户的码字概率已经达到目标收敛。收敛率wt(xj)的定义如式（8）所示。

该过程可以理解为每次迭代结束后，都要对此次迭代前的因子图进行缩减，剩余未达到目标收敛的VN和其相关联的边重构出一张只包括需要更新状态节点的因子图用来下次迭代。由于因子图都是根据每个用户节点的码字概率收敛情况进行动态地缩减，所以该算法被称为动态因子图缩减MPA算法。

DFGR-MPA在迭代过程中通过动态地缩减因子图的方法减少与迭代无关的FN和VN是一种降低复杂度的方式［13］。图4更加直观地表示了使用DFGRMPA算法迭代检测的复杂度降低。假设变量节点v1和v3在T1次迭代后已经完成概率的目标收敛，则v1和v3不再进行后续迭代，那么与变量节点v1和v3以及其相关联的边（图中用虚线表示）在因子图中缩减出去，不再参与迭代；用户v1和v3结束迭代后，功能节点f2的度由3降为1，f1和 f3的度有3降为2，这使得系统在T1+1次迭代时的复杂度大大降低。

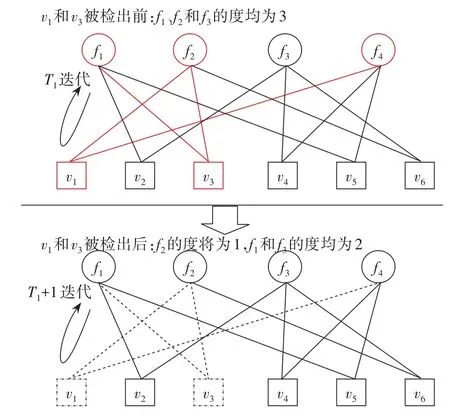
图4 DFGR-MPA算法的复杂度下降分析

基于动态因子图缩减的MPA多用检测算法具体过程如表1所示。其中Φt和Ψt为构成第t次迭代时因子图的FN和VN的集合。

3.2.2 复杂度分析

原始MPA算法需要计算出所有可能的信道系数与码字组合，即hk,mxk,m的值，该运算需要涉及到2MKdf次加法和4MKdf次乘法；在FN的消息更新时，MPA的每个节点需要(2df+1)Mdf-1次加法，(df+2)Mdf-1次乘法以及Mdf-1次指数运算；在VN进行消息更新时，MPA的每个节点需要(dv-2)次加法。DFGR-MPA与原始MPA算法复杂度的不同之处主要在VN更新的环节，因为该环节需要计算出每次迭代的收敛率，对于每个VN来说，每次迭代需要额外的2M乘法以及M次比较算法。DFGR-MPA在不同的迭代中，其参与迭代的FN和VN的数目不同。表2为MPA和DFGR-MPA的复杂度对比，其中ADD、MUL、EXP以及CMP分别表示加法运算、乘法运算、指数运算和比较运算，df和dv分别表示原始MPA算法中作用于功能节点的变量节点数和作用于变量节点的功能数，dfk,t和dvj,t分别表示DFGR-MPA算法中第t次迭代中作用于功能节点k的变量节点数和作用于变量节点j的功能节点数表示DFGR-MPA算法在当前时隙下迭代的最大次数。

表1 基于动态因子图缩减的MPA多用户检测算法

表2 MPA和DFGR-MPA的复杂度

4 仿真结果

为了验证本文所提出的基于动态因子图缩减的DFGR-MPA算法具有良好的系统性能，将其与次优的原始MPA算法进行比较仿真实验。在仿真中，各参数设置如表3所示，使用的码本为华为公司在文献［15］公开的4维码本。

表3 仿真参数

4.1 BER性能

图5显示的是本文算法DFGR-MPA与原始MPA算法的BER性能对比情况。从图5中可以看出，DFGR-MPA的阈值hD越大，其BER性能就越差；DFGRMPA的hD为0.01的BER性能与迭代次数Tmax为5的原始MPA算法性能几乎一致，在Eb/No的值为10 dB时，前者BER值为1.69×10-3，后者BER值为1.63×10-3，两者BER性能差值为5×10-5；阈值hD为0.6的DFGRMPA算法的BER性能与迭代次数Tmax为3的原始MPA算法性能相近。

4.2 复杂度对比

图6 为DFGR-MPA在不同Eb/No下的平均迭代次数。从图6中得出，3个不同阈值下的DFGR-MPA的平均迭代次数都要比迭代次数Tmax为5次的原始MPA要低。DFGR-MPA的最低迭代次数可以达到2.6次。这恰恰说明了DFGR-MPA能够通过降低迭代次数实现复杂度的降低。

在仿真过程中进行数据统计，并根据表2就能很容易得出DFGR-MPA与MPA的复杂度关系。为了更直观地比较2种算法复杂度的关系，采用复杂度降低比（CCRR）来度量，其定义为式（9）。在上文中已经提到，DFGR-MPA算法需要一定比较运算，由于该运算的复杂度较低，本文已将其忽略。图7为DFGR-MPA与原始MPA的CCRR曲线。从图7中可以看出，DFGR-MPA的CCRR值要比原始MPA高，其中阈值hD为0.60的DFGR-MPA最大CCRR值为58.5%，最低为23.0%。从图5中得知，阈值hD为0.60的DFGR-MPA算法的BER性能和迭代次数Tmax为3的原始MPA近乎相同，但前者相比后者有较高的CCRR，这恰恰证明了DFGR-MPA降低复杂度的有效性。

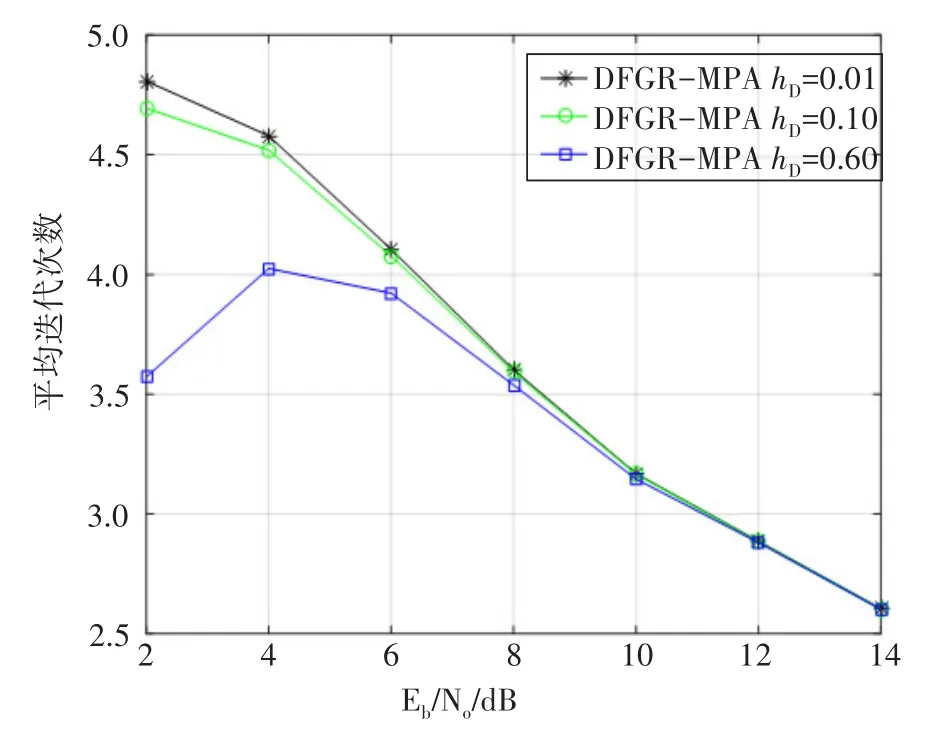
图6 DFGR-MPA在不同Eb/No下的平均迭代次数

图7 DFGR-MPA相对于与原始MPA的CCRR

5 结论

本文SCMA上行链路系统，以现有的MPA检测算法为基础，提出了一种动态因子图缩减的多用户检测算法，相比原始MPA，本文算法在算法复杂度明显降低的情况下，还能获得理想的BER性能。本文算法的思想不仅可以应用到原始MPA算法上，还可以应用到对数域MPA算法上，其复杂度的优势更佳。