复合式衬砌隧道总安全系数设计法修正与应用研究

肖明清， 徐 晨

(中铁第四勘察设计院集团有限公司， 湖北 武汉 430063)

0 引言

交通隧道常采用复合式衬砌。在复合式衬砌的初期支护计算方法方面，国内外众多学者进行了深入研究[1-3]，提出了工程类比法、特征曲线法、地层-结构法、基于极限分析的地层-结构法等方法，例如文献[4]介绍了锚杆的计算方法，但缺少明确的荷载值与安全系数计算； 在二次衬砌计算方面，一般采用荷载-结构法。由于初期支护和二次衬砌采用的计算方法不同，难以统一评价复合式衬砌这一整体结构的安全性。为此，肖明清等建立了复合式衬砌隧道总安全系数设计法[5-6]，并采用该方法分析了铁路隧道的安全性[7-8]，对锚杆作用、隧道承载主体、支护参数优化等争议问题进行了研究[9]。

总安全系数设计法的核心内容包括： 1)提出了采用围岩压力表征值来解决实际施工中围岩压力不确定问题的思路，并提出了围岩压力表征值的计算方法，得出了该计算方法具有安全性与经济性的结论[7，10]； 2)建立了喷层(为便于表述，不管喷射混凝土内是否含有钢筋网或钢架，均简称为喷层)、锚杆、喷层-锚杆-围岩组合承载拱3个荷载结构计算模型，用于初期支护的承载能力与安全系数计算[6]； 3)提出了复合式衬砌的总安全系数计算方法，并采用喷层-二次衬砌复合结构承载力计算模型对总安全系数计算方法的合理性进行了分析[9]； 4)提出了总安全系数的取值建议[5-9]。

在以往总安全系数设计法中，喷层、二次衬砌分别按现行隧道设计规范[11-12]采用破损阶段法进行截面强度校核； 对于喷层-锚杆-围岩组合承载拱，由于其为不同材料组成的结构，因此采用应力等效的方法将整个截面等效为T型截面。但由于目前规范中尚没有偏心受压状态下T型截面对应破损阶段的安全系数计算方法，因此采取了折中方法进行处理(即取围岩或喷层极限强度与不同材料截面边沿应力的比值作为安全系数，且极限强度考虑设计支护力的影响)，这就导致了承载拱安全系数计算方法与喷层、二次衬砌不一致，造成整个方法体系有不合理之处。此外，锚杆采用直接承受围岩压力的计算模型对于软弱围岩也有不合理之处(锚杆直接承受围岩压力主要用于悬吊杆模型，在软弱围岩中不适用)。因此，本文对上述不合理之处进行修正，然后采用修正后的设计方法再次分析高速铁路双线隧道和20世纪普速铁路单线隧道的安全性，并与挪威Q法支护参数进行对比，同时结合单线铁路隧道案例说明该方法的应用。

1 修正后的总安全系数设计法

1.1 围岩压力表征值的计算

1.1.1 采用围岩压力表征值作为设计荷载的必要性

施工完成后的一定时间内，围岩压力在某个具体位置为定值并作为恒载处理，但由于地质条件的千变万化、施工水平的差别、支护参数的不同，即使围岩条件相同，围岩压力在时空上也具有变异性，具有活载的特性。采用安全系数设计法时，荷载及组合应采用最不利工况，因此需要寻找围岩压力的最不利情况。为此，可以引入围岩压力表征值作为支护结构的设计荷载，来解决真实荷载难以确定的问题。需要说明的是，围岩压力表征值不是作用于支护上的实际值，只是一个用于结构计算的荷载名义值。显然，围岩压力表征值应具备安全性与经济性2个特征，即： 既要能够包络可能的最大围岩压力，又不能过于保守而影响经济性。

1.1.2 建议采用的深埋隧道围岩压力表征值计算方法

1.1.2.1 当埋深(H)不小于10～15倍洞径(D)时

当H≥(10～15)D时，对于符合摩尔-库仑强度准则的围岩，围岩压力表征值的计算公式如下。

竖向均布荷载：q=αγ(Rpd-a)。

(1)

水平均布荷载：e=βλq。

(2)

(3)

式(1)—(3)中：α、β分别为拱部和侧部围岩压力调整系数，一般不小于1.2，同时根据围岩产状等因素进行调整(如水平岩层，α可取大于1.0的系数，β可取小于1.0的系数)；γ为围岩重度；Rpd为pi=0时，θ=45°位置处隧道塑性区半径，pi为支护力，θ为塑性区半径取值位置与隧道横轴的夹角；a为当量圆圆心至45°位置处隧道开挖边界的距离；λ为围岩侧压力系数；R0为隧道开挖半径，断面非圆形时取当量圆半径；p0为围岩初始应力，自重应力场为主时，p0=γH；c为围岩黏聚力；φ为围岩内摩擦角。

式(3)为鲁宾涅特方程[2]，式(4)为著名的卡斯特纳方程[2]。当λ=1.0时，式(3)的计算结果与式(4)相同； 当λ≠1.0时，式(3)在θ=45°位置处隧道塑性区半径也与式(4)计算结果相同，但式(3)中的p0应取水平应力与竖直应力的平均值。

(4)

1.1.2.2 当埋深小于10～15倍洞径时

当H<(10～15)D时，按上述公式得到的结果误差较大，建议采用实际埋深下的弹塑性有限元方法求解无支护时的塑性区范围，并取拱部90°范围内的平均塑性区高度作为围岩压力表征值的等效高度。为保证安全，也可直接采用H=(10～15)D时的公式计算值。

1.1.2.3 深埋短区段软弱围岩的压力修正

当较差围岩的两端为较好围岩时，受空间效应的影响，实际围岩压力表征值要低于公式计算值，具体折减值与埋深、隧道洞径、较差围岩长度等因素有关。当Ⅴ级围岩两侧为Ⅳ级围岩，且围岩分界面与隧道轴线垂直时，采用三维有限元模型得出的400 m埋深Ⅴ级围岩压力表征值(无支护开挖，取Ⅴ级围岩中间位置拱顶90°范围内的平均塑性区高度作为Ⅴ级围岩压力表征值的等效高度)与式(3)计算值的比值ξ见图1[10]。

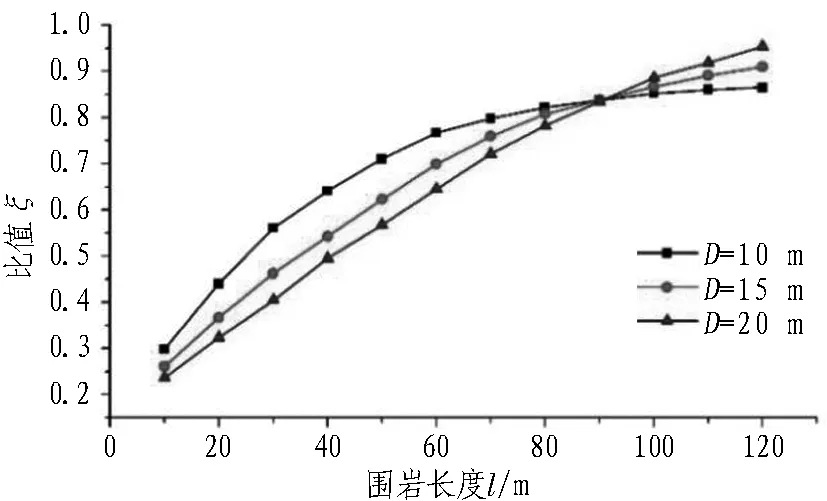
图1 Ⅴ级围岩长度、洞径对围岩压力表征值的影响

Fig. 1 Influence of length of grade V surrounding rock and tunnel diameter on representative value of surrounding rock pressure

由图1可知： 当围岩长度l较小时，其围岩压力表征值可以大幅度折减。此外，如果软弱围岩采取了超前注浆，则加固圈具有明显的承载作用，也可以显著降低围岩压力表征值。经计算，当隧道洞径为15 m、Ⅴ级围岩的加固圈厚度为3 m、加固体强度为2 MPa时，围岩压力表征值可减少70%～75%。

1.2 复合式衬砌的荷载结构模型

复合式衬砌一般由喷锚支护、二次衬砌以及中间的防水层组成，相应的在总安全系数设计法中，有喷层的计算模型(模型1)、锚杆-围岩承载拱计算模型(模型2)、锚杆的计算模型(模型3)、二次衬砌的计算模型(模型4)4个模型。其中，模型1、2、4的荷载均取围岩压力代表值。

1.2.1 初期支护方案

初期支护一般有以下3种方案。

支护方案1： 无系统锚杆支护结构，即初期支护主要由喷层组成，不设置系统锚杆，仅设置局部锚杆防止施工期掉块。

支护方案2： 喷锚组合支护结构，即初期支护由喷层和系统锚杆共同组成。

支护方案3： 以锚为主的支护结构，即围岩压力全部由系统锚杆-围岩承载拱承担，锚杆之间的局部松散荷载由薄的喷层承担。

1.2.2 模型1(喷层的荷载结构模型)

模型1中(见图2)，喷层采用梁单元模拟，结构与地层相互作用采用无拉径向弹簧和切向弹簧模拟。求得喷层的内力后，结构安全系数K1按现行隧道设计规范[11-12]采用破损阶段法进行计算； 当喷层内设置了钢架、钢筋网时，可按钢筋混凝土或型钢-混凝土组合结构计算。喷层作为结构层的最小厚度不宜小于8 cm[3]。

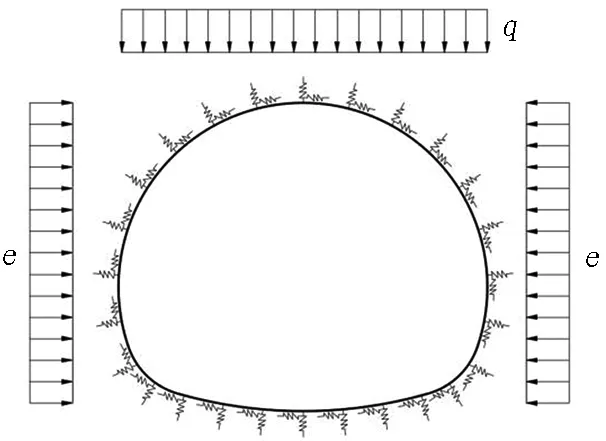
图2 模型1(喷层的荷载结构模型)

1.2.3 模型2(锚杆-围岩承载拱计算模型)

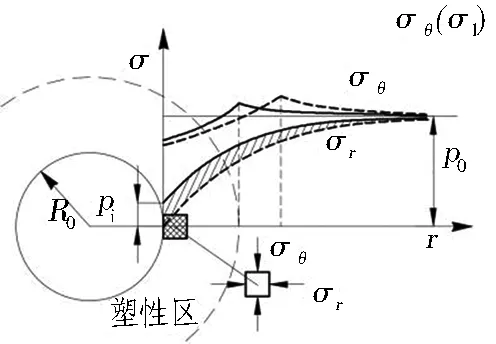
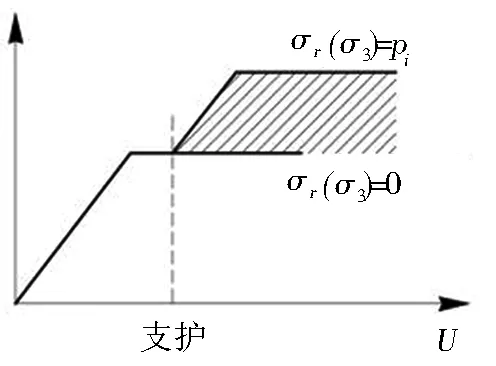
隧道开挖后，周边一定深度范围内的围岩进入塑性状态，无法承担后续增加的荷载，如图3所示。当采取喷层、锚杆等措施进行支护后，可增加塑性区围岩的侧限，进而增加围岩继续承载的能力。按此机制，可得出锚杆-围岩承载拱的计算模型见图4。

(a) (b)

σr为径向力，σθ为切向力，σ1为最大主应力，σ3为支护为围岩提供的支护力。

图3塑性区围岩在支护力作用下的承载机制

Fig. 3 Bearing mechanism of surrounding rock in plastic zone under supporting force

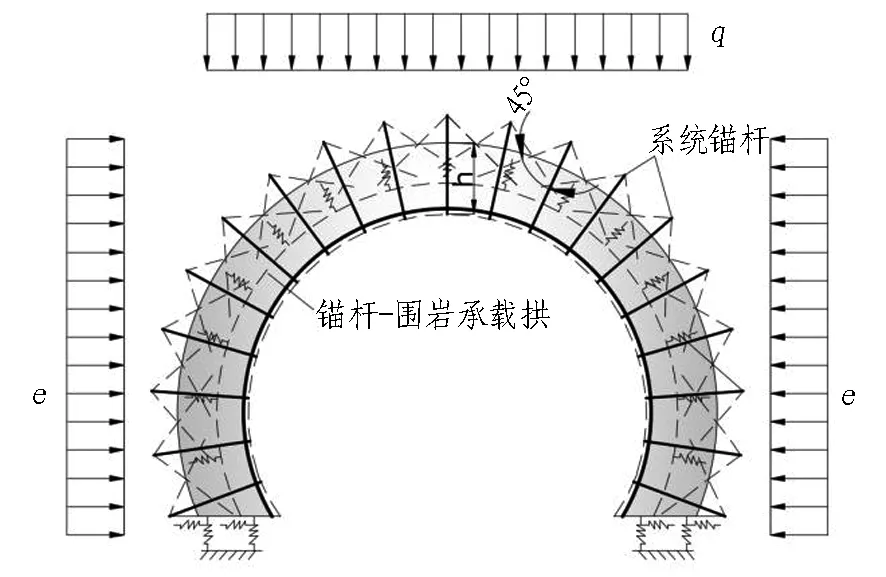
图4 模型2(锚杆-围岩承载拱的荷载结构模型)

Fig. 4 Model 2 (load-structure model of bolt-surrounding rock bearing arch)

模型2中(见图4)，锚杆的外端头按一定角度(如45°)向隧道内侧进行压力扩散，相邻锚杆压力扩散后的交点所形成的连线即为承载拱的外边线； 承载拱内边线为喷层外表面。承载拱采用梁单元模拟，采用径向弹簧模拟围岩与承载拱的相互作用，拱脚处采用弹性支撑，其余参数(如弹性模量、黏聚力、内摩擦角等)按勘察资料或现行规范选取。

求得承载拱的内力后，其安全系数K2按现行隧道设计规范采用破损阶段法进行计算。但承载拱范围内围岩的极限强度仅考虑支护后增加的强度，即： 将锚杆、喷层、二次衬砌提供的支护力作为σ3(计算详见1.2.4节)，进而根据摩尔-库仑强度准则得出围岩的σ1，此σ1即作为极限强度(当混凝土的极限应变小于σ1与围岩弹性模量之比时，应将二者的比值作为σ1的折减系数)。在施工期σ3由σ31(锚杆提供)、σ32(喷层提供)组成，施工期安全系数记为K2c； 在运营期σ3由σ31(锚杆提供)、σ32(喷层提供)和σ33(二次衬砌提供)组成，运营期安全系数记为K2op。

1.2.4 模型3(锚杆的计算模型)

锚杆的设计参数(长度、间距、直径)需结合模型2计算，并根据支护类型采用不同的方法。

1.2.4.1 采用喷锚组合支护时锚杆的计算模型

采用喷锚组合支护时，锚杆主要为模型2的承载拱提供部分侧限力(即σ3的一部分，σ3的另一部分由喷层、二次衬砌提供)，锚杆长度根据承载拱受力要求确定，锚杆的间距与直径(强度)根据需要其提供的侧限力进行计算(如图5所示)，且杆体本身的屈服强度安全系数不宜小于2.0，抗拔安全系数不宜小于2.5。

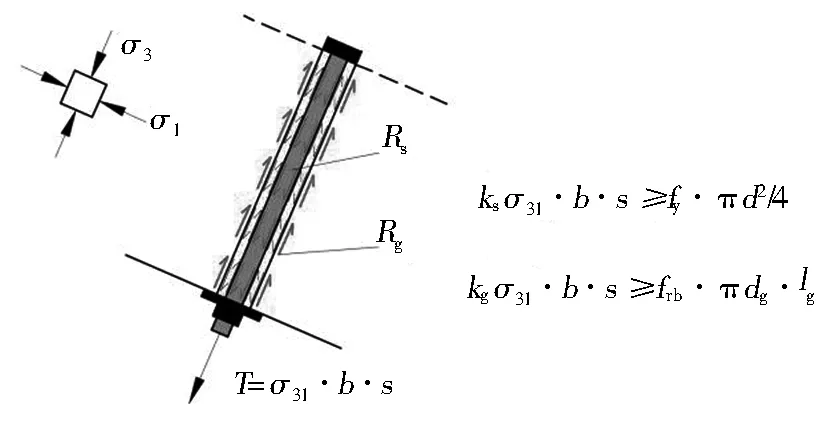
Rs为锚杆钢筋的承载力；Rg为孔道灌浆料(砂浆锚固体)与岩体之间的黏结力；T为锚杆轴力；ks为锚杆的屈服承载力安全系数；kg为锚杆的抗拔安全系数；σ31为锚杆提供的侧限力；fy为锚筋钢材的屈服强度；d为锚筋直径；frb为砂浆锚固体与地层间的极限黏结强度；dg为砂浆锚固体的外径；lg为锚筋与砂浆的锚固长度；b、s分别为锚杆的环向间距和纵向间距。

图5模型3(锚杆的荷载结构模型)

Fig. 5 Model 3 (load-structure model of bolt)

需说明的是，σ3由σ31(锚杆提供)、σ32(喷层提供)、σ33(二次衬砌提供)组成，施工阶段可不计入σ33，σ32和σ33可近似按以下公式计算。

σ32=0.5K1·q；

(5)

σ33=0.5K3·q。

(6)

式(5)—(6)中K1、K3分别为喷层、二次衬砌的安全系数。

1.2.4.2 采用以锚为主支护时锚杆的计算模型

当采用以锚为主的支护时，锚杆强度(屈服强度以及抗拔承载力)除满足承载拱受力所需的σ3要求外，还需满足最小支护力的要求。

文献[1]提出了最小支护力的估算方法： 当λ=1时，圆形隧洞围岩松动区内滑裂面为1对对数螺线，假设松动区内强度已大大下降，可认为滑移岩体已无自承作用以致于其全部质量由支护力pi，min来承担(如图6所示)，由此有：

(7)

式中Rmax为与pi，min相对应的松动区半径。

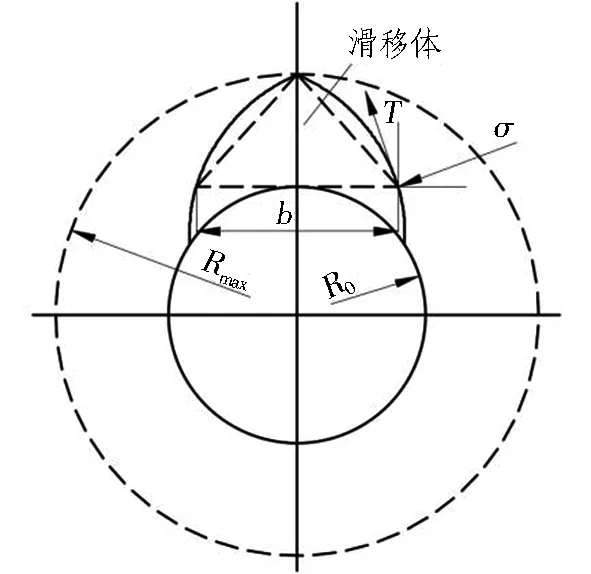
图6 最小支护力的计算图示

由切向应力σθ=P0确定松动半径Rmax：

(8)

由式(7)、式(8)联立可以解出最小支护力。

1.2.5 模型4(二次衬砌的计算模型)

二次衬砌的计算模型与模型1基本相同，但由于喷层与二次衬砌之间的防水层不传递剪力，故防水层设置区域二次衬砌与围岩的相互作用仅采用无拉径向弹簧模拟(见图7)，安全系数K3采用破损阶段法计算。

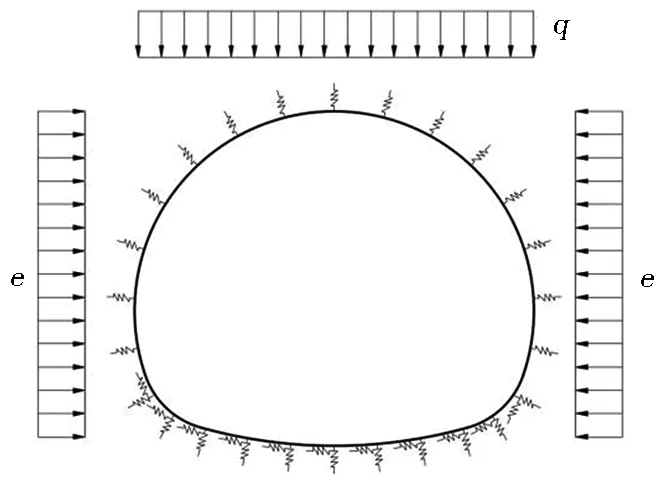
图7 模型4(二次衬砌的荷载结构模型)

1.2.6 不同支护方案计算模型的选择

1.2.1节所述3种初期支护方案可分别采用上述计算模型进行计算。

对于支护方案1，喷层的结构组成(喷混凝土、钢架、钢筋网等)、材料选择与尺寸参数等仅可采用模型1计算。

对于支护方案2，喷层可采用模型1计算； 锚杆的长度、间距、强度可采用模型2、模型3计算。此外，模型2中喷层提供σ32需要采用模型1的计算结果。

对于支护方案3，锚杆的长度、间距可采用模型2计算，锚杆材质、直径、抗拔所需长度可采用模型3计算。

对于二次衬砌，仅可采用模型4计算，但其强度对模型2的安全系数有影响。

1.3 复合式衬砌总安全系数计算方法与取值

1.3.1 复合式衬砌总安全系数计算方法

由上述初期支护方案及各计算模型可知，复合式衬砌的承载结构由2层(承载拱+二次衬砌、喷层+二次衬砌)或3层(承载拱+喷层+二次衬砌)组成。假设每层结构均为线弹性结构，且其中一个结构层的某一截面先达到极限强度时可以继续保持该强度，直至各层结构均达到极限强度时才出现完全破坏，则按上述方法分别计算喷层、锚杆-围岩承载拱、二次衬砌的安全系数后，复合式衬砌的总安全系数可以近似计算如下(K2在施工期和运营期分别采用K2c和K2op表示)。

施工阶段(无二次衬砌)：Kc=K1+K2c。

(9)

运营阶段，

采用耐久性锚杆：Kop=K1+K2op+K3。

(10)

采用非耐久性锚杆：Kop=K1+K3。

(11)

需说明的是，理论上在相同总安全系数的前提下可以有多种支护参数方案。由于不同支护方案中各层结构并非总是同时达到最不利截面强度，因此按公式(9)—(11)得到的总安全系数是整体结构的最小安全系数，实际承载能力一般会高于上述计算结果(详见1.3.3节)。同时，该计算方法也为整体结构的优化设计提供了一个目标函数，最为经济的结构应是实际承载能力接近总安全系数计算值，并根据造价、可实施性等因素进行选择。

1.3.2 总安全系数取值

建议运营阶段总安全系数Kop≥3.0～3.6，施工阶段(无二次衬砌)喷层、锚杆-围岩承载拱的总安全系数Kc≥1.8～2.1[5-6]。总安全系数可以根据结构重要性、围岩具体条件以及施工质量控制等因素进行调整。

1.3.3 喷层-二次衬砌复合结构的分析

锚杆-围岩承载拱位于整体结构的最外层，即使全部进入塑性状态，只要喷层与二次衬砌未出现整体失稳，则该结构不会单独失稳。因此，需要对喷层-二次衬砌复合结构的承载能力进行分析。

1.3.3.1 破坏阶段喷层-二次衬砌复合结构的承载能力分析模型

喷层与二次衬砌共同承载的复合结构计算模型如图8(a)所示，二者之间法向弹簧的刚度

(12)

式中：E1、E2分别为喷层、二次衬砌的弹性模量；h1、h2分别为喷层、二次衬砌的厚度；A为接触单元的面积。

当喷层或二次衬砌的某个截面达到破损阶段，假设其可以维持破损阶段的承载力，并将破损区域的内力作为边界条件施加在破损位置，再继续增大荷载直至结构整体破坏，其计算模型如图8(b)和图8(c)所示(分别对应大偏心受压破坏和小偏心受压破坏)。

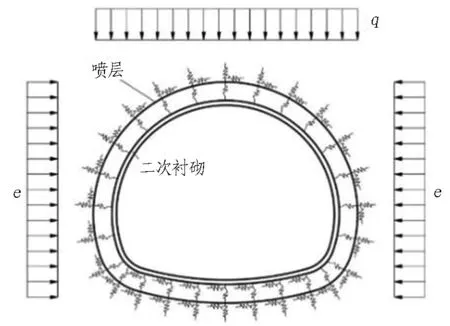
(a) 计算模型

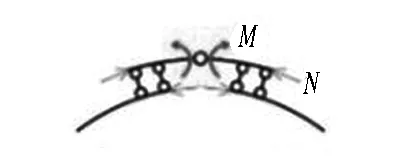
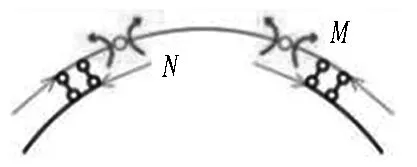
(b) 大偏心受压破坏 (c) 小偏心受压破坏

M为弯矩，N为轴力。

图8喷层-二次衬砌复合结构承载力计算模型

Fig. 8 Bearing capacity calculation model of shotcrete layer-secondary lining composite structure

1.3.3.2 复合结构破坏次序对承载力的影响

根据喷层与二次衬砌的破坏次序，复合结构(不含锚杆-围岩承载拱)整体破坏阶段的荷载比例系数Kd(即通过加大荷载值来使结构破坏的破坏荷载与设计荷载的比值，其内涵与安全系数不完全相同)与总安全系数法计算结果的对比可分为以下3种情况。

第1种： 当喷层与二次衬砌同时达到最不利截面强度，则Kd=K1+K3。

第2种： 当喷层先于二次衬砌达到设计强度，但由于二次衬砌位于其外侧，喷层不会整体失稳，可以继续承载，直至二次衬砌最不利截面达到破损阶段，此时Kd>K1+K3。

第3种： 二次衬砌先于喷层达到最不利截面强度，需要二次衬砌第一破损区继续发展或形成新的破损区时喷层才能达到破损阶段，此时Kd>K1+K3。

对于第3种情况，由于二次衬砌有多个破损区，虽然可以继续承载，但可能会超出正常使用对适用性的要求(如对于高铁隧道，拱墙部位的破损区可能因列车振动作用而发生掉块)，因此应通过断面形状的调整或喷层与二次衬砌强度的匹配来控制二次衬砌第一破损区的位置，使之不出现在拱墙部位； 对于第2种情况，也应合理控制喷层与二次衬砌的强度匹配，防止因喷层破坏区过大而使二次衬砌出现突然的脆性破坏。综上所述，合理的设计方案应是喷层与二次衬砌基本同时达到最不利截面强度，其荷载比例系数Kd基本等于或略高于K1+K3； 当高出K1+K3较多时，应调整设计参数或断面形状。

同理，也可建立锚杆-围岩承载拱、喷层、二次衬砌3层结构的整体承载力模型，但由于K2是基于喷层、锚杆、二次衬砌的破损阶段得出的，随着模型1、3、4达到破坏状态而达到最大值，因此3层结构实际上可以简化为图8所示的2层结构。同样，需要使荷载比例系数Kd基本等于或略高于K1+K2+K3。

2 既有隧道的安全性计算分析

以高速铁路双线隧道通用参考图和20世纪90年代编制的时速140 km单线电气化铁路隧道标准图为例，采用总安全系数设计法对其安全性进行计算分析。相关结构断面、支护参数与材料性能等分别见文献[5-8,13]。

2.1 时速350 km高速铁路双线隧道通用参考图的安全性分析

表1为所分析案例的安全系数计算结果(表中Ⅴ级围岩的荷载已考虑空间效应与注浆因素进行了折减，其取值为Ⅳ级围岩的1.8倍，下同)。由表1可知： 1)Ⅴ级特大埋深(800 m)的安全系数最接近最小安全系数要求(略高出最小安全系数3.0)，是最为经济的结构；其余情况的安全系数均偏高，具有一定的优化空间。2)施工期不考虑锚杆的作用时(对应实际施工中部分工点省略系统锚杆的情况)，除Ⅴ级特大埋深外，其余各种情况仅依靠喷层就可以提供足够的安全系数来保证围岩稳定，不仅间接说明了本计算与实际基本符合，也说明了支护参数具有优化的空间(即只要保证锚杆质量，就可以减少喷层强度)。

表1时速350 km高速铁路双线隧道安全系数

Table 1 Safety factors of 350 km/h high-speed double-track railway tunnel

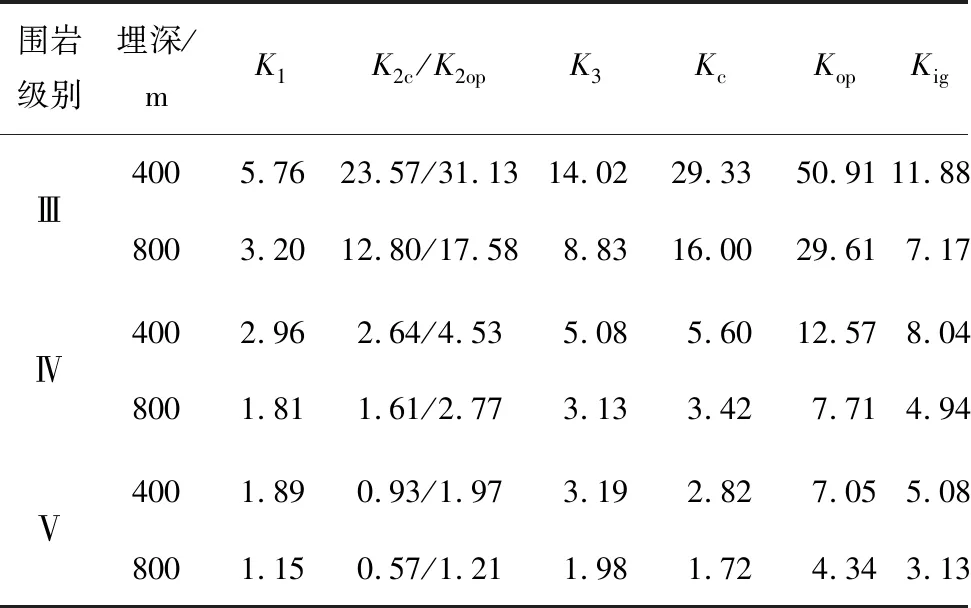
围岩级别埋深/mK1K2c/K2opK3KcKopKigⅢⅣⅤ4005.7623.57/31.1314.0229.3350.9111.888003.2012.80/17.588.8316.0029.617.174002.962.64/4.535.085.6012.578.048001.811.61/2.773.133.427.714.944001.890.93/1.973.192.827.055.088001.150.57/1.211.981.724.343.13

注：Kig表示忽略锚杆作用时的安全系数，下同。

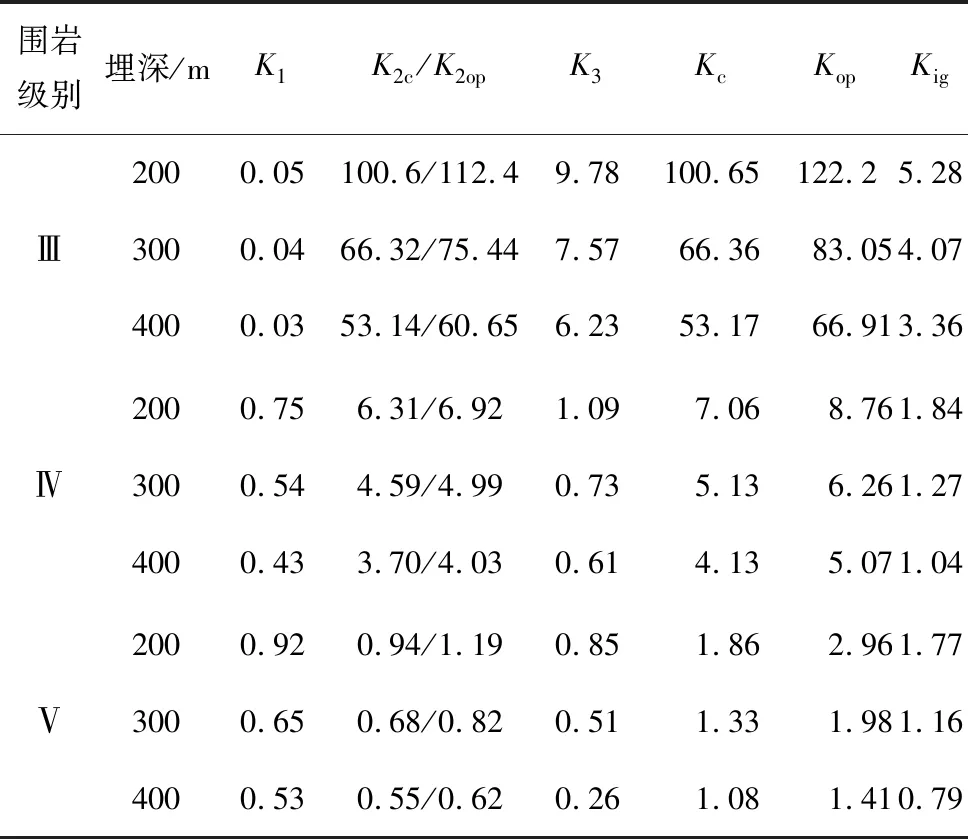
2.2 时速140 km单线电气化铁路隧道标准图的安全性分析

表2为所分析案例的安全系数计算结果。由表2知： 1)该支护参数在Ⅳ、Ⅴ级围岩地段的运营期总安全系数偏低(不考虑锚杆耐久性)，特别是锚杆-围岩承载拱所提供的安全系数在总安全系数中的占比较大，而所采用的锚杆并非耐久性锚杆，因此结构开裂的可能性随运营时间的延长会加大，需要特别关注(安全系数偏低，意味着失效概率增加)。文献[14]指出，既有铁路隧道病害问题日益突出，据统计，约有70%隧道存在渗漏水现象，且在2002年以前的运营铁路隧道中衬砌裂损病害较严重，可见本文计算结果与既有隧道病害较为普遍的现状基本相符。2)该标准图中说明了其适用埋深不宜大于300 m，由本文计算结果可知，当埋深达到400 m时，Ⅳ、Ⅴ级围岩地段的安全系数偏低，说明支护参数与埋深相对应的设计方法是合理的。

表2时速140 km单线电气化铁路隧道安全系数

Table 2 Safety factors of 140 km/h electric single-track railway tunnel

围岩级别埋深/mK1K2c/K2opK3KcKopKigⅢⅣⅤ2000.05100.6/112.49.78100.65122.25.283000.0466.32/75.447.5766.3683.054.074000.0353.14/60.656.2353.1766.913.362000.756.31/6.921.097.068.761.843000.544.59/4.990.735.136.261.274000.433.70/4.030.614.135.071.042000.920.94/1.190.851.862.961.773000.650.68/0.820.511.331.981.164000.530.55/0.620.261.081.410.79

3 与挪威Q法的支护参数对比

20世纪90年代，挪威学者Barton提出了著名的Q法[15]，在世界各地得到了广泛应用。一般认为，Q法支护参数是比较经济的，为分析其安全性并与总安全系数法相互验证，以时速350 km高速铁路双线隧道为例对Q法支护参数的安全性进行分析，并对采用与挪威同样的耐久性锚杆时高铁隧道复合式衬砌可能的一种优化支护参数进行计算。计算时，Ⅲ、Ⅳ、Ⅴ级围岩分别采用规范中物理力学指标范围值的下三分之一分位值。根据不同埋深，本文估算了所采用围岩参数对应的Q值，并根据文献[15]列出了相应的支护参数，相关计算结果见表3。

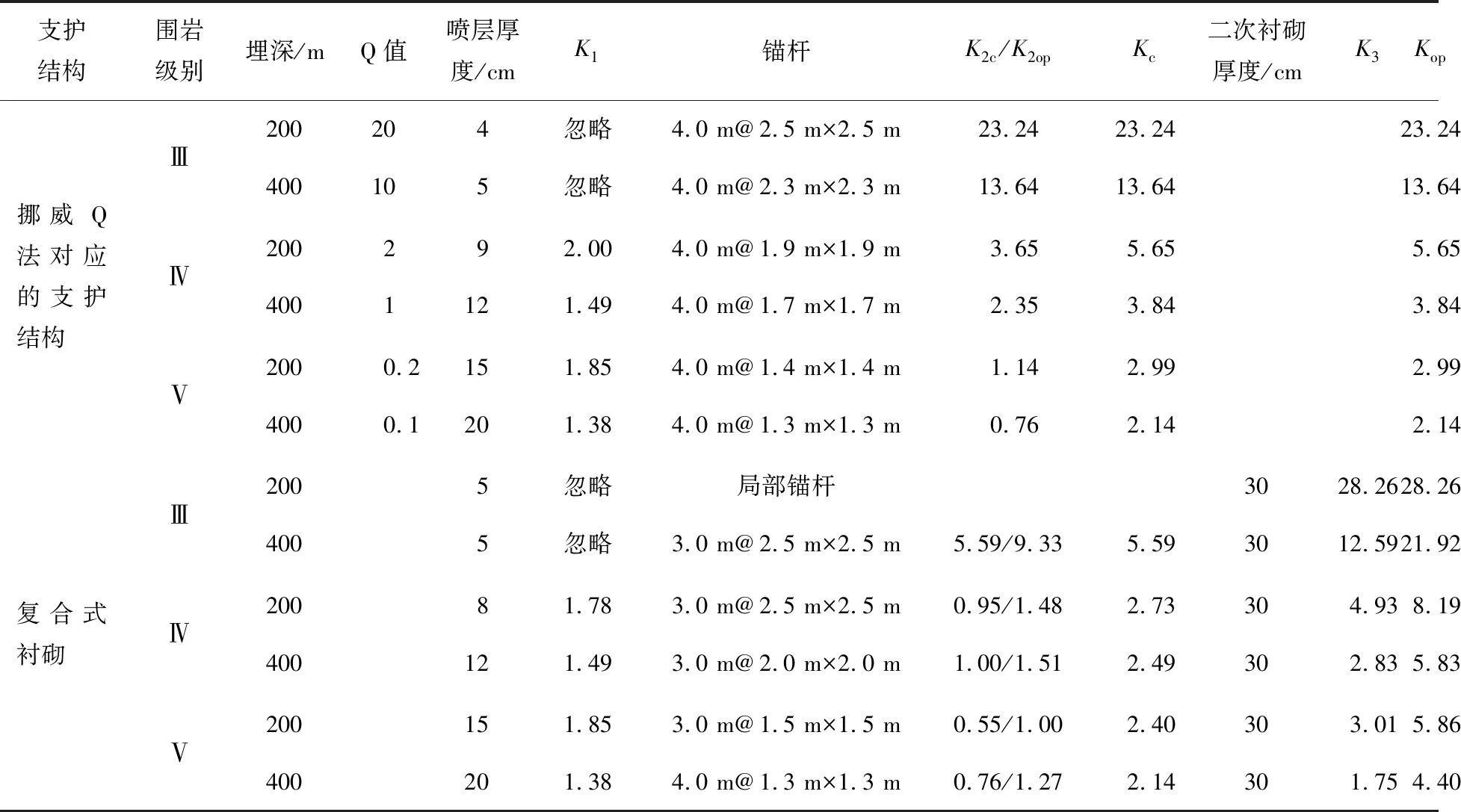
表3 支护参数与安全系数计算结果

注： 1)表中锚杆均采用M33-CT耐久性锚杆，承载力为345 kN； 2)本次计算喷层采用C30喷射混凝土，二次衬砌采用C30素混凝土； 3)Q法不设置二次衬砌，故K2c=K2op。

由表3可知： 1)Q法支护参数用于我国高铁双线隧道时，Ⅲ、Ⅳ级围岩总安全系数满足本文提出的建议值要求且较为经济，但Ⅴ级围岩安全系数偏低； 2)采用复合式衬砌时，如果二次衬砌采用30 cm C30素混凝土，则初期支护仅需满足施工期的安全系数要求，与Q法相比可以减弱锚杆参数； 3)采用耐久性锚杆有利于充分发挥锚杆-围岩承载拱的永久支护作用，与既有通用图支护参数相比，可以减少喷层和二次衬砌的强度，提高经济性。

4 总安全系数法在隧道断面形式比选中的应用

采用工程类比法设计时，无法得出不同断面形式对安全性的影响； Q法支护参数选择考虑的断面因素主要是隧道跨度或高度，也无法体现断面形式的差异。为了进一步说明总安全系数设计法的应用，以时速160 km单线铁路隧道为例来说明断面形式与支护参数的比选。

4.1 隧道断面形式与支护参数方案

对时速160 km单线铁路隧道拟定了2种断面形式(见图9)、3种支护参数方案，3种支护方案在Ⅴ级围岩条件下的支护参数见表4。方案1开挖宽度为8.34 m，高度为10.15 m，高跨比为1.22，如图9(a)所示； 方案2开挖高度与方案1相同，但开挖宽度增加1 m，高跨比变为1.09，如图9(b)所示。方案1、方案2采取相同的支护参数，方案3断面形式与方案2相同，但根据总安全系数法对支护参数进行了调整，拟定了400 m和800 m埋深的2种支护参数。

(a) 方案1 (b) 方案2

Fig. 9 Two cross-section forms of 160 km/h single-track railway tunnel (unit: cm)

4.2 安全系数计算结果

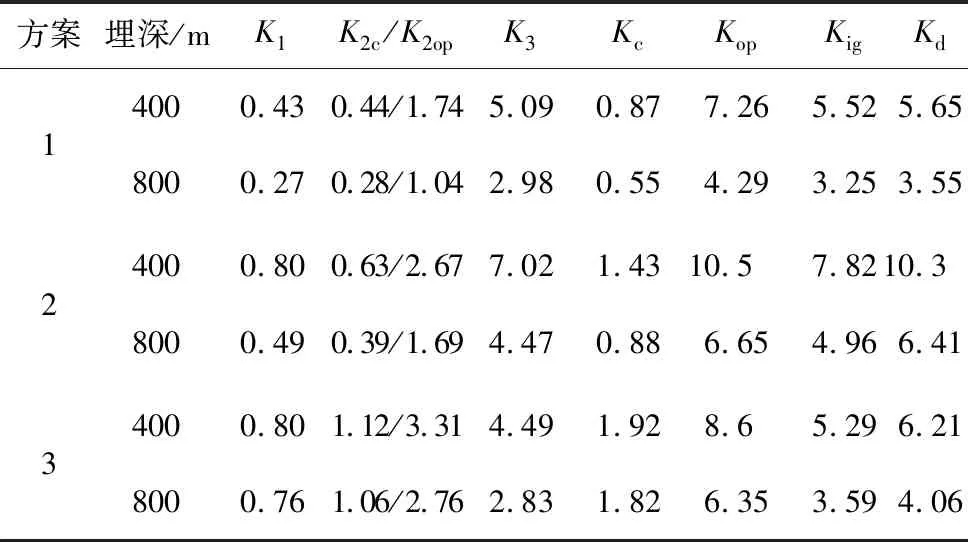
计算所得的安全系数如表5所示。由表5可知： 1)方案2与方案1相比，支护参数相同，但高跨比由1.22减少至1.09，支护的总安全系数大幅提高，说明断面形式对安全系数具有显著影响； 2)方案1与方案2的初期支护安全系数均偏低，无法满足施工期安全系数要求，需要及时施作二次衬砌； 3)方案3在方案2的基础上，根据埋深设置了不同的支护参数，在总安全系数满足要求的前提下，减小了二次衬砌的安全冗余并提高了初期支护的安全系数，具有更为合适的安全性与经济性。

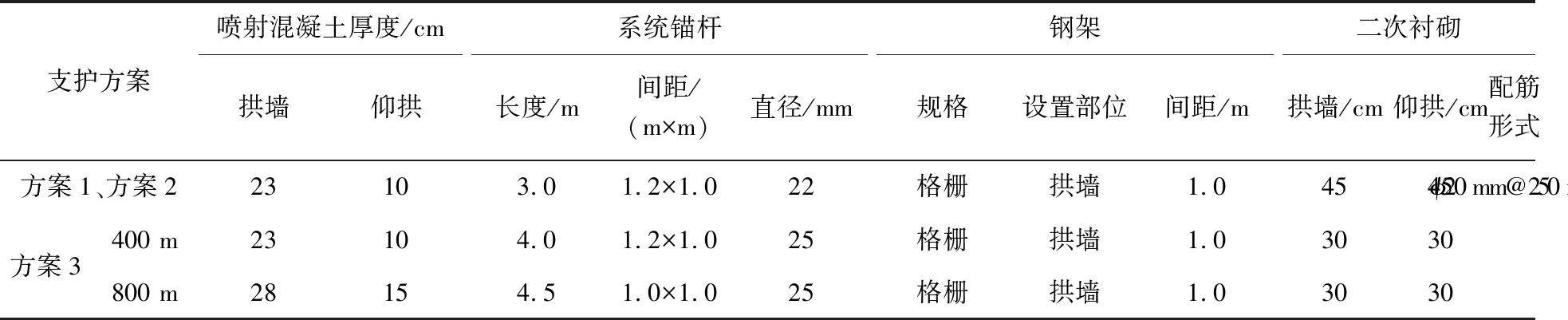
表4 时速160km单线铁路隧道支护参数

表5时速160 km单线铁路隧道3种方案安全系数

Table 5 Safety factors of 160 km/h single-track railway tunnel under three schemes

方案埋深/mK1K2c/K2opK3KcKopKigKd1234000.430.44/1.745.090.877.265.525.658000.270.28/1.042.980.554.293.253.554000.800.63/2.677.021.4310.57.8210.38000.490.39/1.694.470.886.654.966.414000.801.12/3.314.491.928.65.296.218000.761.06/2.762.831.826.353.594.06

4.3 喷层-二次衬砌复合结构的承载力分析

采用喷层-二次衬砌复合结构承载力模型分析表明，3种方案喷层均先于二次衬砌破坏，喷层为墙脚区域小偏心受压破坏。方案1的二次衬砌破坏位置位于墙脚区域，为大偏心受压； 方案2与方案3的二次衬砌破坏位置位于边墙，为小偏心受压，说明断面调整改善了结构的受力状态。

表5示出喷层-二次衬砌复合结构破坏阶段的荷载比例与喷层、二次衬砌的总安全系数对比结果，可以得出： 1)方案1和方案3(2种支护方案)复合结构整体破坏阶段的荷载比例系数Kd仅略高出K1+K3(分别高出2%～9%、17%、13%)，说明喷层与二次衬砌具有较好的强度匹配关系； 2)方案2总安全系数过高，且整体破坏阶段的荷载比例系数Kd比K1+K3高出较多(29%～32%)，说明初期支护与二次衬砌的匹配不合理，主要是二次衬砌过强，需要优化； 3)安全系数相加的方法为整体结构的优化设计提供了一个目标函数，并可通过喷层-二次衬砌复合结构承载力模型进行具体验证与优化。

5 结论与建议

1)提出了采用围岩压力表征值作为设计荷载的思路，可以解决设计中围岩压力不确定的问题。当H≥(10～15)D时，对于符合摩尔-库仑强度准则的围岩，可以采用式(1)—(3)计算围岩压力表征值；当H<(10～15)D时，为安全考虑，可以直接采用H=(10～15)D时的公式计算值。当较差围岩的两端为较好围岩时，围岩压力表征值需要考虑空间效应进行折减，具体折减值与埋深、隧道洞径、较差围岩段的长度等因素有关。此外，如果软弱围岩采取超前注浆，则加固圈具有明显的承载作用，也可以显著降低围岩压力代表值。

2)建立了复合式衬砌各支护层(喷层、锚杆-围岩承载拱、二次衬砌)的荷载结构模型与安全系数计算方法，提出了施工期、运营期总安全系数计算方法与取值，提出了喷层-二次衬砌双层结构以及承载拱-喷层-二次衬砌3层结构的破坏次序与总承载力分析模型，可用于各支护层的安全性校核、强度匹配与参数优化。所建立的总安全系数设计法能够体现锚杆-围岩承载拱、喷层、二次衬砌各自的承载作用与承载能力，为初期支护和复合式衬砌的支护构件选择、量化设计以及多层结构的整体优化设计提供了一定的理论基础。

3)对时速350 km高速铁路双线隧道通用参考图和20世纪90年代编制的时速140 km单线电气化铁路隧道标准图的安全系数计算结果表明，总安全系数设计法得出的结论与现场实际施工情况、既有隧道病害情况基本相符。

4)与挪威Q法支护参数的对比表明，Q法的支护参数如用于我国时速350 km高速铁路双线隧道，Ⅲ、Ⅳ级围岩满足本文提出的总安全系数建议值要求且较为经济，但Ⅴ级围岩安全系数偏低。当采用与Q法相同的耐久性锚杆时，所得出的高铁双线隧道支护参数与现行通用参考图有较大差别。采用耐久性锚杆有利于充分发挥锚杆-围岩承载拱的永久支护作用，从而可以减少喷层和二次衬砌的强度，提高经济性。

5)对时速160 km单线铁路隧道断面形式与支护参数的研究表明，总安全系数设计法可以用于隧道断面形式与支护参数的精细比选，克服了工程类比法和Q法等方法不能体现隧道断面形式差异的缺点。

需说明的是，本文所建立的总安全系数设计法尚缺少室内试验和现场验证的支撑，特别是锚杆-围岩承载拱的承载能力与安全系数计算方法需要进一步的试验研究。此外，如果喷层-锚杆-围岩作为一个整体结构(等效T型截面)进行计算，相比本文应该更为合理，但目前规范中尚没有偏心受压状态下T型截面对应破损阶段的安全系数计算方法，还有待进一步试验研究。