天然气水合物试采中节流螺旋管段微米级砂粒运移沉积规律数值模拟

苏义脑 陈 烨 孙晓峰 闫 铁 曲晶瑀 段瑞溪

1.东北石油大学石油工程学院 2.中国石油海洋工程有限公司

0 引言

我国海域天然气水合物（以下简称水合物）资源丰富，其储层特点与日本类似，储层埋深浅，胶结较弱，未固结成岩，水合物在砂土中以填充、骨架和胶结几种土体赋存方式存在[1-5]，一旦试采破坏了水合物的赋存条件[6-7]，起胶结和骨架支撑作用的水合物土体就会失去支撑，储层砂粒在地层流体的携带下流向井筒。水合物储层岩性以微米级黏土、粉砂、细砂为主，南海多个站位岩心样品粒度分布测试结果显示粒径小于63 μm的粉砂超过65%[8-10]，有的站位超过70%[11]，甚至有测试结果显示小于63 μm的黏土和粉砂占比接近94%[12]。对于微米级的泥质粉砂，防砂技术难度较大，目前水合物试采所用的防砂技术主要包括机械防砂、加装防砂网、射孔砂筛防砂、Geoform防砂系统等，这些防砂技术效果并不理想，实践和研究表明，防砂系统很难对粒径44 μm以下的砂粒发挥作用[13]。近年来，陆地（加拿大，2007年）和海域（日本，2013年、2017年）水合物开采，都发生了因微米级砂粒突破防砂设施进入井筒，引起井筒砂埋、堵塞，迫使水合物试采作业提前终止的案例[14-16]。日本共进行了两次大规模海域水合物开采试验，其中2013年为世界首次海域水合物开采试验，共产气6天，日产气2×104m3，后由于大量储层砂粒突破防砂设施进入井筒，导致试采提前结束[15,17-19]。2017年，日本总结第一次水合物试采经验，进行第二次海域水合物试采作业，同样由于井筒沉砂堵塞而终止产气[20]。因而，水合物开采过程中不仅需要考虑储层微米级砂粒突破井筒防砂设施后井筒设备的磨损问题，更要考虑微米级砂粒在井筒内的运移、沉积、堵塞问题，需要对微米级砂粒进入井筒后的运移沉积规律特征进行研究。

目前，水合物出砂研究主要集中在地质储层中，包括储层岩石力学特性（产砂机理）[21-27]、驱动力[28]、出砂风险[29-33]、评价防砂方法有效性[34-37]几个方面，而微米级砂粒随地层流体进入井筒后的运移、沉积、堵塞研究尚未见文献报道。本文研究的目的是：①通过数值模拟，获得微米级砂粒在节流管线螺旋段的运移沉积特征；②获得粒径、水速等参数对微米级砂粒运移沉降的影响规律；③获得不同情况下的砂粒临界不沉积水速，建立局部复杂井段微米级砂粒运移沉积预测模型，为水合物开采井筒砂埋提供预测方法；④为减小砂堵风险、确定合理开采工作制度、保证井筒安全提供依据，为后续水合物储层适度防砂工艺的发展提供技术支撑。

1 计算方法

1.1 计算模型

降压开采法是目前水合物开采的主流方法之一。前苏联麦索亚哈、加拿大麦肯齐、美国阿拉斯加北坡、日本南海海槽东部、日本南海海槽、中国南海神狐都采用过降压法开采水合物[20]，日本2013年在南海海槽东部采用降压开采法进行了第一次海域水合物试采作业，其开采系统如图1-a所示。

降压破坏了水合物稳定赋存的压力条件，使水合物发生分解，产生甲烷气和水，分解后产生的气液两相在井下分离并通过独立的管路产出，其中的甲烷等烃类气体通过油管通道举升到地面，分离水通过节流管线单独输运到井口。分离水在井下分离后经过C型通道进入节流管线，由于节流管线下部为刚性管路，且上下接箍位置不在同一侧，因而存在一段螺旋段，如图1-b所示。可见，水流通道既存在C型段，也存在螺旋段，是流道复杂砂粒易沉降的位置。为此，对水合物开采局部复杂管路微米级砂粒运移规律进行数值模拟研究，建立计算的几何模型如图1-c所示。由于节流管线为水流通道，为此选定水为连续相，微米级砂粒为分散相。

1.2 控制方程

连续性方程为：

式中下标l和s分别表示水和微米级砂粒；α表示浓度；表示速度向量；ρ表示密度。

每个计算单元相互渗透，因此他们浓度的和是一致的。水和砂粒的动量方程可以表示为：

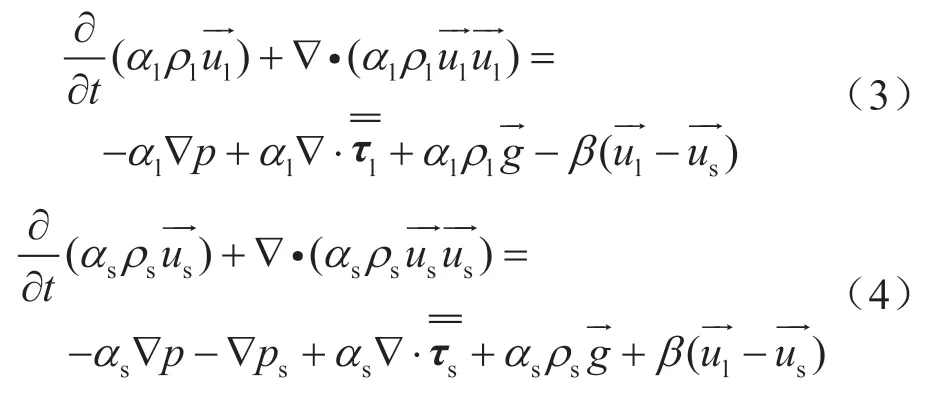
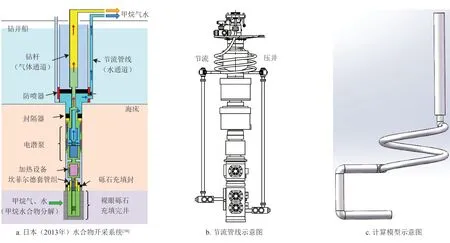
图1 水合物开采系统、节流管线及计算模型示意图

当αl≤0.8时，水—砂粒的交换系数可以表示为：

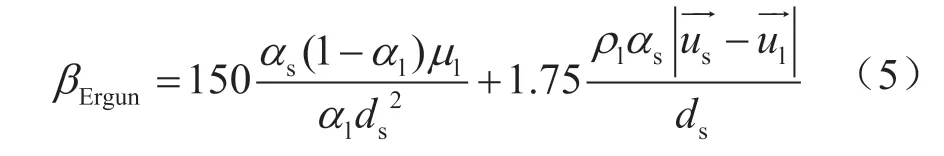
当αl＞0.8时，水—砂粒的交换系数可以表示为：

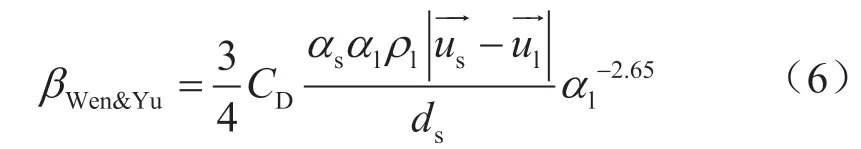
拖拽系数（CD）可表示为：

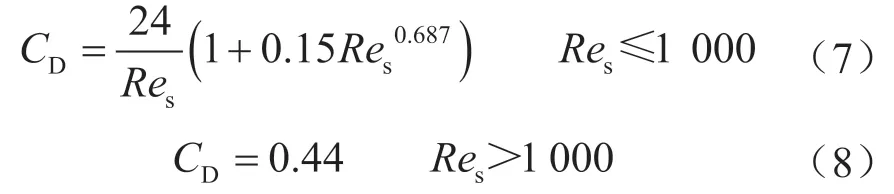
砂粒的雷诺数定义为：

式中ds表示砂粒粒径。

各相的应力—应变张量可表示为：

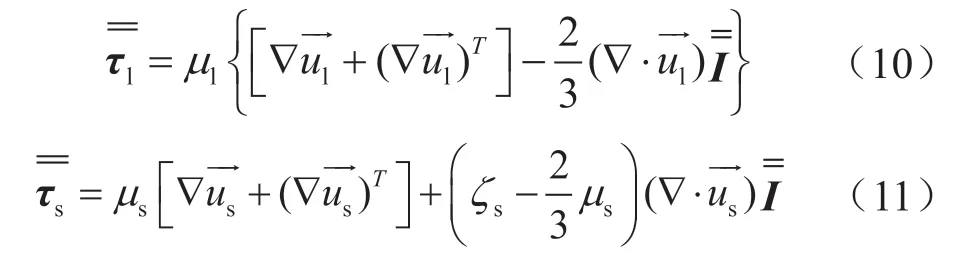
Realizablek—ε模型中的湍动能（k），耗散率（ε）为：

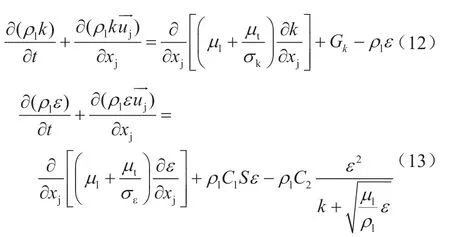
式中σk和σɛ分别表示湍动能方程k和耗散率方程ε的紊流普朗特数；C2表示常数。

Gk表示由于层流速度梯度而产生的湍流动能，可以表示如下：

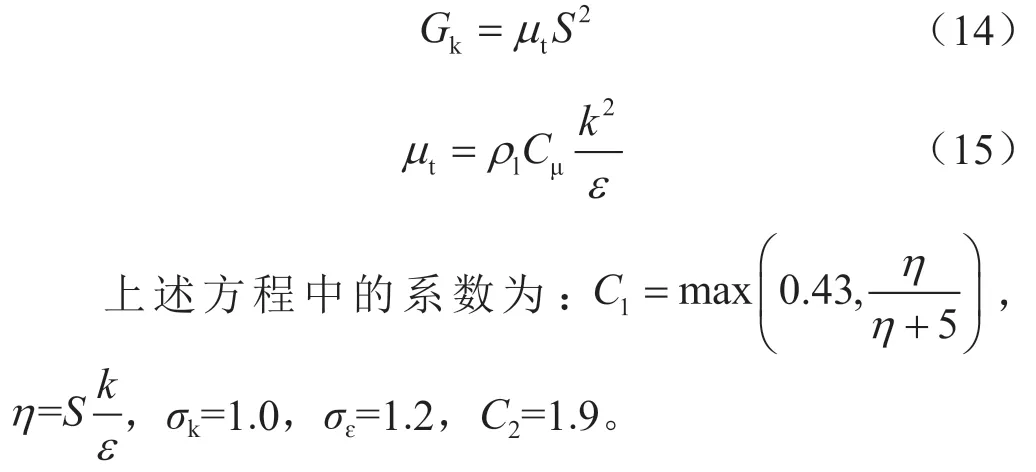
1.3 边界条件及网格划分

水和均匀分散的微米级砂粒从节流管线底部进入，经C型段、螺旋段后进入垂直段而后到达地面，如图2所示。在入口处选择速度入口边界条件，出口选择压力出口边界条件，壁面采用无滑移壁面条件。

适当的网格划分软件和高精度网格质量是CFD计算的必要先决条件。为提高计算准确性，加快计算和收敛速度，使用ICEM软件采用“自下而上”方式对计算流场划分六面体结构网格，图2为整体计算流场及局部位置三维网格划分示意图。设置边界层网格，管路径向第一层网格高度的选取符合y＋≈30，网格增长率取1.2，沿径向第一层网格高度采用式（16）计算

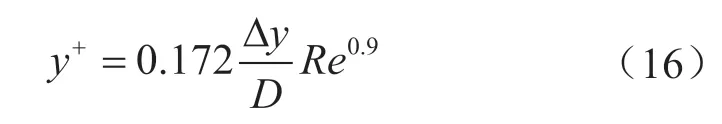
式中Δy表示第一层网格高度，mm；Re表示雷诺数；D表示水力特征长度，mm。

为了检测网格独立性，划分3种数量网格（158 347，200 816，411 075）用于流场（44 μm，1%浓度）模拟，模拟结果如表1所示。可以看出其相对误差均小于4.5%。综合考虑计算资源消耗、计算准确性，选择网格数200816进行数值模拟计算。

通过有限体积法对控制方程进行离散化之后，将相位耦合的SIMPLE算法应用于压力—速度耦合。动量方程使用二阶迎风格式进行离散化以提高计算精度。对每个尺度残差分量采用10－5的收敛准则来确定两个连续迭代之间的相对误差。时间步长取0.005 s，每个步长迭代20步。

选取3种粒径砂粒（44 μm，10 μm，4 μm），3种出砂浓度（1%，5%，10%），多种流速进行数值模拟计算，获得不同流速下微米级砂粒在复杂井段的运移沉积情况，以进一步确定不同粒径砂粒在不同浓度下运移的临界不沉积水速。

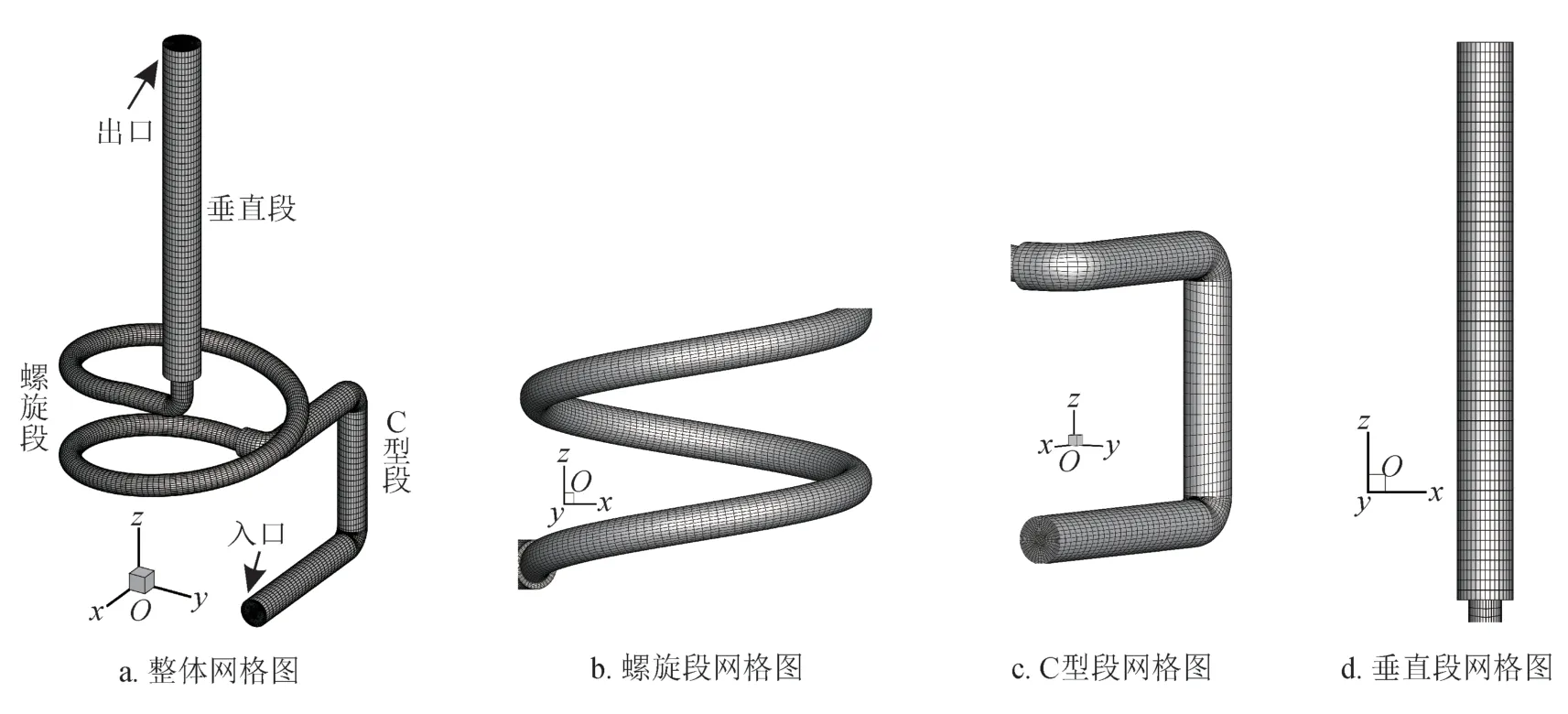
图2 整体计算区域及局部位置3D网格划分图

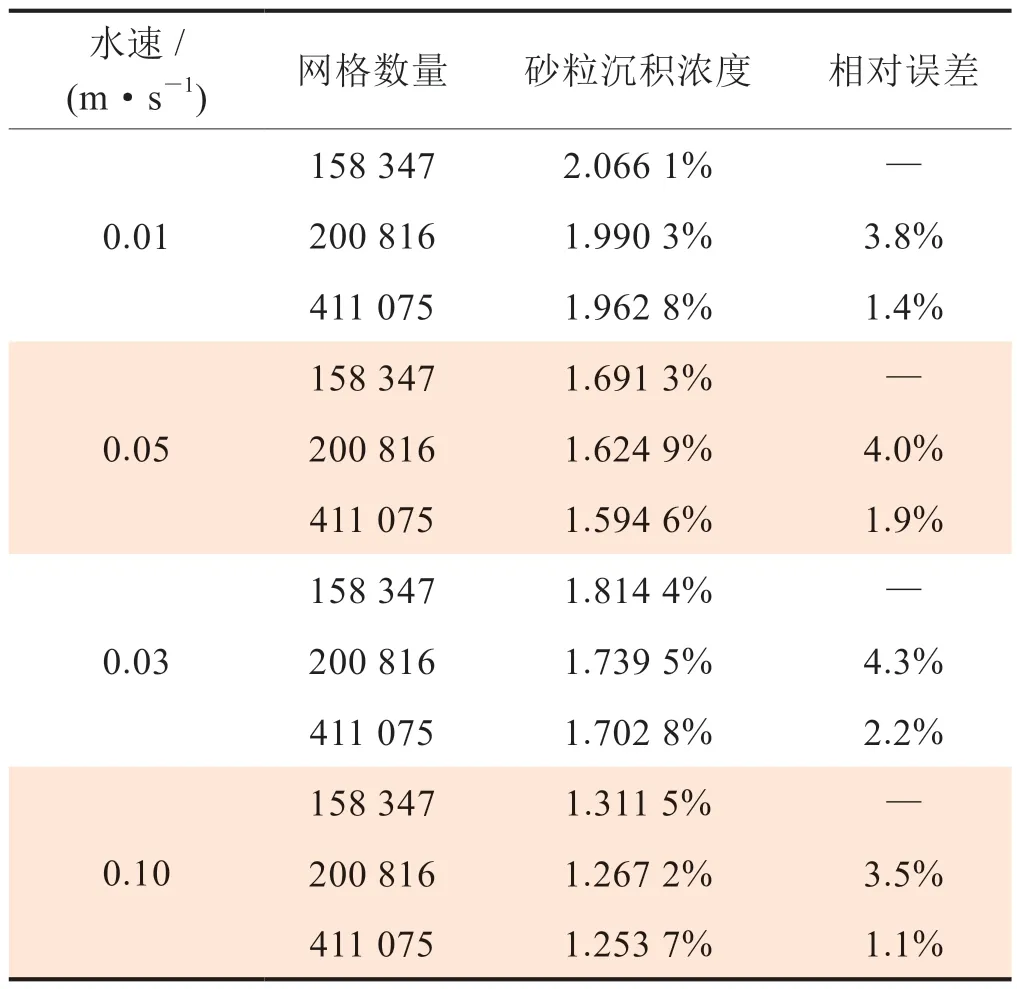
表1 网格独立性检验表

2 模拟结果及分析

2.1 微米级砂粒沉积分析

图3显示了44 μm粒径、10%出砂浓度在不同水速下微米级砂粒浓度分布云图。

由图3可以看出水速较小时，微米级砂粒在管路中的沉积较为明显，主要集中在C型段和螺旋段的下部（图3-a）；局部砂粒浓度最高达0.55。随着流速的增加，砂粒沉积情况改善较大，C型段、螺旋段下部沉积减少，局部砂粒浓度最大为0.24，集中在螺旋段中上部，管路其余部分多为0.12左右（图3-b），继续增大水速，微米级砂粒沉积越来越小，只在C型段转角留存有部分沉积（图3-c）。可见，微米级砂粒对水速较为敏感，较小的水速变化就能引起较大的砂粒浓度的变化。微米级砂粒较易沉积的部位主要在C型段的拐角处及螺旋段，这是由于流向变化和重力作用引起的。

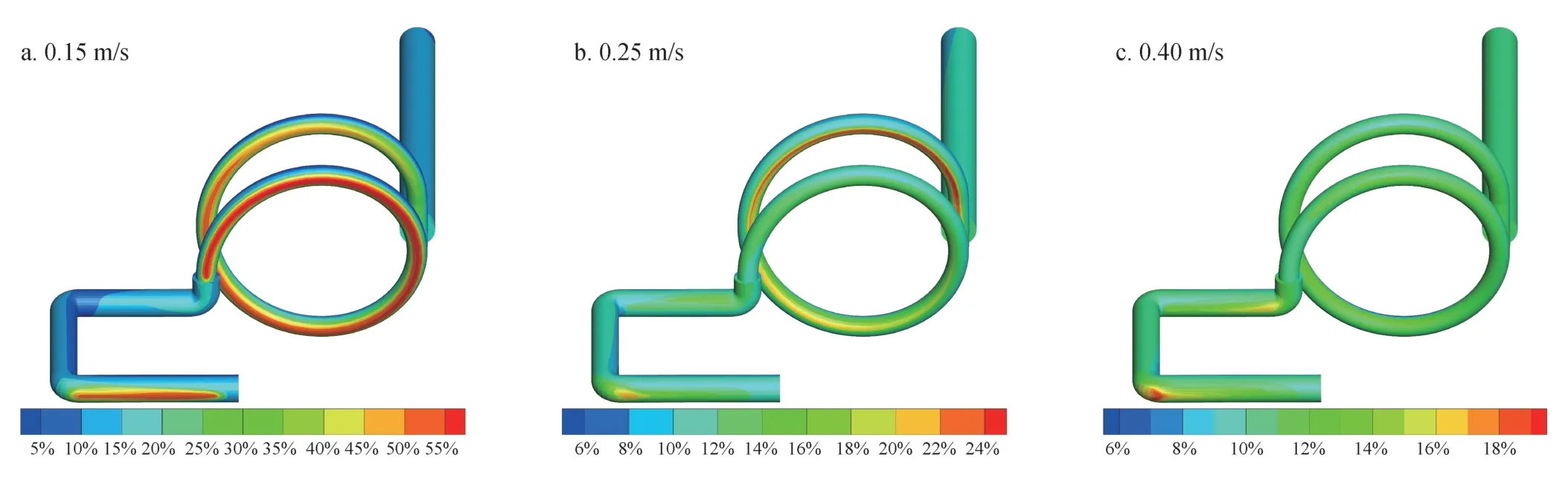
图3 44 μm粒径、10%出砂浓度在不同水速下微米级砂粒浓度分布云图

2.2 微米级砂粒临界不沉积流速的确定

对3种粒径、3种出砂浓度下微米级砂粒在复杂井段内的运移沉积情况进行数值模拟，共获得100多组模拟数据，模拟结果如图4所示。

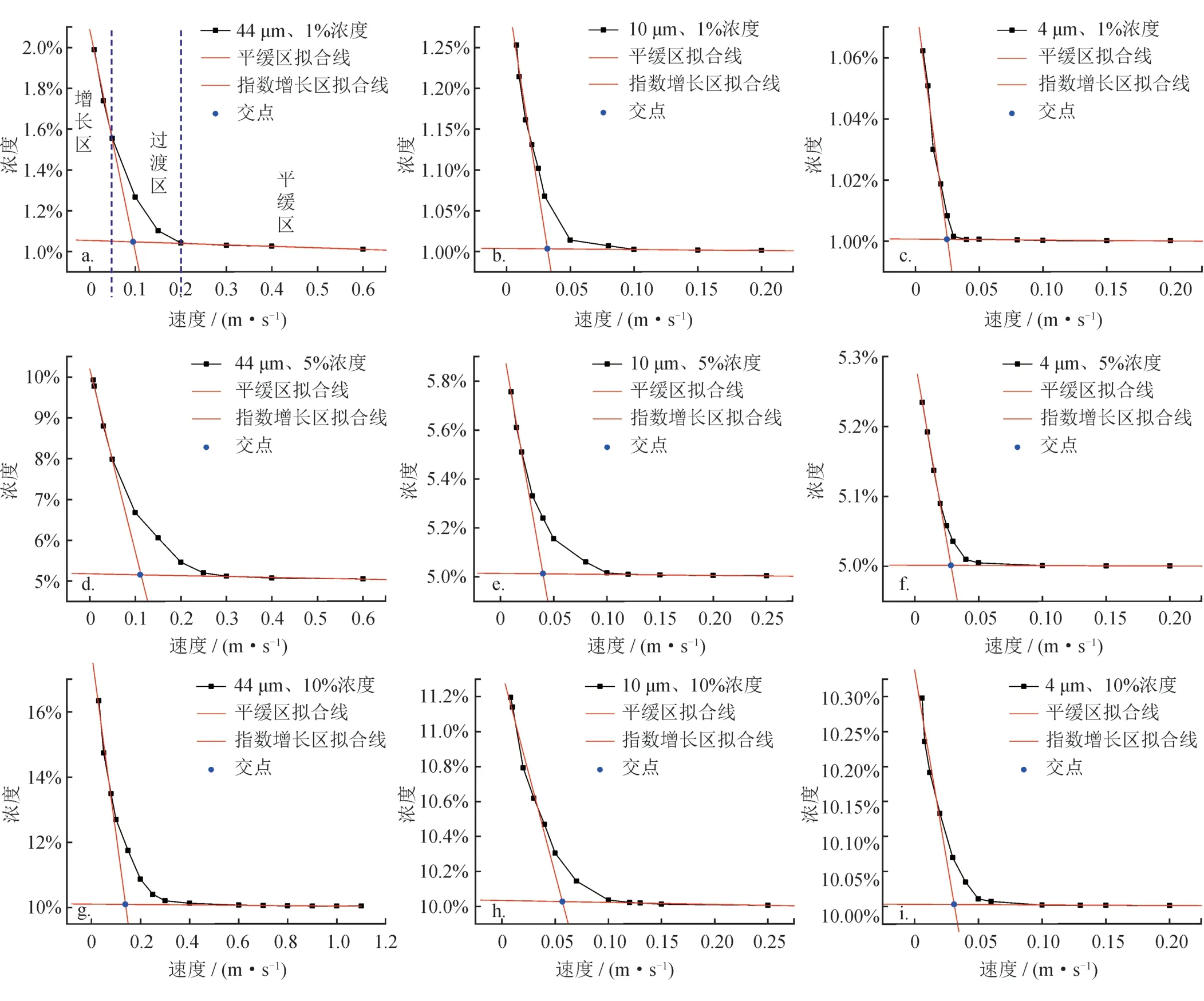
图4 3种粒径、3种浓度下流速与复杂管段内砂粒沉积浓度关系图

以粒径44 μm颗粒1%浓度下，管路内微米级砂粒浓度随水速变化规律为例，由图4-a可以看出，当水速较大时，复杂管段内砂粒浓度无限趋近于地层出砂浓度1%，说明管路内几乎没有砂粒沉降，曲线变化平缓。随着水速的逐渐减小，管路内微米级砂粒浓度逐渐增加，当水速减小到一定程度后，小幅度的速度减小将引起管路内砂粒浓度的急剧升高，浓度呈指数增长趋势。因此可将曲线变化大体划分为3个部分：平缓区、指数增长区以及两者交汇的过渡区。临界不沉积水速位于两种变化趋势交汇的过渡区内。如何确定临界不沉积水速，笔者提出了一种方法：由于临界不沉积水速位于过渡区内，可分别对平缓区和指数增长区进行直线拟合，拟合曲线分别表示两种区域的变化趋势，则这两条直线的交点即为临界点，其横坐标即为临界不沉积水速。水速大于这个值，管路内砂粒沉积量较小，水速小于这个值，管路内的砂粒沉积量将急剧增加，且水速越小，沉积量越大。由此可得到44 μm，1%浓度下微米级砂粒在水合物试采局部复杂井段的临界不沉积水速为0.106 5 m/s。同理，可得到其他工况下的临界不沉积水速，如图4-b～i所示。

2.3 临界不沉积流速结果分析

微米级砂粒临界不沉积水速随粒径及地层出砂浓度的变化规律如图5、6所示。

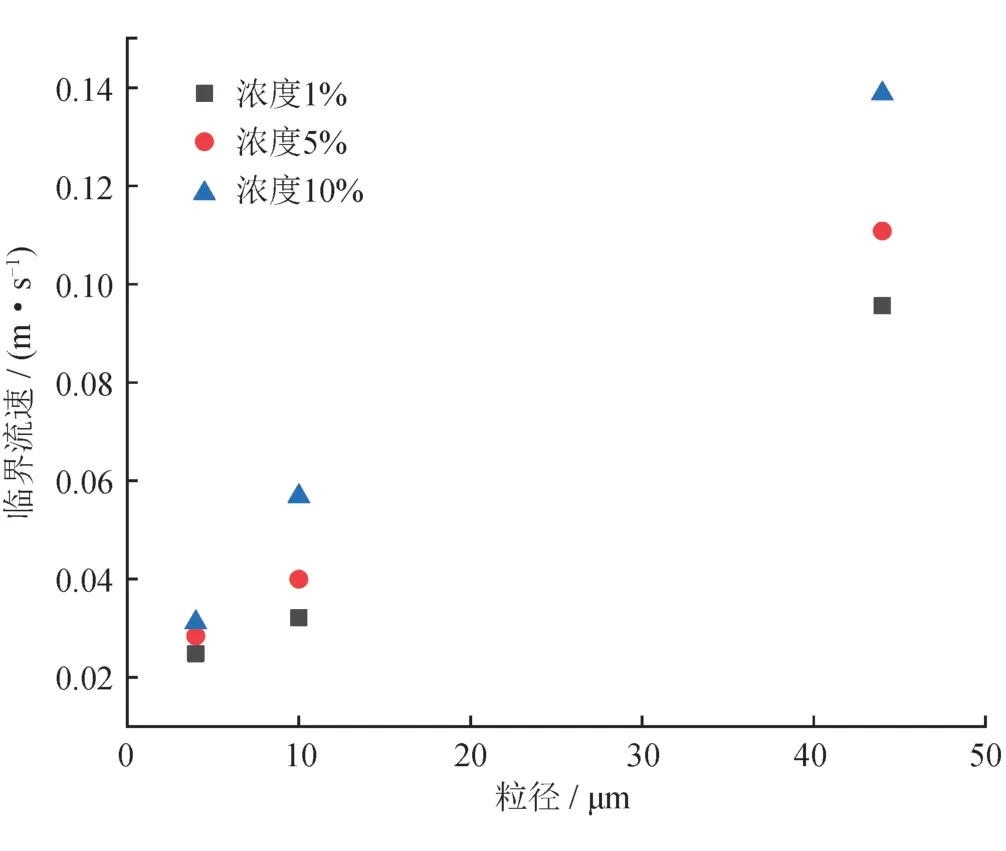
图5 不同地层出砂浓度下临界流速随粒径变化规律图

由图5可以看出，随着粒径的增大，微米级砂粒的临界不沉积水速逐渐增大，粒径较小时，出砂浓度的变化对临界不沉积水速的影响较小，粒径较大时，出砂浓度差别造成的临界不沉积水速的变化变得更加明显。

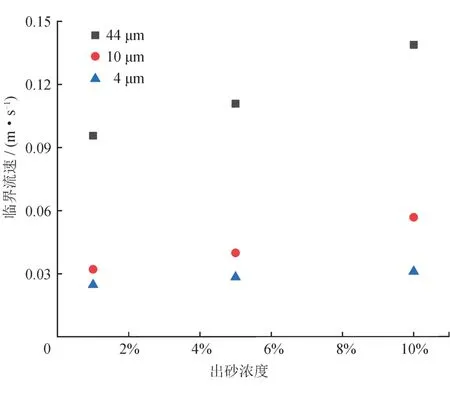
图6 不同粒径下临界流速随地层出砂浓度变化规律图

由图6可以看出，随着地层出砂浓度的增加，微米级砂粒的临界不沉积水速逐渐增加，且浓度较大时，粒径变化造成的临界不沉积水速的变化更大。造成这种现象的原因是因为随着粒径的增大，自重增加，砂粒悬浮需要更大的流速，另一方面，砂粒较小时，比表面积更大，砂粒更易悬浮在溶液中，不易沉降。而且地层出砂浓度越大，井筒内含砂量越多，沉积更容易发生。粒径和地层出砂浓度的双重作用导致粒径较大时，浓度差别造成的临界不沉积水速变化更加明显，出砂浓度较大时，粒径差别造成的临界不沉积水速变化更大。

2.4 微米级砂粒沉积预测模型建立

由于试采局部井段管路复杂，室内实验存在较大难度，数值模拟计算需要耗费较长的时间和计算资源，为获得一种相对便捷且成本较低的计算方式，对上述模拟数据进行分析，水合物试采局部复杂管路微米级砂粒的浓度（C）是地层出砂浓度（C0）、液流速度（v）、液流密度（ρl）、液流黏度（μl）、砂粒粒径（ds）及螺旋段井筒直径（Dlx）的函数，对这些变量进行分析，如表2所示，这些变量之间的数学关系可表示为：

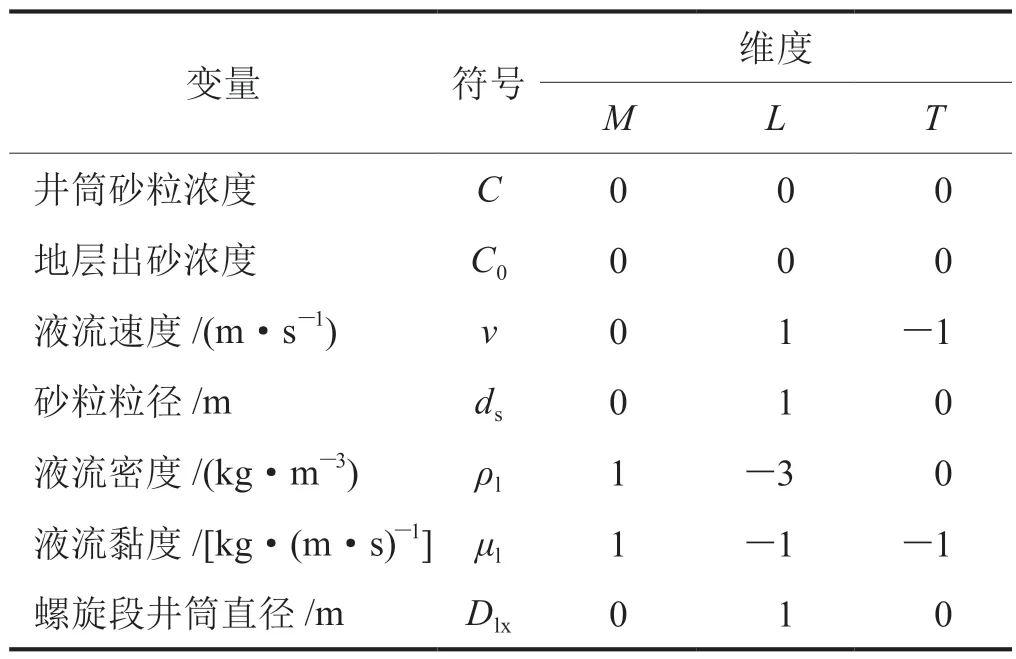
表2 独立变量分析表

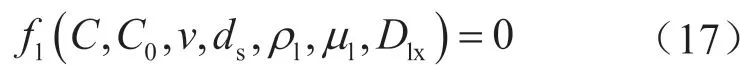
应用Buckingham-Π定理，对上述变量进行无量纲分析，组合成无量纲群，将复杂问题简化为较小组合变量之间的关系。为此定义4个具有实际意义的无量纲量，对所研究变量进行无量纲化。第1个无量纲量为复杂管路井筒内微米级砂粒浓度（π1，C），是因变量，其他变量为自变量；第2个无量纲量为地层出砂浓度（π2，C0），表示地层出砂速率对砂粒沉积运移的影响；第3个无量纲量为（π3，ds/Dlx），代表了粒径对微米级砂粒运移沉积的影响；第4个无量纲量为（π4，ρ1vDlx/μ1）代表了螺旋管雷诺数，式中的特征长度为螺旋管的水力直径，具体如表3所示。

表3 独立变量无量纲化表

4组具有实际物理意义的无量纲量之间的数学关系可以描述如下：

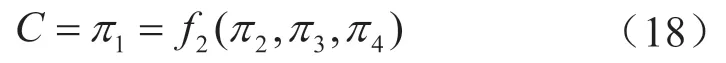
利用OriginPro 2019软件非线性拟合工具对其进行分析，确定拟合方程如下：

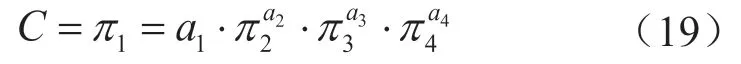
式中a1、a2、a3、a4表示系数。对数据进行拟合，拟合结果如表4所示。

则最终的复杂管路微米级砂粒沉积预测方程为：

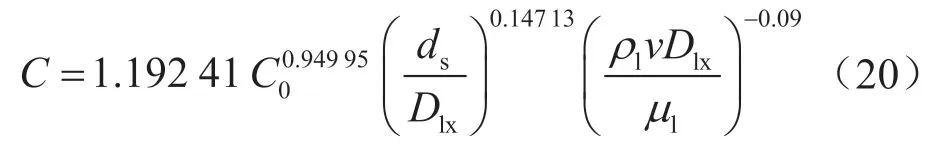
对数据点模型预测值进行统计误差分析来检验模型的准确性。检验模型准确性的统计学参数包括：平均误差（ME）、平均绝对误差（MAE）、标准差（SD）、平均绝对百分比误差（MAPE）、均方根误差（RMSE），这些统计参数定义如式（21）～（25）所示[39]。统计参数分析结果如表5所示。可以看出ME、MAE、RMSE均在0.7以下，SD和MAPE也在9.1以内，结合表4中的相关系数、残差平方和及拟合优度，可以看出模型误差较小。

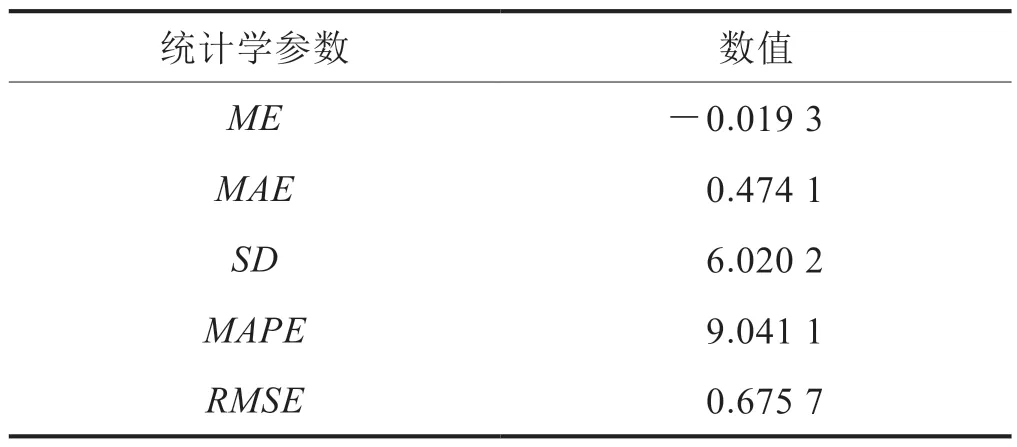
表5 统计参数分析结果表

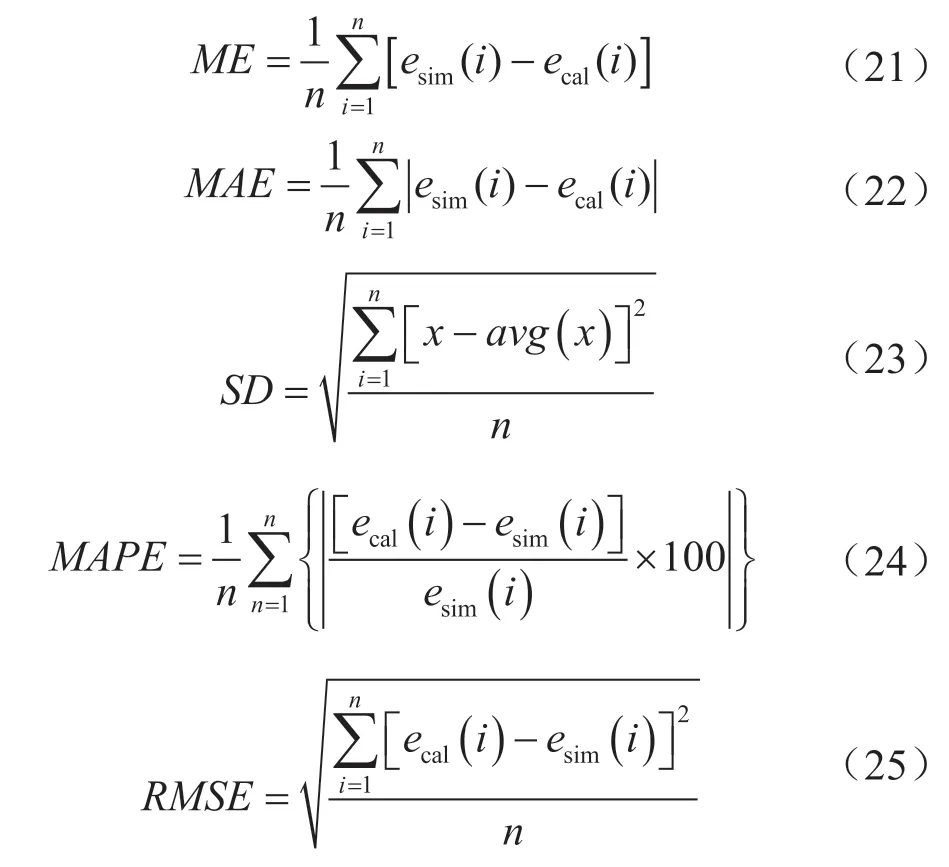
式中n表示模拟的组数；ecal、esim分别表示计算、数值模型的井筒砂粒浓度。

x的表达式为：

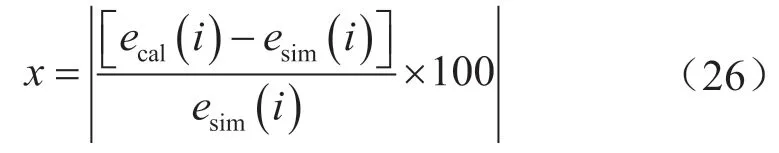
为了更好地描述水合物试采局部复杂井段沉砂的严重程度，方便计算和预测不同条件下的砂粒临界不沉积水速，定义砂沉积浓度比这一概念，即：试采后井筒内的含砂浓度C与地层出砂浓度C0（与降压方式、地层出砂速率等有关）之比。即

当e＝1时，说明进入井筒内的砂量等于运移出井筒的砂量，此时的水速即对应为临界不沉积水速；当e＞1时，说明井筒内有沉积，且e值越大，沉积越严重。

定义砂沉积浓度比后，利用式（20），可计算得到井筒内的沉砂浓度，进一步利用式（27）计算砂沉积浓度比，直观显示井筒内的沉砂情况。另一方面，令e＝1，可以反推计算得到不同情况下复杂管路中的砂粒临界不沉积水速，从而为安全合理安排水合物生产制度、降压幅度提供参考。

3 结论

1）螺旋段内微米级砂粒沉积情况随着水速的增加而逐渐改善，其中螺旋段上部的砂粒清洁难度要大于螺旋段下部。

2）提出了一种微米级砂粒临界不沉积水速的确定方法，得到了3种粒径3种浓度下水合物试采局部复杂管路微米级砂粒的临界不沉积水速。

3）微米级砂粒临界不沉积水速随着粒径和地层出砂浓度的增大而增大，且粒径较大时浓度差别造成的临界不沉积水速变化更加明显，浓度较大时粒径差别造成的临界不沉积水速变化更大。

4） 提出了砂沉积浓度比的概念，当浓度比为1时，井筒内没有砂粒沉积，当浓度比大于1时，井筒内有沉积，且浓度比越大沉积越严重。

5）得到了水合物试采局部复杂井段井筒沉砂浓度预测模型，计算不同条件下的砂粒临界不沉积水速，为安全合理安排水合物生产制度、降压幅度提供有益参考。