基于SVM的2PTMC多分类算法在船舶柴油机故障诊断中的应用
尚前明,杨 烨,王 潇,曹 召,邓晓光
(武汉理工大学 能源与动力工程学院,湖北 武汉 430063)
当前船舶柴油机故障诊断面临的一大问题是故障特征的发现,由于船舶柴油机的特定工作环境使得获得大量有效的故障非常困难。而常规的分类算法包括神经网络都依赖于大量的样本统计数据,当训练样本数量有限时,很难保障模型有着较好的泛化性能。支持向量机算法(SVM)算法通过核函数将特征空间映射到Hilbert高维空间,有效的降低了模型的VC维,满足了结构化风险原则,非常适合训练样本数量较小的学习情况[1]。
1 用于故障诊断的SVM算法
SVM是Vapnik等人基于统计学理论的结构风险最小化规则提出的,其算法本质上是凸二次规划问题。神经网络的算法极值解有可能是局部最优值,而SVM算法的极值解就是最优解,这就使得SVM算法有着较强的学习能力。另外SVM有着很强的推广能力使得在训练样本很少的情况下依然能在测试集中得到很小的预测误差。
由于船舶柴油机特定的工作环境使其故障数据不易获得,而SVM算法可以从小样本训练集中学习,因此将SVM算法应用到只有较小训练样本的船舶柴油机故障诊断中非常合适。算法的实现主要分为模型训练和故障识别2个阶段,具体步骤如下。
1)模型训练过程。主要是让SVM算法根据两类故障样本的特征值和标签值找到支持向量进而确定最优分类超平面。
(1)搜集船舶柴油机的故障数据和正常数据,根据专家知识建立起训练样本集和测试集[Xi,Yi],Yi∈(-1,1)。
(2)根据Mercer定理选择合适的核函数,根据所选择的核函数对训练样本进行预处理。
(3)模型训练,根据找出的支持向量SV建立最优分类超平面,得到分类决策函数f(x)。
2)故障识别。根据训练好的二分类SVM函数对测试数据进行分类。
(1)将测试数据输入到训练好的SVM模型中,得出特征数据X的输出结果。
(2)利用指示函数将输出结果f(x)归在(-1,1)范围内,做出判断决策。
2 基于SVM的2PTMC分类器
最原始SVM算法是一种二分类算法,本质上是通过两类训练样本划分出一条边界,使两类样本最大程度的远离分离边界。因此要将SVM算法应用到多分类故障诊断中,需要在原始的算法上进行一定的改进。目前比较常用的SVM算法解决多分类问题的思路主要有以下2种。

2)OVA方法,即将训练样本分为一对多的类型,这种方法只需要训练m个分类器,但是存在训练样本不均衡的问题。这种方法虽然简单有效,但是可能存在有些样本一直得不到正确分类,即存在分类阴影问题。
这里采用一种适合船舶柴油机带故障优先级的2PTMC算法来解决多分类问题[2]。该方法属于第二类OVA方法的思想构造分类器,根据故障本身特性将故障分为不同优先级。第一级SVM分类器输入全部训练样本,把第一优先级的故障分出,然后剩下的样本输入第二级SVM分类器进行分类,以此类推直到最后一级分类器,完成全部k类故障样本区分。基于SVM的2PTMC算法结构如图1所示,下面给出2PTMC算法的具体实现步骤。

图1 2PTMC算法结构示意图
当需要解决的是一个m类的分类问题时,训练数据样本集为(x1,y1),(x2,y2),…,(xi,yi),其中x∈Rn,y∈[1,2,…,m]。这里定义一个2PTMC结构元组:(F,SVM,TS,P),具体每个元素的含义如下所示。
F=(f1,f2,…,fi,…,fm),F表示所有的二叉树终止点集合,由f1,f2,…,fi,…,fm待识别的m个可能的故障数据集所组成,正常状态的数据集也包括在内,与图中的正常、故障1、故障2等所对应。
P=(p1,p2,…,pi,…,pm),P表示故障分类的优先级组合,决定了SVM的排序方式。一般情况下,优先级根据故障发生的频率来排序,故障发生频率比较高的优先级大,发生频率低的优先级较小。
SVM=(svm1,svm2,…,svmi,…,svmm-1),SVM表示所有svm分类器的组合,当存在m类分类问题时,需要m-1个svm分类模型,其中第i个svm分类器处理的是故障优先级为pi的分类问题。


3 案例分析
作为船舶核心动力装置的船舶柴油机长期工作在高温、高压的恶劣环境下,并且存在运动部件结构复杂、振源多的特点。这就使得船舶柴油机一旦发生故障,不好确定故障具体位置,稍不留意还可能影响船舶正常运营,甚至造成更大的经济损失,危机船员生命安全[3]。传统的故障诊断方法一般有油液分析法、振动信号分析法、转动信号法和热工参数分析法等。船舶柴油机的热工参数比较容易采集,并且热工参数可直接反应出船舶柴油机的工作状态变化,因此可以采用热工参数对船舶柴油机进行故障诊断。本文数据集来自某船舶MAN B&W 7K98MC型船舶柴油机,该型号船舶柴油机为大型2冲程柴油机,广泛应用于大型船舶上,主要技术参数如表1所示。
根据所采集数据的主要故障和MAN B&W 7K98MC型船舶柴油机比较容易发生的故障综合考虑,选取压气机故障、中冷器效率下降、喷油器堵塞、排气管脏堵几种故障模式进行故障分类诊断,验证基于SVM的2PTMC算法在船舶柴油机故障诊断上的可行性。这里根据所采集数据的不同故障发生频率进行优先级排序(不同柴油机可能不同),具体排序方式如表2所示。

表1 MAN B&W 7K98MC型柴油机的主要技术参数

表2 故障优先级分级表
部分训练样本集如表3所示(这里由于页面尺寸原因只放上前7维数据,实际上有15维)。

表3 部分训练样本数据集
1)模型训练。训练SVM分类器采用Python语言编写程序,调用Python库函数中的SVM函数使得编程变得简单可行。SVM模型中核函数的应用可将有限的线性不可分的特征维度映射到更高的维度已获得更好的分类效果。比较常用的核函数有高斯核、线性核、多项式核等。这里选用高斯核函数,作为一种经典的鲁棒径向集核,高斯核有着较好的鲁棒性,抗干扰能力较强。其数学公式如下:
k(x,y)=exp(-δ‖x-y‖2),
其中超参数δ的选取极为重要,δ的大小影响SVM的分类效果,当δ的取值分别为1、10、100时分类效果如图2所示。

图2 δ值为1、10、100的分类效果图
由图2可知,随着δ的增大,分类边界变得越来越复杂,最后分类边界变成一个个独立的小区域。由此可见δ太大,容易造成过拟合问题(即模型的泛化性能变差),所以δ的选取不能太大。
按照上述的故障优先级分别训练SVM分类器,由于实验数据过多且步骤大多一致,这里只给出第一级和最后一级SVM分类器训练结果。
(1)第一级SVM分类器。训练样本为全部样本,其中正常数据样本20组,其他4类故障样本每种20组,全部训练样本为100组。训练采用高斯核函数,在1~10范围内根据试验选取δ的取值。结果显示,当δ=3时可以获得比较稳定的支持向量(SV)个数,为了防止模型过拟合,这里选取δ=3。第一级SVM分类结果如表4所示。

表4 δ =3时第一级SVM训练结果
(2)第四级SVM分类器。训练数据为压气机故障、中冷器效率下降两类故障训练样本集,每种故障20组,共40组训练数据。分类结果如表5所示。
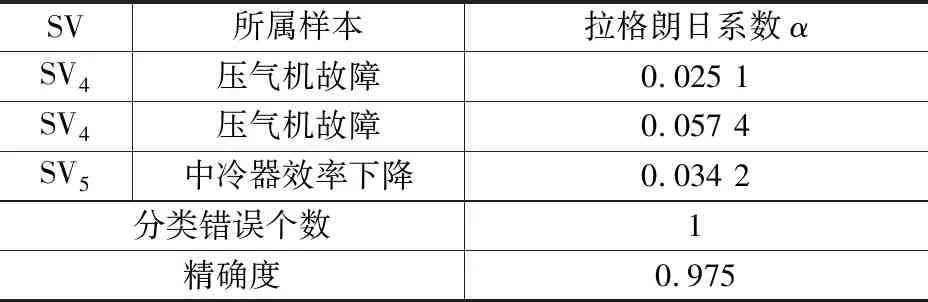
表5 δ=3时第四级SVM训练结果
2)模型诊断。这里采用50组测试数据对模型进行验证,训练结果如表6所示。

表6 测试结果
由表6可知,只有在第二级分类时出现2个错误和第三级分类时出现1个错误。出现错误的原因可能是测试集本身含有噪声或者数据集本身错误,但模型整体分类精确度很高,可以达到分类要求。另外根据测试样本数量可以直观看出,相比传统的OVO和OVA多分类模式,2PTMC多分类方法的样本重复率是最小的,随着数据量的增加,2PTMC算法的优势更加明显。
4 结束语
船舶柴油机由于其特定的工作环境和复杂的结构组成使得其故障原因难以发现和故障数据难以获得。船舶柴油机热工参数的变化可以大体反映其工作过程,本文引用了一种适合小样本决策的基于SVM的多故障诊断算法,并利用此算法根据热工故障对船舶柴油机进行故障诊断。结果表明该方法有效可行,相比于传统的SVM多分类算法,基于2PTMC的多故障分类方法识别精度很高,而且重复样本训练次数明显减少。

