跷跷板式波浪能发电装置运动及载荷分析

周建林，赵江滨，朱风绅，王宇宫，崔天宇

(1.武汉理工大学 能源与动力工程学院，湖北 武汉 430063；2.国家水运安全技术研究中心可靠性工程研究所，湖北 武汉 430063)

波浪能是指海洋中波浪所具有的能量，其能量形式为振动的机械能，可以在几乎没有能量损失的情况下，通过波浪从海洋深处传递到海洋边缘或附近[1]。为了能更有效的利用海洋波浪能，本文提出一种跷跷板式波浪能发电装置。该装置是一种基于横摇运动响应的发电装置，由于该装置波浪能吸收的浮体运动是由波浪直接驱动，因此相比于传统惯性波浪能发电装置，可以更好的吸收波浪能。为使装置发电效率最大化，根据其工作原理，建立数学模型，对装置的运动响应进行分析，并进行仿真模拟，根据结果计算功率，得出最优工况。

1 跷跷板式波浪能发电装置

该装置可以与浮式防波堤相结合，在防浪消波的同时将波浪能转化为电能。图1为跷跷板式波浪能发电装置的示意图。其中图1(a)为单一发电装置的示意图，图1(b)为防波堤与发电装置共同工作时的状态图。

图1 跷跷板式波浪能发电装置示意图

由图1(a)得，跷跷板式波浪能发电装置主要由水面上波浪能吸收浮体、水下的阻尼板以及能量输出装置即PTO(Power Take-off)组成。PTO由阻尼板与浮体的相对运动来驱动，由于运动是在波浪驱动下产生，因此是一个往复的运动。为减少往复运动对齿轮箱及其他传动部件的冲击，提高装置的可靠性，使用1台加装超越离合器的齿轮箱来实现运动方向的改变。此转换齿轮箱可以将输入轴上往复的回转运动转变为单方向的回转运动。

该装置发电工作原理示意图如图2所示，阻尼板位于水下不受波浪作用力影响的区域，向上延伸出一根刚性杆，该杆与阻尼板为刚性连接，通过PTO来实现与上部浮体的连接。当浮体在波浪激振下进行横摇运动时，由于阻尼板位于水下，且阻尼面面积较大，受到的静压力较大，其运动幅度远远小于水面浮体，可以视为静止不动，PTO便可将此相对运动的机械能转化为电能。

图2 工作原理示意图

2 浮体数学模型

2.1 运动分析

通过建立数学模型来计算浮体横摇运动响应及相关影响因素。浮体尺寸示意图如图3所示。浮体详细尺寸参数如表1所示。

图3 浮体尺寸示意图

表1 浮体尺寸参数

浮体在波浪上的横摇运动，从力学的观点看，包括2个方面：一个是刚体运动的力学问题，即浮体作为一刚体在外力作用下，产生运动的问题。船舶在波浪扰动下的横摇运动同周期扰动力作用下的振荡器振动类似。因此研究浮体横摇运动归结为建立浮体横摇运动的微分方程及求解。另一方面是流体动力学问题。浮体在波浪上运动所受到的外力，主要是流体作用力，这些力的大小和变化与浮体以及流体相对运动有关[2]。

根据平衡原理，装置浮体的横摇运动模型可以表示为：

(1)

考虑浮体宽度和吃水有限性对横摇波浪力矩的影响，横摇波浪扰动力矩可以表达为：

Fφ=XφGhα0sin(kx+ωt)，

(2)

式中:Xφ为波面角修正系数，由吃水与波长比、浮体宽与波长比、浮体横剖面形状决定,根据巴甫连柯修正方法得Xφ=0.9；α0为有效波面角振幅；k为波数;x为波浪在横坐标上的位置；ω为波的频率;t为时间。

将式(2)带入式(1)，两边同时除以(Iφ+ΔIφ)得：

(3)

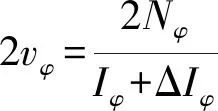
对方程(3)进行求解得：

(4)

本文在借鉴CDP项目分类标准的基础上，参考环保部公布的 《上市公司环境信息披露指南》，并结合样本公司碳信息披露的实际情况，建立了涵盖战略规划、治理架构、风险或机遇识别、碳排放核算四大类的上市公司碳信息披露评价体系。在碳信息披露评价体系的框架下，运用Python软件实现对样本公司所披露文件的内容爬取与文本分析，最后通过算法汇总企业碳信息披露所获得分。碳信息披露评价体系见表1。

由式(4)可知，浮体的最大横摇角度与波面角修正系数Xφ有关。而Xφ=XHφXBφ，XBφ为与浮体宽度有限性有关的修正系数，随着浮体宽度的增加，此修正系数减小。XHφ为浮体吃水有限性的修正系数，随着浮体吃水的增加，此修正系数减小。因此在波浪参数不变，浮体其他参数不变的情况下增加浮体的宽度，浮体横摇角度减小。

2.2 载荷计算

通过改变Bφ以获取浮体在不同工况下的运动响应及波浪载荷情况，根据仿真结果计算浮体所吸收的功率Pb。功率计算公式可由下式表示：

(5)

(6)

式中:Mb为PTO等效阻尼力矩；t1、t2为不同时间点。

3 仿真模拟分析

3.1 计算设置

本文选取波浪参数为：波高H=0.8 m，周期T=3 s，波长λ=14 m。主要针对以下2个方面的仿真计算：①无负载情况下的发电装置浮体的运动响应及波浪载荷;②装置在不同负载阻尼系数下的运动响应情况，估算发电功率，选取最优工况。

跷跷板式波浪能发电装置由水面波浪能吸收浮体和水下阻尼板2部分组成，由于水下静压力较大，阻尼板摆动角度远远小于浮体摆动角度，因此这里将水下阻尼板视为静止不动，模拟理想状况下的运动情况。故在仿真中只分析水面浮体的运动情况和波浪载荷大小。因此这里只对水面浮体进行建模。模型尺寸如图3及表1所示。

根据国际拖曳水池会议(ITTC)建议[3]，对于存在入射波的模拟，入口边界应位于距离船体1～2倍船长处，而出口应位于下游3～5倍船长处，以避免来自边界壁的波反射[4]。为保证重叠网格的重叠区足够大以传递数据，依据波长来设定计算域，入口处位于x轴负方向1λ处，出口位于x轴正方向1.5λ处，宽度0.3λ。出口处10 m设置为波浪消波阻尼区。

为了减少计算时间，xy平面设置为对称平面，选取浮体整体的一半作为计算模型。网格设定3个加密区，分别是水面加密区、背景重叠区、运动重叠区。网格数量如表2所示。

表2 网格划分数量 个

由于本文所提出的装置基于横摇运动，同时为简化计算，这里仅释放y轴的转动与z轴的平动2个自由度，即横摇与垂荡。通过选取不同的阻尼系数来模拟PTO在不同负载情况下装置的做功情况，并根据结果确定装置的最优工况。

3.2 计算结果分析

首先对阻尼力矩系数为0的工况进行分析，即阻尼力矩为0的情况，表示浮体无PTO负载的工况。通过对此工况的计算可以得出浮体在波浪作用下的运动响应及受力情况。图4为水面浮体在波浪作用下波浪力矩、垂向受力、横摇角度，横摇角速度的时历曲线图。

由于软件在计算初期会有一定的波动，因此对6s后的计算数据进行分析。

图4(a)为波浪吸收浮体在无负载工况下所受的波浪力矩图。由图4(a)可得，浮体在周期3 s，波高0.8 m，波长14 m的波浪作用下产生简谐振动。浮体受到的波浪力矩在-3.5 kN·m至3.5 kN·m的范围内波动。图4(b)为无负载工况下浮体在波浪作用下的垂向受力图。浮体在垂向上受到的力由2部分构成，分别是静力和动力，图中曲

图4 无负载工况计算结果图

线表示不含浮体受到静力的情况，即浮体所受动力。图4(c)和(d)分别为无负载工况下浮体在波浪作用下的横摇角度和横摇角速度。浮体在波浪作用下进行往复摆动，最大横摇角度为8°，正方向和负方向的摆动角度相同。浮体顺时针方向的最大角速度为0.20 rad/s左右，逆时针方向为0.35 rad/s左右。当浮体到达最大横摇角度时，角速度为0 rad/s。角速度最大值分别在横摇角度为+2°与-2°时产生。当浮体横摇方向为顺时针时，波浪力做正功，重力做负功，横摇方向为逆时针时，波浪力与重力同时做正功，浮体在逆时针方向的最大角速度大于顺时针方向的最大角速度。

为计算装置在多种不同负载下的发电功率，首先对阻尼系数为5 kN·m·s/rad、7 kN·m·s/rad、9 kN·m·s/rad、10 kN·m·s/rad、12 kN·m·s/rad、13 kN·m·s/rad、14 kN·m·s/rad、15 kN·m·s/rad、17 kN·m·s/rad、20 kN·m·s/rad、25 kN·m·s/rad、30 kN·m·s/rad的几种工况进行计算。并根据结果计算发电功率。

为了方便观察不同阻尼系数对浮体运动情况及波浪载荷的影响，选取2种工况的计算结果进行对比。图5为阻尼系数取13 kN·m·s/rad和20 kN·m·s/rad时水面浮体在波浪作用下受到的波浪力距、垂向受力、横摇角度、横摇角速度对比图。

图5(a)为浮体受到的波浪力矩曲线图，由图5(a)可知，随着横摇阻尼力矩系数增大，浮体所受到的波浪力矩增大，由于阻尼的增大，浮体的横摇角度越小，对波浪的响应越小，与波面位置相差越大，受到的波浪力矩也就越大[5]。图5(b)为浮体垂向受力图，由图5(b)可知，浮体垂向受到的力随着波浪周期呈周期性变化，但是阻尼力矩系数的改变对垂直方向上的受力几乎没有影响。因此，浮体所受到的垂向波浪扰动力与横摇阻尼系数无关。图5(c)、(d)为浮体在波浪作用下横摇角度及角速度的曲线图，从图5(c)可以看出，阻尼力矩系数增大，浮体的角速度减小。阻尼力矩系数的增大导致阻尼力矩增大，浮体在横摇运动时要克服更大的阻尼力矩，因此角速度下降。随着角速度的下降，浮体的横摇角度也会相应的减小。考虑到装置发电是由装置水面浮体与水下阻尼板的相对运动驱动，因此阻尼系数过大时，对装置发电不利。

根据多种工况的计算结果可知，浮体的角速度随着阻尼力矩系数的增大而减小，而表示PTO作用力的阻尼力矩随着阻尼系数的增大而增大，存在最优工况。根据仿真得出的数据，使用公式(5)进行计算，得出浮体在不同阻尼系数下的功率曲线图，见图6。由图6可知，跷跷板式波浪能发电装置的功率随着PTO等效阻尼系数的增大，呈现出先增大再减小的趋势。在12～13 kN·m·s/rad间功率差距较小，阻尼系数在13 kN·m·s/rad时功率达到最大值，输出功率为275 W。当阻尼力矩系数大于13 kN·m·s/rad时，浮体横摇角度下降，角速度下降，功率逐渐减小。

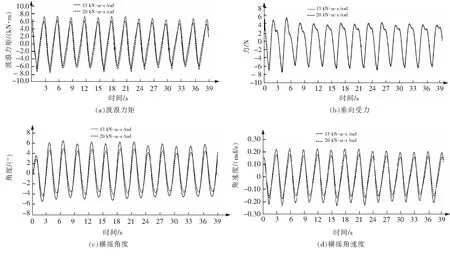
图5 2种阻尼系数工况计算结果对比图

图6 不同阻尼系数下功率图

4 结束语

本文提出了一种跷跷板式波浪能发电装置，该装置通过浮体的横摇运动响应产生电能。根据船舶耐波性的原理对跷跷板式波浪能发电装置的波浪能吸收浮体建立数学模型，通过对数学模型的分析得到浮体运动规律及影响因素，结果表明存在浮体与波浪产生共振的条件，即Iφ+ΔIφ=3 875 kg·m2，装置的运动响应幅度达到最大。阻尼系数、浮体宽度、吃水深度增加，浮体最大横摇角度减小。使用CFD的方法对跷跷板式波浪能发电装置浮体空载工况进行模拟，得出浮体的运动响应及波浪载荷情况，浮体在波浪的作用下进行简谐运动。对不同横摇阻尼系数的工况进行模拟，并根据结果估算发电功率。结果显示，随着阻尼系数的增大，跷跷板式波浪能发电装置浮体吸收的波浪力矩增大，浮体垂向受力保持不变，浮体横摇角速度和最大横摇角度减小。存在最佳横摇阻尼系数使得装置发电功率最大，该横摇阻尼系数为13 kN·m·s/rad，发电功率约为275 W。