从地球到火星回望“洞察号”的飞天之旅
张轩中
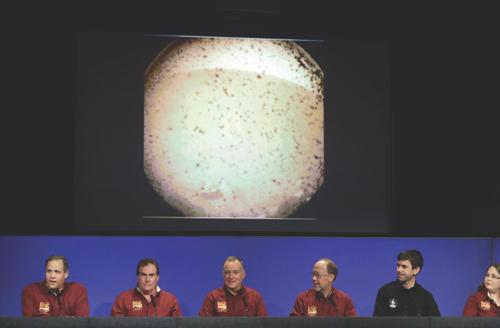


北京时间2018年12月27日,美国国家航空航天局的火星地质探测器“洞察号”在火星表面成功软着陆,并传回了第一张火星表面图。
“洞察号”是为数不多的在火星表面安全着陆的飞行器,之前的美国“火星气候轨道器”和欧洲的“夏帕雷利”探测器都是飞到火星表面就坠毁了。
所以,探索火星并不那么容易,现在“洞察号”已经登陆火星,那么我们可以回望一下它飞往火星的旅程。这一路,“洞察号”一共用了205天到达火星,可是,205这个数字是如何算出来的呢?读了本文,你就会知道。
200天:从地球飞往火星
这几十年来,从地球飞往火星的飞行器有很多,但它们的飞行时间多少有些差别。比如1964年发射的“水手4号”,一共飞行了228天;1974年发射的“海盗1号”飞行器,一共飞了304天;2001年发射的“火星奥德赛号”飞到火星,正好用了200天。
所以,一般从地球飞到火星需要200天左右,这是一种常态。
那么问题来了,为什么不能用1天就飞到火星呢?这200多天的旅行时间是怎么算出来的呢?
这还得从飞行器的运动轨迹说起。
飞出一段“椭圆弧”
从空间的位置来看,地球与火星都围绕太阳做近似的圆周运动,而且,火星的轨道半径比地球的轨道半径要大——以太阳为中心来看,火星在地球的外面,它们的轨道组成了两个同心圆。
火星比地球距离太阳更远一些,由于火星和地球环绕太阳运动的角速度是不同的,所以它们之间的距离会不断发生变化。火星与地球的距离最近时只有5460万干米,而最远时为4.01亿千米。因此如果以光速从地球飞到火星,所需的最短时间只要大约3分钟,而最长的时间大概要22分钟。
而如果飞行器要从地球飞到火星,一般情况下不可能走直线飞过去,而必须要走一个椭圆轨道。如果要走直线的话,需要花费非常多的燃料,这对飞行器来说是 “不堪承受之重”。
那么为什么从地球飞到火星要走椭圆轨道呢?因为飞行器其实可以借助太阳这个“第三者”的力量进行飞行,这听起来有点像太极拳法里的“四两拨千斤”。
对于缺乏物理思想的人来说,可能有一个误解,以为从地球飞到火星就是靠“洞察号”上的太阳能帆板发的电来做动力的。还有一部分人会把电动汽车的概念用到火星探测器上,以为这200多天的飞行,靠的是动力电池产生的能量。其实,这些想法是不对的。
真正把“洞察号”从地球拉到火星的,是太阳的引力。这个旅程其实是“免费”的——因为太阳的万有引力是“免费”的。
正因为太阳的引力,使得“洞察号”从地球到火星的旅行走出一个椭圆轨道,而且,太阳在这个椭圆的焦点位置。这个其实与开普勒的行星运动定律有关。
开普勒行星运动定律
那么,开普勒行星运动定律是怎么发现的呢?
1543年,哥白尼展开关于日心说的工作之后,丹麦的天文学家第谷不太同意哥白尼的观点。他出生于贵族世家,是一个有经济实力来做天文观测的人士。
第谷夜观天象,并且整理了一套看上去杂乱无章的大数据。这套大数据,最后保留着给了他的助手,一个叫开普勒的人。但第谷的本意,好像是想把这套大数据传给自己的女婿的。
那么,为什么第谷最后要把这套大数据留给开普勒呢?
我们可以这样理解,有了大数据,还需要有深度学习的算法,才可以做出人工智能。而开普勒就是那个“人工智能”。开普勒是在合适的时间合适的地点出现的最合适的那个人。
其实开普勒一生生活还是相当潦倒的,虽然生活充满了苦楚,但开普勒依旧是哥白尼的信徒,他坚信日心说的正确性,“洞察号”任务徽章但也没有盲从哥白尼认为行星轨道是正圆形的见解。通过对第谷的天文大数据的深度学习处理,他用“人工智能”的方法得到了行星运动三定律。
第一个定律是很重要的,他认为行星(地球)运动的轨道是一个椭圆,太阳位于椭圆的一个焦点之上。他实际上没有想到,未来会证明,一个封闭的椭圆是一件过于唯美之事,因为根据爱因斯坦的相对论,轨道会有变动,我们不能得到一个封闭的椭圆一一但对于“洞察号”来说,我们还不需要用到广义相对论,因为它离太阳很远,并不是处在强引力场中。
第二个定律异常强大,他几乎用肉眼看出角动量守恒定理,说的是行星(地球)矢径在单位时间扫过的面积相同。
第三个定律,似乎绝对是“上天的旨意”,要从一组数的三次方和另外一组数的平方中看到不变量,依靠一般人的眼睛似乎不够,这个定理说的是行星运动周期的平方和轨道半径的立方成正比。这个定理表明,开普勒就是他那个时代的“阿尔法狗”,是一个计算能力超群的“人工智能”。
这三个定律,迫使牛顿得到万有引力定律。万有引力的出世,其实来自于开普勒对数据的干万次摸排。开普勒的视力不好,相比第谷,他显然不擅长天又观测,但他的确具备从复杂数据中提炼出物理规律的神奇能力。这往往是一种从天上看到人间的天赋异禀。
“洞察号”从地球到达火星的时间,你会算吗?
正因为是靠太阳的万有引力,“洞察号”的飞行时间其实是由太阳对它的万有引力来决定的,对“洞察号”来说,它是“被动飞行”,不是“主动飞行”。换句话说,太阳对它的引力越大,它就飞得越快,飞行速度不是“洞察号”自己可以调节的。这与我们日常生活中开汽车是不一样的,开汽车的时候,速度可以由驾驶员自己控制。这些其实是高中物理中会学到的知识点,不过真正要理解这个事情还需要用到开普勒的行星运动第三定律。
前面已经说过开普勒第三定律,按照这个定律:“洞察号”绕着太阳做椭圆轨道的飞行,其飞行时间的平方与椭圆轨道的半长轴的立方是成正比的。
对于“洞察号”来说,其轨道的半长轴等于火星轨道半径与地球轨道半径之和的一半。
同樣根据开普勒第三定律,地球轨道的半径可以用地球绕太阳的飞行时间表示出来。地球绕太阳一周是365天,这个数据可以转化为地球轨道的半径。
再根据开普勒第三定律,火星轨道的半径可以用火星绕太阳的飞行时间表示出来。火星绕太阳一周是687天,这个数据也可以转化为火星轨道的半径。
有了这些数据,我们就可以再根据开普勒第三定律,计算出“洞察号”绕太阳一周的时间周期,这样就可以计算出“洞察号”从地球飞行到达火星的时间了。