一类具梯度项的拟线性椭圆方程边值问题弱解研究

石 曼，钟金标

(安庆师范大学数学与计算科学学院，安徽 安庆 246133）

目前，关于椭圆型方程边值问题弱解的相关研究一直很热门[1-3]。

文献[1]研究了问题

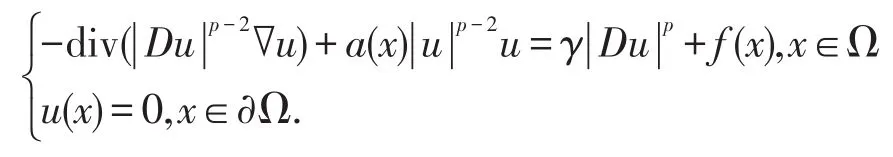
在一定条件下，利用嵌入定理及逼近理论证明了问题存在弱解。张敏[2]研究了问题

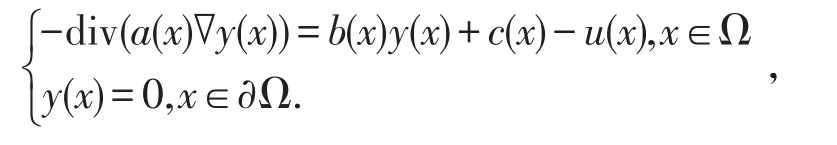
并且利用Sobolev嵌入定理证明了弱解的存在性和唯一性。

钟金标[3]等研究了椭圆型方程组边值问题。利用上、下解方法和不动点定理证明了问题存在弱解。

本文研究问题

其中Ω⊂RN(N≥2)是边界光滑的有界正则区域。我们利用嵌入定理、上下解方法和不动点理论，证明了问题(1）存在弱解，并讨论了解的唯一性。

给定条件：

(H1)设P＜N,N≥2.

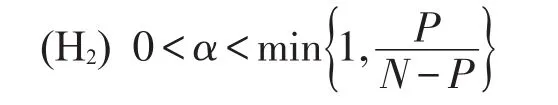
(H3)对任意常数M＞0,当| u(x)|≤M,在Ω中几乎处处成立时，

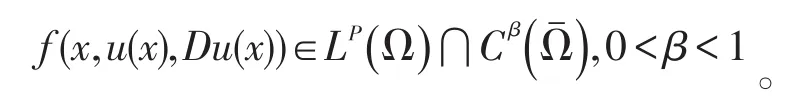
(H4)设 f:Ω×R×RN→R 是Lipschitz连续的，且Lipschitz系数,这里 λ1是 -Δ 算子0-Dirichlet边值问题的第一特征值。

1 主要结果

利用Leray-Schauder不动点定理、文献[6]中定理(10.6）及引理2所证S为紧连续算子知存在使得S(1 , u)=u.即成立：

由f∈LP(Ω ),知u∈W2,p(Ω )。

定理1设(H1），(H2），(H3）成立，则问题(1）存在解

证：由引理3知，存在u(x)∈W2,p(Ω )为下列问题的解：

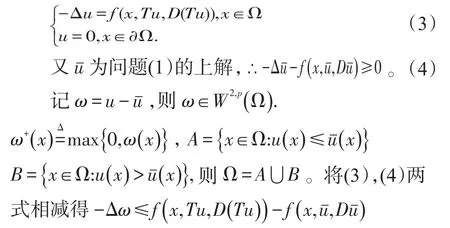
将上式两边乘上ω+后，在Ω上积分，并利用Green第一恒等式得：

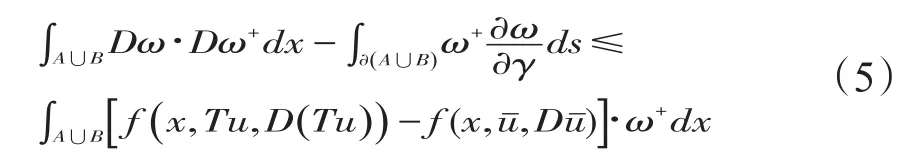
2 唯一性

定理2设(H4）成立，则问题(1）的解唯一。

证：设u1,u2为问题(1)的解，则 u1,u2满足

将(8）中方程两边乘上u1-u2后在Ω上积分，并利用Green第一恒等式得：