含割点或割边的连通图的最大第一修正Zagreb指数
查淑萍,赵舵舵,王 贞
(池州学院大数据与人工智能学院,安徽 池州 247000)
1 引言
设G=(V(G),E(G))是一个简单连通图。n=| V (G)|称为图G的阶,m=| E(G)|称为图G的规模。图G中顶点v的度是指与顶点v相关联的边数,记作degG(v),简记为dv。令G+uv表示在G中两个不相邻顶点u和v间添加一条边后得到的图,G-uv表示在G中删除边uv后得到的图。设X是V(G)的子集,令G-X表示在G中删除X中的点以及所有与这些点关联的边后得到的图。设连通图G为非完全图,u∈V(G),若G-u至少含两个连通分支,则称u为G的割点,类似地,对于e∈E(G),若G-e至少含两个连通分支,则称e为G的割边。J·A·Bundy[1]等对未提及的概念进行了研究。
第一和第二Zagreb指数分别被定义为

它们是由Gutman等人在1972年用于检测分子结构中的电子能量的独立性时提出的。这两类指数是最古老、应用最广的分子结构描述符之一,自提出后受到广大数学化学家们的关注,有关这两类指数的研究成果可查看综述[2-3]及其中的参考文献。
Miličević等[4]在2004年提出修正Zagreb指数的概念,它们是将Zagreb指数中点的度替换为边的度。第一和第二修正Zagreb指数分别被定义为

其中de表示G中边e=uv的度,被定义为de=du+dv-2;e~f表示 e和 f相邻接,即 e和 f在G中有共同的端点。令L(G)表示图G的线图,则由线图及修正Zagreb指数的定义可得
EM1(G)=M1(L(G)),
EM2(G)=M2(L(G)).
A·Ilic-[5]中给出了阶数为n,规模为m的连通图中EMi(i=1,2)的下界,并证明了n阶单圈图中具有最大和最小EMi值的图分别为S′n和 Cn,其中 S′>n为由星图Sn连接两个悬挂点后得到的单圈图,Cn表示含有 n 个顶点的圈。G·F·Su[6]研究了点(或边)连通度至多为k的n阶连通图中EM1的最大(小)值。S·JJi[7-8]等确定了n阶树、单圈图、双圈图以及三圈图中EM1最小和最大图的结构。B·Zhou[9]等给出了EM1与第一和第二Zagreb指数的等式以及不等式关系。本文在以上结果的基础上确定了在含割点或割边的n阶连通图中第一修正Zagreb指数的最大值及达到上界的图的结构。
2 主要结果
引理1[6]设G是n阶连通图,且u,v是G中的顶点,则
(1)若uv是G中的一条边,则
EM1(G-uv)<EM1(G);
(2)若u和v在G中不相邻,则
EM1(G)<EM1(G+uv)。
设Ks和Kt是两个点不交的完全图,u∈V(Ks)且v∈V(Kt)。将u和v黏合后形成的新图,称之为Ks和 Kt的黏合图,记作 Ks(u)·Kt(v),简记为 Ks·Kt。在u和v之间添加一条边后形成的图,称之为Ks和 Kt的连接图,记作 Ks(u)↔Kt(v),简记为Ks↔Kt。
引理2设,若G 是中具有最大第一修正Zagreb指数的图,X是G的全体割点集,则|X|=1。
证明:采用反证法。假设X中至少有两个顶点,则G-X至少含三个块。设G1,G2,G3是其中的三个块。在G中将G2和G3中的点尽可能连边后得到的新图记为G′,则。并且由引理1知,EM1(G′)>EM1(G),这与G的极大性矛盾。从而|X|=1。
引理3设,若G是中具有最大第一修正Zagreb指数的图,v是G的割点,则G-v只含有两个连通分支G1,G2,且G1和G2都是完全图。
证明:假设G-v至少含三个连通分支。设G1,G2,G3是其中的三个连通分支。在G中将G2和G3中的点尽可能连边后得到的新图记为G′,则,由引理1知,EM1(G′)>EM1(G),这与G 的极大性矛盾。从而G-v只含有两个连通分支G1,G2。再次由引理1知,G1和G2都是完全图。类似于引理1.1-1.3的证明,可得如下引理。
引理4设,若G是中具有最大第一修正Zagreb指数的图,e∈E(G)是G的一条割边,则e是G的唯一割边,G-e只含有两个连通分支并且这两个连通分支都是完全图。
定理5设,则
EM1(G)≤(n-2)(2n3-14n2+35n-31),当 且 仅 当G=Kn-1·K2时等式成立。
证明:设Gmax是中具有最大第一修正Zagreb指数的图,则由引理1.3知,Gmax=Ks·Kt,其中s+t=n+1。不防设s≥t≥2。若t≥3,由第一修正Zagreb指数的定义,可得
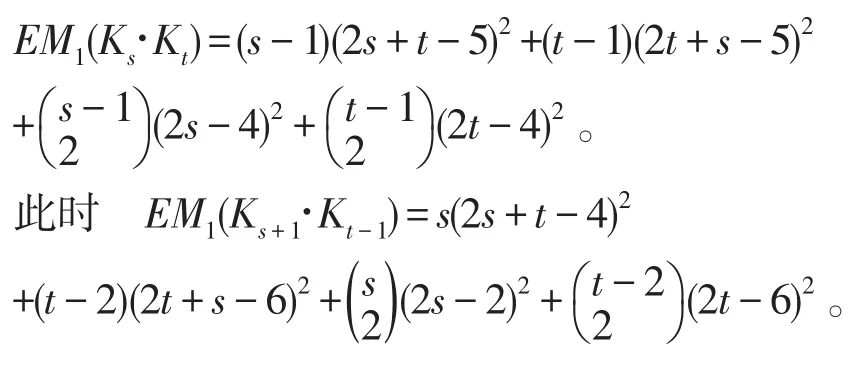
通过计算,可得
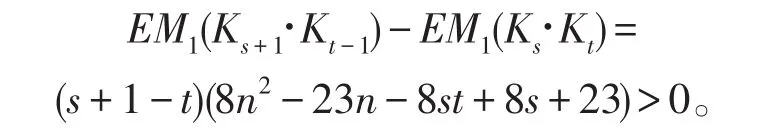
这与Gmax=Ks·Kt的极大性矛盾,从而t=2,进而s=n-1。经计算
EM1(Kn-1·K2)=(n-2)(2n3-14n2+35n-31),定理得证。
定理6设,则
EM1(G)≤(n-2)(2n3-14n2+35n-31),当 且 仅 当G=Kn-1↔K1时等式成立。
证明:设Gmax是中具有最大第一修正Zagreb指数的图,则由引理1.4知:
Gmax=Ks↔Kt,其中 s+t=n。不防设s≥t≥1。若t≥2,由第一修正Zagreb指数的定义,可得
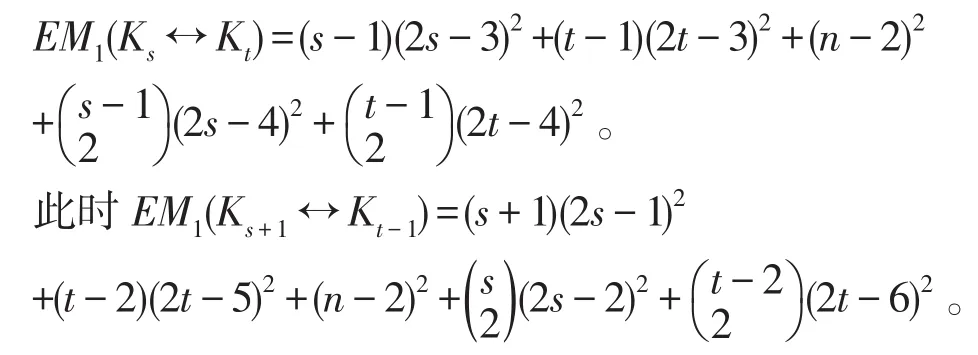
比较两式的差,可得
EM1(Ks+1·Kt-1)-EM1(Ks·Kt)=2(s+1-t)(4n2-17n-4st+4s+22)>0.这与 Gmax=Ks↔Kt的极大性矛盾,从而t=1,进而s=n-1。经计算EM1(Kn-1↔K1)=(n-2)(2n3-14n2+35n-31),即证。

