湖南省房地产市场价格影响因素实证研究
韩 翔,杨 力
(安徽理工大学 经济与管理学院,安徽 淮南232001)
一、引言
进入21世纪,随着房地产市场化改革的不断深入,房地产业的发展突飞猛进,其在国民经济中的地位越来越强,与此同时,城市房价的过快增长所带来的供需不平衡现象越来越明显。房地产价格不仅关系到一般老百姓的生产和生活问题,还关系到一个城市发展的潜力,更关系到整个国民经济的稳定性。宏观经济基本面的变化会影响人们对未来的期望,从而产生房地产市场供需力量对比的失衡,进而引起价格的上升或下降。我国幅员辽阔,各地区发展不均衡,房地产产品又具有空间不可移动性,所以房地产价格因时因地而异。以北上广深为首的一线城市,其平均房价甚至超过一些国际大都市;而相当一些三、四线城市,大量楼房却无人问津。因此,了解房地产与社会经济活动的关系十分必要。
近年来国家房地产政策连续变更,从“新国八条”到“国五条”,由“去库存”到“限购”,使得各地房地产价格跌宕起伏。显然,房地产价格已经成为社会广泛关注的焦点。面对国家的宏观调控,具体到各省份的实际情况,究竟哪些因素对房价有显著影响?这正是本文主要解决的问题。
针对房地产价格影响因素,国内外学者们做了大量的研究。国外方面:丹尼斯·迪帕斯奎尔和威廉·惠顿在2002年出版的《城市经济学与房地产市场》一书中指出经济增长与利率的调整对房地产市场价格有显著的影响[1];Elbourne利用脉冲函数为研究方法,得出货币供给的变动对英国房价有正向影响的结论[2];Elod通过分析多国房价情况,认为人口因素与房价有显著关系[3]。国内方面:张红在《房地产经济学》一书中指出商品房销售面积的变动会导致房价的变化[4];崔光灿通过分析我国31个省份的相关数据,发现利率和通货膨胀率对我国房价有明显的影响[5];王鹤用空间计量方法分析我国东部、中部、西部地区房价的差异,指出商品房销售面积、人民币汇率等因素对房地产价格有影响[6]。国内外学者的研究主要分析了各因素单独对房价的影响,而根据对国家统计局相关指标的分析,各指标的变化两两间对房价有着不同的作用。同时,地域的不同,因素的影响也不尽相同。
根据中国统计年鉴和湖南省统计年鉴公布的相关情况,湖南省房地产2016年商品房销售面积达到8 085.36万平方米,27.1%的增速创历史新高,远高于全国的22.46%;人均居住面积44.00平方米也高于全国平均水平36.60平方米;但52.75%的城市化率却明显低于全国的57.35%。从湖南省自身来看,房地产贷款余额7 077.86亿元,占全部贷款比重的25.7%,增速同比达到29.7%,高出全部贷款增速16个百分点。湖南省房地产市场的这些表现或多或少成为造成房价上涨的原因。
因此本文通过相关数据的对比以及考虑数据收集的完整性,结合相关学者的研究,选取最常用的宏观调控指标及最能反映地域性特点的5年期以上贷款利率、货币供应量、湖南省城镇人均居住面积、湖南省城市化率、湖南省商品房销售面积5个指标作为解释变量,湖南省商品房销售均价作为被解释变量,借助Eviews 8.0软件通过对数变换模型结合Shapley值与Roubens模糊测度定量分析湖南省房地产价格的影响因素及其影响程度与交互作用。
二、研究方法
(一)双对数模型
对数变换是一种数据变换方式,其目的是让数据能够符合我们所做的假设,使我们能在已有理论上对其进行分析,因此双对数模型被广泛应用于弹性研究。
时间序列数据的平稳性是回归模型建立的前提,否则将出现伪回归的问题,使得模型不能反应被解释变量与解释变量之间的真实关系。
综上所述,本文基本模型设定为:

其中,Yt表示被解释变量,C表示常数,X1t,X2t,…,Xnt表示各解释变量,β1,β2,…,βn表示各解释变量的系数,εt表示随机残差。
(二)Shapley值
L.S.Shapley在合作博弈理论中给出了解决n人合作对策问题的方法,称为Shapley值法[7]。Shapley值正是依据个体对全局的边际贡献期望值来度量个体在全局中的重要程度。由于单个准则的全局重要程度不仅凭单点集的测度值决定,还应包括属性子集的测度值变化大小,因此人们采用Shapley值来度量属性的重要程度。
设I={1,2,…,n}为n个合作人的集合。若对于I的任何子集s包含于I都有一个实数v(s)与之对应,且满足:
(a)v(ø)=0,其中ø为空集;
(b)对于任意两个不交子集s1、s2包含于I,都有v(s1∪s2)≥v(s1)+v(s2),则称v(s)为定义在I上的一个特征函数。
L.S.Shapley证明了此函数需满足对称性、有效性、冗员性、可加性,即合作贡献的多少不随每个人在合作中的记号或次序变化;合作各方贡献总和等于合作贡献;如果一个成员对于任何他参与的合作联盟都没有贡献,则他的贡献为0;有多种合作时,每种合作的贡献大小与其他合作结果无关。此函数可以表示为:

其中,Si是I中包含成员i的所有子集形成的集合,|s|是集合s元素的个数,w(|s|)是加权因子且:

(2)式中,v(s)-v(s{i})表示成员i在他参与的合作s中所做的贡献,这种合作共有(|s|-1)!(n-|s|)!种出现方式,因此w(|s|)为每种方式出现的概率。
(三)Roubens交互测度
基于模糊测度,M.Roubens提出了测度间交互作用的计算方法,称为Roubens交互测度[8]。对于元素i,j∈I,Roubens交互测度可以表示为:
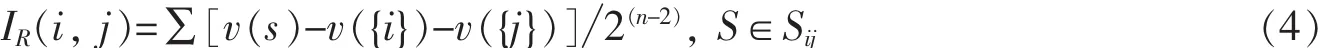
其中,v(s)代表i,j所共同参与的合作所做的贡献。
Roubens交互测度表示将联盟中任意两个个体加入可能的联盟产生的特殊平均增加值。若测度值大于0,则表示两个个体产生积极的交互作用;若等于0,则表示两个个体是独立的;若小于0,则表示两个个体之间产生消极的交互作用。Roubens交互测度考虑了一个准则在整个准则集中的全局交互作用,相比单独考虑测度值无疑更加合理。
三、实证分析
(一)数据来源
指标数据来源情况如下:5年期以上贷款利率(简称利率)采用央行公布的调整前后利率水平的实际执行天数平均而来;货币供应量(简称准货币)采用M2与M1之差,数据来源于中国统计年鉴;湖南省城市化率(简称城市化率)、湖南省人均居住面积(简称居住面积)、湖南省商品房销售面积(简称销售面积)和湖南省商品房销售均价(简称平均房价)均来源于湖南省统计年鉴,时间跨度为2005年至2016年。
(二)平稳性检验
平稳性检验的目的是避免出现伪回归。时间序列的平稳性检验一般通过ADF检验来完成。ADF检验是检验时间序列是否具有单位根,如果存在单位根则该时间序列为非平稳序列,否则为平稳序列。原假设为H0:r=0,即存在单位根。
用Eviews 8.0软件处理取对数后的原始数据,得出结果如表1所示。

表1 不同显著性水平下的平稳性检验表
由表1所示结果可知,level条件下所有变量t值均小于显著性水平临界值,未通过ADF检验,即都是非平稳时间序列,因此原假设成立。
于是对原时间序列进行一阶差分再次进行平稳性检验。通过对比t值与显著性水平临界值,一阶差分时间序列平均利率在1%水平下通过ADF检验,准货币、居住面积、销售面积、平均房价在5%水平下通过检验,城市化率未通过ADF检验。所以城市化率为非平稳时间序列,其余变量为平稳时间序列。因此剔除变量城市化率,其余变量称为一阶单整时间序列。
(三)协整检验
协整的概念是由Engle和Granger于1987年正式提出[9],这使得研究多变量之间的均衡关系变得可能,也使非零阶单整变量的回归变得有意义。对于非平稳的时间序列,其线性组合却有可能是平稳的,这就是协整检验的目的。
EG两步法协整检验,就是用OLS回归估计同阶单整变量的回归方程,从而得到残差的时间序列,然后对残差的时间序列进行平稳性检验。H0:r=0,则存在单位根,为非平稳序列,即被解释变量与解释变量间不存在协整关系,否则拒绝原假设。估计结果如表2所示。

表2 协整检验表
由表2可知,残差的时间序列在5%水平下通过ADF检验,因此拒绝原假设,即被解释变量与解释变量间存在协整关系。
(四)方程的确定
综合(1)式与检验结果,建立双对数模型为:

对模型进行OLS回归,其中T检验的假设为H0:r=0,即解释变量的系数为0。表3的回归结果显示解释变量均通过了T检验,其中平均利率和准货币显著性水平小于1%,居住面积和销售面积显著性水平小于5%。模型调整后的R方为0.996 270,接近于1,模型的拟合度很好,同时DW值在2附近,无明显自相关性。因此拒绝原假设,被解释变量与解释变量整体的线性是平稳的。

表3 模型回归分析表
由于本文只考虑主要因素对房价的影响,因此不考虑常数项与随机残差。需要强调的是影响房价的因素有很多,常数项与随机残差项恰好可以表示为其他影响因素。综上所述再结合(1)式确定方程为:

其中,Yt为被解释变量平均房价,解释变量X1t为利率、X2t为准货币、X3t为居住面积、X4t为销售面积。
方程的数学意义在于:其他条件不变的情况下,利率每变化1%,房价变化0.37%;准货币每变化1%,房价变化0.28%;居住面积每变化1%,房价变化0.38%;销售面积每变化1%,房价变化0.27%。
从经济学上解释则表现在:利率的上升,造成房地产开发企业的成本提高,从而使房价上升;准货币的提高则说明,房地产投资仍然受到追捧,促使房价持续上升;房价随人均居住面积的提高而提高,表示人们对改善生活水平,提高生活品质仍有需求,因此拉动房价上涨;而商品房销售面积的正相关则代表供给方面市场的火热,推动着房价走高。
(五)Shapley值与Roubens交互测度的求解
各解释变量对房价的影响不仅与对应的回归系数有关,还应考虑它们自身的分布特点。相关程度越高(即回归系数越大)影响越大,离散度越大影响越大。基于这两点,综合考虑各解释变量的回归系数和离散度对回归方程进行Shapley值的分解,其中离散度用赫芬达尔指数[10]度量记为H。H的计算方式为:

求解基本原理为:先将各解释变量实际值带入前面确定的方程中,求出房价的实际水平,然后运用赫芬达尔指数;再将某一变量的平均值与其他变量的实际值或平均值带入方程中,分别求出房价的估计水平,然后运用赫芬达尔指数;实际水平与各估计水平之差即为解释变量各种组合方式的贡献;再运用(2)式求出各解释变量的边际贡献总和,即为该变量的Shapley值。
Shapley 值的求解计算量较大,因此不予赘述。 结合(2)式、(3)式、(6)式、(7)式,得出贡献率分解结果,如表4所示。

表4 影响因素贡献率表
从表4数据可知,影响湖南省房价的4个主要因素贡献度十分接近。单个来看,5年以上贷款利率对房价的贡献整体呈下降趋势,这与2005年至2016年这段时期国家对贷款利率向下调低相吻合。准货币的贡献逐年上升,则表明其对房价的影响越来越大。商品房销售面积和人均居住面积的贡献在稳定的区间内波动,时高时低。用平均贡献率表示各自权重,则有Is(利率)=0.249 1,Is(准货币)=0.250 1,Is(居住面积)=0.250 7,Is(销售面积)=0.250 1。
通过(4)式测出各因素两两间交互测度为:IR(利率,准货币)=0.174 7,IR(利率,居住面积)=0.170 9,IR(利率,销售面积)=0,IR(准货币,居住面积)=-0.161 7,IR(准货币,销售面积)=0,IR(居住面积,销售面积)=0。这说明商品房销售面积与其他因素彼此独立;利率与准货币间有着积极的协同作用;利率与居住面积也有着积极的协同作用;准货币与居住面积为消极的协同作用。也就是说利率与准货币或者利率与人均居住面积的同向变动会加剧房价的变动,而准货币与居住面积的同向变动会降低房价的变动。
四、结论与建议
本文的相关论证表明湖南省房地产平均价格与5年期以上贷款利率、准货币供应量、湖南省人均居住面积、湖南省商品房销售面积均为正相关,且这4个因素对房价的影响十分接近。这说明国家的宏观调控与湖南省自身的供需情况对房价有着同等重要的影响。而根据湖南省2016年的统计年报,湖南省房地产市场仍然有着庞大的潜在供应规模,与此同时市场上销售监管的普遍不规范造成国家的限购政策被扭曲为“房源紧张”,导致房价被恶意哄抬。准货币量的增大表明房地产市场已经有了潜藏在表面投资热背后的泡沫,作为国民经济的重要组成部分,湖南省房地产市场价格的不平稳势必对湖南省国民经济产生负面影响。
为此,对稳定房价提出如下建议:当国家下调贷款利率的同时,湖南省政府可以通过发展房地产以外的其他行业以吸引消费,从而使M1获得增长而降低M2与M1之差,以达到降低房价或是降低其增长速度的目的。从人均居住面积这方面看,可以通过增加大户型房产的税收来调整购房的盲目性。而最重要的是加强房地产销售的监管,避免政策被扭曲执行,从而使商品房销售面积这一最直观的指标更能反应市场真实的情况,使政府可以通过市场真实的供需情况制定合理的政策,最终达到房地产市场稳定发展的目的。
房地产市场价格影响因素是多方面的,各因素的重要程度不完全相同,也很难通过其中某一因素的变化来判断市场的变化。因而本文通过Shapley值与Roubens交互测度结合回归方程来分析湖南省房地产市场价格影响因素是合理的。值得完善的是本文选取的数据是以年度为时间段的,如果能把时间段精细到季度或者月份,同时能收集更多完整的指标数据,可以将湖南省房地产市场价格影响因素分析得更加全面。

