超临界CO2水平螺旋管内对流换热的数值模拟
,,
(河北科技大学 机械工程学院,石家庄 050018)
0 引言
以二氧化碳工质作为制冷剂的跨临界热泵机组,因其对臭氧层无破坏(ODP=0)、温室效应潜能极小(GWP=1);系统稳定性高、安全性好、结构紧凑、占用空间小;并且具有较高的制热能效比而引起广泛的关注与研究[1-8]。近年来,为充分发挥热泵热水器高效、节能和环保的特点,CO2作为制冷剂再次引起了行业的重视,并且在我国发展迅速,具有良好的经济效益和社会效益,如何提高CO2作为制冷剂在热泵系统中的换热性能便成为了重点研究方向。近年来,超临界CO2在换热管中的研究颇多,其中,更多的是针对直管中的换热特性和阻力特性研究[9-11],而其在螺旋管中的流动换热的研究相对较少。
Zhang等[12]采用数值模拟的方法,研究了超临界CO2在水平圆管内的对流换热特性,并与工质水在水平圆管的流动进行了对比,结果表明,超临界CO2的边界层更薄、粘度更低、比热容更大,从而使超临界CO2有更好的换热效果。靳遵龙等[13]采用Y-S低雷诺数模型对超临界CO2在直径100 μm的水平管内冷却对流换热特性进行了数值模拟,结果显示,对流换热系数随进口雷诺数的增大而增大,换热系数峰值出现在CO2准临界温度点附近。杨传勇等[14]采用数值模拟的方法,研究了超临界CO2在直径0.5 mm、长度1 000 mm的各种倾斜角度的直管中的冷却对流换热性能,并研究了浮升力对换热的影响。王淑香等[15-16]研究了超临界CO2在竖直螺旋管中的流动换热特性,结果表明,沿程换热系数先上升、后下降,热边界层变薄是换热强化的主要原因,比热容和导热系数下降是对流换热系数减小的主要因素。李洪瑞等[17]以RNGk-ε湍流模型对超临界CO2流体在内径9 mm、长度5.5 m、节距32 mm、绕径283 mm的竖直螺旋管中的流动换热进行了数值模拟,并将CO2管中流动方向对换热的影响进行了研究,结果表明,浮升力对螺旋管上下流动方向上的流动换热性能影响不大,对水平流动的影响较大。刘新新等[18-19]采用数值模拟的方法研究了超临界CO2在水平螺旋管中的流动换热性能,并研究了质量流量、热流量以及压力对换热系数的影响,结果表明,超临界CO2在水平螺旋管中的换热系数大于CO2在水平直管中的换热系数,换热系数随质量流量的增加而增大;在似气体区,换热系数随着热流量的增加而增大,而在似液体区,热流量对换热系数几乎没有影响;换热系数峰值点随着压力的升高而下降,并向高温区偏移。
上述文献中对螺旋管的研究大多集中于超临界CO2的参数变化对流动换热的影响,而未提及螺旋管的结构参数对超临界CO2管内流动换热的影响。本文在前人研究的基础上,建立水平圆直管和水平螺旋管的物理模型,对比分析其换热的特性及其重力对其影响;并以螺旋管为基础,研究管径、节距对超临界CO2流动换热的影响。本文研究可为水平螺旋管在CO2热泵气冷器中的应用和选取提供科学依据。
1 物理与数学计算模型
1.1 物理模型
水平螺旋管的基础模型如图1所示。螺旋管的具体参数如下:螺旋管直径d=4 mm,螺旋半径Rc=40 mm,管长L=2 000 mm,节距2πb=10 mm,螺旋管曲率δ=0.1;壁面采用等热流密度,且采用无滑移边界条件。

图1 水平螺旋管的物理模型
为了研究螺旋管的结构参数对超临界CO2换热特性及湍流度的影响,建立了5组模型,其结构尺寸如表1所示。

表1 5组螺旋管模型的结构尺寸
1.2 数学模型
本文采用的是RNGk-ε湍流模型,其较标准k-ε湍流模型在更广泛的流动中有着更高的精度,对于弯曲流线型能够更好地处理。该模型包括连续性方程、动量方程、能量方程,具体如下。
连续性方程:
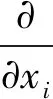
(1)
动量方程:

(2)
能量方程:

(3)
1.3 网格划分及求解设置
通过Solidworks建立三维几何模型并导入ansys meshing中进行网格划分,由于近壁处速度和温度梯度变化较大,因此,采用Automatic Method方法对管壁设置膨胀层以加密网格。综合考虑计算的精度以及计算所需的时间,4 mm螺旋管的网格数在2×106~3×106,6,8 mm螺旋管的网格数在3×106以上,划分的网格如图2所示。原始模拟工况为压力P=8 MPa,热流密度q=30 kW/m2,质量流速G=250 kg/m2·s,入口温度45 ℃。文中所有工况皆采用CFD软件Fluent模拟计算,模型采用变物性,不同温度和压力下的超临界CO2的热物性参数通过Refprop 9.0[20]获得,模拟中的CO2热物性参数按照piecewise-liner方法输入,节点数取8个。压力和速度耦合采用SIMPLEC算法,动量和能量方程采用二阶迎风格式的差分方法,进口边界条件采用质量流量入口,出口边界条件采用自由出流,壁面为恒热流边界。

图2 螺旋管网格划分示意
1.4 数据处理
管道内截面流体温度Tf和换热系数h分别为:
(4)
(5)
式中q——壁面热流密度,W/m2;
Tw——截面的周向平均壁温,K。
2 结果分析与讨论
为验证模型的准确性,数值模拟工况采用王淑香等[15]的试验工况,且根据试验采用螺旋管等比例建模,并将截面流体温度Tf与截面周向平均壁温Tw的数值模拟结果与试验结果进行了对比,如图3所示。可以看出,沿程截面流体温度的试验值与模拟结果基本吻合,而沿程壁温在s/d为250~450之间的模拟值稍低于试验值,其他区间吻合程度也较高。考虑到试验测量误差,故可以认为模拟值能较好地反映试验值的大小,证明了数值模拟模型的可靠性。

s-流程;d-螺旋管内径;s/d-流体在管内的位置
2.1 超临界CO2在管内的冷却换热特性数值模拟对比
为探究超临界CO2在直管和螺旋管中的换热性能,分别对管径4 mm、有效长度2 000 mm的直管和螺旋管进行了模拟。图4示出相同质量流量、入口压力和热流密度下,超临界CO2在直管和螺旋管内平均换热系数的模拟计算结果。从图中可以很明显地看出水平螺旋管的对流换热系数大于水平直管,并且高出水平直管15%。可见,水平螺旋管内流动湍动更为剧烈,换热更强,换热系数更高。另外,可以发现,直管和螺旋管中的换热系数皆在准临界点附近出现极值点,这是因为超临界CO2的物性随压力和温度变化剧烈,其比热容在准临界点附近出现最大值。
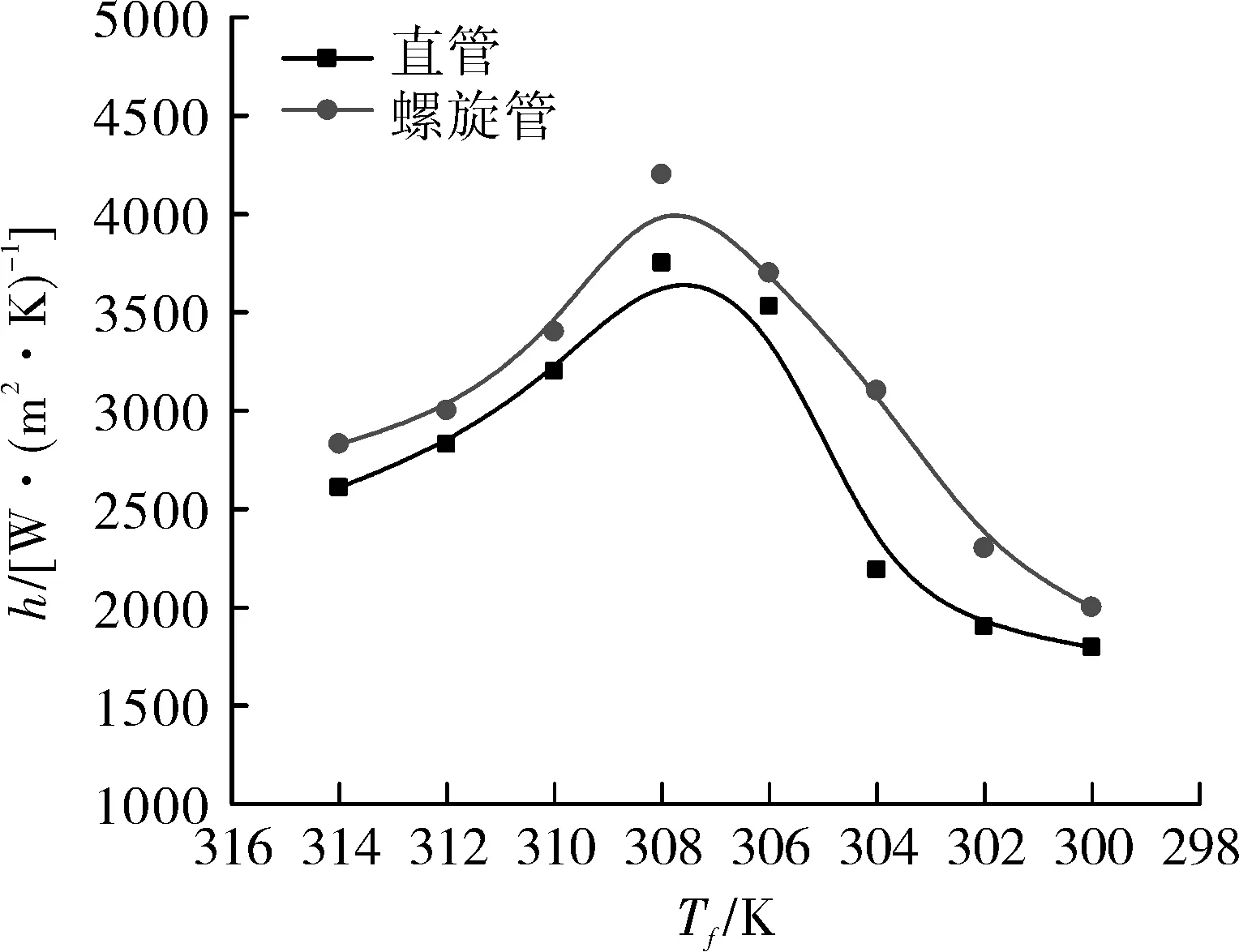
图4 直管和螺旋管换热系数模拟值的对比
各管长中间截面上(s/d=250)的流体温度分布如图5所示,可以看出:(1)主流区与壁面附近的流体之间产生密度差,并且壁面附近的流体逐渐被冷却;(2)主流区的高温流体偏离截面中心并向管顶和管外侧移动,造成主流区与壁面区之间的密度差不断增大,进而使得流体的湍流强度增强,强化了流体之间的换热;(3)水平直管由于受到浮升力的作用,主流区高温流体向上偏移,强化了换热,而水平螺旋管受到了浮升力和离心力的共同作用形成二次流,使得主流区高温流体向外侧偏移,进一步强化了换热。可见,离心力和浮升力是造成强化换热的原因之一。

(a)水平直管

(b)水平螺旋管
2.2 重力对超临界CO2在水平螺旋管内流动的影响
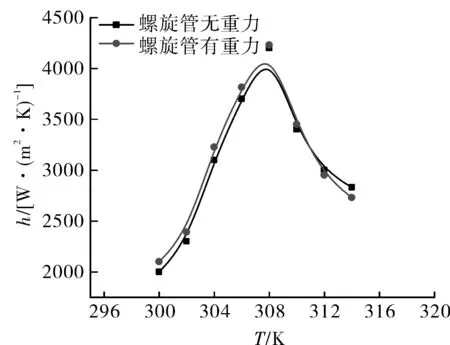
(a)水平螺旋管 (b)水平直管
图6 重力对换热系数的影响对比
重力是流体流动中不可忽视的一个因素,对超临界CO2在管内的换热特性有何影响需要进一步研究。针对水平直管和水平螺旋管,在其他条件相同的情况下,对有无重力进行了数值模拟,得到其随截面流体温度变化的对流换热系数对比图,如图6所示。
从图6(a)可以看出,在螺旋管中,有无重力对超临界CO2对流换热并无太大影响,在各点温度下的对流换热系数基本一致,这是因为重力引起的浮升力相比管结构引起的离心力可以忽略不计,对换热恶化起到了一定的延迟作用。研究证明,浮升力是引起超临界流体在管中换热恶化的主要原因[21]。观察图6(b)可以发现,重力对超临界CO2在直管中的流动是有一定影响的,两种情况下,两者的对流换热系数都在准临界点达到最大值,无重力的换热系数要比有重力的换热系数大14%,而在306~312 K的温度区间,无重力的对流换热系数都比有重力的换热系数要高出很多。这是因为在有重力的情况下,重力引起的浮升力强化了近壁处流体的流动速度,使得流体层流化,降低了湍流度,从而降低了换热能力,而在306~312 K超临界CO2的密度较大,重力引起的浮升力较为明显,换热恶化也就更为严重,重力对直管内的对流换热系数影响也就越大。在其他区间,流体密度较小,浮升力的作用不明显,重力对换热效果的影响并不大。
2.3 管径对超临界CO2在水平螺旋管内流动特性的影响
在相同压力(P=8 MPa)、热流密度(q=30 kW/m2)、质量流速(G=250 kg/m2·s)、进口温度45 ℃的条件下,分别对管径4,6,8 mm的水平螺旋管进行了模拟计算,最终模拟得到沿程温度及换热系数,以探究螺旋管管径对换热性能的影响。
为便于分析,分别绘制了3种不同管径的螺旋管沿程壁面温度变化以及轴向截面温度变化的对比图,如图7所示。图中横坐标为圈数,进口处为0圈,沿程走一节为1圈。
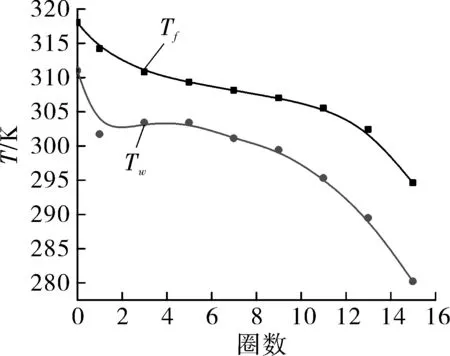
(a)4 mm螺旋管 (b)6 mm螺旋管 (c)8 mm螺旋管
图7 3种不同管径的螺旋管沿程壁面温度变化以及轴向截面温度变化的对比
由图7可以看出,沿管程方向,3种螺旋管的壁面温度和流体温度都有不同程度的下降,同样是318 K的进口流体温度,4 mm螺旋管的出口流体温度为290 K;6 mm螺旋管的出口流体温度为305.8 K;8 mm螺旋管的出口流体温度为307.6 K,可见4 mm螺旋管中的壁面温度和流体温度比另两种螺旋管都有更明显的下降,可知管径对超临界CO2在水平螺旋管中的换热是有影响的。3种螺旋管中的流体温度都在流程的第1圈迅速降至310 K以下,这是因为在管的入口段湍动强烈,换热效率较高。4 mm螺旋管Tw由311 K下降到280.2 K,下降了30.8 K,Tf由318 K下降到290 K,下降了28 K;6 mm螺旋管Tw由311 K下降到297.5 K,下降了13.5 K,Tf由318 K下降到了306.2 K,下降了11.8 K,8 mm螺旋管Tw由310.4 K下降到300.6 K,下降了9.8 K,Tf由318 K下降到307.8 K,下降了10.2 K。可知随着管径的增大,温降在减小,且随着管径的增大,温降减小的程度也越小。
为深入研究不同管径对流动换热的影响,取3种管的相同位置的局部对流换热系数进行比较,局部对流换热系数的对比如图8所示。

图8 不同管径下的换热系数对比
由图8可以看出:(1)对比沿程温度图,不同管径的换热系数峰值点皆出现在准临界温度点附近,这是因为超临界CO2在准临界点附近具有较大的密度和比热容,使得主流区域与壁面产生较大的温度滑移,强化了换热;(2)随着管径的增大,相同截面流体温度对应的换热系数更小,这是因为管径越大,流体所受的浮升力越大,增大的浮升力与流体所受的离心力相抵触,由此形成的二次流变弱,从而使换热系数变小,且整体换热系数依次下降8%;(3)随着管径的增大,局部对流换热系数的峰值对应的坐标位置向右偏移,这是因为在未达到临界点之前,管径较大的管内湍动与小管径相比更弱,换热系数更小,局部温差较小,峰值的到来也就更晚。
2.4 节距对超临界CO2在水平螺旋管内流动特性的影响
为了研究节距对超临界CO2在水平螺旋管内流动换热的影响,分别对节距为10,50,100 mm,管径4 mm的水平螺旋管进行数值模拟。3种螺旋管的沿程截面流体温度及壁面温度如图9所示。

(a)节距10 mm (b)节距50 mm (c)节距100 mm
图9 3种不同节距的螺旋管温度分布
由图9可以看出,沿程截面流体温度与壁面温度的温差都是先变小再变大,这是由于CO2物性随温度的变化而发生改变,进而再影响温度的变化。节距10 mm与节距50 mm螺旋管的温度沿程变化趋势几乎一样,且壁面温度的出口温度和截面流体温度的出口温度是近似一样的,而节距100 mm的螺旋管与以上两种节距不同的螺旋管相比却有较明显的变化。节距10 mm螺旋管Tw由311 K下降到280 K,下降了31 K,Tf由318 K降到294.6 K,下降了23.4 K;节距50 mm螺旋管Tw由311 K下降到 281 K,下降了30 K,Tf由318 K下降到296 K,下降了22 K;节距100 mm螺旋管Tw由311 K下降到292.1 K,下降了18.9 K,Tf由318 K下降到303.4 K,下降了14.6 K。可见在节距较小时,节距的变化并不能引起温度的变化,只有当节距增大到一定程度时才会引起沿程温度的变化,且随着节距的增大,沿程壁面温度和截面流体温度的温降都在变小。
为深入探究节距的不同对水平螺旋管换热的影响,对这3种螺旋管的对流换热系数进行比较,如图10所示。

图10 不同节距下的换热系数对比
由图10可以看出:(1)节距10 mm与节距50 mm螺旋管的对流换热系数相差无几,说明当节距较小时,节距的变化并不能影响对流换热;(2)当节距增大到100 mm时,螺旋管的换热系数有明显下降,说明当节距增大到一定程度时,会随着节距的增大,换热系数降低,这是因为随着节距的增大,弯曲程度有明显减小,流势愈加平缓,流体所受的离心力变小,导致湍流度降低,进而影响换热系数;(3)节距100 mm螺旋管的最大换热系数对应的流体温度要比节距10 mm和50 mm的最大值点对应的温度要小一些,说明节距对超临界CO2对流换热的准临界温度有一定影响。
3 结论
本文利用数值模拟的方法研究了超临界CO2在水平螺旋管内的冷却流动换热特性,并对不同管径和节距的换热管进行了对比分析,主要得到如下结论。
(1)由于超临界CO2的物性随着压力和温度变化剧烈,其在准临界点附近具有较大的密度和比热容,使得主流区域与边界具有较大的温度梯度,强化了换热,进而造成了换热管在准临界点附近具有较大的换热系数。
(2)在保持质量流量、入口压力和热流密度一定的前提下,水平螺旋管相对于水平直管具有更佳的换热性能,对流换热系数高出水平直管15%,离心力和浮升力使得主流体发生偏移、强化了换热,是造成换热系数增大的原因。
(3)重力对超临界CO2在螺旋管中的对流换热特性影响不大,其会对直管中准临界附近区间产生影响,造成换热恶化,降低湍流度,减小换热效率,在准临界点,重力影响达到最大,无重力换热系数比有重力换热系数高14%。
(4)在保证螺旋管的其他结构参数相同的前提下,随着管径增大,离心力与浮升力产生的二次流变弱,其换热系数变小,管径每增大2 mm,螺旋管的整体换热系数下降8%。
(5)模拟结果显示,当节距小于50 mm时,节距的变化并不会对换热产生影响,当节距增大到100 mm时,换热系数有明显下降,可知当节距增加到一定程度时,离心力引起的湍流度降低,二次流减弱,导致管内换热系数减小。

