微结构阵列的超精密偏心加工方法*

林泽钦，王素娟，陈新度

(广东工业大学 机电工程学院 广东省微纳加工技术与装备重点实验室，广州 510000)

0 引言

随着现代光学技术不断朝着微型化、集成化的方向发展，微结构阵列表面被广泛应用于现代光学系统中。超精密加工技术可以实现微结构阵列的加工，如微透镜阵列、正弦波阵列、微金字塔阵列等[1-3]，不需要抛光等后续加工工序，即可达到亚微米级的形状精度和纳米级的表面光洁度。慢刀伺服技术是一项重要的超精密加工技术，通过对机床C轴进行位置控制，利用CXZ轴联动可实现对微结构阵列等非旋转对称曲面的加工[4-5]。然而，慢刀伺服的加工轨迹在工件XOY平面上的投影为绕工件中心的螺旋线，各个微结构单元上的切削轨迹分布并不相同，影响了各单元上误差分布的一致性[6-7]。加工过程中，当刀具经过基面和单元的交接位置时，Z轴会出现较大的加速度而影响加工的稳定性，单元边缘处的表面粗糙度、形貌精度往往会恶化[8-9]。

本文提出一种基于超精密车床四轴联动的偏心车削加工方法，通过机床CXYZ轴联动实现微结构阵列中各个子单元的独立加工，从而提高单元的加工一致性及Z轴加速度的均匀性，并分析了偏心加工方法的加工特点，建立了偏心车削的刀具轨迹生成算法和形貌预测模型。

1 加工系统说明

超精密偏心加工方法可应用于四轴及以上的超精密车床，单点金刚石车刀安装在机床C轴上，工件安装在Z轴平台上，如图1所示。以Moore公司的超精密加工机床350FG为例，机床的C轴为旋转轴，并配备精密转角位置反馈的传感系统，可以实时获取C轴的转动角度。X、Y、Z轴为直线轴，可以配合C轴转角做相应的进给，通过各轴联动加工出微结构阵列。

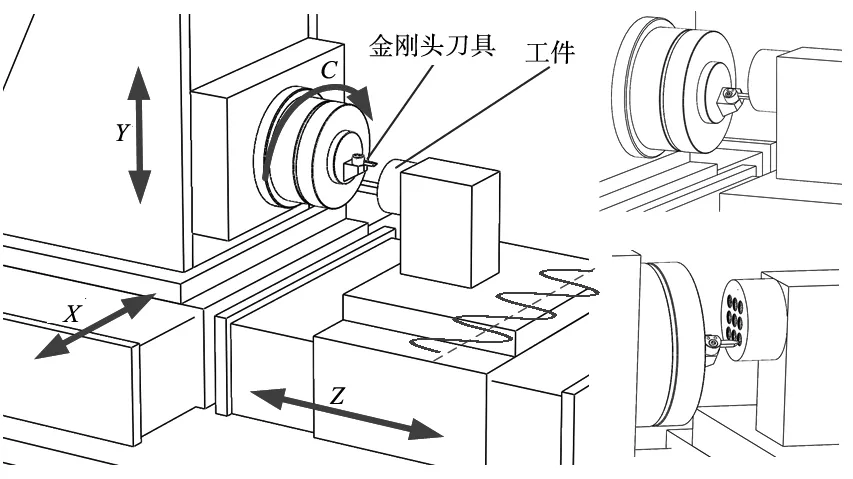
图1 偏心加工系统示意图

加工前，需要完成加工系统的对刀工作。在常规的慢刀伺服车削加工中，可通过试切、测量，获取机床的对刀误差，再调整X、Y轴的位置以减少对刀误差，控制误差在允许误差范围内(一般是1μm以内)。而偏心车削的加工方法，由于刀具安装在C轴上，加工系统仅有刀具角度可以通过机床C轴旋转调节，刀尖与C轴中心的安装误差无法通过机床的运动调整。为此，通过分析偏心加工方法中对刀误差对轨迹生成的影响，结合加工系统的结构提出了相应的对刀方法和轨迹生成方法。

图2 对刀流程

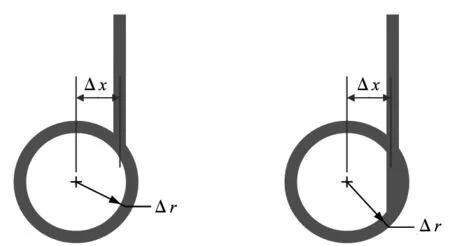
(a) Δy>0,sign为+ (b) Δy<0,sign为-图3 对刀试切形貌

2 刀具轨迹生成算法

针对偏心车削加工方法的加工系统结构形式，考虑对刀误差的影响，可建立加工系统的运动学模型；再结合所加工的微结构阵列的单元几何参数，进行刀具半径补偿，可生成加工轨迹和机床加工代码。

2.1 坐标系建立及变换

对于偏心加工方法应用的机床运动链，根据多体系统理论，釆用低序体阵列描述机床各部件的固联关系，并釆用齐次变换矩阵，可计算刀具切削点相对于工件坐标系的位置坐标，以及刀具相对于工件坐标系的姿态。机床的拓扑结构见图4。

图4 机床的拓扑结构

(1)

(2)

(4)

(5)

(6)

其中，如图5所示，θ0为刀具前刀面水平时C轴角度，Δθ和Δr则是试切对刀时得到的偏置角度和偏置距离。

图5 六边形分布凹球面透镜阵列的偏心加工轨迹图

定义Wp和Wv分别表示工件坐标系下的刀具位置和方向，从机床运动链可知：

(7)

(8)

其中，I3为3阶单位矩阵。

2.2 偏心加工的阵列刀具轨迹生成

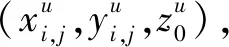
(9)

其中，ρu为点p到该单元中心的距离，θu为点p与单元中心连线和水平方向的夹角。

加工过程中，刀具前刀面应始终垂直于刀具轨迹，即切削运动在刀尖前刀面进行，切屑在前刀面产生。因此，在生成加工轨迹时需要考虑工件坐标系下的刀具方向，对于点p有式(10)：

(10)

综合式(7)～式(10)，可得到机床各轴的运动方程：

(11)

其中，刀具轨迹点的Z坐标值需要根据微结构阵列的几何形貌、刀具尺寸，进行刀尖半径补偿计算得到。以六边形分布的凹球面透镜阵列为例(见图5)，使用偏心加工方法，每个单元的加工轨迹在XOY平面的投影为螺旋线，刀尖的切削面始终与切削方向垂直，而Z轴根据单元的形貌参数，做相应的进给运动。

针对每个单元使用等角度离散的方法计算加工轨迹离散点，将每转的刀具轨迹等分为nθ个点。等角度离散方法的代码计算简单、计算量少，且由于阵列单元尺寸较小，该方法产生的弦长误差较小。假设单元轮廓半径为Ru，每个阵列单元几何参数相同，对每个单元上的刀具点p，有：

(12)

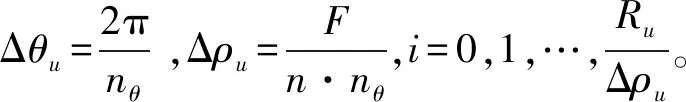
在Z方向上进行刀具半径补偿计算(见图6)，凹球面微透镜阵列单元在刀具补偿后的Z坐标值可表示为：

(13)

综合式(11)～式(13)，可计算出各个加工点的在工件坐标系上的坐标值，获得偏心加工的刀具轨迹及对应机床CXYZ轴的坐标值，生成加工代码。

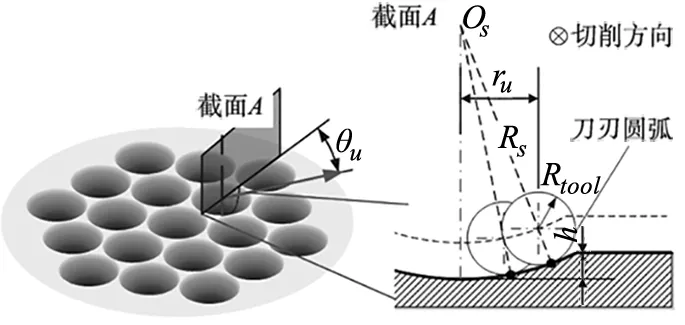
图6 凹球面透镜刀尖半径补偿示意图

3 仿真验证

基于上述理论分析，建立了偏心加工微结构阵列的刀具轨迹生成算法及表面形貌预测模型。为了验证偏心加工方法的特点及优势，对慢刀伺服加工和偏心加工方法进行对比，以六边形排布的凹球面微透镜阵列作为加工对象，进行仿真分析。

对于圆形孔径的微透镜阵列，其阵列单元的排布形式、位置决定了该阵列的填充因子，不少光学应用中都要求微透镜阵列有尽可能高的填充因子[10]。而六边形阵列是一种常用的分布形式，其填充因子最高可达90.7%，此时透镜单元边缘相切，这对单元边界的加工要求高，需要避免加工出现单元交叠的现象。

3.1 仿真计算

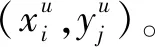
表1 仿真参数

3.2 刀具轨迹生成及形貌预测

使用Matlab软件，根据表1的仿真参数，分别计算慢刀伺服加工方法和偏心加工方法的加工刀具轨迹，并预测加工后的表面形貌。从图7可见，对于传统慢刀伺服加工方法，每个单元上的刀具轨迹与单元的分布位置相关，也决定了加工表面的刀痕分布。而偏心加工方法实现了每个阵列子单元的独立加工，单元之间的刀具轨迹及表面形貌具有很高的一致性。

(a) 慢刀伺服加工

(b) 偏心加工 图7 不同加工方式下刀具轨迹与透镜单元形貌预测

(a) 慢刀伺服加工 (b) 偏心加工

(c) 慢刀伺服加工 (d) 偏心加工

(e) 慢刀伺服加工 (f) 偏心加工 图8 不同加工方式下Z轴位移、速度及加速度曲线

3.3 加工系统动态性能

分析加工过程中Z轴运动的坐标值，可计算Z轴的速度和加速度，如图8所示。从图8a、图8c、图8e中可见，使用传统的慢刀伺服加工方法，由于C轴转速恒定，刀具在经过透镜单元的边界区域时，Z轴会出现较大的加速度。这不利于系统的稳定，容易造成边缘加工质量的恶化。为此，有学者提出面形延拓的方式，可将加工轨迹中加速度大的切削点设定到工件之外，以避免其对工件表面的影响[9-11]，然而当阵列设计填充因子大、各个子单元间距小甚至交叠的情况，该方法需要配合分区加工才能实现。

使用偏心加工的方法，刀具在进入和离开阵列子单元时，其运动不受C轴转速的限制，因此，可灵活设定Z轴的加减速曲线。如图8b、图8d、图8f所示，在刀具进入和离开子单元时，此处使用了二次方程插值得出Z轴移动过程中的坐标点，在进入和离开子单元时减小加速度。而加速度大的轨迹则设计在完成一个单元的加工，提刀离开工件表面后的区域，在两个子单元之间的过渡轨迹中出现，从而避免对工件形貌的影响。此外，如图7b可见，该过渡轨迹不受各子单元的间距的限制，可应用于透镜单元轮廓相切甚至交叠的阵列表面。

4 结论

针对微结构阵列的超精密加工需求，提出一种超精密偏心车削加工方法，并基于该方法的机床运动模型、对刀误差等分析，建立了相应的刀具轨迹生成算法和微结构阵列加工形貌预测模型。通过仿真分析，可获得如下结论：

(1) 偏心加工方法有利于提高阵列单元的一致性，并使得单元误差以该单元中心对称分布。

(2) 偏心加工方法可灵活设置单元边界加工的Z轴速度，减小Z轴加速度，提高单元边缘的加工质量。

偏心加工方法的加工形貌特点，也有利于提高微结构阵列的光学应用效果，抑制成像畸变和单元边界恶化导致的杂散光[6]。偏心加工方法受刀具后角限制小，可适用于加工如菲涅尔阵列、微棱镜阵列等慢刀伺服无法实现的单元截面轮廓斜率大的阵列表面，未来将研究该加工方法进行此类零件的加工。