基于Tabu参数辨识的直线电机推力波动复合抑制方法*

林 健，谢高硕，施昕昕，周 磊，王通通，刘 晗

(南京工程学院 先进数控技术江苏省高校重点建设实验室，南京 211167)

0 引言

数控机床中为实现高速度高精度切削通常采用有铁芯永磁同步直线电机(PMSLM)作为驱动元件。有铁芯直线电机在具有高刚性、大推力优势的同时又具有齿槽效应和端部效应。齿槽力和边端力一般合称定位力，定位力随着直线电机动子的位移而呈周期性变化，是导致直线电机推力波动的重要因素。除此以外，负载阻力变化、非线性摩擦力、纹波力、电机参数变化、永磁体磁链谐波扰动等因素也会引起非周期性推力波动。推力波动导致电机震动、噪声，严重影响进给系统的跟踪精度[1-2]，有必要对其进行抑制。

抑制推力波动多从电机本体优化设计与控制策略两个方面进行研究。本体优化设计在消除推力波动上取得了一定成果，但增加了制造难度和生产成本[3-4]。控制策略常用的有神经网络、自适应控制和迭代学习[5-7]，这些方法在有效抑制推力波动的同时运算量增加，算法运行时间较长，影响了控制的实时性。文献[8-9]在控制系统中加入扰动观测器减小推力波动，但对周期性扰动的抑制效果不明显。文献[10-11]提出通过改变q轴电流抑制周期性定位力，但此方法不能抑制摩擦力、电机参数变化、永磁体充磁不均等不确定性因素引起的推力波动。

基于以上分析提出一种基于扰动观测器与定位力前馈控制相结合的复合控制策略。运用禁忌搜索算法辨识定位力数学模型中的幅值和相位参数，并据此设计前馈控制器，以抑制由周期性定位力引起的推力波动，同时设计扰动观测器作为反馈，抑制非周期因素引起的推力波动。

1 PMSLM定位力特性分析

由文献[12-13]可知，PMSLM动子绕组不通电时齿槽力矩由铁芯和永磁体之间作用力切向分量的波动产生。电机运行时，永磁体两侧与对应的电枢齿之间构成的区域磁导变化大，导致磁场储能随之变化，进而产生齿槽力矩。齿槽力矩定义为动子绕组不通电时磁场能量W相对于位置角α的负导数：

(1)

(2)

式中，μ0为磁导率，B(θ,α)为气隙磁密，Br(θ)为定子永磁体剩磁，δ(θ,α)为有效气隙长度，hm(θ)为永磁体充磁方向的长度，V为气隙体积。指定α为某一电枢齿中心线与某一永磁体中心线之间的夹角，即动子与定子的相对位置角，θ=0处即为指定的永磁体中心线位置。

对W中参数进行傅里叶分解，可得：

(3)

(4)

当定子长度为C，初级位移为x，类似于永磁同步旋转电机偏转α=2πx/C角度，此时W对α求导，可得PMSLM齿槽力矩表达式为：

(5)

式中，z为动子槽数，D为直线电机初级外直径，C为定子长度，δ为气隙长度，p为极对数，n为使nz/2p为正整数的正整数。

虽然式(5)由永磁同步旋转电机(PMSM)推导而来，但是PMSLM可视为将PMSM沿径向剖开展成直线，因此可近似认为式(5)即为PMSLM齿槽力矩表达式。

端部力源于动子两端磁场畸变。铁芯每移动一个极距，端部力变化一个周期。动子两侧端部力可表达为：

(6)

(7)

式中，γ=Lk+iτ，Lk为铁心长度，i为任意整数，x表示位移。

则总端部力Fend为：

(8)

(9)

在参数不变的情况下，理论上定位力只与动子在定子上的位置有关，且呈周期性变化。而电机在不同速度下，参数会因实际工况的影响而变化，因此定位力受位置和速度两种因素的影响。由以上分析，定位力可表示为：

(10)

式中，k为正整数，Ai为i次谐波的幅值，ωi为i次谐波的频率，x为动子的位移，Ff为定位力，φi为i次谐波的相位。为准确地抑制定位力，需对定位力模型的参数进行辨识，即可得到定位力与速度、位置之间的定量关系。

2 禁忌搜索算法改进

禁忌搜索算法源自局部邻域搜索算法，与之不同的是加入了模拟人脑的智能来搜索最优解。禁忌搜索算法仿照人脑的记忆建立禁忌表，记录寻优的过程并作为下一步寻优的指导，减少寻优过程盲目性，同时加入特赦准则防止漏掉最优解，在保证收敛性的同时兼顾种群多样性。

为优化算法性能，下面对禁忌搜索算法的要素进行优化，如邻域范围、禁忌长度、特赦准则等。

(1)邻域范围

根据搜索不同阶段的目标动态调整邻域范围。在迭代初期，扩大邻域以保证搜索的全局性，为避免搜索盲目性，在邻域内设置最大搜索次数，当搜索超过最大次数且未找到最优解，则终止搜索并进入下一邻域。而当搜索至最优解附近时，为加快搜索速度缩小邻域范围。

(2)禁忌长度

动态调整禁忌长度l，将其设计为与迭代次数相关的函数。迭代初期，设置l较小，可实现分散搜索，避免陷入局部极小；迭代后期，设置l较大，便于提高收敛速度。

(3)特赦准则

据上文所述，随着迭代次数增加，禁忌长度随之增大，搜索过程中可能发生返回结果不理想而所有候选解均被禁忌的情况，为此做以下改进：若发现比当前最佳状态更优的禁忌对象，则无视其禁忌属性并将其更新为当前最佳状态。

(4)终止准则

一般将是否达到最大迭代数作为终止判据，其缺陷是如果迭代数用尽却未搜索到最优解，则搜索将以失败告终。另一常用判据是最大允许误差小于某一值，但因无法预先得知最优解而导致判据实现困难。对此做如下改进：为整个寻优过程设置若干迭代次数周期，在一个周期内如果最优值有改善则迭代继续，否则迭代终止。

3 定位力参数辨识

将定位力数学模型中的需要辨识的参数Ai、φi以二进制编码，然后组合成一个二进制码串，构成算法寻优的初始解。

适应度函数定义为：

(11)

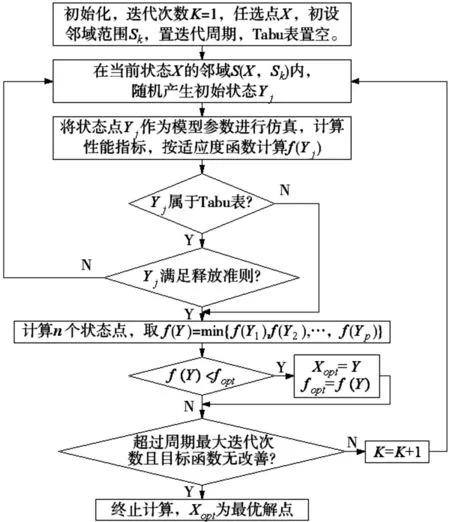
图1 基于Tabu搜索的定位力模型参数辨识流程

当适应度函数小于最小设定值，满足终止准则，则搜索到的最优解即为定位力数学模型的参数。通过实验测得直线电机在不同速度下的定位力数据，运用Tabu算法对模型参数分别进行辨识，得到Ai、φi随速度的变化关系，据此得到不同速度下对应的定位力模型参数，在此基础上设计定位力前馈控制器。

4 扰动观测器设计

扰动观测器可以将摩擦力、纹波推力等不确定性因素造成的扰动视作负载力的变化，并转化为补偿电流加到控制系统中，以抑制内外扰动对推力的影响。采用积分+比例形式的DOB[14]，有更好的辨识收敛性和更快的辨识收敛速度，可有效提高直线伺服系统的跟踪精度。

建立PMSLM运行时的动力学方程：

(12)

式中，Fe为电磁推力；m为动子质量；v为动子速度；b为粘滞摩擦系数；Fd为扰动力；FL为负载力。

PMSLM采用id=0矢量控制，电磁推力可表示为：

(13)

式中，K为推力常数；iq为q轴电流；ψf为磁链。

负载推力Fd的变化在很短的时间内可视作不变即dFd/dt=0。根据式(12)将v、Fd视为状态变量写成状态方程：

(14)

构建状态观测器：

(15)

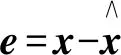
由式(14)、式(15)可得：

(16)

则观测器特征方程为：

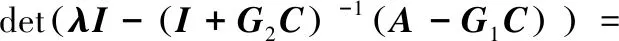
(17)

期望表达式为：

λ2-(p1+p)2λ+p1p2=0

(18)

根据期望极点p1、p2及期望表达式(18)可得：

(19)

设计g11、g21等于0，忽略b，可得状态反馈系数：

(20)

由式(15)可得：

(21)

为抑制测量噪声，在DOB中串联低通滤波器Q(s):

(22)

式中，τ为观测器时间常数。

根据式(13)、式(21)构造扰动观测器如图2所示。

此DOB以电机运行速度v与电机q轴电流分量iq作为输入，当受外界扰动时，可将观测到的扰动以电流的方式等价补偿到电机的q轴电流中。

综上所述，基于扰动观测器与定位力前馈控制的推力波动复合控制系统如图3所示。

图3中，icom为扰动观测器补偿电流，Ke为反电动势常数，ipre为前馈控制器补偿电流。L表示定子电感，R表示定子电阻，Gx(s)为位置控制器、Gv(s)为速度控制器、Gi(s)为电流控制器。

图2 扰动观测器结构图

此控制系统采用三闭环结构。最外环为位置环，中间为速度环，内环为电流环，前馈控制器根据期望速度输出的前馈补偿电流ipre、扰动观测器输出的扰动补偿电流icom与期望电流iq*三者叠加，并与实际的q轴电流比较，误差作为电流控制器输入，对推力波动可以起到综合补偿作用。

图3 PMSLM复合控制系统框图

5 实验验证

实验使用Kollmergen公司的永磁同步直线电机，使用德国HEIDEHAIN公司生产的LIDA485型直线光栅尺，测量长度1840mm。观测器时间常数τ取0.001。整个永磁同步直驱电机实验系统平台如图4所示。电机主要参数如表1所示。

图4 直线伺服系统实验台

实验以电机运行在50mm/s为例，用往复运动双向测试法测量样机在50mm/s速度下的定位力，测得定位力曲线如图5所示。将得到的定位力数据进行FFT变换，得到其包含的主要谐波分量，并针对主要的谐波分量进行补偿。

表1 直线电机参数

幅频特性曲线如图6所示，图6中有5个较高的峰值，基频ω1=0.0104Hz，后4个频率分量分别为基频的2倍、3倍、5倍和6倍。则推力波动表达式为：

Ff=∑Aisin(2πωix+φi) ，i=1,2,3,5,6

(23)

利用禁忌搜索算法辨识出模型中的Ai，φi，辨识的结果为A1=1.12、A2=1.145、A3=3.52、A5=1.23、A6=7.38，φ1=-1.03、φ2=1.42、φ3=1.39、φ5=-0.85、φ6=-0.65。将辨识出的参数带入式(23)中并进行拟合，将拟合得到的曲线与实测定位力曲线比较，如图5中所示，可以看出，拟合曲线基本符合实际曲线，能达到对定位力进行补偿的目的。

分别测量电机运行在50mm/s时原系统、加入前馈补偿、加入前馈补偿和DOB后的q轴电流与跟踪误差。结果如图7～图9所示。未加任何补偿时，q轴电流调节幅度较小，电机的稳态跟踪误差最大值约32μm，且跟踪误差呈现明显的周期性特征；加入前馈控制器对定位力进行抑制后，q轴电流调节幅度有一定程度的提升，电机稳态跟踪误差最大值降为17μm左右，周期性误差得到有效的抑制，但跟踪误差幅值依然较大；当控制系统同时加入前馈补偿器和DOB后，q轴电流调节幅度增大，跟踪误差最大值进一步下降，约为5μm，系统跟踪精度明显提高，反映了复合控制方法对推力波动的抑制效果。

为测试在100mm/s运行速度下复合控制策略对推力波动的抑制效果，用同样的方法对直线电机的定位力进行测量与参数辨识，并分别测量电机运行在该速度时原系统、加入前馈补偿、加入前馈补偿和DOB后的跟踪误差，结果如图10～图12所示。未加任何控制时，电机的稳态跟踪误差最大值约为36μm，加入前馈控制器对定位力进行抑制后，电机稳态跟踪误差最大值降为18μm左右，再加入DOB后，跟踪误差最大值进一步下降约为6μm。

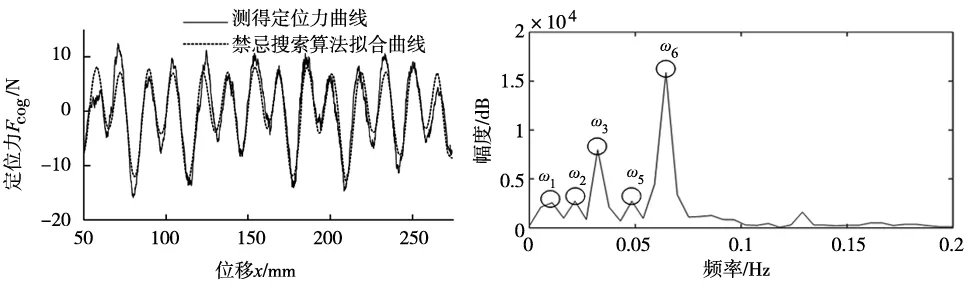
图5 定位力曲线 图6 定位力曲线频谱

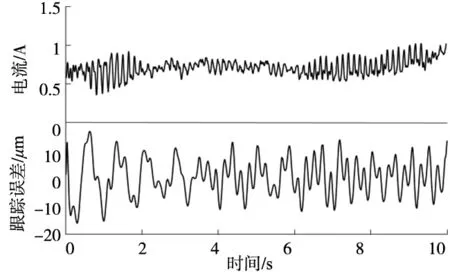
图7 原始系统q轴电流与跟踪误差(V=50mm/s)

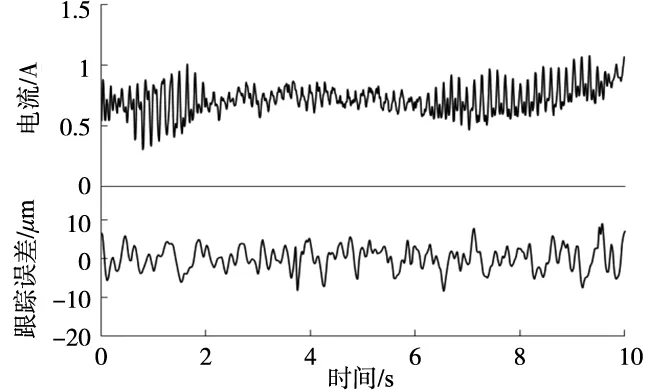
图8 加入前馈补偿后q轴电流与跟踪误差(V=50mm/s)

图9 加入前馈补偿与DOB后q轴电流与跟踪误差(V=50mm/s)

图10 原始系统跟踪误差(V=100mm/s)

图11 加入前馈补偿后跟踪误差(V=100mm/s)

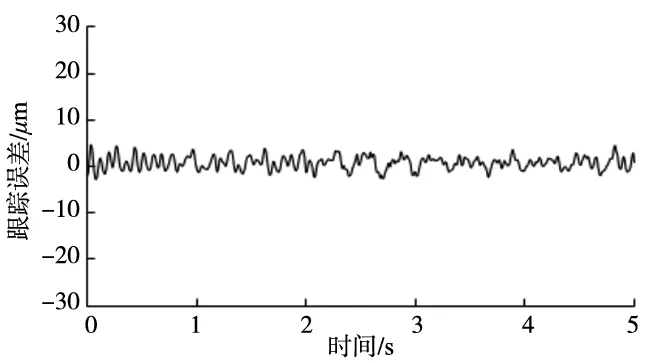
图12 加入前馈补偿与DOB后跟踪误差(V=100mm/s)

6 结论

为抑制直线电机的推力波动，分析定位力周期特性，将改进的Tabu算法用于辨识定位力模型参数，以此为基础设计前馈控制器，同时设计新型DOB以抑制非周期扰动。主要结论如下：

(1)对Tabu算法的邻域范围、禁忌长度、特赦准则、终止准则进行了改进，保证了初始解的全局性，避免陷入局部最优，同时提高了算法的后期收敛速度和参数辨识精度。运用改进的Tabu算法辨识定位力模型参数并搭建前馈补偿器，定位力补偿更精确，有效抑制了周期性推力波动引起的跟踪误差。

(2)单纯应用DOB或定位力前馈补偿，对多种因素引起的推力波动无法做到全面抑制。将二者有效结合，一方面对周期性推力波动采用定位力前馈补偿，另一方面对非周期性推力波动采用积分+比例形式的DOB进行抑制，跟踪精度明显提高，复合控制策略达到了预期的效果。