电网断面越限预测滑动可变窗口方法研究
张 锐,赵瑞锋,王海柱,郭文鑫
(广东电网有限责任公司电力调度控制中心,广东 广州 510600)
0 引言
稳定断面作为电网重要组成部分,其安全稳定与否对电力系统的安全运行有直接影响,需要电网运行人员予以重点监视和控制。依靠稳定断面分析来快速识别系统中的重要输电断面,研究电力系统的薄弱环节,对保证电网的安全可靠运行、防止大面积连锁性故障的发生具有重要意义。目前,随着电力系统自动化技术的发展,开展对海量存储的断面历史状态数据分析,统计用户自由定制组成的设备稳定断面的历史过载信息,进行稳定断面越限预测分析,供调度和方式进行稳定断面预警,具有重要的理论和实践意义。
现阶段,已有很多方法可用稳定断面越限分析,如回归分析模型、时序分析模型、灰色模型(grey model,GM)[1-3]等,但大部分模型都有一定的局限性。回归分析模型对样本容量要求较高,观测数据过少会严重影响试验结果[4-8],时序分析模型在模型适应性、时序的间距等方面仍需进一步探索[7-10],GM在发生突变时预测精度极低[9]。针对现有模型过于复杂及效率过低的问题,本文提出了滑动可变窗口方法,对数据进行回归分析,简化对电网稳定断面越限的分析预测。
1 预备知识
本系统使用二次多项式回归模型和指数回归模型,对电网稳定断面越限进行动态预测。涉及的理论背景将在下文进行介绍。
1.1 基础回归理论
回归分析是一种统计学数据分析方法,主要目的是了解两个或多个变量之间是否相关、相关方向与强度,同时建立数学模型以实现对数据的最优拟合[11-14]。
回归分析主要分为两类:线性回归分析和非线性回归分析。线性回归给定的样本需要满足线性关系的前提条件,公式如下:
y=β0+β1x1+β2x2+…+βixi+ε
(1)
即:
y=Xβ+ε
(2)
为了对β进行估计,需要借助一种合适的评判标准来寻找β的最优估计。最小二乘法提供了一个标准,其基本原理是使样本数据的均方误差达到最小,成本函数为:
(3)
式中:k为样本的个数。
其向量形式可以表示为:
β=(XTX)-1XTy
(4)
此方法需要满足X列向量线性无关。
本文使用二次多项式回归模型和指数回归模型。多项式回归是线性回归的推广,其公式为:
y=β0+β1x+β2x2+ε
(5)
令x1=x、x2=x2,二次多项式可以转换为二元线性回归,并且在参数估计上并不改变β值。
指数在数学中代表次方,即有理数乘方的一种运算形式。指数回归的普遍公式为:
(6)
式中:α为指数回归系数;β1、β2为指数偏回归系数。本文中只有一个自变量,仅需要用到一元指数回归,其公式为:
y=αβx
(7)
1.2 渐进抽样回归
时序数据的回归分析,应该考虑到样本数据的即时性。显然,对于很多工程预测,如果采用的样本与所需预测的目标点相隔较久,预测结果与实际值会相差比较大,这种情况在进行短期预测时极为明显。
在时间上呈现出一种连续的顺序的数据集,具有时序性。渐近抽样回归考虑了数据的时序特性,以便采集更好的样本。渐近抽样可以动态获取时序样本,如果时序样本量过小,不能很好地反映总体情况,则逐渐增大样本量以对其进行优化,使最终所获取的样本能够最大程度地反映总体特征。
渐近抽样回归是渐近抽样在回归中的应用,其数学描述如下。已知时序数据集为:
D={(xi,yi)|i=1,2,…,n}
(8)
式中:x为自变量;y为响应变量。
渐近抽样拟合是先从数据集D中抽取一个时间上距离元素m最近的子集来预测,然后逐步增加样本量,从而找到一个最优的样本集合以获取对响应变量ym的最优估计。此时的样本量也就是最优样本量。
S={(Xm-iym-i)|i=k,k-1,…,1}
(9)
S*={(Xm-i,ym-i)|i=k,k-1,…,1}
(10)
2 基于滑动可变窗口的动态数据拟合方法
2.1 算法描述
为了保证电网断面运行安全,需要对运行数据进行分析预测,由于电网断面数据量大,传统的数据分析算法难以高效准确地进行预测,本文提出了基于滑动可变窗口的动态数据拟合方法。使用二次多项式模型和指数模型动态预测短时间内电网断面越限次数,以更高效、准确地对电网断面运行状况进行有效判断并采取相应措施。
基于可变滑动窗口的动态数据拟合法是一种新型的动态预测方法。滑动窗口机制中,发送方根据确认信息,可以改变窗口的尺寸,对窗口的大小进行调节以控制流量。将滑动窗口和回归分析相结合,回归分析模型对数据量要求较大的特点,与稳定断面监测数据量大的特点相契合,非常适用于电网稳定断面越限的预测分析。可变滑动窗口方法综合两种方法的优势,灵活取样,针对不同的样本数据,调整合适的样本容量。样本容量即为所谓的窗口,由于预测点是不断变化的,所以可以看作是可变滑动窗口。
本算法实现动态选择样本容量,由于某个特定的样本容量很难适应所有的预测点,所以静态样本容量准确性很低。稳定断面每天都需要监测,获取的数据量极大,对每个预测点都要选取合适的样本容量才能进行准确预测。样本容量过小或过大会导致欠拟合或过拟合,严重影响预测的准确性。所以,为了保证预测的准确性,根据样本数据的不同,所选取的样本容量也应该随之改变。本算法针对不同的预测点,动态获取窗口大小,在每次预测时,程序都能自动获取合适的窗口大小及位置,对数据进行预测,并在预测结束后自动对下一个数据进行预测。在这里不需要人工干预,实现了算法的自动化,减少了人工操作失误对预测准确性的影响,大大提高了预测结果的准确性。

图1 算法流程图Fig.1 Algorithm flowchart
2.2 算法实现
2.2.1 样本容量的动态选取
综合二次多项式模型和指数模型这两种候选模型,确定样本容量下限为4。根据上文介绍,二次多项式拟合有β0、β1、β2三个系数,所以样本量至少为3。但是在样本容量为3时,会出现完全拟合的情况。此时,对其他数据进行预测,很难得到预期的结果。因此,只有在样本中非空数据的个数≥4的条件下,才能进行二次多项式模型拟合和指数模型拟合。选择窗口下限为4,满足了最低样本容量要求。
通过多次迭代提高拟合的准确性,计算样本均方误差。在样本均方误差达到收敛时,确定此时的最小样本均方误差。此次迭代的样本容量即为最优样本容量。
2.2.2 模型的动态选取
本算法涵盖两种模型,分别是二次多项式模型和指数模型。本文主要研究的是电网稳定断面越限次数的变化,曲线走势与二次多项式以及指数函数曲线走势相似,故使用二次多项式拟合和指数拟合比较合适。
导入数据后,进行多次迭代计算,每次均选取一定的样本数据进行二次多项式拟合和指数拟合,得到样本均方误差。在进行一次计算时,可以得到在当前样本容量下两种模型拟合的样本均方误差,选取较小值为此时的最小均方误差,相应的模型即为此时的最优模型。多次计算后,得到最优样本容量时,对应的模型即为最终选取的最优模型。
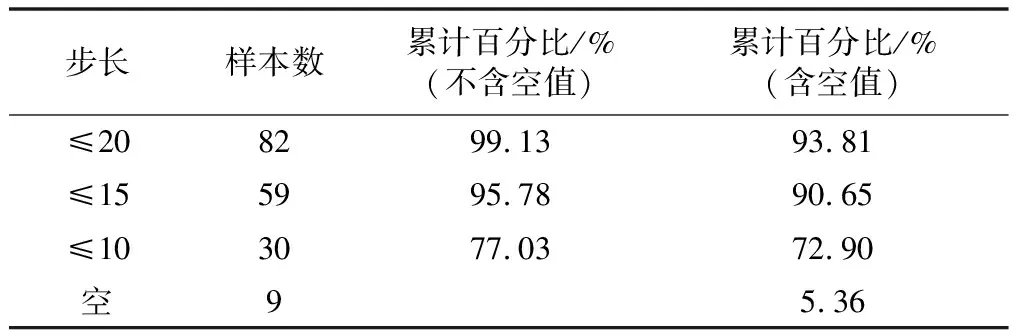
if(abs(e_rmse) { good_model<--"指数模型" chk_err<-- e_err_g chk_yh<-- eyh_g select_rmse<-- e_rmse; select_step<-- es_g } else if(abs(e_rmse) > abs(p2_rmse)) { good_model<--"二次多项式模型" chk_err<-- p2_err_g chk_yh<-- p2yh_g select_rmse<—— p2_rmse select_step<-- p2s_g } 2.2.3 评判标准的确定 本算法选取最小均方误差值(root mean square error,RMSE)为评判标准,对二次多项式模型和指数模型的预测准确度进行比较,选取最优模型。RMSE的计算公式为: (12) 绝对误差是预测值与实测值的差的绝对值,与样本均方误差一样,均能反映预测结果的好坏,但以最小绝对误差作为最优方法的衡量指标,容易出现“过拟合”现象。同时,选择样本均方误差作为标准满足大数定律,其假设随机误差项满足“零均值”和“同方差”的正态分布假设,即ε~N(0,σ2)。所以与最小绝对误差相比较,样本均方误差值更适合作为模型拟合的衡量指标。 2.2.4 收敛性 在实际生活中,之前的稳定断面越限数据,对后续数据的影响微乎其微,所以在预测时样本量不宜过大。为了控制样本量的大小,本算法对迭代次数加以限制。 算法对均方误差进行观测,当均方误差逐渐收敛时,停止迭代。在样本容量递增的过程中,如果样本均方误差有所减小,则继续迭代寻找最优均方误差;如果样本均方误差在7次迭代中都没有减小,可认为均方误差已经收敛,不再扩大样本量,选取最优模型,跳出迭代。 if (p2fg.rmse < p2_rmse) { p2yh_g<--p2yh p2_err_<--p2_err p2s_g<--step p2_rmse<--p2fg.rmse p2_cnt<--0 } else p2_cnt<--p2_cnt+1 本算法根据伯努利试验控制迭代的次数。将样本容量增加1来求解局部最优看成是一次伯努利试验,每次试验可认为是相互独立的(每次都有可能达到最优)。每次试验中结果能否达到最优的概率均为0.5,如果经过连续7次试验都不能改善样本均方误差,7次以后再次改善样本均方误差值的概率小于0.003 91。在给定显著性水平为0.01时,7次试验以后再次改善样本均方误差这一事件为小概率事件,在一次试验中往往不会发生,此时认为在置信度为99%的情况下模型取到最优。此评判标准的添加,有效避免了过拟合的发生,同时让拟合的效果达到最优。 本试验的测试平台及参数为:Intel酷睿i5、8G内存、Windows7,使用Matlab软件进行结果仿真。 本试验基于前文所介绍的预测算法,选取某稳定断面2015年1月至2017年6月的越限数据进行预测,利用Matlab编制可变滑动窗口预测法对所选观测资料进行计算拟合。 拟合所得到的样本均方误差点图和直方图分别如图2、图3所示。直观显示:0.2、0.4、0.6可以作为该测点下的三个阈值标准。 图2 样本均方误差点图Fig.2 Point diagram of sample mean square error 图3 样本均方误差直方图Fig.3 Histogram of sample mean square error 样本均方误差累计分布如表1所示,样本均方误差小于0.4的所占比例达到95%。在所选拟合模型准确性的衡量指标为0.4时,如果某次拟合模型的均方误差大于0.4,表明所确定的动态最优模型在95%的准确率的情况下是不可信的,这时应该予以监控。 表1 样本均方误差累计分布表Tab.1 Cumulative distribution of sample mean square error 为进一步探讨动态最优模型的预测能力,选取所选择样本紧邻的下一次测点数据进行检验,得到校验误差如图4所示。累计分布如表2所示。 图4 校验误差Fig.4 Calibration error 表2 累计分布表Tab.2 Cumulative distribution 根据试验结果得到的最优模型步长的数据分布如图5所示。样本量在15以内所占的比例达到95.78%(如表3),拟合的结果比较理想。样本容量大多数在15以内,超过20的仅为少数,可见样本容量不需要太大,否则只会出现过拟合现象,使预测效果变差。 图5 步长分析Fig.5 Step length analysis 表3 样本步长累计分布表Tab.3 Cumulative distribution of sample step size 电网稳定断面越限预测的研究,在理论和实践上都具有重要意义。本文针对电网稳定断面越限数据特点,提出了一种基于滑动可变窗口的电网稳定断面预测方法。该方法利用二次多项式模型和指数模型,实现了最优拟合模型的动态获取,同时针对不同的模型,动态获取两种模型的最优样本,大幅减小试验误差。在选择最优样本容量时,算法对样本容量进行调整,有效避免了“欠拟合”和“过拟合”现象。试验结果表明,该方法对电网稳定断面越限预测的准确性高。该方法也具有适用性,在应用于其他领域时,根据问题的实际情况,选择相应的模型,也可以达到很好的预测效果。 该方法仍有一些方面需要完善。在数据量特别大的情况下,运行该方法需要耗费大量时间,系统计算成本较高,在以后的研究中,将改进算法的运行速度,使算法更高效、精简。
3 试验与评估






4 结束语

